航天器太陽能電池陣驅動系統激擾因素辨識與擾動機理分析

朱仕堯，雷勇軍，郭 欣

(國防科技大學空天科學學院，長沙 410073)

0 引 言

航天器太陽能電池陣驅動系統(Solar array drive system，SADS)一般由太陽能電池陣和太陽能電池陣驅動裝置(Solar array drive assembly，SADA)兩部分組成。隨著航天任務對航天器性能要求的不斷提升，SADS運轉而產生的持續微幅擾動逐漸成為影響航天器高分辨率對地成像和遠距離激光通信等核心性能的關鍵因素之一。

國內外學者對SADS驅動擾動問題開展了卓有成效的研究。歐空局于1989年在Olympas衛星上進行在軌測量[1]，通過姿態角速度功率譜曲線發現SADS擾動同時包括低頻和高頻擾動成分。文獻[2-4]建立了較為詳細的直接驅動型驅動裝置和太陽能電池陣動力學模型，其中考慮步進電機齒槽效應和負載柔性等因素。Sattar等[5]和Chen等[6]研究了帶有剛性和柔性負載的驅動系統擾動特性問題，其中柔性負載采用集中參數模型模擬，并對步進電機進行線性化處理。Zhou等[7]提出了一種面向驅動控制的間接驅動系統動力學模型，并分析了齒隙和摩擦等齒輪傳動系統非線性因素對電機速度穩定性的影響。Yang等[8]搭建了驅動裝置與小慣量剛性負載系統動力學試驗平臺，并對電磁剛度和阻尼進行試驗測試研究。Li等[9]將慣性負載與驅動裝置之間增加柔性板結構，用于調節一階扭轉振動模態，并研究了擾動力矩頻譜分布規律。程俊波等[10]建立了含永磁同步電機的SADS系統模型，采用模糊控制克服非線性摩擦影響，從而減少電池陣振動擾動。于登云等[11]采用固定界面模態綜合法建立驅動系統模型，并總結了電流噪聲和控制參數選取不當是引起擾動的主要原因。上述研究側重關鍵部件的模型細化，并直接從擾動頻譜特點判定激擾因素，但SADS擾動的分布頻段較廣、激擾因素較多，需要從系統模型出發分析擾動產生的本質原因、主要激擾因素以及其對擾動時頻特性的影響。

本文在SADS擾動特性[12-13]和模態特性分析[14]基礎上，綜合考慮太陽能電池陣、驅動裝置、驅動控制和減速裝置等內部非線性因素及相互耦合作用，建立系統級驅動系統動力學模型，并通過地面試驗驗證其正確性；在此基礎上，利用還原論思想，削減各種影響因素將驅動系統退化為無擾動的平穩運動狀態，解釋擾動產生的必要條件；進一步辨析激起驅動系統擾動的主要激擾因素，并定量分析各種因

素的影響規律，從而說明太陽能電池陣驅動系統的擾動機理問題。

圖1 太陽能電池陣驅動系統組成示意圖

1 太陽能電池陣驅動系統動力學建模

典型太陽能電池陣驅動系統如圖1所示，其中驅動裝置主要包括驅動控制器、步進電機、電刷-滑環組件以及齒輪減速器等部件。建模假設如下：1)航天器本體結構為剛性體，并約束剛體位移和忽略推進劑消耗；2)忽略由驅動控制微處理器“數電-模電”轉換引入的系統誤差;3)忽略步進電機繞組磁滯、磁飽、互感效應等因素，且繞組自感參數不隨轉子位置變化；4)只考慮齒輪減速器在驅動方向的變形和位移；5)在小變形情況下，忽略太陽能電池陣基板和展開鎖定裝置的材料和連接非線性；6)電刷-滑環間摩擦遠大于步進電機軸承摩擦。圖2說明SADS工作流程可分為驅動控制、驅動執行機構以及太陽能電池陣等三部分。

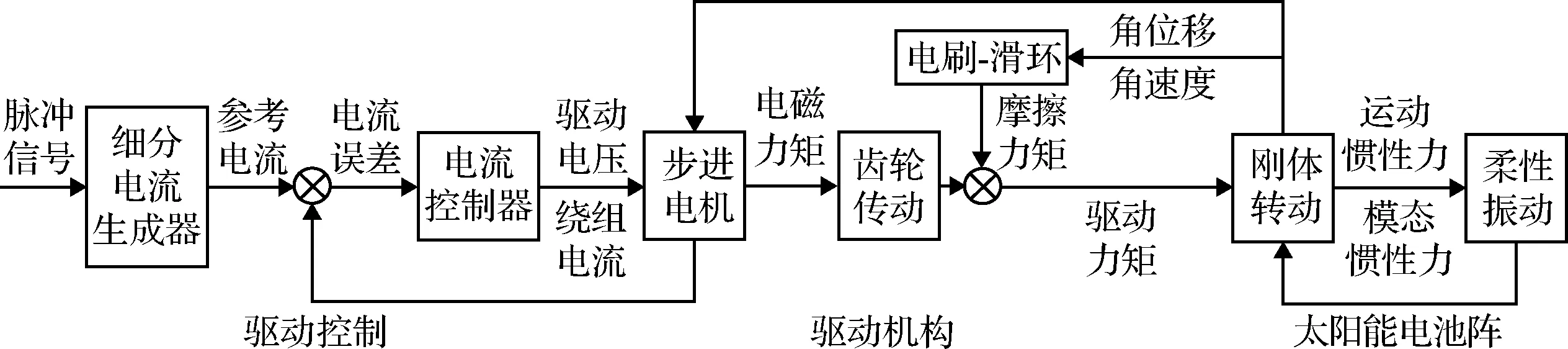
圖2 太陽能電池陣驅動系統典型工作流程

1.1 驅動控制模型

如圖2所示，驅動控制包含參考電流生成器和繞組電流控制器兩部分，分別實現轉速開環控制和電流閉環控制功能。參考電流生成器根據脈沖驅動信號生成細分參考電流；繞組電流控制器將參考電流和繞組電流[15-16]的誤差作為反饋，利用PI控制律調整電機繞組中驅動電壓，保證繞組電流隨參考電流變化：

(1)

(2)

(3)

1.2 驅動機構模型

如圖2所示，在驅動電壓作用下，驅動執行機構根據太陽能電池陣實際轉角偏差調整驅動力矩。對于含有內嚙合直齒輪減速傳動機構的間接驅動型驅動裝置，小齒輪對應步進電機驅動主動軸，其轉速為步進電機的轉速；大齒輪對應太陽能電池陣從動軸，其轉速為太陽能電池陣的轉速，如圖3所示。

主動軸在電機力矩、嚙合力矩以及電機轉子慣性力矩作用下達到平衡：

(4)

式中：rb為小齒輪基圓半徑；Jm為電機轉子軸轉動慣量；Te為定轉子之間的電機力矩；Fg為齒輪傳動力。對于兩項混合式步進電機，可根據虛功原理得到電機力矩[14]：

(5)

式中：Kf為電磁力矩截斷階數；Nb為驅動拍數；Lmk和Lfk分別為定子繞組和虛擬轉子繞組第k階電感系數；前兩項是由定子繞組和轉子永磁體作用產生的電磁力矩，第三項是由定轉子輪齒相互作用引入的齒槽力矩，其中含有驅動倍頻成分。

圖3 齒輪傳動部件傳動關系

此外，齒輪之間的動態嚙合力與輪齒間相互配合密切相關，可以采用圖3所示的嚙合彈性力和阻尼力表征齒面間的動態傳動力Fg(t)：

(6)

式中：kg(t)為時變嚙合剛度，其傅里葉級數展開為：

kg(2k)sin(kNtθm)]

(7)

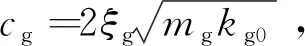
(8)

其中,Δg為靜態傳動誤差，其可以表示為[17]：

Δg(t)=rbθm-rfθa+e(t)=rbθm-

(9)

式中：θa為太陽能電池陣轉角，rf為大齒輪基圓半徑，e(t)為靜態傳動誤差，ek為靜態傳動誤差的諧波項幅值，Nt為小齒輪齒數。

從動軸在驅動力矩Ta、摩擦力矩Tf和齒輪傳動力矩作用下達到平衡，其中從動齒軸摩擦力矩[18]主要由電刷-滑環組件提供：

Fgrf-Ta=Tf=σaωa+[Tc+(Ts-

Tc)exp(-ωa/ωs)]sgn(ωa)

(10)

式中：rf為從動軸轉動慣量，σa為黏性摩擦系數，ωa為太陽能電池陣轉速，Tc為庫倫摩擦力矩，Ts為最大靜摩擦力矩，ωs為stribeck臨界轉速。

1.3 太陽能電池陣模型

如圖2所示，太陽能電池陣在驅動力矩作用下首先發生剛體轉動，由此產生運動慣性力會激起結構柔性振動，并且振動引起的模態慣性力又會反向影響附件的剛體轉動規律。根據虛功原理可以得到太陽能電池陣結構剛柔耦合振動微分方程[14]：

(11)

式中：Ha為模態角動量矩陣H的第二行向量，Ja為轉動慣量矩陣J的第二個對角元，Ta為力矩向量T的第二個元素，η為太陽能電池陣模態坐標。

太陽能電池陣在三個平動和兩個轉動方向的廣義約束力向量(即拉格朗日乘子向量λ)可以表示為：

(12)

式中：S和P為電池陣的靜矩和模態動量矩陣。

1.4 系統模型組集

將式(10)中的驅動力矩Ta代入式(11)，并與式(4)中的主動軸平衡方程聯立得到SADS動力學方程：

(13)

1.5 試驗驗證

1.5.1擾振特性試驗

如圖4所示，試驗對象由驅動裝置(相關參數見文獻[14])、太陽能電池陣模擬件及相關連接件組成。由于太陽能電池陣為多鉸鏈連接結構，且持續轉動，難以進行吊裝，因此設計兩塊構型相同(尺寸為163 mm×400 mm×5 mm)的金屬薄板模擬其在驅動方向的質量和剛度特征，使模擬件滿足轉動慣量(18 kg·m2)和頻率(固支基頻0.8 Hz)等效原則。在模擬件軸線方向配置吊裝組件卸載重力，以減小結構重量對驅動裝置軸承壓力，使其更接近在軌狀態。受限于結構件尺寸較大，試驗室尚不具備模擬高真空和溫度梯度等空間環境的能力。測試系統由Kistler測力平臺、Polytec激光測振儀、信號放大器、數據采集器、計算機和驅動裝置控制器以及試驗數據分析軟件等組成，如圖4所示。測力平臺與驅動裝置固定連接，用于測量驅動方向擾動力矩分量。將激光測振儀測點設置在太陽能電池陣剛性轉接工裝上，在低轉速和忽略工裝彈性變形前提上，可通過測點線速度比例換算得到電池陣實際轉速。測量數據分別經過信號放大器和測振儀后置端進行處理，并利用數據采集器傳遞給計算機；外置驅動器用于產生驅動裝置所需驅動信號，控制太陽能電池陣轉動和停止。

圖4 驅動系統擾動特性測試系統

圖5 穩態擾動力矩分析結果與試驗測試數據

1.5.2試驗結果分析

選取驅動系統轉速穩定后的擾動力矩響應，經過消除趨勢項等數據預處理后得到離散時域數據，并利用傅立葉變換獲取對應的頻域數據。通過調整步進電機的電磁力矩系數修正驅動系統一階固有頻率，使其更接近試驗測試數據；并利用頻譜分布特點，在系統模型中設定第1，3，16，17和18階電磁力矩成分，并對力矩幅值優選得到取值分別為0.054 N·m，0.054 N·m，0.027 N·m，0.027 N·m和0.027 N·m。擾動力矩分析結果與試驗數據如圖5所示，其中穩態擾動力矩時間歷程和頻譜分布曲線與試驗結果非常接近，相對誤差小于10%，如表1所示。綜上，所建立的系統動力學模型可以較為準確地預估驅動系統的穩態擾動規律。

表1 理論分析和試驗測試結果對比Table 1 Comparison of disturbance characteristics between analysis results and experiment data

2 驅動系統激擾因素辨析

在驅動方向上，驅動系統對航天器本體的擾動力矩等于太陽能電池陣驅動力矩的反作用力；在非驅動方向上，廣義擾動力等于航天器本體對驅動系統的約束力。根據力矩平衡方程式(11)和廣義約束力表達式(12)，得到驅動系統對航天器本體的廣義干擾TD：

(14)

圖6 平穩運動假設條件下的驅動系統響應時間歷程曲線

3 激擾因素的擾動特性分析

本部分通過構建單一激擾因素作用環境，逐一分析各激擾因素的擾動特性。在對線性因素分析時會引入系統固有頻率予以輔助，以某型衛星太陽帆板結構為例，其質量39.4 kg，繞驅動軸線轉動慣量為21.5 kg·m2，固支狀態下一階扭轉頻率為1.813 Hz；與直接驅動型SADA(驅動力矩為2.1 N·m，電機齒數為300)組成驅動系統后，由于電機轉動方向的電磁剛度影響，系統整體的一階扭轉頻率降為0.796 Hz。

3.1 電流細分激擾特性分析

整步驅動的步進幅度較大，每次步進所激起太陽能電池陣轉角和振動幅度也相對較大，會在一定程度上影響系統運動規律。現代驅動裝置往往應用電流細分技術對步進角度進行細分，但是細分步進仍然會引起系統角加速度的脈沖變化，影響驅動系統的擾動規律。如圖7所示，電流細分引起的擾動力矩變化具有周期性變化規律，每個細分微步均會引起擾動力矩突變，并伴隨出現最大擾動力矩。擾動幅度隨著細分數的增大而逐漸減小，擾動成分主要分布在細分頻率附近，且擾動頻率基頻(即細分頻率)隨細分數增大而正比例放大。

圖7 細分驅動擾動特性分析

3.2 非線性電磁場激擾特性分析

3.2.1齒槽力矩激擾特性分析

步進電機的定子和轉子均為多齒結構，在轉動過程中兩者之間的輪齒相對位置周期性變化，導致齒隙磁通量發生周期波動，引入具有高階諧波成分的齒槽力矩。如圖8(a)所示，齒槽力矩所激起的擾動力矩均為周期變化，但不同幅度的齒槽力矩所激起擾動的變化規律有所不同；隨著齒槽力矩幅值增大，擾動力矩波動幅度逐漸放大，并且多頻疊加振動效果更加明顯；如圖8(b)所示，擾動成分主要分布在前幾階激擾頻率處；如圖8(c)所示，在所有齒槽激擾階次工況對比中，擾動力矩幅度均隨激擾幅值增大而增大，但明顯呈現非線性對應關系；當激擾頻率或倍頻與系統扭轉模態固有頻率接近時，擾動幅度明顯增大。

圖8 齒槽力矩擾動特性分析

3.2.2高階電磁力矩激擾特性分析

在Δθm取值較小，且較為穩定時，電磁力矩一階分量可以近似認為是角度誤差的比例控制環節，保證驅動負載按照指定的驅動規律運動：

Te1=Lm1ImNmifsin(NmΔθm)≈Lm1ImNmifNmΔθm

(15)

然而，步進電機在生成一階電磁力矩的同時也會產生高階電磁激擾力矩分量。高階電磁力矩表現為隨角位移變化的正弦函數關系：

Tek=kLmkImNmifsin(kNmθm-Nmθm+NmΔθm)

(16)

如圖9(a)所示，電磁激擾作用下所產生的穩態擾動力矩均呈現周期性變化特點；當激擾階次較低時，所激起的結構模態振動響應較小，單頻振動特點明顯；當激擾階次增大至五階之后，擾動力矩表現為多種頻率波動的疊加；如圖9(b)所示，擾動成分集中在電磁激擾頻率及其倍頻附近，并且頻譜峰的取值和數量均隨著激擾階次的提高而逐漸增大或增多；當激擾頻率的高倍頻與系統一階扭轉頻率較為接近時，其頻率分布幅值會明顯增大，例如：六階激擾時的激擾頻率與系統一階扭轉頻率接近，其對應的頻譜峰值可能會超過激擾頻率。在所研究范圍內，擾動幅度均隨著激擾階次和幅度的提高而逐漸升高，如圖9(c)所示。

圖9 高階電磁力矩擾動特性分析

3.3 齒輪傳動激擾特性分析

3.3.1齒輪嚙合剛度和阻尼的激擾特性分析

與直接驅動不同，間接驅動型驅動裝置內部包含齒輪減速環節。在齒輪嚙合過程中，輪齒嚙合剛度和嚙合誤差會隨著輪齒間相對位置改變而周期性變化，所以嚙合剛度和嚙合誤差會引起系統剛度或運動位移的波動，導致驅動系統發生參數自激振動，引起不平穩運動并產生系統擾動。

考慮一階嚙合剛度和嚙合誤差變化情況下的穩態擾動力矩如圖10(a)和圖10(b)所示，其中k0和e0分別為2×106N/m和0.01°，且k1/k0=e1/e0=0.1。嚙合剛度引起的穩態擾動力矩具有周期變化特點，每個周期內的擾動力矩具有嚙合頻率及其倍頻兩種波動頻率；類似地，嚙合誤差所引起的穩態擾動力矩同樣具有周期變化特點，但每個周期內部的擾動力矩僅包含齒輪嚙合頻率一個主要波動頻率。如圖10(c)所示，在所研究的參數范圍內，擾動力矩幅值均隨嚙合剛度和嚙合誤差的時變分量與恒定分量的比值(即k1/k0和e1/e0)的提高而逐漸顯著增大。

圖10 時變嚙合參數擾動特性分析

3.3.2齒輪嚙合間隙的激擾特性分析

齒輪主動輪齒和被動輪齒之間的配合間隙是引起齒輪傳動非線性的重要因素之一。圖11(a)給出了只包含齒側間隙因素情況下的系統響應時間歷程曲線，其中齒側間隙為0.001 m。不難發現在起動階段，主動輪齒和被動輪齒之間的相對位移迅速達到間隙上限(即發生齒側碰撞)，并在0.8 s附近分離后又發生二次碰撞，導致擾動力矩迅速增大；在系統阻尼作用下，擾動力矩逐漸衰減，輪齒間相對位移始終保持在間隙上限，穩態擾動力矩逐漸趨近于零，說明齒側間隙因素只會改變起動階段的擾動特性，不是引起系統穩態擾動的直接因素。

然而，齒槽間隙仍然是影響系統擾動特性的重要因素。如圖11(b)和圖11(c)所示，當齒側間隙為0.002 mm時，一階齒槽激擾幅度變化會導致系統響應規律明顯改變：1)激擾幅度為0.2 N·m時，主動和被動輪齒之間的相位位移始終為間隙上限，沒有出現嚙合面分離現象，擾動力矩連續穩定變化，并呈現單頻率周期波動變化特點。2)激擾幅度增大至0.4 N·m后，主動和被動輪齒之間的相位位移大部分時間內處于間隙上限，但在特定時間節點位置出現周期性的瞬時減小并迅速恢復，即出現齒側分離和碰撞；此時擾動力矩仍呈現周期性波動特點，但在齒側再次碰撞時會明顯提高。3)激擾幅度進一步增大至0.6 N·m，主動和被動輪齒之間的相位位移在間隙上限和下限間周期變化，即主動輪齒與前一被動輪齒分離，并與后一被動輪齒發生碰撞；當主動輪齒與被動輪齒再次配合時，擾動力矩會瞬時增大，然后迅速減小，擾動幅度明顯大于前兩種情況。

圖11 考慮齒側間隙情況下的驅動系統響應時間歷程曲線

4 結 論

針對太陽能電池陣驅動系統擾振機理問題，本研究分析了誘發擾動的前提條件、系統主要激擾因素以及各類激擾的時頻域特點，對航天器驅動系統振動抑制具有重要的參考價值。主要結論如下：

1)所建驅動系統動力學模型考慮了內部耦合關系、非線性因素以及參數時變特性，并通過地面試驗驗證了模型正確性。

2)轉動角加速度和振動加速度不同時為零是引起驅動系統擾動的前提條件；電流細分、齒槽效應、高階電磁力矩分量、齒輪嚙合狀態時變等因素為驅動系統的主要內部激擾因素。

3)激擾因素激起的擾動力矩一般均具有周期性；擾動成分集中在激擾頻率及其高倍頻附近；擾動幅度隨電流細分數增大而減小，隨齒槽激擾幅度、電磁激擾幅度和嚙合參數變化幅度增大而明顯提高。