硬化水泥漿體氣體滲透特征研究

宋 楊，李金遠，李俊鋒，陳 望，吳海洋

(常州工學院土木建筑工程學院，常州 213032)

0 引 言

目前，水泥基材料滲透率研究主要專注于不同條件下的滲透率測試及其影響因素分析。然而，僅通過滲透率測試較難對水泥基材料的孔隙流動特征進行分析，更難理解其流動機理。因此，需要在滲透率宏觀測試的基礎上，結合滲透模擬方法進行對比研究。目前，滲透模擬研究方法主要分為兩種：基于孔隙特征-試驗測試相結合的經驗公式(例如，Katz-Thompson公式[3])和基于三維孔隙結構的滲流模擬(例如，孔隙網絡模型[4]、計算流體力學方法[5]和格子Boltzmann方法[6])。

經驗公式則是在滲透性和水泥基材料孔隙特征測試數據的基礎上，建立的孔隙特征與滲透性的相互關系。Katz-Thompson公式以壓汞法所得孔隙結構特征為依據，引入孔隙撓曲度(即，連通路徑的真實長度與路徑兩端點直線距離的比值)，進行混凝土滲透性的預測，并取得了較好的預測效果[3]。可是，Garboczi等[7]的研究表明，僅有當孔隙繞曲度為570時，Katz-Thompson公式才能與實測滲透性吻合，這說明Katz-Thompson公式并不具有普遍適用性。相比之下，基于三維孔隙結構的直接模擬不僅可以預測水泥漿體的滲透性，而且可以展示硬化水泥漿體孔隙中流體的傳輸過程。孔隙網絡模型考慮了多孔結構的撓曲和孔喉效應，但由于簡化模型忽視了部分孔隙的連通性和孔壁的粗糙度，導致其計算結果與實際情況有所偏差[4]。計算流體力學以Naiver-Stokes方程為基礎，將流體視為連續介質，但計算流體力學結果容易受到網格劃分精度和復雜邊界處理的影響，較少用于水泥基材料等納米孔隙結構[5]。格子Boltzmann方法是一種介觀方法，它具有計算并行的優點，能夠處理復雜的邊界，彌補了計算流體力學方法的不足[6]。然而，以往研究較少將上述方法應用于水泥漿體的孔隙結構滲透率模擬中，更少用于對比氣體滲透測試結果，進而研究水泥基材料的孔隙滲透特征。

本研究以水泥漿體三維孔隙結構和壓汞試驗數據為基礎，分別采用了Katz-Thompson方程和格子Boltzmann方法預測水泥試樣的滲透率，分析了水泥漿體滲透模擬結果，并與氣體滲透率測試結果進行了對比分析，最終探討了水泥基材料的滲透機理。

1 實 驗

測試樣品為水泥凈漿，采用水泥為普通硅酸鹽水泥P·O 52.5，水灰比為0.4，養護方式和養護時間為水中養護150 d。

1.1 壓汞試驗

取出制備好的水泥漿體試塊，將其切割成邊長約為0.8 cm的立方體塊狀，然后放置于40 ℃烘箱內直至質量穩定后進行壓汞試驗。壓汞試驗采用美國麥克AutoPore IV 9510壓汞儀，壓力范圍設定為2.6 kPa～200 MPa，水泥漿體與汞的接觸角值選為140°，表面張力設為480 mN/m。

1.2 氣體滲透試驗

將養護完成的試樣，通過鉆孔取芯制備成直徑37 mm、高度20 mm的試塊，然后將試樣放置于40 ℃的烘箱內干燥，直至質量穩定。氣體滲透測試采用恒定流量法進行測定，氣體滲透儀器示意圖見圖1。首先，在進氣口通過緩沖氣罐提供恒定的進氣壓，同時排氣口無任何連接，直接排入大氣。然后，打開進氣口，開始氣體滲透率測試。每隔5 min測試排氣口氣體流量Q，直至氣體流動穩定為止，即相鄰兩個氣體流量Q差值小于5%。最終，按照式(1)和式(2)計算出混凝土的氣體滲透率。該方法基于廣義達西定律：

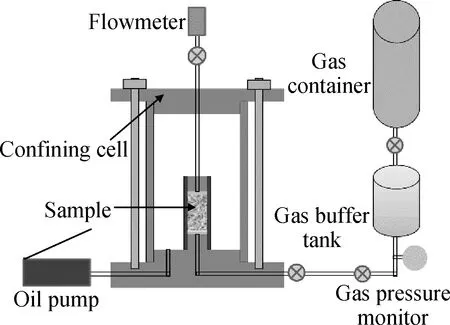
圖1 氣體滲透儀器示意圖[8]Fig.1 Schematic of gas infiltration equipment[8]

(1)

(2)

式中：h為試樣高度；P1為進氣口的氣體壓力；P0為出氣口的氣體壓力。

1.3 FIB/SEM掃描

試樣養護完成后，通過切割、粗磨和氬離子拋光，將試樣制備成面積約為1 cm2、厚度約為0.3 cm的薄板試樣。然后，采用德國蔡司Crossbeam 540聚焦離子束掃描電鏡(FIB/SEM)對試樣中兩處水泥漿體區域進行三維掃描。掃描完成后，采用美國Image J 1.52軟件對圖像進行降噪、分割等處理，所得試樣信息如表1所示。最后，通過美國FEI Avizo 8.01三維軟件進行孔隙結構三維重建，如圖2所示。FIB/SEM的制樣、掃描、圖像處理和三維重構方法詳見文獻[9]。

表1 硬化水泥漿體FIB/SEM圖像信息Table 1 Information of hardened cement paste FIB/SEM images

圖2 硬化水泥漿體FIB/SEM試樣圖像Fig.2 FIB/SEM images of hardened cement paste

1.4 滲透率預測

(1)Katz-Thompson方程

Katz和Thompson根據逾滲理論建立了滲透率與孔隙率和孔隙特征半徑的經驗方程，即Katz-Thompson(K-T)方程[3,7]：

(3)

其中：F=φ/τ為形狀參數；τ為孔隙網絡連通路徑的撓曲度；φ為連通孔隙率；dc為壓汞試驗獲取的孔隙特征直徑；1/226為試驗擬合常數。通過該方程的建立，可以利用上述參數預測混凝土的滲透率。

為了獲得上述參數，可以采用Avizo軟件中的Magic Wand分割工具獲取FIB/SEM圖像孔隙結構中的連通孔隙，以此計算出孔隙結構的連通孔隙率φ。孔隙特征直徑dc則可以分別采用連續孔徑分析法和模擬壓汞法分別計算圖像的連續孔徑分布曲線和模擬壓汞曲線，以此獲得其孔徑特征直徑[9]。撓曲度τ則可以根據孔隙網絡模型-居中軸線法進行計算：首先，采用居中軸線法將三維的孔隙結構簡化為節點和路徑構成的三維孔隙網絡模型；然后，根據節點坐標、路徑長度/體積等信息，采用自編程序計算兩平行平面所有連通路徑的累計距離和直線距離，由此計算所有路徑的撓曲度τ及其平均值τmean。

(2)格子Boltzmann法

格子Boltzmann方法是一種主要適用于微納米孔隙流體傳輸的方法。不同于分子動力學(Molecular Dynamics, MD)關注每個粒子的運動狀態，格子Boltzmann方法研究粒子運動狀態的分布函數，故擁有更大的流體計算尺度。同時，格子Boltzmann方法允許并行計算提高計算效率，且能夠有效處理三維孔隙結構的復雜邊界。研究采用D3Q19模型對晶格速度進行離散，采用單松弛(LBGK)方程描述滲流空間中流體速度的變化，其中單松弛(LBGK)方程表示為[10]：

(4)

最后，根據達西定律計算孔隙結構的滲透率：

(5)

式中：u為流體的平均速度。

2 結果與討論

2.1 氣體滲透率

對三個水泥樣品進行氣體滲透率測試，測試試樣的固有氣體滲透率分別為3.82×10-18m2、3.94×10-18m2和7.29×10-18m2。由上可見，三個試樣測試結果差異相對較小，且該差異主要為試樣制備和干燥過程中產生的樣品差異。該結果與以往研究結果[11](水灰比0.4，養護28 d，3.9×10-18～8.0×10-18m2)較為相似，均處于相同數量級，表明該測試結果較為穩定、可靠，受水泥開裂、漏氣等實驗因素影響較小。

2.2 水泥孔徑特征

根據侵入壓強設定，壓汞試驗測得水泥試樣的最小孔隙直徑約為6 nm，試樣孔隙率為14.32%，其孔徑分布曲線如圖3所示。同以往研究結果相似，壓汞試驗測得的孔隙結構主要集中在10～300 nm，其最可幾直徑為34 nm。

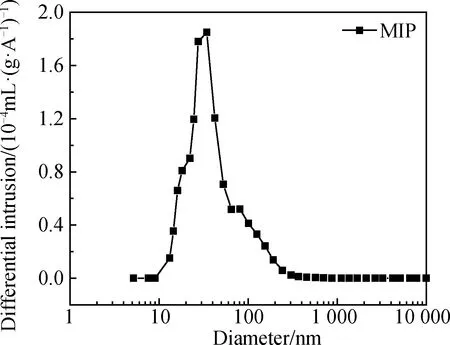
圖3 壓汞測試孔徑分布曲線Fig.3 Pore size distribution by MIP test

模擬壓汞法(MIP)和連續孔徑分析法(CPSD)所得的孔徑分布曲線如圖4所示。對于Cement 1和Cement 2，模擬壓汞法曲線形狀與壓汞試驗較為相似，其峰值均為42 nm，該結果僅比壓汞試驗結果略大；對于連續孔徑分析法，其曲線呈現兩個較大的峰值，分別為56 nm和84 nm，為壓汞試驗結果的1.6～2.5倍。這是由于連續孔徑分析法從孔隙結構內部“侵入”，因而避免壓汞試驗引起的“墨水瓶”效應[9]。此外，如圖4所示，模擬壓汞法中6種模擬壓汞起始面獲得的模擬壓汞曲線均較為相似，這也表明試樣各向同性較為明顯。對比以往研究結果[9](模擬壓汞法50～60 nm，連續孔徑分析法70～90 nm)，本研究模擬壓汞法和連續孔徑分析法的結果略小，這可能是由于不同水泥品種、養護條件和試樣選區所致。

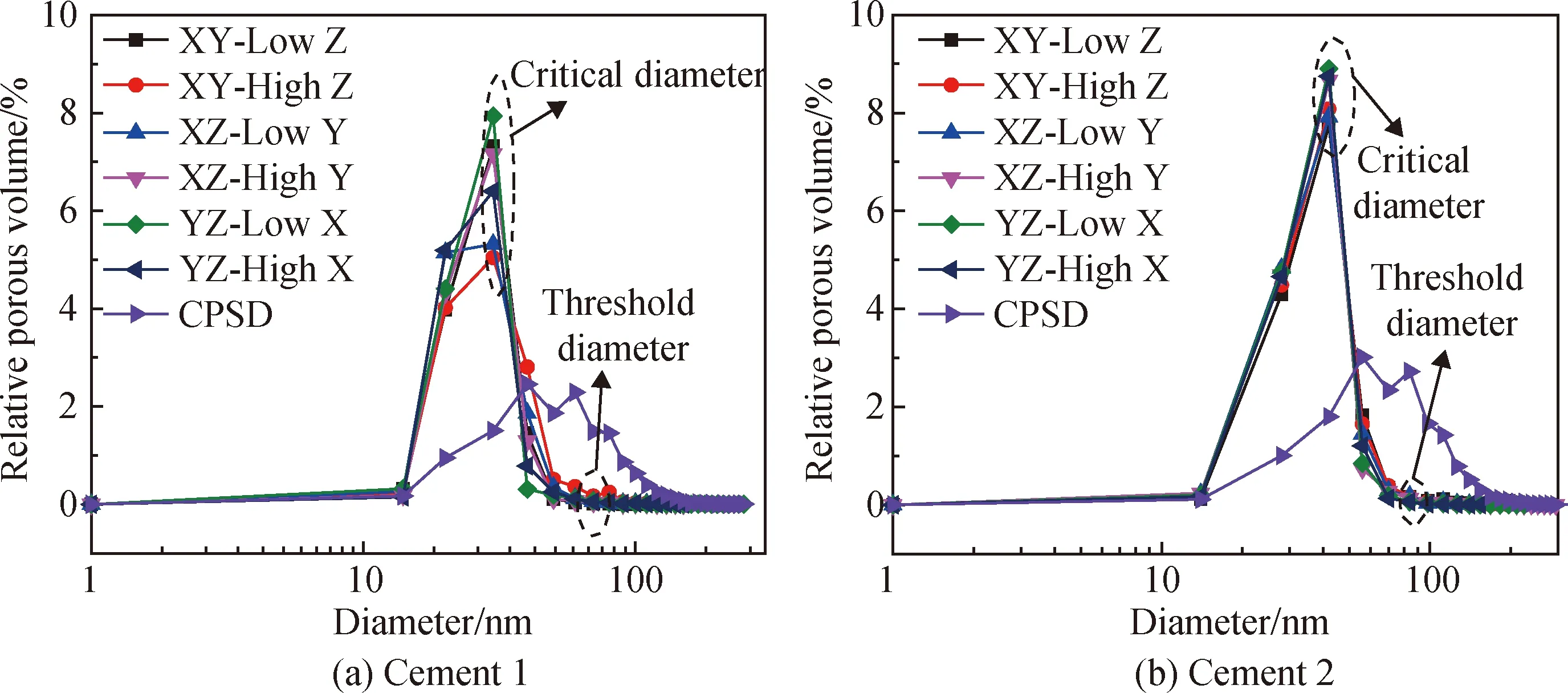
圖4 模擬壓汞法和連續孔徑法計算孔徑分布曲線Fig.4 Pore size distribution by simulated MIP and continuous PSD

采用中心線法提取兩個試樣的孔隙網絡模型(見圖5)，并利用自編程序對模型進行分析，得到兩個試樣在三個方向上的撓曲度頻率分布曲線，如圖6所示。Cement 1在三個方向上的撓曲度均較為相似，其峰值均為2.5，其中Y方向和Z方向其曲線近乎重疊。這表明Cement 1的孔隙結構在三個方向上的撓曲度較為相近，也表明其具有較好的各向同性。同時，路徑撓曲度主要集中在1.5～4之間，表明孔隙網絡較為連通，流體介質傳輸撓曲程度較好。相反，Cement 2在三個方向上的撓曲度差異較大：在X方向撓曲度與Cement 1相似，均集中在1.5～4之間，且其峰值為2.5；在Y方向上，盡管其撓曲度較為分散，不具有明顯的峰值，但連通路徑撓曲度仍主要集中在1.5～4之間；在Z方向上，撓曲度分散度更大，曲線沒有明顯峰值，且撓曲度大于4的路徑約占總路徑數的30%。這表明Cement 2撓曲度上具有較強的各向異性。該各向異性可能是由于試樣中的水泥水化程度不夠均勻，存在部分未水化的區域，導致孔隙的撓曲度在不同方向存在差異。

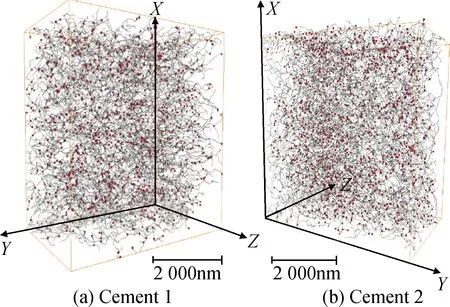
圖5 FIB/SEM試樣孔隙網絡模型Fig.5 Pore network model of FIB/SEM samples

2.3 滲透率預測

(1)Katz-Thompson方程

由于Katz-Thompson方程是源于逾滲理論和壓汞試驗的半經驗公式，因此，研究采用壓汞試驗結果和模擬壓汞法獲得的數據進行滲透率計算。可是，在Katz-Thompson方程中對于特征孔徑dc尚無統一規定，以往研究通常采用臨界直徑或閾值直徑(見圖4)進行滲透率計算，故本研究采用上述兩種直徑進行滲透率預測。由于壓汞試驗無法獲取撓曲度，故采用Cement 1和Cement 2的平均撓曲度進行計算，計算結果如表2所示。

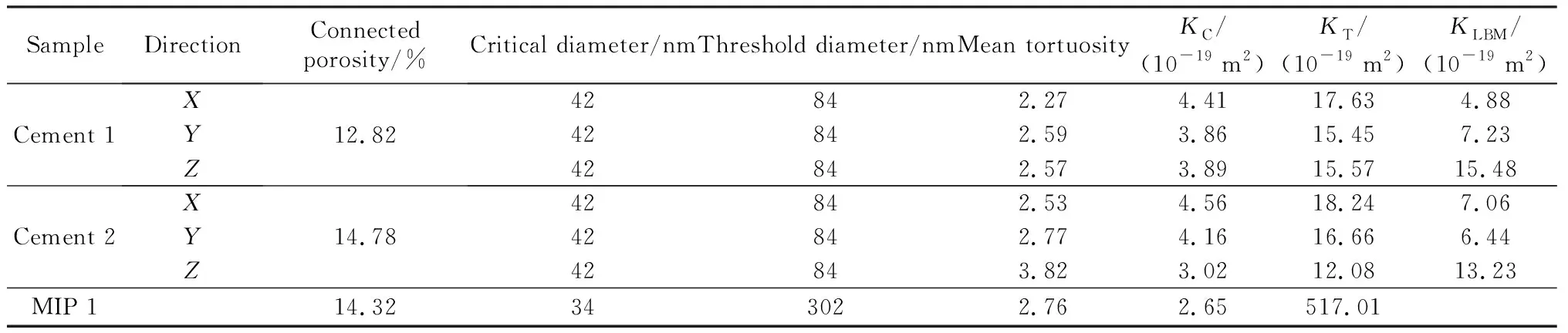
表2 Katz-Thompson方程和格子Boltzmann方法滲透率預測Table 2 Permeability prediction by Katz-Thompson equation and lattice Boltzmann method

結果表明，Cement 1和Cement 2的連通孔隙率、特征孔徑和撓曲度平均值均較為相似，甚至相同，因此兩個試樣的滲透率預測結果整體相差不大。對于同一試樣的不同滲透方向，僅Cement 2在Z方向上連通路徑撓曲度較大(見圖6(b))，導致其滲透率略低，其它方向滲透率差異較小，均主要集中在3.86×10-19～4.56×10-19m2或15.45×10-19～18.24×10-19m2。此外，采用壓汞試驗(MIP 1)和模擬壓汞法(Cement 1和Cement 2)的臨界直徑所預測的氣體滲透率處于同一數量級，然而當采用閾值直徑時，壓汞試驗所預測的氣體滲透率是模擬壓汞法的約28～43倍，為517.01×10-19m2。這是由于壓汞試驗所得閾值直徑(302 nm)遠大于模擬壓汞法的結果，其原因為壓汞試驗中不可避免地引入了微裂縫、氣孔等微米或亞微米孔隙，而此類孔隙在Cement 1和Cement 2試樣中并未發現。

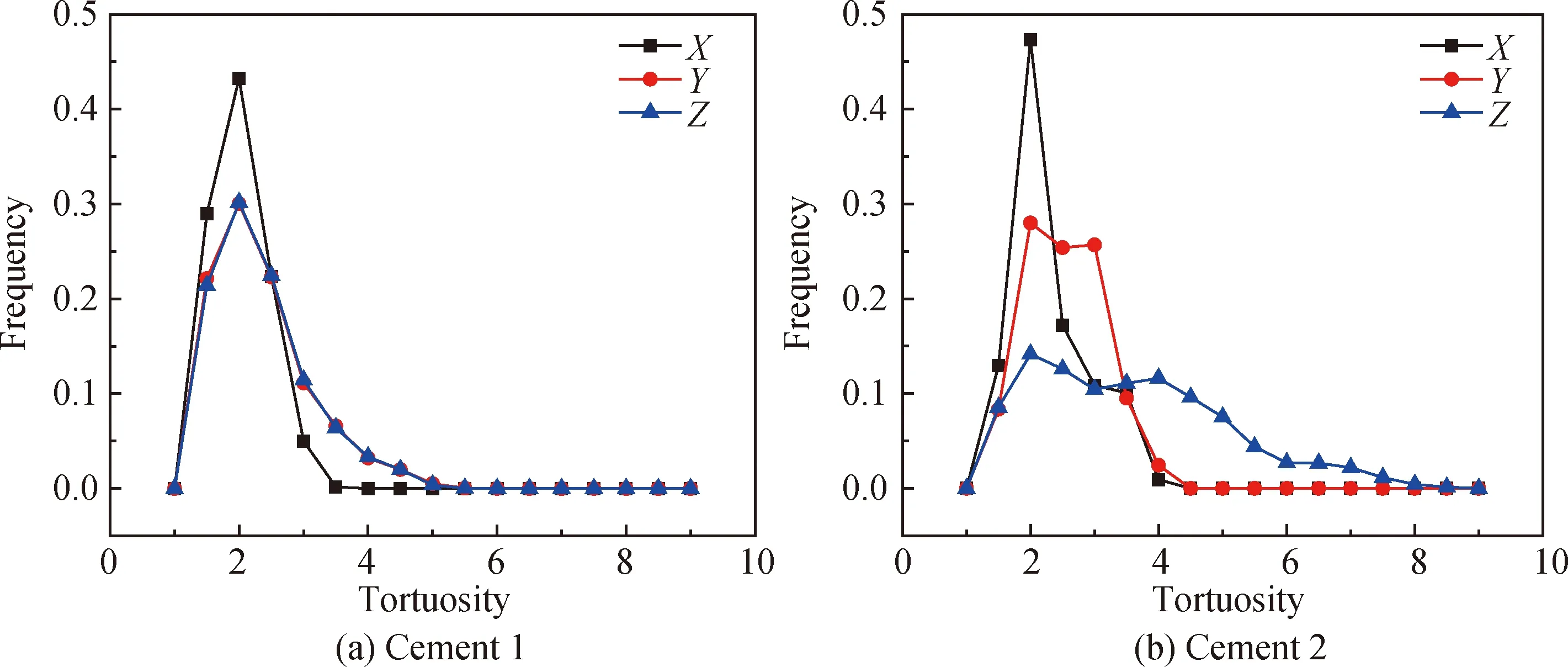
圖6 FIB/SEM試樣撓曲度分布曲線Fig.6 Tortuosity distribution of FIB/SEM samples

然而，無論采用壓汞試驗或者模擬壓汞試驗結果，采用不同特征直徑均會導致滲透率預測結果產生較大差異。對于模擬壓汞試驗，若采用臨界直徑，其滲透率KC為3.02×10-19～4.56×10-19m2；若采用閾值直徑，其滲透率KT則放大約4倍，為12.08×10-19～18.24×10-19m2。依據目前結果較難判斷應當采用何種特征直徑進行滲透率計算，需要對比氣體滲透測試結果和格子Boltzmann法預測結果并進行探討分析。

(2)格子Boltzmann法

對于Cement 1和Cement 2，格子Boltzmann方法預測FIB/SEM試樣滲透率KLBM結果見表2。格子Boltzmann方法預測結果在X方向和Y方向與Katz-Thompson方程中臨界直徑的預測結果較為相似，約4×10-19m2，而在Z方向則與Katz-Thompson方程中閾值直徑的預測結果相近，約12×10-19～15×10-19m2。這表明Katz-Thompson方程的預測結果受特征直徑影響較大，且不能真實準確地預測孔隙結構的滲透率，但其預測結果與格子Boltzmann方法基于真實孔隙的模擬結果具有數量級的準確度，可以用于滲透率的粗略計算。

Cement 1在X方向、Y方向和Z方向的滲透速率分布如圖7所示。在X方向和Y方向滲透圖中，其滲透速度普遍較小(流速較暗)且滲透路徑較細。然而，在Z方向，盡管Cement 2的撓曲度較大，但是流體滲流速度普遍較大且滲流路徑較多，其反而具有更高的滲透率。可見，有效降低水泥漿體中的孔隙尺寸，是提高水泥基材料耐久性的關鍵措施。

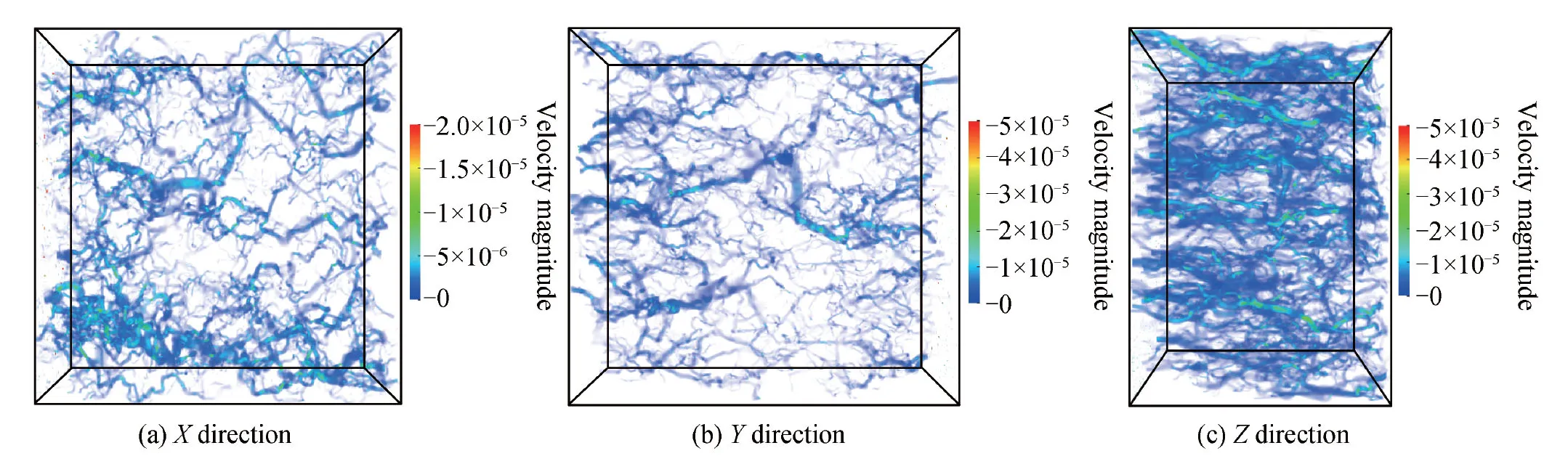
圖7 格子Boltzmann方法模擬Cement 1孔隙結構滲透速率Fig.7 Percolation velocity of porous volume of Cement 1 by lattice Boltzmann method

(3)滲透率測試與預測結果對比

由上可知，格子Boltzmann方法滲透率預測基于具體孔隙結構，能夠較好地模擬氣體在孔隙中的流動，且能夠體現出孔隙結構的各向異性，其預測滲透率結果為4.88×10-19～15.48×10-19m2。然而，該預測結果相較氣體滲透率測試結果(3.82×10-18～7.29×10-18m2)較小，這是由于兩者測試試樣的尺寸具有較大的差異。氣體滲透率測試采用厘米級別的宏觀硬化水泥漿體，其內部孔隙結構既包括FIB/SEM觀測到的10～500 nm的毛細孔，也包含了水泥成型、水化、干燥過程中產生的微裂縫、氣孔等微米乃至毫米級別的孔隙結構。盡管微裂縫和氣孔等孔隙結構較為獨立或僅局部連通，仍然可以大大縮短氣體在水泥試樣內部的滲透路徑，使得氣體滲透率有提高。結果表明，氣體滲透測試結果相較模擬結果僅提升2～10倍，也表明水泥漿體中毛細孔依然是滲透的主要路徑，而氣孔、微裂縫僅在局部起到了提高氣體滲透率的作用。否則，若連通孔隙為亞微米的大孔，則以壓汞試驗所得的閾值直徑為基礎，采用Katz-Thompson方程預測的滲透率將為實際測試結果的7～13倍，格子Boltzmann方法計算結果的14～130倍。

3 結 論

(1)硬化水泥凈漿氣體滲透率的測試結果為3.82×10-18～7.29×10-18m2。

(2)Katz-Thompson方程的預測結果具有數量級的準確度，但不能真實準確地預測孔隙結構的滲透率，僅可以用于滲透率的粗略計算。

(3)格子Boltzmann方法以真實孔隙結構為基礎，能夠準確地預測水泥漿體的本質滲透率，為4.88×10-19～15.48×10-19m2。

(4)氣體滲透測試結果約為模擬結果的2～10倍，這表明水泥漿體中毛細孔依然是滲透的主要路徑，而氣孔、微裂縫僅在局部起到了提高氣體滲透率的作用。