AC-13級配鋼渣瀝青混合料 粘彈塑本構模型研究

曾國偉，劉浩軒，白 凡，吳 亮，周 鵬

(1.武漢科技大學理學院，武漢 430065；2.湖北省冶金工業(yè)過程系統(tǒng)科學重點實驗室，武漢 430081)

0 引 言

鋼渣是冶煉鋼鐵的主要副產(chǎn)品，我國鋼渣年產(chǎn)量較大，相比國外有效利用率很低，常被當作廢棄物處理[1]。將鋼渣作為瀝青混合料集料能有效提高瀝青混合料性能，同時也解決了鋼渣的有效利用問題，實現(xiàn)了資源節(jié)約和環(huán)境友好，符合可持續(xù)發(fā)展戰(zhàn)略的要求。

將鋼渣應用于瀝青混合料，可以改善混合料力學性能。鋼渣瀝青混凝土路面的承載能力、抗車轍能力、抗低溫開裂能力和抗水損害能力均超過同級配的石灰石瀝青混凝土。Hassan等[2]以AC-20級配為基礎，將鋼渣顆粒作為細集料替代石灰石，進行配比轉換，并進行實驗驗證。Xue等[3]對鋼渣集料密度、吸水率、磨光值、粘附性等基本性質分析后發(fā)現(xiàn)，高爐鋼渣完全可以作為粗集料應用于瀝青混凝土中。李燦華等[4]針對鋼渣瀝青混合料路面8年服役性能進行試驗，表明鋼渣瀝青路面性能各項指標均優(yōu)于傳統(tǒng)路面。李建華[5]對鋼渣瀝青混合料路用性能進行了比較全面的研究，驗證了鋼渣作為瀝青面層材料的優(yōu)異性能。然而，已有的研究大多以馬歇爾穩(wěn)定度、間接拉伸強度、勁度模量及疲勞壽命等參數(shù)評價鋼渣瀝青混合料的性能[6-11]，忽略了非線性粘彈塑模型參數(shù)對車轍的影響。

瀝青混合料在循環(huán)車載作用下不斷積累的永久變形是車轍形成的直接原因。針對瀝青混合料力學變形行為的本構關系頗受工程界的關注。研究者們嘗試采用變形分解的方法將粘彈性、粘塑性進行組合[12-14]，在低溫小應力條件下，粘彈性部分常采用微分型模型[15-17]進行描述，而在高溫和較大應力下，瀝青混合料呈現(xiàn)非線性特點，材料的應力應變關系不再滿足線性疊加原理，粘彈性模型常采用Schapery積分型模型，粘塑性部分則主要采用UZAN模型、PERZYNA模型和曹樹剛模型等時間應力相關函數(shù)進行描述[18-19]。可以看出，研究鋼渣瀝青混合料的粘彈塑力學性質對于研究和預測鋼渣瀝青路面的車轍形成具有重要意義。因此，有必要針對鋼渣瀝青混合料非線性蠕變回復行為建立相應的粘彈塑本構模型。

本研究以粒徑2.36 mm為粗細集料分界線，將鋼渣作為粗集料，將石灰石作為細集料，按照AC-13級配制作鋼渣瀝青混合料試件，在25 ℃下開展一系列的蠕變回復實驗，將鋼渣瀝青混合料變形分解成瞬時彈性、粘彈性和粘塑性變形，采用Schapery模型描述瞬時彈性、粘彈性變形，采用改進Swchartz模型描述粘塑性變形。通過擬合實驗數(shù)據(jù)確定模型參數(shù)，并利用模型預測任意應力下的蠕變回復曲線，驗證模型的合理性。

1 蠕變實驗

1.1 實驗材料與級配

瀝青型號為茂名石化70號石油瀝青，粗集料采用河北勝利轉爐鋼渣，粒徑為2.36～16.2 mm，細集料采用石灰?guī)r，粒徑為0.075～2.36 mm，礦粉為石灰石研磨而成，以上集料經(jīng)篩分后待用。原材料各項物理力學指標見表1和表2。實驗材料滿足《公路瀝青路面施工技術規(guī)范》(JTG F40—2004)和《公路工程瀝青及瀝青混合料試驗規(guī)程》(JTG E20—2011)的要求。

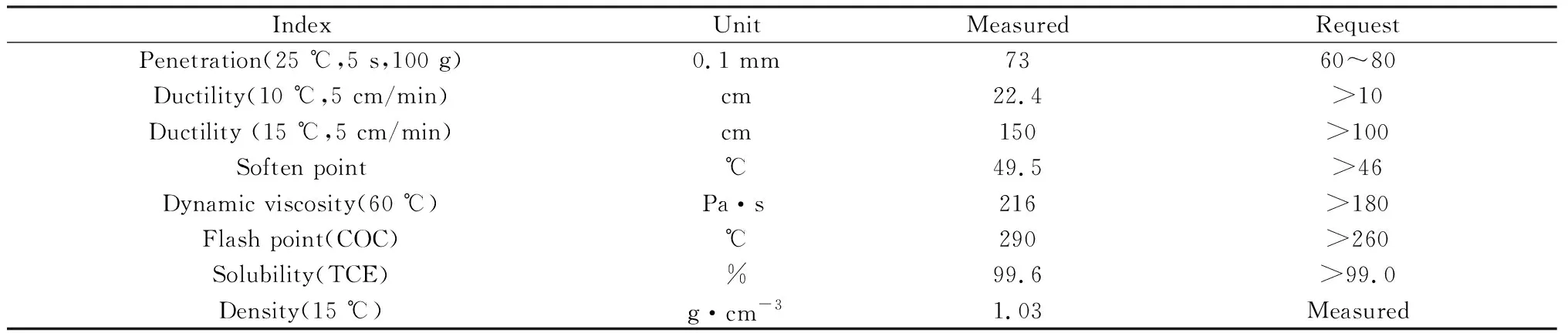
表1 石油瀝青技術指標Table 1 Technical indicators of asphalt

表2 集料性能技術指標Table 2 Technical indicators of aggregate

AC-13是最常見的連續(xù)型密級配，由于鋼渣顆粒與石灰石密度相差較大，本文采用體積法換算得到鋼渣瀝青混合料AC-13級配組成設計，圖1為全部采用傳統(tǒng)集料與粗集料采用鋼渣的AC-13級配曲線。另外，通過試制發(fā)現(xiàn)，當油石質量比為5.3%～6.1%時，鋼渣瀝青混合料試件瞬時塑性變形較小；油石比為4.5%～5.3%時，鋼渣瀝青混合料試件粘塑性較小，因此本文確定油石比為5.3%。

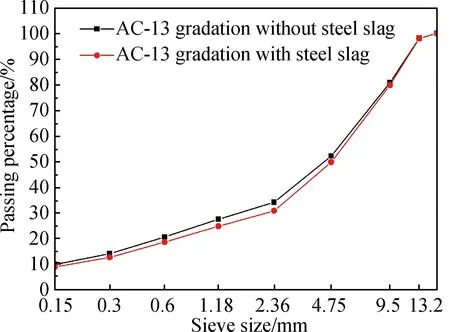
圖1 鋼渣瀝青混合料級配曲線Fig.1 Gradation curves of steel slag asphalt mixture

1.2 測試方法

依照《公路工程瀝青及瀝青混合料試驗規(guī)程》(JTG E20—2011)，采用擊實法制作101.6 mm、高度63.5 mm的標準馬歇爾試件，如圖2所示。將成型的試件進行編號，測量試件的直徑與高度，允許的偏差為±0.5 mm。對所制成的鋼渣瀝青混合料試件進行一系列室內(nèi)單軸壓縮蠕變實驗研究。采用配置有恒溫裝置的電子萬能實驗機，環(huán)境溫度控制在25 ℃±0.5 ℃，編制加載程序，進行應力遞增的蠕變回復實驗、單一蠕變實驗和單次蠕變回復實驗，加載歷史詳見表3和表4。由計算機自動采集實驗數(shù)據(jù)，每組實驗重復三次，采用平均值繪制時間-應變曲線。

圖2 鋼渣瀝青混合料實驗試件Fig.2 Specimens of asphalt mixture with steel slag

表3 應力遞增的蠕變回復試驗加載歷史Table 3 Loading history of multiple-stress repeated creep-recovery test

表4 單次蠕變與蠕變回復試驗加載歷史Table 4 Loading history of single creep and creep-recovery test

2 模型本構方程

對于單一蠕變回復實驗，瀝青混合料應變可分解為四部分，如圖3所示。時間t=0時刻加載，產(chǎn)生瞬時彈性應變εe和瞬時塑性應變εp，保載時產(chǎn)生粘彈性應變εve和粘塑性應變εvp；t=t0時刻卸載，產(chǎn)生回復瞬時彈性應變εe，卸載足夠長時間后殘余瞬時塑性應變εp和粘塑性應變εvp。總蠕變應變ε(t)可表示為：

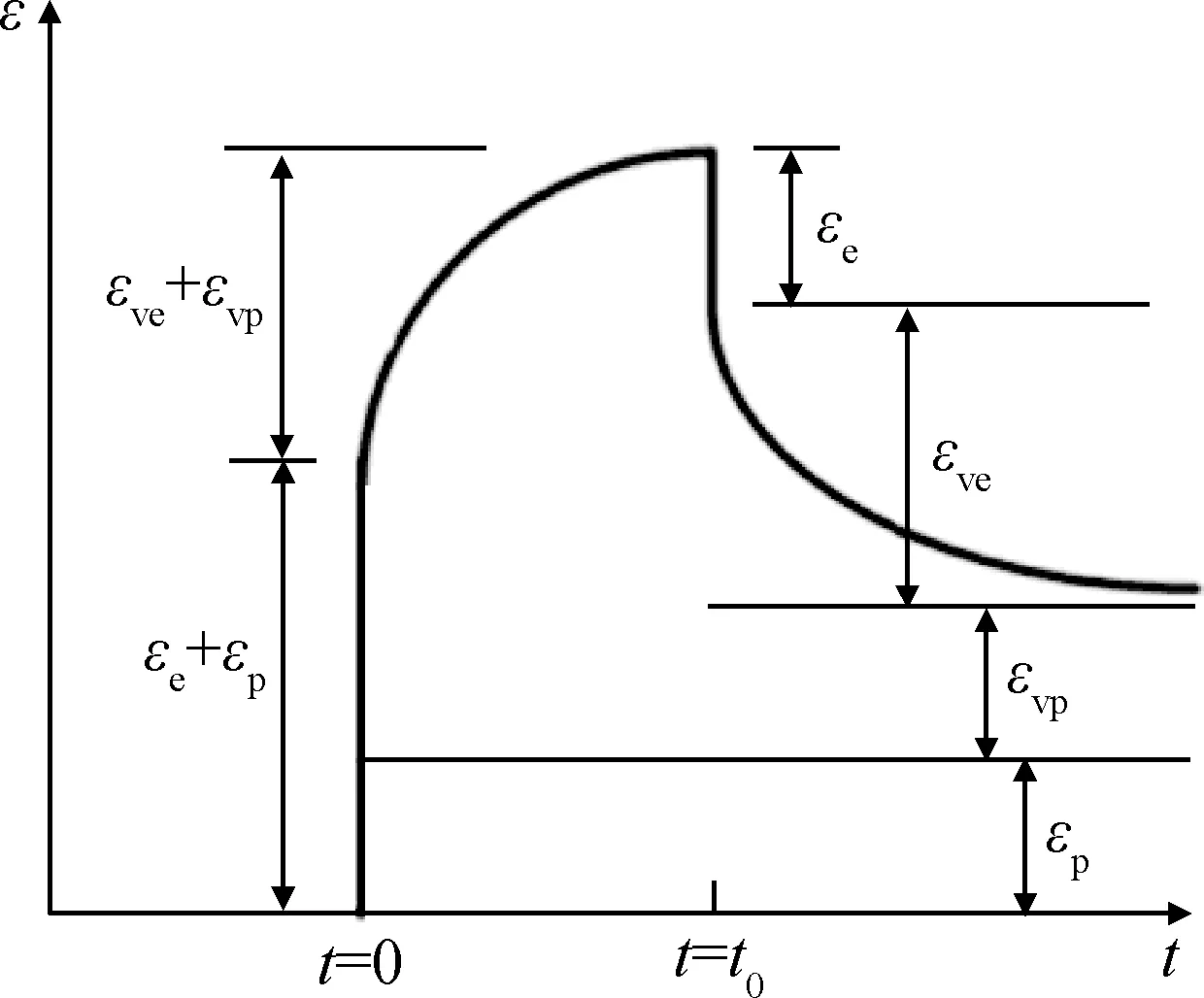
圖3 蠕變變形分解圖Fig.3 Diagram of creep deformation decomposition

ε(t)=εe+εp+εve+εvp

(1)

可回復變形包括瞬時彈性變形εe和粘彈性變形εve，采用兩參數(shù)的簡化Schapery非線性粘彈性模型來描述。

(2)

式中：εe為瞬時彈性部分；D0為瞬時彈性蠕變?nèi)崃浚籫0、g2為非線性參數(shù)，只與應力σ有關；t為時間；τ為應為σ作用下的時間變量；dτ為時間增量；ΔD為依賴時間的短時蠕變?nèi)崃浚捎肞rony級數(shù)表示：

(3)

式中：D(t)為時間t相關的蠕變?nèi)崃亢瘮?shù)；λi和Di分別為第i個遲滯時間倒數(shù)和遲滯柔量；n為Prony級數(shù)的總項數(shù)，本文取n=5。對于單一蠕變回復實驗，材料的粘彈性響應可表示為：

(4)

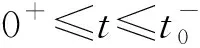
(5)

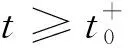
(6)

在回復過程中的遲滯應變?yōu)椋?/p>

(7)

根據(jù)式(7)，對于任意兩種應力下(如σ0=σ1和σ0=σ2)的單次蠕變回復實驗，回復階段應變滿足：

(8)

式中：βσ為轉換系數(shù)。

粘塑性模型包括瞬時塑性應變εp和粘塑性應變εvp，進一步精簡文獻[20]的改進型Schwartz粘塑性模型，構成新的兩參數(shù)粘塑性模型：

(9)

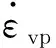
基于式(1)、(2)和(9)，鋼渣瀝青混合料本構模型可以表示為：

(10)

3 結果與討論

3.1 模型參數(shù)確定

參照文獻[20]，設定0.05 MPa為鋼渣瀝青混合料蠕變行為線性與非線性范圍應力分界點，在小應力(0.05 MPa以內(nèi))作用時，瀝青混合料在小應力條件下其變形通常是線性的，式(2)中所有與應力相關的參數(shù)為1，即g0=g2=1。此外，表3的應力遞增的蠕變回復實驗，回復階段時間足夠長，可以認定此段時間內(nèi)粘彈性變形完全回復。模型參數(shù)確定流程如下：

(1)應力遞增的蠕變回復試驗中的回復曲線，經(jīng)過平移減去相應的殘余應變，可看作不同應力下單次蠕變回復試驗的回復曲線。提取卸載時的瞬時應變εe,根據(jù)公式(2)，在小應力0.05 MPa下，確定D0，然后根據(jù)其他應力下的瞬時應變，確定不同應力下的g0值，并擬合g0(σ)函數(shù)。

(2)將每個循環(huán)步的回復應變減去急彈性應變，即可得到不同應力下的粘彈性應變曲線，以0.05 MPa的粘彈性曲線為參考曲線，根據(jù)公式(7)，擬合得到初始Di和λi值。

(3)根據(jù)公式(7)繼續(xù)擬合0.2 MPa的粘彈性曲線，確定該應力下的g2值，并根據(jù)公式(8)得到β(0.2MPa)，將0.2 MPa的粘彈性曲線整體除以β(0.2MPa)，與0.05 MPa曲線組合成新的0.05 MPa曲線，根據(jù)公式(7)，擬合修正Di和λi值。

(4)針對剩下的0.3 MPa、0.5 MPa、0.8 MPa和1.2 MPa下的粘彈性曲線，重復第(2)、(3)步驟。得到不同應力下的g2值，并擬合g2(σ)函數(shù)，并得到最終的Di和λi值。

(5)將實驗總應變減去步驟(1)～(4)確定的急彈性和粘彈性應變，得到粘塑性應變，根據(jù)公式(9)，采用改進歐拉法，擬合得到粘塑性參數(shù)k、p值。

綜合以上步驟，編寫Matlab計算程序，可以擬合計算出模型參數(shù)值，結果見表5。圖4和圖5分別為應力遞增的蠕變回復試驗、單次蠕變實驗值與模型擬合值的對比，可以看出，實驗數(shù)據(jù)與模型擬合曲線吻合良好，表明模型本構模型與實驗變形規(guī)律一致，并具有較好的精度。另外，模型分離出各組分應變值，其中粘塑性應變不可恢復，且明顯大于其他部分應變，表明本文模型物理意義明確，較好地反映了25 ℃下鋼渣瀝青混合料的非線性蠕變回復變形特征。相較于Bai等[20]模型，本文模型在保證擬合精度的同時，待確定的參數(shù)數(shù)量更少。

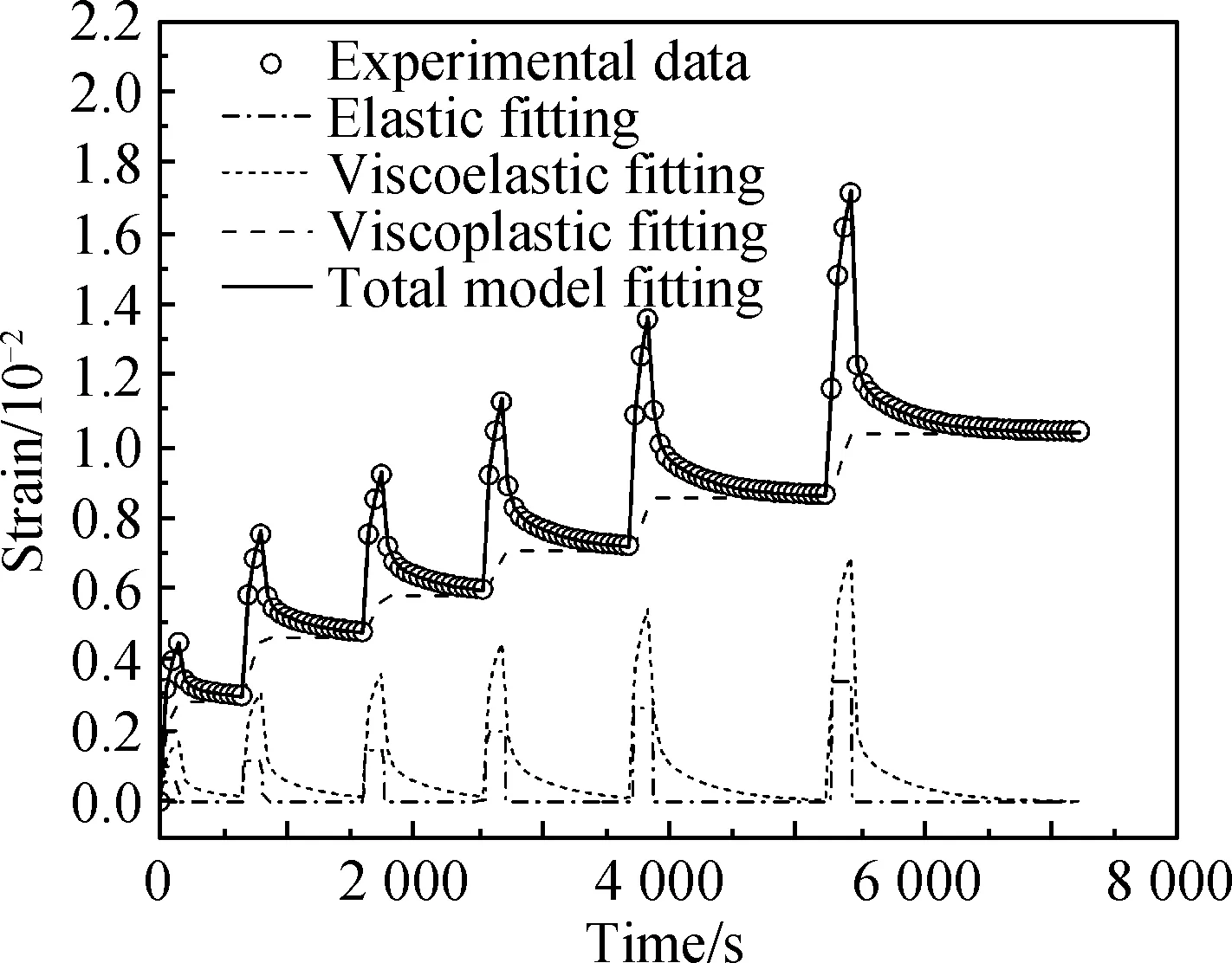
圖4 應力遞增蠕變回復實驗曲線與模型擬合曲線Fig.4 Experimental data and model fitting curves of multiple-stress repeated creep-recovery test

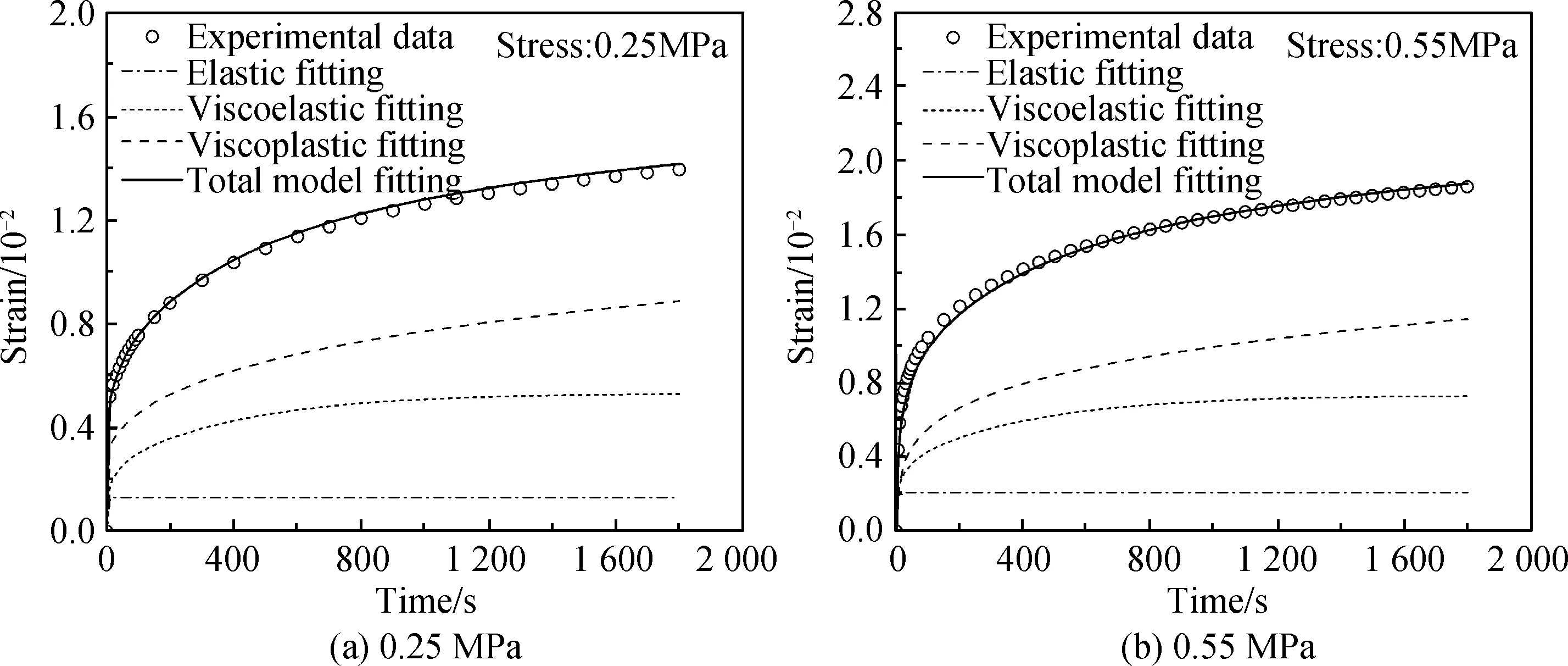
圖5 單一蠕變實驗曲線與模型擬合曲線Fig.5 Experimental data and model fitting curves of the single creep test

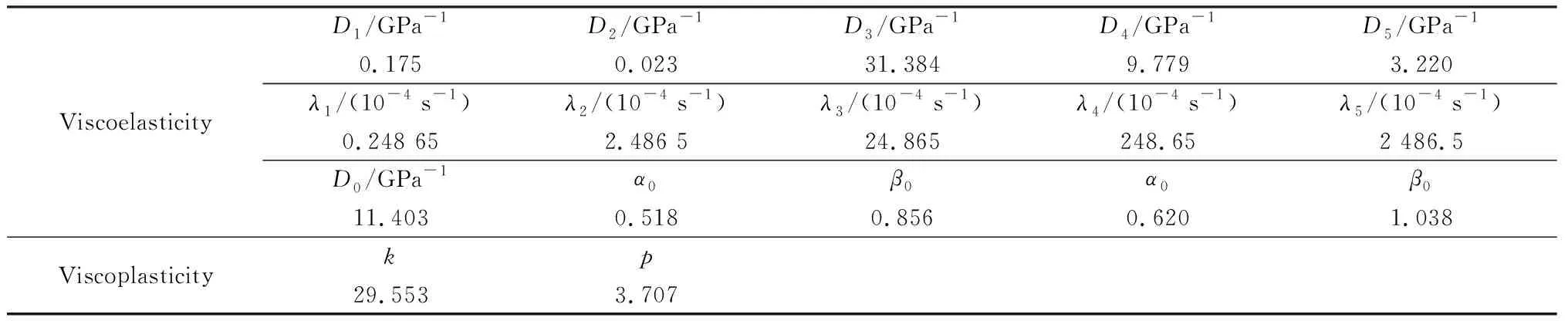
表5 本文模型參數(shù)確定值Table 5 Material parameters involved in the proposed model

3.2 模型試驗預測

為了驗證模型的合理性，將表5的模型參數(shù)，代入到公式(3)、(9)和(10)，即可預測任意應力下的蠕變回復變形規(guī)律。本文針對0.4 MPa和1.0 MPa兩種應力下的鋼渣瀝青混合料單次蠕變回復變形進行預測，并與實驗結果進行對比，如圖6(a)、(b)所示。可以看出，預測值與實驗值在蠕變階段吻合較好，回復階段存在一定偏差，但預測變形曲線與實驗結果趨勢一致。因此，在不考慮試件隨機性的前提下，本模型可對任意應力下的單軸蠕變回復行為進行有效的預測。

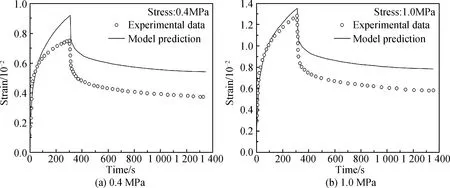
圖6 蠕變回復實驗曲線與模型預測曲線Fig.6 Comparison between experimental data and model prediction of the single creep-recovery tests

4 結 論

(1)針對AC-13級配鋼渣瀝青混合料開展了一系列蠕變回復實驗研究，并在此基礎上建立了混合料的粘彈塑本構模型，為鋼渣瀝青道路路面變形行為研究提供了理論依據(jù)。

(2)AC-13級配鋼渣瀝青混合料在蠕變回復實驗中的變形可以分解為急彈性、粘彈性和粘塑性3個部分，其中急彈性和粘彈性變形為材料可回復變形，粘塑性變形為材料不可回復變形。Schapery模型與改進Swchartz模型相結合的粘彈塑本構模型，適用于描述鋼渣瀝青混合料的蠕變回復行為，并且具有參數(shù)少、易于確定的優(yōu)點。

(3)在蠕變階段，模型預測的材料變形與實驗結果基本吻合。在回復階段，模型預測存在一定誤差，但預測的變形曲線與實驗結果趨勢一致。