深度揭示概念 感受負數價值

吳德娟 劉久成

【摘 要】負數來源于生活，同時具有構造特征。通過層層遞進的三個板塊，讓學生在生活實例中感受負數表示相反意義的量，在數軸模型中感受負數在數軸上的排列、有理數的有序性以及數的分類，在運算推理中感受負數能進行更多的運算、解決更多的實際問題，從而獲得對負數的本質認識，感受負數的價值，促進學生數學思維的發展。

【關鍵詞】小學數學 認識負數 教學片段 教學評析

負數雖然在小學教學中所占篇幅較少，但對負數的教學研究還是受到了廣泛關注。負數來源于生活，同時具有構造特征，為了讓學生清晰地認識負數概念，了解負數的來龍去脈，深切感受負數的價值，我們進行了以下教學嘗試。

教學片段1

師：同學們，在以前的學習中，我們認識了哪些數？

生：3、4、5、6等，這些是自然數。0.2、0.3、0.45等，這些是小數。

師：還有不同類的數嗎？

生：1— 2、1— 4、3— 4等，這些都是分數。

師：是啊，我們認識了整數、小數和分數。在人類歷史的長河中，人們曾用小石子、結繩和刻痕等來計數，隨著生產發展、交流增多、語言不斷豐富，于是逐漸產生了十進制計數法，并形成了現在的整數。人們在分物或測量的時候發現整數不夠用了，于是產生了分數和小數。今天我們還要來認識一種新數。（板書課題：認識負數）

【評析】本課一開始教師就提出：我們已經認識了哪些數？幫助回憶舊知，并對已經認識的整數、分數、小數的產生進行了概述，滲透了數學史教育，讓學生認識到數學不僅源于生活實踐，也源于理性思考，為學生從不同側面認識負數埋下了伏筆。

板塊一：在生活實例中初識負數

教學片段2

師：認識了整數、分數和小數，為什么還要認識負數呢？讓我們到生活中去尋找答案。如圖1所示，甲、乙兩組參加知識競賽，第一題過后，甲組答對，乙組答錯，兩組現在的比分各是多少？

生1：甲組得了20分，就用20來表示，乙組答錯，比0分還少20分，我認為用負20來表示。

師：-20會讀嗎？會寫嗎？表示什么意思？（板書：-20）

師：為什么乙組的得分不用以前學過的數表示？

生2：因為用以前的數表示比0分要高，而乙組比0分低。

生3：這個數比0小，要用負數來表示。

【評析】由于正負數的基本含義是具有相反意義的量，同時離不開“0”點的確定，而“0”點的確定帶有人為規定的特點。為分步推進，這里改變了教材中通過溫度計引入負數的做法，而是利用知識競賽的得分、失分這一生活中非常熟悉的事例，首先讓學生初步感受到正負數具有相反意義的特征。

教學片段3

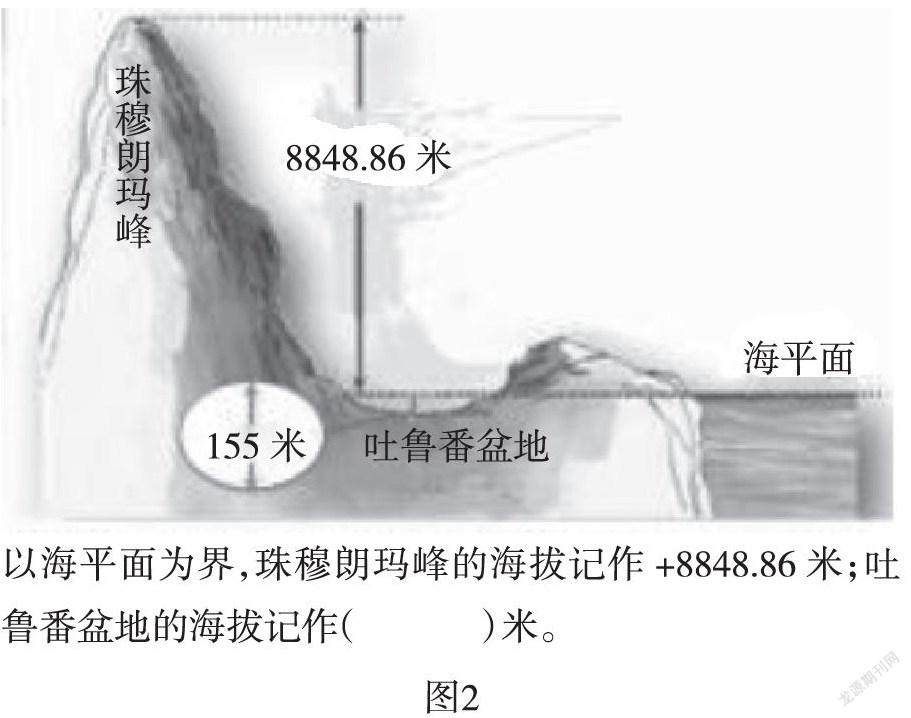
（出示海拔高度圖，如圖2）

師：吐魯番盆地該怎么表示？想一想為什么你會選擇用負數來表示。

生：我用-155來表示，因為吐魯番盆地比海平面還要低，海平面是0米，比0還要少就用負數表示。

師：同學們在觀察圖的時候，以海平面為分界點，海平面以上的高度用+8848.86來表示，海平面以下的高度用-155表示。

師：像-20和-155這樣的數都是負數，像20和+8848.86這樣的數都是正數。正數可以加正號，也可以不加，正號可以省略。負號可以省略嗎？

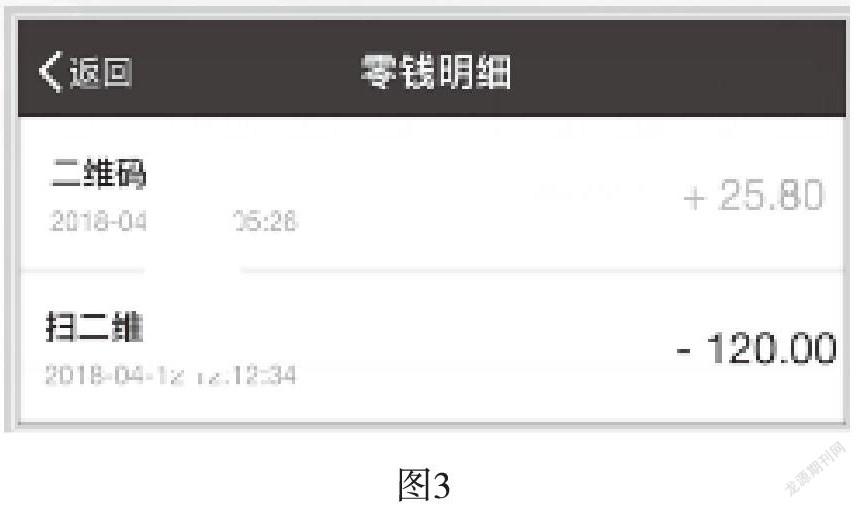
（出示微信賬單，如圖3）

師：下面是一份微信賬單，你能讀懂這兩個數分別是什么意思嗎？

生：+25.8元表示增加了的錢，-120元表示花去了120元。

師：這里的正數表示收入，那負數表示什么呢？

生：支出。

師：同學們能夠根據生活實際理解這兩個數的意思，支出的錢數可以用負數表示，收入的錢數可以用正數表示。

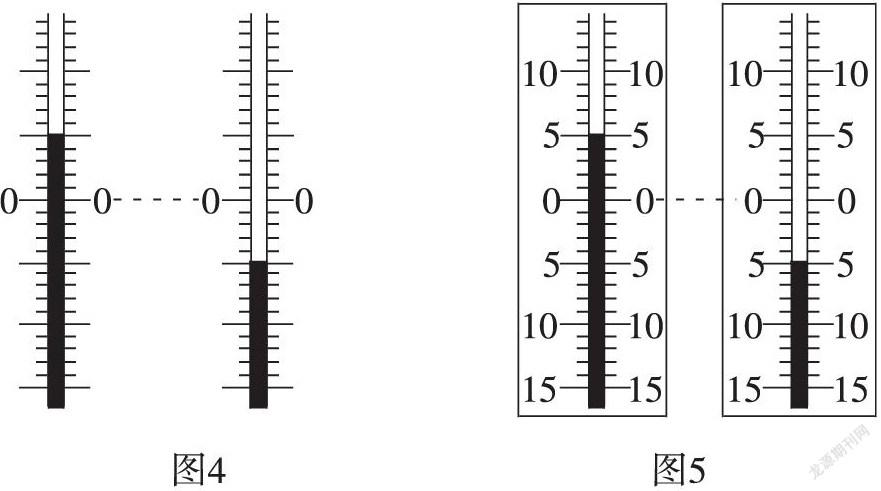
（出示溫度計，如圖4和圖5）師：圖4中這兩個溫度計的示數用正數還是負數來表示呢？

生：左邊的圖用正數表示，右邊的圖用負數表示。因為左邊的溫度比0攝氏度高，右邊的溫度比0攝氏度低。

師：現在能讀出圖5中兩溫度計顯示的溫度各是多少攝氏度嗎？

（學生讀并寫出溫度計上的溫度）

師：剛才大家在判斷用正數還是用負數表示的時候，首先需要確定什么？

生：先要確定0攝氏度在哪里。

師：0有什么作用？

生1：我認為0是把正數和負數隔開的。

生2：0是正數和負數中間的數。

生3：0的上面是正數，0的下面是負數。

生4：0在這兒是一個分界點，分界點的上面是正數，分界點的下面是負數。

師：大家說得都非常有道理，知道了0在表示正負數中的作用，它是正數和負數的分界點。

（板書：分界）

師：我們研究了4個問題，在每一幅圖中，既有正數也有負數，對照每一組數表示的含義，比一比，你有什么發現？（對照圖，見圖6）

生1：我發現右邊的都是正數，左邊的都是負數，我想中間應該是0吧。

生2：我發現正數表示的意思和負數是相反的，比如20分是得分，-20分是扣分，得分和扣分是相反的。收入和支出也是相反的，上和下也是相反的。

生3：我同意你的看法，我也認為正數和負數的意義是相反的。

師：這幾幅圖中，都含有相反的情況，得分和扣分，海平面以上和以下，收入和支出，當遇到這樣相反情況的時候，人們借用“-”號，創造了負數。有了負數，我們的表達會更加簡潔、準確。

【評析】通過記分表、海拔、賬單、溫度計四個問題的討論，從負數的自然意義（如記分表、賬單）到人為規定意義（如海拔、溫度計）的理解，讓學生充分感受到，正數、負數是表示相反意義的量，同時認識到“0”的定位作用。溫度計上的零上5攝氏度在左、零下5攝氏度在右，正好與板書設計的左右相反，這一設計不僅提醒了學生書寫時的規范，也在細節處強化了學生對概念的認識。通過四個問題的討論，最后概括出：當遇到相反的情況時，人們借用“-”號，創造了負數。學生在解決這四個問題的過程中體會到負數來源于生活實際，同時具有構造的特征。

板塊二：在數軸模型中感受負數

教學片段4

師：這是我們熟悉的數軸（如圖7），從0開始往右延伸，自然數都在上面，也可以找到分數和小數。大家想想負數在哪里？

生：從0開始向左延伸，負數應該在上面。（課件演示）

師：點A是多少，你怎么想的？（-1、-2、-3未標）

生1：點A表示-1，因為它在0的左邊。

生2：我要補充，它是在0的左邊，而且它和0相隔1格，所以是-1。

生3：我也認為是-1，因為在0的右邊一格是1，所以0的左邊一格就是-1。

師：大家說得很有道理，確實是用-1表示。觀察一下-1和1這兩個點，它們到0的距離相等嗎？

生：相等。

師：我們稱它們為一對相反的數。你能找出2、3、1.4這些數的相反數嗎？

（學生在數軸上指出）

師：觀察數軸你有什么發現，跟你的同桌說一說。

生1：我發現0的左邊的數比右邊的數多一個負號。

生2：如果把這條數軸沿中間的0對折，這些數會重疊在一起。

生3：我補充，點會重合在一起，數如果把負號去掉，也會重合在一起。

生4：他們的意思是，每一個正數和它相應的負數關于0點是對稱的，可以沿0點折起來重合在一起。

生5：正數在0的右面，負數在0的左邊。

師：同學們發現正數和它相應的負數關于0點是對稱的，有一個正數就能找到一個相應的負數，那么數軸上的每個點都是這樣的嗎？

生：不是，0沒有。

師： 0這個數很特殊，其實，它的相反數就是它自己。所以呢，0既不是正數也不是負數，它是正數和負數的分界。

師：如果把數軸上的數分為正數和負數兩類，大家同意嗎？如果不同意，那怎么改？

生：應該分為三類——正數、負數和0，因為0既不是正數也不是負數。

【評析】在數軸上討論負數比起生活中的負數要抽象一些，但它能整體地反映負數的特征，負數與正數的關系，強化了0的特殊性，以及0在認識正數、負數中的作用。

教學片段5

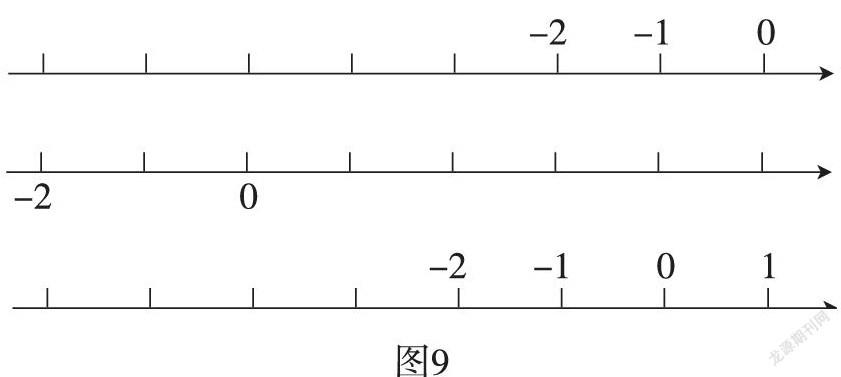
師：請同學們完成下面這道練習，在圖8中標一標。

（展示學生完成的練習結果，如圖9）

師：為什么同學們表示出的-2的位置不一樣呢？

生：因為0點的位置不一樣，所以-2的位置也不一樣。

師：雖然大家標的-2的位置不一樣，觀察三個學生的標法，有沒有什么共同點呢？

生：-2都在0左邊2格，也就是說如果確定了0的位置，那么它的左邊2格就是-2的位置了。

師：當我們要表示負數時，首先要確定0的位置，0的位置變化了，-2的位置也會變化。

【評析】出示數軸，并緊扣問題：負數在哪里？負數有多少？誰與誰是相反數？你有什么發現？展開討論，環環相扣，各個擊破。在數軸上認識負數，不僅形象直觀，滲透數形結合思想，而且有利于學生感受有理數的有序性。由此，學生不難發現規律：每一個正數都有相對應的負數;正數都比負數大;數軸上越往左的數越小，越往右的數越大;等等。

為了凸顯“0”的作用，教者特意安排了在數軸上標“-2”的練習，通過三種標法的對比，提問：同樣是表示“-2”，為什么點的位置不同？從而強調了“0”的定位作用，這就抓住了數軸上表示負數的關鍵。

板塊三：在運算推理中體會負數的應用

教學片段6

師：其實每一種數的產生，它的價值不僅是為了解決生活中的問題，數學科學的發展，同樣有需要。以熟悉的1和2為例，組成不同的算式，請用數來表示計算的結果。

1+2=? ? ? ? ? 1×2=? ? ? ? ? 1÷2=? ? ? ? ? ? 1-2=

師：1÷2能用整數表示嗎？為什么？

生：1÷2不能用整數表示，因為不夠1個了，用1— 2表示。

師：在除法運算中，不能整除時，我們可以用分數或小數來表示。

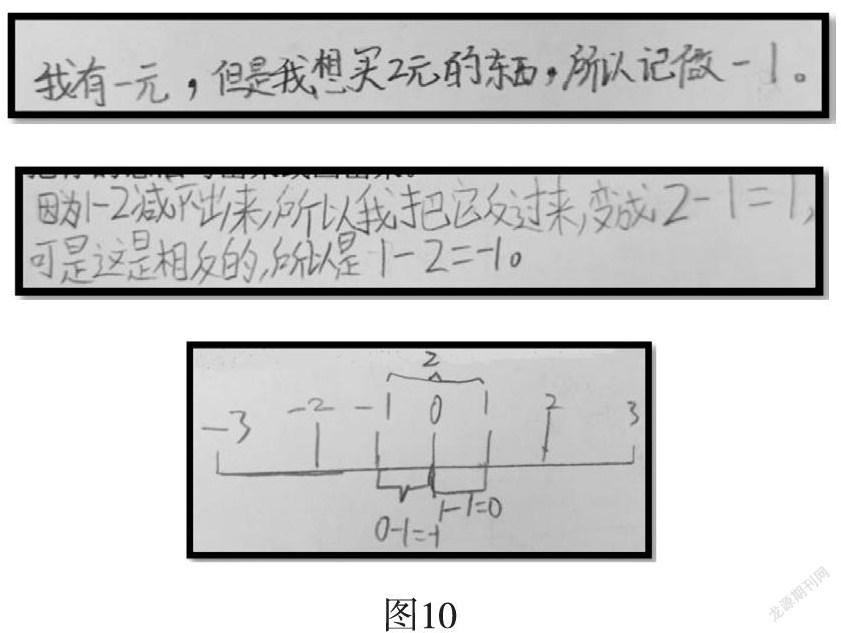
師：1-2的結果呢？你能寫一寫、畫一畫，讓大家了解你的想法嗎？

（學生獨立活動，展示學生作品如圖10，學生交流）

師：為什么計算1-2的時候你們想到了用負數來表示結果呢？

生：因為被減數減減數的時候不夠減了，所以我們想到用負數來表示。

師（小結）：人們在遇到小的數除以大的數，不夠除了的情況后，創造了分數;人們在遇到小的數減大的數，不好減了的情況后，創造了負數。

【評析】數的一個重要功能是能夠運算，新數的出現，常常受到運算的推動，比如“分數”的產生，原因之一就是基于整數除法運算的需要。這里教者利用一組算式，放手讓學生思考：1-2=？寫出你的想法，再進行全班交流。學生從運算角度體會引進負數的必要，以及負數在運算中表達的合理性，同時也為后續學習負數的四則運算、解方程等知識做鋪墊。

總評

認識負數是小學生數概念的又一次重要擴展。以前小學生學習的都是“算術數”，這些數與生活實際聯系緊密，學生感受和理解這些數的含義相對比較容易。學生雖然在日常生活中了解過負數，但在學生生活中直接應用負數的情況并不多見。因此，學生真正理解負數的概念還是存在一定困難的。為此，教者在深入研究教材的基礎上，對教學過程做了精心設計，體現了以下特色：

（1）改變單純由溫度計引入負數的做法，采用豐富多樣的事例，循序漸進地揭示負數是表示相反意義的量。“相反意義的量”通常有自然意義和人為規定意義兩種。輸與贏、收與支、盈與虧等都是自然意義下“相反意義的量”，學生易于理解;而溫度、海拔等都需要規定“0”點，具有“人造”的特點，相對復雜。因此，教者改由溫度計引入負數為從比賽的得分、扣分出發，讓學生初步感受具有相反意義的量是合適的。

（2）注重概括提煉，揭示負數概念的本質。概念是數學知識的細胞，是構成數學公式、規則、命題等規律性知識的基礎。學習數學概念，要讓學生盡可能了解概念從何而來，它的本質是什么，我們應該如何理解。教者通過生活中的負數、數軸上的負數、運算中的負數，層層遞進，逐步抽象，及時概括，不斷豐富負數的內涵，讓學生不僅認識到負數是具有相反意義的量，同時由于“0”的作用討論，讓負數的意義更加完整，負數與正數的關系更加清晰，通過對數的分類讓學生能更加清楚地認識到負數是一種新數。

（3）三個板塊步步深入，讓學生充分感受到負數來自多方面的需要，體驗到負數的價值。具體說來：

通過第一個板塊的學習，讓學生感受到負數是表示相反意義的量，運用負數能讓生活中問題的表達更加準確。

通過第二個板塊的學習，讓學生感受到負數在數軸上的排列、有理數的有序性，以及數的分類，讓學生對數的認識更加全面。

通過第三個板塊的學習，讓學生感受到有了負數能進行更多的運算，有利于解決更多的實際問題，也促進了數學科學的發展。

總之，本課創造性地運用教材，別具一格地對各個環節進行了精心設計，通過三個板塊的有序推進，讓學生對負數的本質及其規律有了清晰的認識，促進了學生數學思維的發展。