無人艇集群最優(yōu)協(xié)同控制反演

張振華, 李 堯, 俞成浦

無人艇集群最優(yōu)協(xié)同控制反演

張振華, 李 堯, 俞成浦*

(北京理工大學 自動化學院, 北京, 100081)

為實現(xiàn)通過數(shù)據(jù)驅動學習人為操作下的無人艇集群最優(yōu)協(xié)同控制策略, 文中提出了一種線性二次型閉環(huán)微分博弈反演優(yōu)化算法, 根據(jù)觀測到的系統(tǒng)最優(yōu)狀態(tài)和控制輸入軌跡辨識協(xié)同策略目標函數(shù)。首先, 根據(jù)觀測到的含加性白噪聲的最優(yōu)系統(tǒng)狀態(tài)和控制輸入軌跡辨識最優(yōu)反饋矩陣; 然后, 通過求解由納什平衡充要條件推出的耦合代數(shù)黎卡提方程的解來辨識協(xié)同策略目標函數(shù)。所提出的反演優(yōu)化算法能夠獲得滿足給定系統(tǒng)狀態(tài)和控制輸入軌跡的最優(yōu)協(xié)同策略目標函數(shù); 同時, 該算法辨識出的目標函數(shù)可以用于實現(xiàn)針對特定任務場景的無人艇集群最優(yōu)協(xié)同控制, 并為集群的對抗博弈提供新的思路和解決方案。

無人艇集群; 最優(yōu)協(xié)同控制; 反演優(yōu)化; 耦合代數(shù)黎卡提方程

0 引言

無人艇集群能在復雜海況下執(zhí)行協(xié)同任務, 其在軍用和民用領域的應用前景十分廣泛。針對給定的任務目標, 無人艇集群的理想行為可以看作是其最優(yōu)協(xié)同控制的結果[1-2]。在實際應用中, 實現(xiàn)最優(yōu)的協(xié)同控制必須有最優(yōu)的定量協(xié)同策略作為具體評價標準, 也就是無人艇集群在任務執(zhí)行期間的決策和行為應使某些目標函數(shù)的值達到最優(yōu)(一般是最小值)。由于無人艇集群工作環(huán)境的復雜性和拓撲連接的多樣性, 其最優(yōu)協(xié)同控制策略很難直接采用強化學習等方法試探[3]。一種快速得到最優(yōu)協(xié)同控制目標函數(shù)的思路是以“人”為最優(yōu)參考標準[4], 在某一任務場景下讓一組經(jīng)驗豐富的操作人員做出決策進而控制各個無人艇, 并采集無人艇集群的動態(tài)信息, 包括無人艇集群的運動狀態(tài)和每個操作人員對單艘無人艇的控制輸入。然后結合采集得到的動態(tài)信息和已知的無人艇集群動力學特性, 將人對各無人艇的控制策略反演優(yōu)化為機器可以理解的目標函數(shù)。使用反演優(yōu)化出的目標函數(shù), 無人艇集群可以在無人的任務場景中自主決策從而實現(xiàn)最優(yōu)協(xié)同控制。這種從行為信息和系統(tǒng)模型出發(fā)得到最優(yōu)協(xié)同控制策略的問題一般被稱為最優(yōu)協(xié)同控制反演問題。探究最優(yōu)協(xié)同控制反演問題對揭示人類操艇經(jīng)驗的隱性知識有很大幫助, 可推動無人艇集群最優(yōu)協(xié)同控制的研究。

作為無人艇集群最優(yōu)協(xié)同控制的參考對象, 人與人之間協(xié)同是在了解任務目標和他人當前情況條件下, 各自做出完成自身當前任務的最優(yōu)決策。為了使無人艇集群更好地模擬人的協(xié)同策略, 即通過辨識得到的模型自主產(chǎn)生的最優(yōu)協(xié)同控制策略與人遙控的策略盡可能吻合, 文中選用納什最優(yōu)下的微分博弈模型為辨識模型[5], 設計無人艇集群最優(yōu)協(xié)同控制反演算法來辨識各無人艇目標函數(shù)權重矩陣的參數(shù)值。由于絕大多數(shù)情況下各無人艇在協(xié)同過程中能同人一樣實時交換所需信息, 所以文中使用閉環(huán)微分博弈模型作為辨識模型。因而, 在算法研究中, 無人艇集群的最優(yōu)協(xié)同控制反演可以近似為無人艇集群的閉環(huán)納什最優(yōu)微分博弈反演優(yōu)化問題。

針對閉環(huán)非合作微分博弈反演問題, 國內外學者已經(jīng)進行了一些基礎性的研究[6-7]。Li等[8]研究了對應于穩(wěn)態(tài)納什策略的對稱耦合代數(shù)黎卡提方程, 所提出的并行算法收斂到耦合代數(shù)黎卡提方程的非負(正)定穩(wěn)定解; Priess等[9]提出了一套在連續(xù)時間和離散時間情況下尋找時不變線性二次調節(jié)器(linear quadratic regulator, LQR)問題的目標函數(shù)的技術, 并用于反演人體坐姿控制策略; Rothfu?等[10]以駕駛輔助系統(tǒng)為例, 研究了人機協(xié)同背景下如何通過非合作微分博弈反演對人的行為策略建模; Inga等[11]提出了一種方法來尋找在無限時間區(qū)間線性二次(linear quadratic, LQ)微分策略中產(chǎn)生相同納什平衡的所有成本函數(shù), 該方法依賴于耦合矩陣黎卡提方程的重新表述; Molloy等[12]提出了2種基于最小值原理的有限時間開環(huán)非線性微分博弈反演算法, 并在2個智能體三維避碰博弈實例中實現(xiàn)較高的辨識精度; K?pf等[13]設計了一種用于離散閉環(huán)博弈反演的方法, 并用于球-杠桿模型。

上述研究主要集中于理想博弈模型的反演, 但關于多人協(xié)同決策經(jīng)驗的建模與遷移應用還存在欠缺。無人艇集群的最優(yōu)協(xié)同控制反演問題主要體現(xiàn)在有3艘及以上目標函數(shù)未知的無人艇參與博弈, 且實際控制決策并非由理想博弈模型產(chǎn)生, 相當于采集的信號與參數(shù)逼近最好的理想模型得出的信號間存在固有噪聲。文中采用非合作閉環(huán)LQ納什最優(yōu)微分博弈模型, 給出了無人艇集群基于所反演優(yōu)化的模型參數(shù)自主實現(xiàn)最優(yōu)協(xié)同控制的決策方法, 即反演問題對應的正問題, 并將由該方法生成的軌跡加入噪聲以模擬人的實際決策過程, 然后基于約束優(yōu)化方法對無人艇集群的最優(yōu)協(xié)同控制反演過程進行數(shù)值仿真, 得到最接近實際協(xié)同控制過程的模型參數(shù), 分析其所反演模型生成的運動和控制軌跡與實際軌跡的誤差, 為今后基于無人艇集群最優(yōu)協(xié)同控制真實場景數(shù)據(jù)的反演與模型遷移研究提供參考。

1 模型建立

1.1 正問題求解

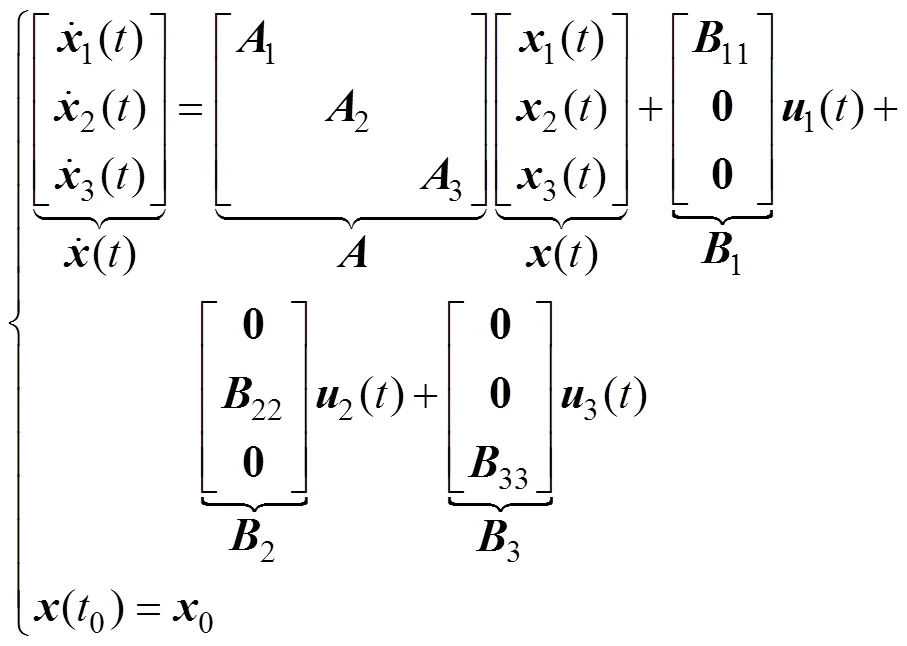
無人艇集群的最優(yōu)協(xié)同控制模型主要體現(xiàn)在最優(yōu)目標函數(shù)與系統(tǒng)動力學特性兩方面。為簡化計算并滿足實時性要求, 文中做出以下假設: 1)不考慮復雜海況和無人艇集群高時滯、大慣性、高度非線性等特征的影響, 無人艇集群系統(tǒng)動力學模型采用可鎮(zhèn)定線性時不變(linear time invariant, LTI)微分博弈系統(tǒng)模型; 2) 參考協(xié)同控制策略能夠采用參數(shù)適定的LQ閉環(huán)微分博弈目標函數(shù)模型近似; 3) 相同初始狀態(tài)下, 參考協(xié)同控制的系統(tǒng)狀態(tài)和控制輸入軌跡與由其反演得到的模型生成的軌跡之差用高斯白噪聲近似。

根據(jù)上述簡化與假設, 得到如式(1)所示無人艇集群系統(tǒng)方程來描述其運動特性

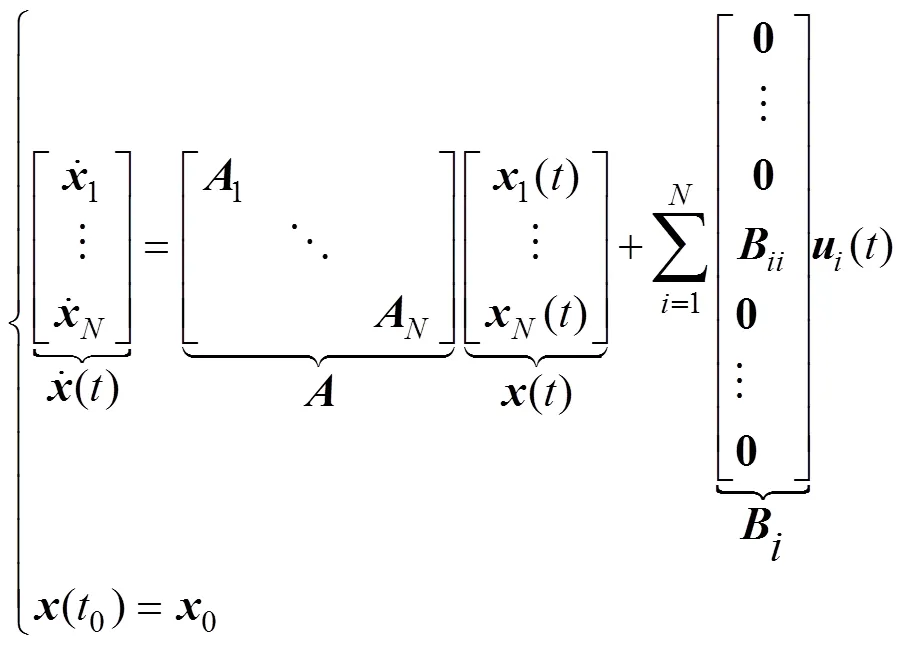
每艘無人艇的控制輸入與狀態(tài)間存在LTI反饋控制率, 即

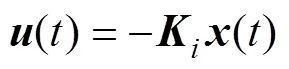
同時定義閉環(huán)系統(tǒng)矩陣

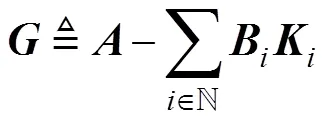
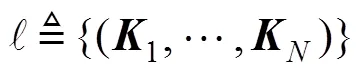
在如圖1所示的LQ非合作閉環(huán)微分博弈模型中, 每艘無人艇都力圖使自身的一個關于式(5)的目標函數(shù)

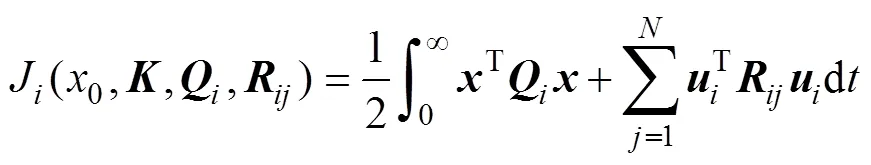
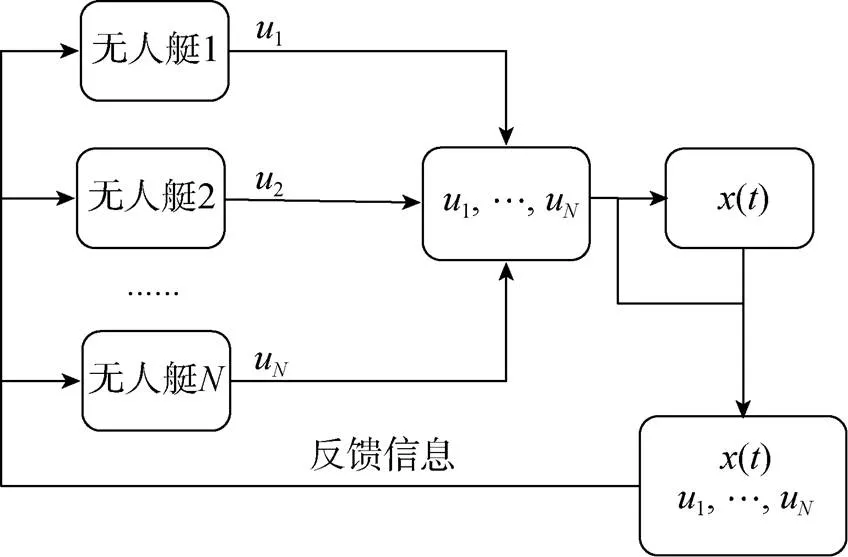
圖1 閉環(huán)微分博弈框圖

在上述模型中, 如果已知其他無人艇的控制率, 對于任意一艘無人艇, 都不能通過調整自身控制率來減小其目標函數(shù)值, 否則將被來自其他無人艇博弈性的調整反制, 達到平衡狀態(tài), 即

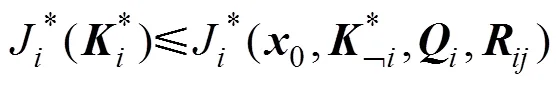
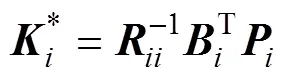
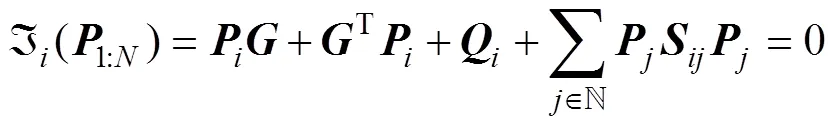
1.2 反演優(yōu)化算法

為了實現(xiàn)由采集到的無人艇集群運動狀態(tài)軌跡和每個操作人員對單艘無人艇的控制輸入反演, 優(yōu)化出無人艇集群最優(yōu)協(xié)同控制微分博弈模型, 此部分提出基于耦合黎卡提方程的反演優(yōu)化算法。

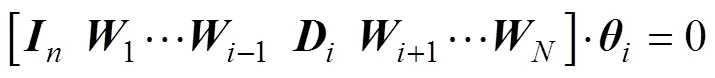
證明: 將式(8)向量化, 得到

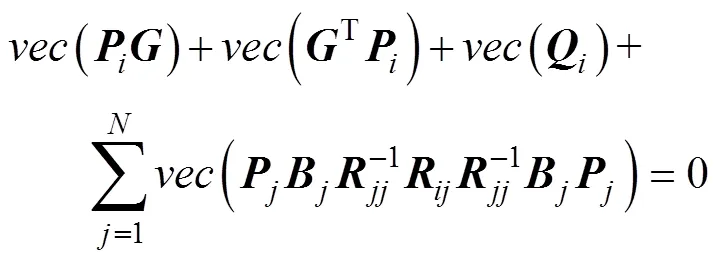
將式(7)代入上式并化簡得到

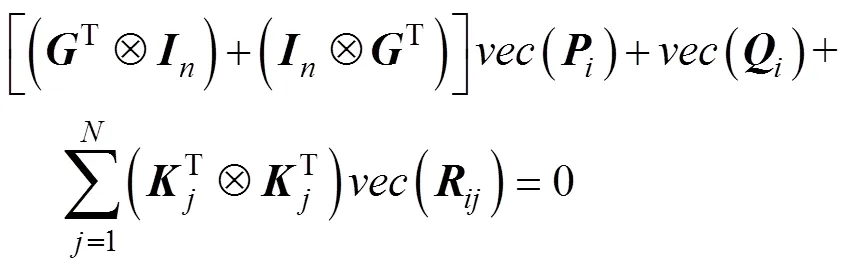
并將式(7)向量化得到

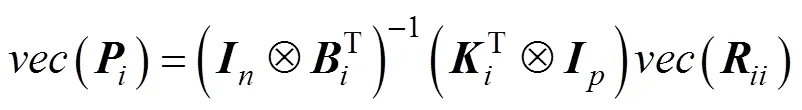
代入式(12)即可得到

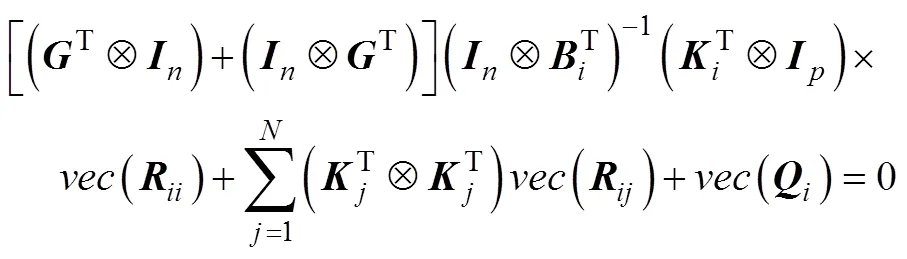
證明完畢。

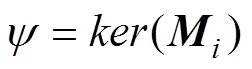
1) 目標函數(shù)權重矩陣為對稱矩陣

如果假設所有目標函數(shù)權重矩陣均為對稱矩陣, 則式(10)的未知參數(shù)個數(shù)為

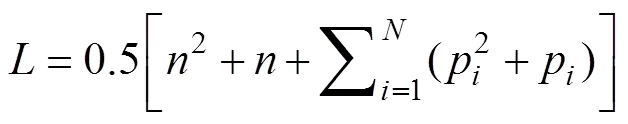
又因為

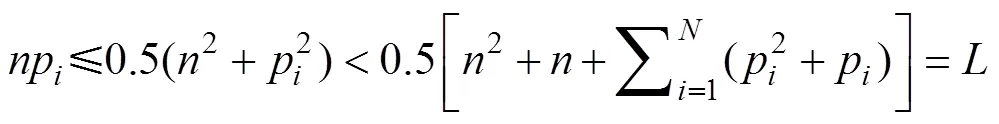
2) 目標函數(shù)權重矩陣為對角形式

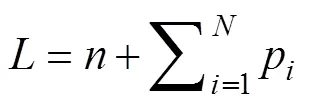
無人艇集群最優(yōu)協(xié)同控制反演優(yōu)化算法流程如下。

1) 建立采集到的納什平衡條件下無人艇集群運動狀態(tài)和每個操作人員對單艘無人艇的控制輸入信息模型

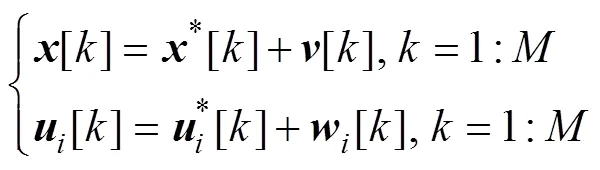
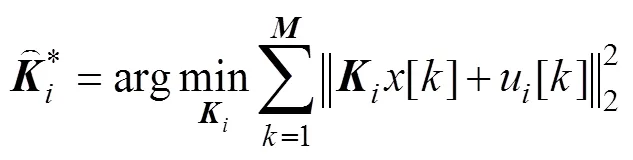
3) 建立反演優(yōu)化模型。根據(jù)式(2)、式(7)和式(19), 對無人艇集群最優(yōu)協(xié)同控制反演優(yōu)化問題建立如下優(yōu)化模型

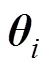
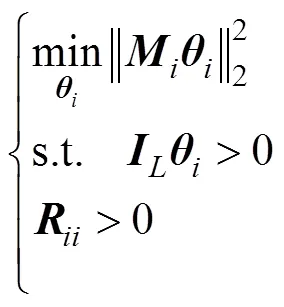
通過計算無人艇集群系統(tǒng)狀態(tài)真實值與預測值之間的相對誤差來驗證其準確性

2 仿真結果與分析

通過數(shù)值仿真驗證文中所提算法的有效性和準確性。

為了便于說明, 以圖2所示的3艘無人艇協(xié)同執(zhí)行補充補給任務(圖中: 中間為補給船; 三角形的3個頂點為執(zhí)行任務的無人艇)為例。將此3艘無人艇系統(tǒng)動態(tài)方程簡化為

用線性二次型微分博弈協(xié)同決策目標函數(shù)來近似無人艇執(zhí)行協(xié)同任務過程中的控制策略。然后通過采集在執(zhí)行協(xié)同任務過程中系統(tǒng)最優(yōu)狀態(tài)和各無人艇控制輸入軌跡辨識協(xié)同策略目標函數(shù)

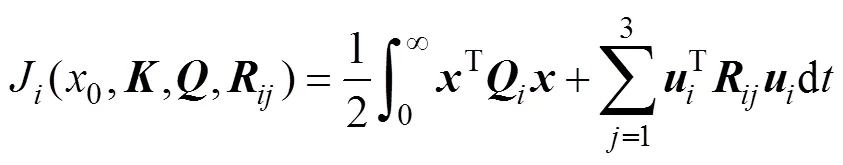
首先求解式(24), 并將得到的系統(tǒng)狀態(tài)和控制輸入軌跡作為觀測到的人為操作下無人艇集群系統(tǒng)最優(yōu)狀態(tài)和各無人艇最優(yōu)控制輸入。然后, 使用所求得的最優(yōu)狀態(tài)量和控制輸入量進行反演優(yōu)化。最后, 根據(jù)辨識得到的協(xié)同策略目標函數(shù)參數(shù)再次求解式(24), 得到系統(tǒng)狀態(tài)和各無人艇控制輸入軌跡, 并通過式(22)驗證算法的相對誤差水平。

現(xiàn)有文獻中并沒有能確保式(24)所表示的正向微分博弈問題一定收斂的算法, 因此在仿真中僅統(tǒng)計求解正向問題收斂的算法, 來驗證所提算法的有效性。

文中實例包含100組正向問題收斂情況下的數(shù)值試驗結果。所獲得的系統(tǒng)狀態(tài)預測相對誤差分布和統(tǒng)計直方圖分別如圖3和圖4所示。

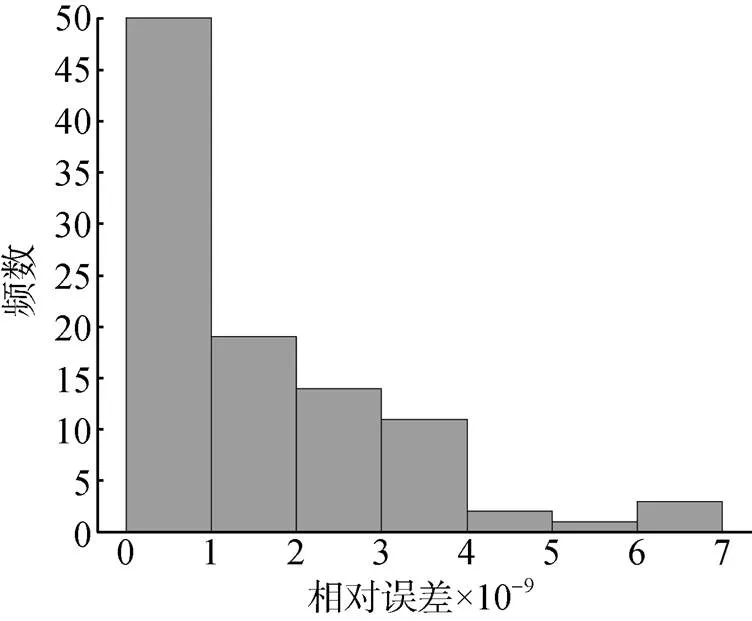
圖4 無噪聲條件下相對誤差統(tǒng)計直方圖

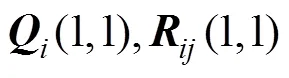
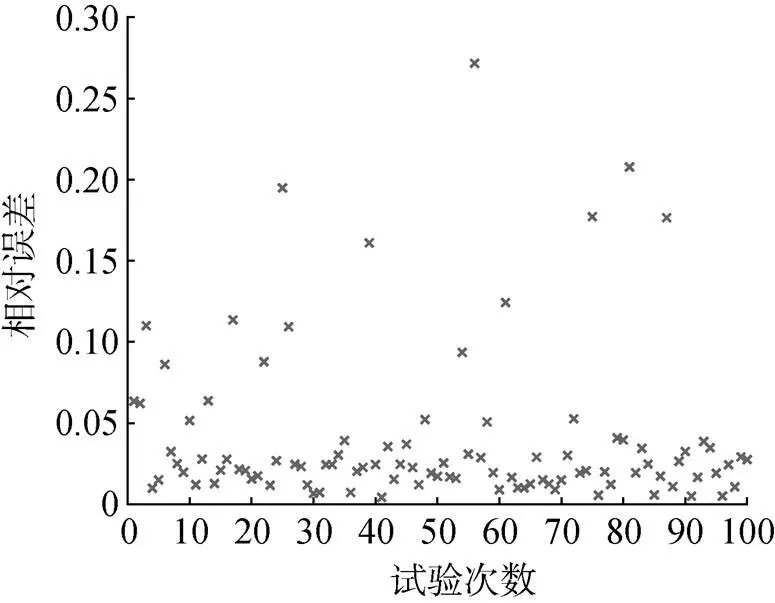
圖5 30 dB噪聲條件下相對誤差分布圖

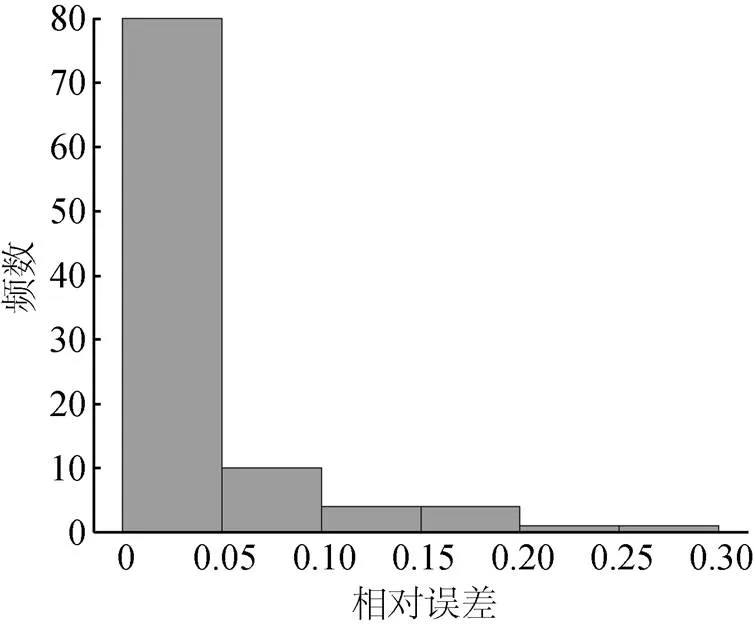
圖6 30 dB噪聲條件下相對誤差統(tǒng)計直方圖

3 結束語

文中提出了一種無人艇集群最優(yōu)協(xié)同控制反演優(yōu)化算法。該算法通過反演優(yōu)化線性二次型微分博弈問題的協(xié)同策略目標函數(shù)權重矩陣來學習無人艇集群最優(yōu)協(xié)同控制策略。此外, 該算法構建了一個雙層優(yōu)化的反演優(yōu)化模型, 并充分利用了線性二次型微分博弈問題達到納什平衡時的耦合代數(shù)黎卡提方程的性質, 將雙層優(yōu)化模型轉化為簡單的二次型規(guī)劃問題, 以實現(xiàn)快速求解。

文中所使用的無人艇集群系統(tǒng)方程是近似的線性方程, 且在噪聲干擾下反演優(yōu)化算法精度不高。后續(xù)要針對更符合實際的非線性系統(tǒng)方程展開無人艇集群的最優(yōu)協(xié)同控制反演優(yōu)化算法研究, 并提升算法的魯棒性。

[1] Carvalhosa S, Pedro Aguiar A, Pascoal A. Cooperative Motion Control of Multiple Autonomous Marine Vehicles: Collision Avoidance in Dynamic Environments[C]//Pro- ceedings of the 7th IFAC Symposium on Intelligent Autonomous Vehicles 2010. Lecce, Italy: IFAC, 2010: 282-287.

[2] Pedro Aguiar A, Almeida J, Bayat M, et al. Cooperative Control of Multiple Marine Vehicles: Theoretical Challenges and Practical Issues[C]//Proceedings of the 8th IFAC International Conference on Manoeuvring and Control of Marine Craft. Guarujá, Brazil: IFAC, 2009: 412- 417.

[3] Wang Y C, Fu H X, Liu F M. Ship Speed Control Method Based on Fuzzy-Cerebellar Model Articulation Controller[C]//Proceedings of the 31st Chinese Control Conference. Hefei, China: CCC, 2012: 4396-4399.

[4] Aza N A, Shahmansoorian A, Davoudi M. From Inverse Optimal Control to Inverse Reinforcement Learning: A Historical Review[J]. Annual Reviews in Control, 2020, 50: 119-138.

[5] Basar T, Olsder G J. Dynamic Noncooperative Game Theory[M]. London: Academic Press, 1999.

[6] Mohajerin Esfahani P, Shafieezadeh-Abadeh S, Hanasusanto G A, et al. Data-driven Inverse Optimization With Imperfect Information[J]. Mathematical Programming, 2018, 167(1): 191-234.

[7] Zhang H, Li Y, Hu X. Inverse Optimal Control for Finite-Horizon Discrete-time Linear Quadratic Regulator Under Noisy Output[C]//2019 IEEE 58th Conference on Decision and Control(CDC). Nice, France: IEEE, 2020.

[8] Li T Y, Gajic Z. Lyapunov Iterations for Solving Coupled Algebraic Riccati Equations of Nash Differential Games and Algebraic Riccati Equations of Zero-Sum Games[M]// New Trends in Dynamic Games and Applications. Boston: Birkh?user Boston Inc., 1995.

[9] Priess M C, Conway R, Choi J, et al. Solutions to the Inverse LQR Problem with Application to Biological Systems Analysis[J]. IEEE Transactions on Control Systems Technology, 2015, 23(2): 770-777.

[10] Rothfu? S, Inga J, K?pf F, et al. Inverse Optimal Control for Identification in Non-Cooperative Differential Games[J]. IFAC-Papers on Line, 2017, 50(1): 14909-14915.

[11] Inga J , Bischoff E , Molloy T L , et al. Solution Sets for Inverse Non-Cooperative Linear-Quadratic Differential Games[J]. IEEE Control Systems Letters, 2019, 3(4): 871- 876.

[12] Molloy T L, Inga J, Flad M, et al. Inverse Open-Loop Noncooperative Differential Games and Inverse Optimal Control[J]. IEEE Transactions on Automatic Control, 2019, 65(2): 897-904.

[13] K?pf F, Inga J, Rothfu? S, et al. Inverse Reinforcement Learning for Identification in Linear-Quadratic Dynamic Games[J]. IFAC-Papers on Line, 2017, 50(1): 14902- 14908.

Inverse Optimal Cooperative Control for Unmanned Surface Vessel Cluster

ZHANG Zhen-hua, LI Yao, YU Cheng-pu*

( School of Automation, Beijing Institute of Technology, Beijing 100081, China)

To realize an optimal cooperative control strategy of unmanned surface vessel(USV) clusters under artificial control through data-driven learning, a linear quadratic closed-loop differential game inverse optimization algorithm is proposed. The algorithm can identify the cooperative strategy objective function according to the optimal system state and control input trajectories. In this study, an optimal feedback matrix is first identified based on the observed optimal system state and control input trajectories with additive white noise. The cooperative strategy objective function is then identified after solving the coupled algebraic Riccati equations derived from the necessary and sufficient conditions for Nash equilibria.The proposed inverse optimization algorithm can obtain the optimal cooperative strategy objective function to satisfy the given system state and control input trajectories. The objective functions identified by the inverse optimization algorithm can then be used to achieve an optimal cooperative control of USV clusters for specific task scenarios and provide new ideas and solutions for cluster adversarial games.

unmanned surface vessel(USV) cluster; optimal cooperative control; inverse optimization; coupled algebraic Riccati equations

張振華, 李堯, 俞成浦. 無人艇集群最優(yōu)協(xié)同控制反演[J]. 水下無人系統(tǒng)學報, 2020, 28(6): 611-617.

TJ630; U664.82; TP273.1

A

2096-3920(2020)06-0611-07

10.11993/j.issn.2096-3920.2020.06.004

2020-09-04;

2020-10-16.

國家自然科學基金重大項目課題(61991414).

俞成浦(1984-), 男, 博士, 教授, 主要研究方向為系統(tǒng)辨識與機器學習、分布式優(yōu)化與控制、無線傳感器網(wǎng)絡與室內定位.

(責任編輯: 陳 曦)