指向深度學(xué)習(xí)的數(shù)學(xué)“問題鏈”設(shè)計
方偉 徐偉
摘要:探討如何遵從“問題鏈”教學(xué)的動機性、關(guān)聯(lián)性、思維性和多樣性等特點,運用“知識聯(lián)系”“數(shù)學(xué)活動” “題目變式”等策略進行“問題鏈”的設(shè)計與實施,開展有意義的深度學(xué)習(xí),為學(xué)生深入進行數(shù)學(xué)思考提供機會,進一步提升學(xué)生的數(shù)學(xué)能力與思維品質(zhì),發(fā)展數(shù)學(xué)核心素養(yǎng)。
關(guān)鍵詞:深度學(xué)習(xí);“問題鏈”;數(shù)學(xué)思考
一、問題引發(fā):無關(guān)聯(lián)的問題群和壓縮化的教學(xué)使學(xué)習(xí)普適性缺失
學(xué)生真實的學(xué)習(xí)歷程是緩慢而復(fù)雜的。與之形成鮮明對比的,我們的課堂教學(xué)過程卻是高速和極度壓縮的,具體表現(xiàn)為以下五個方面。
(1)從目標上看,較少考慮學(xué)生的需求,沒有深入分析學(xué)情,教師對知識打包壓縮,教給學(xué)生。
(2)從內(nèi)容上看,較少考慮學(xué)生的視角,且內(nèi)容龐雜、信息量大,不進行區(qū)分、篩選、歸納,造成重復(fù)、低效學(xué)習(xí),難以激發(fā)學(xué)生的學(xué)習(xí)興趣。
(3)從進度上看,學(xué)生跟不上教學(xué)進度,教學(xué)進度與學(xué)生進度有落差,積壓了難以完成的學(xué)習(xí)任務(wù)。
(4)從設(shè)計上看,較少從學(xué)生的學(xué)習(xí)角度進行“學(xué)習(xí)設(shè)計”,教師只從教學(xué)的角度進行“教學(xué)設(shè)計”。
(5)從方法上看,以教師講授為主,學(xué)生沒有自主思考和探究的過程,只是在被動地接受,學(xué)習(xí)無法深入,學(xué)生能力無法真正提升。
近年來,筆者積極探索嘗試設(shè)計一系列問題,通過“環(huán)環(huán)相扣,步步推進”的“問題鏈”教學(xué),引導(dǎo)學(xué)生探究知識本質(zhì),進入基于理解、遷移應(yīng)用的深度學(xué)習(xí)狀態(tài),促進課堂教學(xué)向?qū)W生深度學(xué)習(xí)的方向轉(zhuǎn)型。
二、變革方向:以問題鏈為腳手架的深度學(xué)習(xí)設(shè)計實踐
(一)深度學(xué)習(xí)的理念
深度學(xué)習(xí),就是在教師引領(lǐng)下,學(xué)生圍繞著具有挑戰(zhàn)性的學(xué)習(xí)主題,全身心積極參與、體驗成功、獲得發(fā)展的有意義的學(xué)習(xí)過程。通俗地說,就是在已有的經(jīng)驗和認知體系下,通過對知識的深層次理解,建立起一種內(nèi)在的、由此及彼的邏輯關(guān)聯(lián)。深度學(xué)習(xí)基于學(xué)生自發(fā)和自主性的學(xué)習(xí)動機,依靠學(xué)生對問題本身探究的內(nèi)在興趣,是一種長期的、全身心投入的持久學(xué)習(xí)力。
(二)“問題鏈”的內(nèi)涵
“問題鏈”通過獨立又關(guān)聯(lián)、具有系統(tǒng)性和層次性并層層推進的問題組驅(qū)動學(xué)生的數(shù)學(xué)思考,讓學(xué)生在問題解決中實現(xiàn)數(shù)學(xué)再創(chuàng)造,在再創(chuàng)造過程中建構(gòu)新知識、體驗數(shù)學(xué)思想方法。從形式上看,“問題鏈”是環(huán)環(huán)相扣的。從目標上看,它步步深入,將疑問和目標通過“鎖鏈”連在一起,通過一系列的設(shè)問,讓學(xué)生的思維得到碰撞、產(chǎn)生共鳴。
(三)“問題鏈”的設(shè)計原則
1.動機性
“問題鏈”的設(shè)計要盡可能激發(fā)學(xué)生的興趣和求知欲。教師要充分考慮學(xué)生的最近發(fā)展區(qū),編排富有感性體驗和趣味性的問題組,并創(chuàng)設(shè)真實的問題情境,營造積極的數(shù)學(xué)文化,將學(xué)生真正帶入有意義的數(shù)學(xué)學(xué)習(xí)活動中來。
2.關(guān)聯(lián)性
“問題鏈”的設(shè)計強調(diào)為學(xué)生提供數(shù)學(xué)思考的基本脈絡(luò),倡導(dǎo)讓學(xué)生在思維脈絡(luò)中產(chǎn)生問題、研究問題。數(shù)學(xué)知識和方法之間的關(guān)聯(lián)成為數(shù)學(xué)“問題鏈”設(shè)計的邏輯起點。“問題鏈”設(shè)計的關(guān)聯(lián)有效能夠幫助學(xué)生建立起良好的認知結(jié)構(gòu),有助于學(xué)生實現(xiàn)知識與方法的遷移。教師要根據(jù)學(xué)生的學(xué)習(xí)現(xiàn)實與學(xué)習(xí)需求選擇合適的關(guān)聯(lián)在“問題鏈”設(shè)計中加以應(yīng)用。
3.思維性
在教學(xué)中經(jīng)常有這樣的現(xiàn)象:教師問的問題過于直接,問題與問題之間跨度較小,限制了學(xué)生數(shù)學(xué)思考的空間。在“問題鏈”中,問題與問題之間的關(guān)聯(lián)與跨度為學(xué)生進行多元思維與探索提供了可能。“問題鏈”中的各問題之間應(yīng)該體現(xiàn)基本的思維方法,以便學(xué)生經(jīng)歷像數(shù)學(xué)家一樣的思考過程,在思考過程中培養(yǎng)學(xué)生基本的數(shù)學(xué)思維,將學(xué)生的數(shù)學(xué)思考逐漸引向深入,從而使學(xué)生獲得較高認知水平的數(shù)學(xué)能力。
4.多樣性
由于數(shù)學(xué)內(nèi)容類型的多樣性及教育目標的豐富性,具有適切的內(nèi)容特征及目標特征的“問題鏈”也是多樣的。“問題鏈”設(shè)計要杜絕單一和僵化,多根據(jù)不同特點的教學(xué)內(nèi)容,采用不同類型的“問題鏈”,促進學(xué)生對數(shù)學(xué)的深度學(xué)習(xí)。
三、實施路徑:基于“問題鏈”的深度學(xué)習(xí)探究
(一)實施“問題鏈”教學(xué)的具體策略
1.“知識聯(lián)系”策略——利用新舊知識之間的聯(lián)系設(shè)計“問題鏈”
在教學(xué)過程中,若能將新舊概念間的聯(lián)系點設(shè)計成“問題鏈”,通過對“問題鏈”的回答,引導(dǎo)學(xué)生建立起新舊知識間的聯(lián)系,在新知識有生長的根基、舊知識有延伸的活力的基礎(chǔ)上猜想并驗證,就可以使學(xué)生比較容易地掌握新知識。
例如,在教學(xué)浙教版八年級下冊的“正方形的定義”后,筆者設(shè)置了以下3個問題。
問題1:正方形有哪些性質(zhì)?
問題2:哪些圖形的性質(zhì)正方形都具有?
問題3:正方形具有而一般矩形和菱形不具有的性質(zhì)有哪些?
這3個問題,層層遞進,讓學(xué)生感受到新舊知識的變化和聯(lián)系,將零散的、割裂的知識在頭腦中建構(gòu)起一條知識鏈,生長出縱橫連通的“知識樹”,構(gòu)建起知識之間的深度聯(lián)系,使數(shù)學(xué)知識結(jié)構(gòu)化完善。
2.“數(shù)學(xué)活動”策略——利用數(shù)學(xué)活動設(shè)計“問題鏈”
通過動手操作、觀察、猜想、分析而進行的數(shù)學(xué)活動,也指根據(jù)常識和已有經(jīng)驗,通過合情推理、假設(shè)與證明而進行思維實驗。以數(shù)學(xué)實驗為切入點設(shè)計的“問題鏈”,以完善學(xué)習(xí)者的經(jīng)驗結(jié)構(gòu)為基礎(chǔ),在由直觀感受上升為理性分析的過程中,提高學(xué)習(xí)效率。
3.“題目變式”策略——利用題目變式設(shè)計“問題鏈”
通過改變問題的條件、結(jié)論或轉(zhuǎn)換問題的形式或內(nèi)容來設(shè)計“‘問題鏈變式”。如果問題難度比較大,讓學(xué)生無法承受,就必須插入問題組形成“問題鏈”,以減少問題和問題之間的思維跨度,形成“‘問題鏈變式”。
(二)基于“問題鏈”的深度學(xué)習(xí)教學(xué)案例設(shè)計
現(xiàn)以浙教版七年級上冊“3.2實數(shù)”為例,闡述筆者基于“問題鏈”的深度學(xué)習(xí)設(shè)計理念。
1.教學(xué)聯(lián)結(jié)點
在實數(shù)的內(nèi)容教學(xué)之前,學(xué)生對有理數(shù)的概念和運算已有了深刻的理解和掌握,根據(jù)數(shù)的擴充一致性,類比有理數(shù)概念(如相反數(shù)、絕對值)和運算(法則、性質(zhì)、運算律)來進行實數(shù)的學(xué)習(xí),以此給出實數(shù)的概念與分類。
2.“問題鏈”的設(shè)計
開場白:科學(xué)家對數(shù)的研究,經(jīng)歷了漫長的歷程。自然數(shù)幫我們解決了計數(shù)的問題。進入初中階段,我們引入正負數(shù)和數(shù)軸的概念,得到了新的整數(shù)和有理數(shù)概念。
問題1:現(xiàn)在我們對整數(shù)可以怎么分類?
問題2:我們?nèi)绾伪硎痉謹?shù)?
問題3:有理數(shù)如何進行數(shù)學(xué)表示?
通過這3個問題,讓學(xué)生回顧已有知識,感受從自然數(shù)到整數(shù)再到有理數(shù)的擴充過程,感受數(shù)的擴充是因為數(shù)學(xué)自身發(fā)展的需要,系統(tǒng)建構(gòu)、復(fù)習(xí)有理數(shù)的有關(guān)知識。
問題4:有理數(shù)都可以表示成 ?(p、q為整數(shù),p、q互質(zhì),且p不為0)的形式嗎?有沒有特殊形式?
問題5:學(xué)校美術(shù)創(chuàng)意比賽要求作品的尺寸不能大于30平方分米 ,小明的參賽作品是一塊邊長為5.4分米的正方形畫布。
小明的作品大小符合要求嗎?這個問題的實質(zhì)是什么?運用了哪種運算?
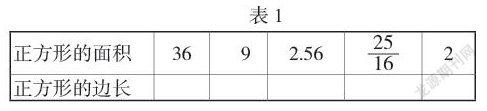
穿插活動,填寫下表(如表1所示)。
問題6:如果知道正方形的面積,我們能夠求得正方形的邊長嗎?如果正方形的面積為2,邊長是多少?
明確問題的實質(zhì)是“已知一個正數(shù),求其平方根”,是乘方的逆運算,為接下來的學(xué)習(xí)做鋪墊。4個問題組成的“問題鏈”,引發(fā)學(xué)生對現(xiàn)有有理數(shù)不足以解決面積問題產(chǎn)生思考,讓學(xué)生強烈感受到有理數(shù)的局限性,認識到還存在我們不了解、不知道的一類數(shù)。
3.基于“問題鏈”的深度學(xué)習(xí)案例反思
(1)追求概念性理解。對“面積為2的正方形的邊長到底有多大”這個問題展開研究,感知這樣不是整數(shù)、也不是分數(shù)的“非有理數(shù)”的存在;用無限逼近法進行估算,感知不是有理數(shù),讓學(xué)生真正理解無理數(shù)。
(2)指向知識結(jié)構(gòu)化。實數(shù)教學(xué)基于學(xué)生已有知識的最近發(fā)展區(qū),從已學(xué)的整數(shù)和有理數(shù)著手,梳理已學(xué)知識,為后續(xù)類比進行鋪墊,融入以往經(jīng)驗,讓教學(xué)得以提升并形成結(jié)構(gòu)。
(3)發(fā)展高階思維。為了讓學(xué)生探討 到底有多大,筆者設(shè)計了二分法的估算,此舉既為探索數(shù)學(xué)規(guī)律活動,也為培養(yǎng)學(xué)生洞察事物本質(zhì)的能力。學(xué)生經(jīng)歷了對數(shù)據(jù)的理解和算法的合理選擇,以及對結(jié)果的正確判斷,提高了邏輯推理能力,優(yōu)化了自己的高階思維品質(zhì)。
四、學(xué)習(xí)深化:有品質(zhì)的“問題鏈”設(shè)計促進深度學(xué)習(xí)
在基于“問題鏈”的深度教學(xué)中,筆者力求“彈性設(shè)計與動態(tài)生成”“學(xué)生能力和素養(yǎng)培養(yǎng)”的和諧統(tǒng)一,一年來積累了一些經(jīng)驗,學(xué)生學(xué)習(xí)高效了、思維有了深度。
(一)深度課堂——重探究,重思維
“問題鏈”教學(xué)促進學(xué)生對數(shù)學(xué)的深度理解,并實現(xiàn)深度學(xué)習(xí)目標。“問題鏈”教學(xué)有利于學(xué)生開展探究性學(xué)習(xí)活動,驅(qū)動學(xué)生的思考,給學(xué)生提供深入思考與探索的空間,喚醒學(xué)生的思維意識,引領(lǐng)學(xué)生進入高階思維。
(二)改變學(xué)力——善發(fā)現(xiàn),善提問
“問題鏈”構(gòu)建了教師“教”和學(xué)生“學(xué)”之間的紐帶。學(xué)生通過發(fā)現(xiàn)問題、猜想探究、驗證說明、再提出新的問題,不斷地發(fā)現(xiàn)問題、提出問題、解決問題,主動探究新知,自主學(xué)習(xí)能力不斷得到提升。
(三)提升素養(yǎng)——會整理,會反思
“問題鏈”數(shù)學(xué)課堂教學(xué)嘗試是整合性學(xué)習(xí)的一種回歸,學(xué)生會梳理知識的內(nèi)在聯(lián)系與本質(zhì),反思如何用聯(lián)想、結(jié)構(gòu)的方式去學(xué)習(xí),豐富和完善原有的認知結(jié)構(gòu)。
基于“問題鏈”的深度學(xué)習(xí),轉(zhuǎn)變了教師的教學(xué)觀念,讓學(xué)生的學(xué)習(xí)真實地發(fā)生,將課堂學(xué)習(xí)推向更深層次的理解性學(xué)習(xí)。
參考文獻:
[1]劉月霞,郭華. 深度學(xué)習(xí):走向核心素養(yǎng)(理論普及讀本)[M].北京:教學(xué)科學(xué)出版社,2018.
[2]唐永.指向深度學(xué)習(xí)的數(shù)學(xué)課堂“追問”設(shè)計[J].教學(xué)月刊,2020(11).
[3]徐曉燕.概念性理解與數(shù)學(xué)概念教學(xué):基于數(shù)學(xué)任務(wù)設(shè)計的視角[M].上海:上海教育出版社,2020.
(責(zé)任編輯:奚春皓)

