小學高段學生數感水平測試問卷編制研究

趙雨晴 吳敏霞 鞏子坤

【摘? ?要】數感是重要的數學核心概念，是小學數學教學中應重點關注的內容之一。基于相關成果、專家意見和學生特點，編制了評估小學4～6年級學生數感水平的問卷。通過兩次大規模樣本測試，采用探索性因素分析、驗證性因素分析等方法，對問卷題目進行修訂。最終形成的問卷包含數的意義、數的大小、數與運算、數與估計四個維度。該問卷的信效度良好，可以作為評估小學4～6年級學生數感水平的有效工具。

【關鍵詞】4～6年級學生;數感;問卷編制

一、引言

Tobias Dantzig 在1954年首次提出“數感”（Number sense）這一概念，他認為數感是對微小數量變化的一種直覺感受[1]。2001年，我國在《全日制義務教育數學課程標準（實驗稿）》中首次明確提出要培養兒童的數感，隨后在《義務教育數學課程標準（2011年版）》中將數感列為十大核心概念之一。由此，數感的內涵、發展規律和培養方法等逐漸成為研究的熱點[2-3]。全面考察小學生數感水平的發展特點及其影響因素，可以為小學生數感的培養提供指導。

近年來，針對如何培養學生數感而開展的研究數不勝數，許多數學教育學者都嘗試建立有效的測評方法以了解兒童的數感發展，并將其作為一個重要研究方向[4]。Clements[5]、Griffin等人[6]、Malofeeva等人[7]基于兒童數感發展理論設計量表，測評學前以及特定年齡兒童的數感發展狀況。張樹東等[8]研究4～6歲兒童的數感特點，張麗錦等[9]對一年級兒童的數感展開研究。

本研究基于已有文獻，對數感內涵進行再認識，確定其維度并給出操作性定義;編制問卷對學生進行測試，征求專家意見后修改問卷，再次進行大規模樣本測試，通過對收集到的數據進行分析，最終形成一套“小學4～6年級數感水平調查問卷”。

二、問卷編制過程與方法

（一）問卷維度及其操作性定義

Sowder[10]認為，有數感的人應當能較好地連接數與運算的概念;能利用數的相對與絕對大小比較數的大小;能以估算的形式判斷結果的合理性;掌握心算的方法。馬云鵬、史炳星[11]認為，在中小學數學教學中，數感主要是指學生具有應用數字表示具體數據和數量關系的能力;具有選擇適當的方法進行計算的經驗;能依據數據進行推論，并對數據和推論的精確性和可靠性進行檢驗。數學教育工作者Der-Ching Yang對數感的組成成分進行了如下分類：理解數的意義;辨別數的相對大小;恰當地運用基準量;理解運算對數的影響;恰當運用不同的解題策略得出結果，并能判斷結果的合理性。

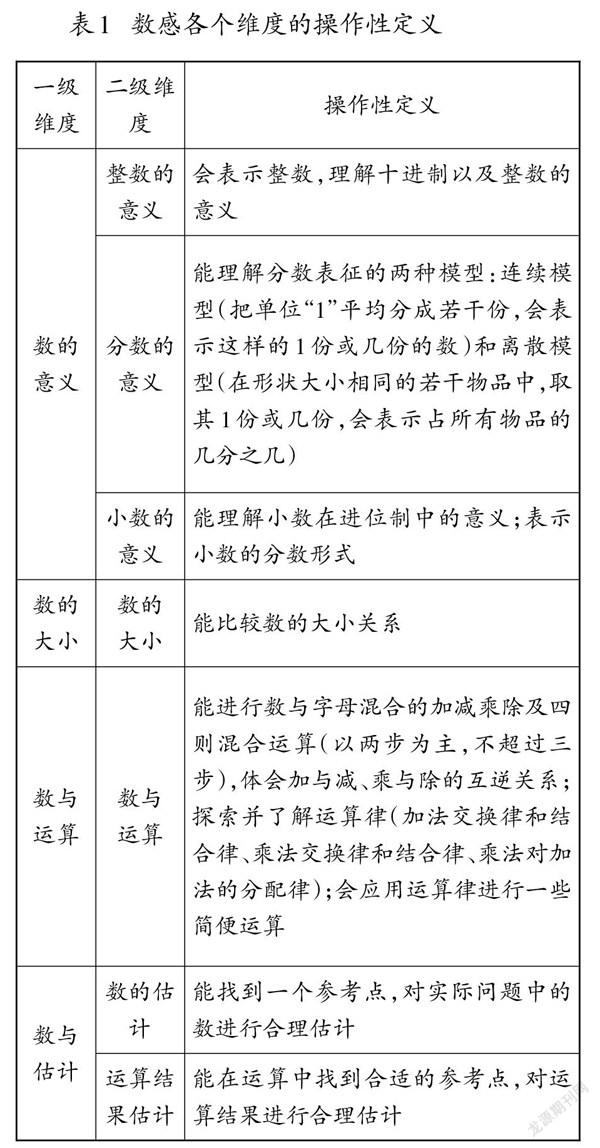
由此可見，目前數學教育領域普遍認為“數感”是對數的概念、數與運算、數字關系和數字模式的理解，以及運用數學知識解決問題的能力。結合以往研究和課標要求，進行文獻梳理后，與數學教育專家及小學優秀教研員多次探討小學階段數感的內涵，歸納出以下四個重要維度：數的意義、數的大小、數與運算、數與估計。由此，建構了數感的維度以及各個維度的含義和操作性定義（如表1）。

（二）問卷題目的建立

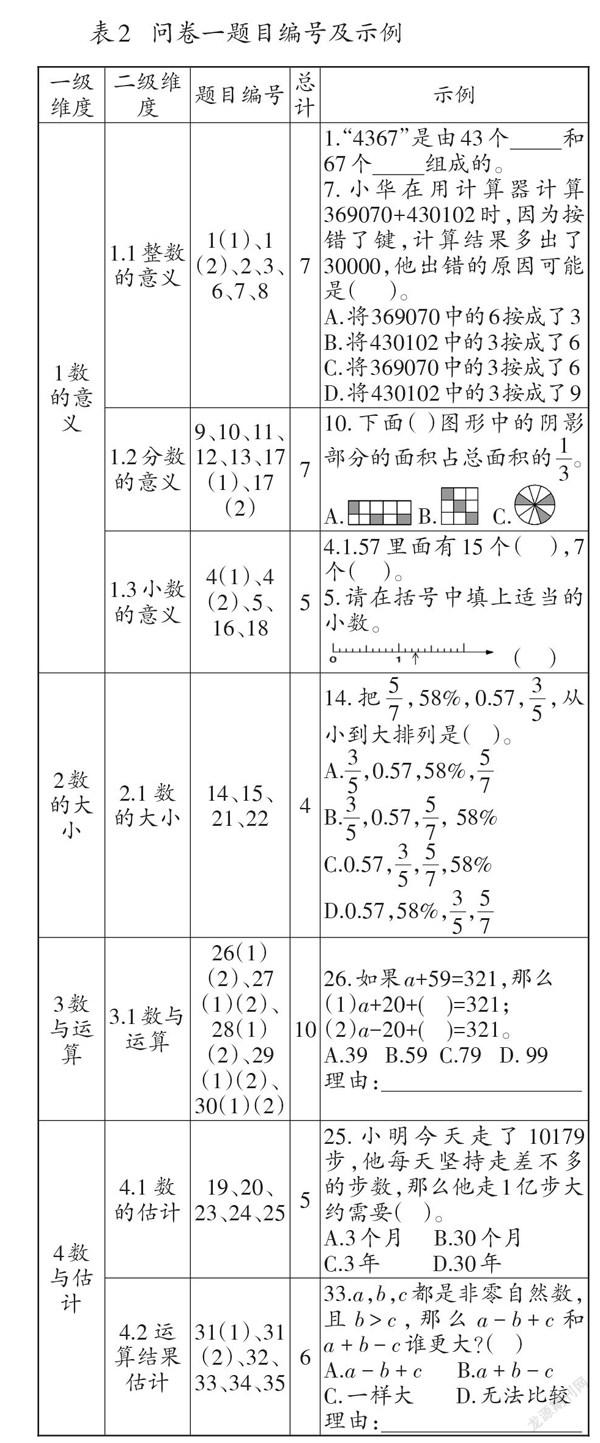
根據問卷題目編制的注意事項[12-14]，分析每份問卷的題項。考慮到小學4～6年級學生相比低段學生，在思維方式方面出現了較大變化，形象思維開始向抽象思維和邏輯思維過渡[15]，并且已經學習了用字母表示數，因此改編現有問卷題目時，以字母代替圖形符號，形成了含有44道題目的初始問卷（記為問卷一，見表2）。題型均為選擇題和填空題，每空記為1題（如第1題，該填空題有2空，記為2題），另外數與運算和運算結果估計的題目還需學生填寫選擇的理由。

（三）被試選取與問卷回收

整個問卷的編制過程一共進行了三次測試，測試后的分析以及問卷修訂詳見下文“預調查問卷的分析與修訂”。第一次發放問卷（問卷一）的對象為杭州市G區某小學五年級學生4人，測試后對學生進行訪談，了解學生對題目的理解情況。

第二次發放問卷（問卷二）用于問卷修訂過程中的探索性因素分析。選取杭州市X區某小學的四、五、六年級學生作為樣本，總樣本量為385人，回收有效問卷377份，有效率為97.9%。

第三次發放問卷（問卷三，見附錄）用于問卷修訂過程中的驗證性因素分析。選取杭州市G區某小學的四、五、六年級學生作為樣本，總樣本量為442人，回收有效問卷434份，有效率為98.2%。

（四）數據分析

問卷中每題正確記1分，錯誤記0分。另外數與運算以及運算結果估計的題目需要填寫選擇的理由，答案正確但理由不合理記為1分，答案正確且理由合理記為2分，其余情況記為0分。利用 SPSS 22.0對數據進行項目分析、相關分析、探索性因素分析，利用 AMOS 24.0 對數據進行驗證性因素分析。

三、預調查問卷的分析與修訂

（一）問卷試測

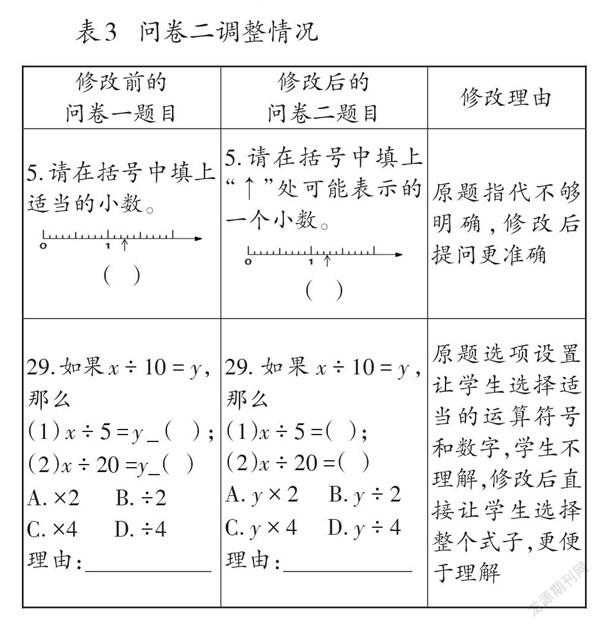
第一次測試（問卷一）的目的是避免學生因生字生詞而讀不懂題目，導致無法作答或作答錯誤。測試后通過訪談了解學生對題目的理解情況，在不改變題意的情況下，為便于學生理解，修改了其中3題的提問方式（詳見表3），并將問卷中出現的所有圖按順序進行編號，形成問卷二。

（二）項目分析

第二次測試（問卷二）后，回收問卷，錄入數據。

采用相關系數法，考察問卷中每道題與總分的相關性，最終發現，每道題目與總分均相關。采用臨界比率法（CR）對被測學生的得分進行差異性檢驗[16]，即計算每份問卷總分后，按總分從高到低排序，前27%（102人）為高分組，后27%（102人）為低分組，對兩組進行獨立樣本t檢驗，刪除不具有高低分組顯著性差異的2道題目（第3、12題）。

3.在五位數35698中，減去5個千后，得到的數是_____。

12.下圖中，涂顏色的圓占了全部圓的（? ? ?）。

A.[46]? ? ? B.[610]? ? ? ?C.[410]? ? ? D.[64]

（三）探索性因素分析

基于項目分析，對數據進行探索性因素分析。首先對問卷結構進行檢驗，發現問卷的KMO值為0.868，Bartlett球形度檢驗顯著（p=0.000<0.05），表明適合做因子分析。選擇主成分分析法和最大方差旋轉法進行分析，檢驗問卷維度以及相應題目。篩選問卷中的題目時主要遵循如下原則[17]：（1）保留因子特征值大于1的題目;（2）保留因子載荷值至少在0.4以上的題目;（3）刪除在兩個以及兩個以上的因子載荷值均大于0.4的題目。最后共計刪除21道題目（詳見表4），保留23道題目。

在探索性因素分析后，問卷的7個二級維度作為主成分被保留，但是其中“1.2分數的意義”和“2.1數的大小”只剩2題，按照問卷編制要求，每個子維度下至少包含3題，因此在這兩個維度下各修訂1題（見附錄第6題，第9題），形成問卷三，共25題（詳見表4與附錄）。

四、問卷的檢驗

（一）驗證性因素分析

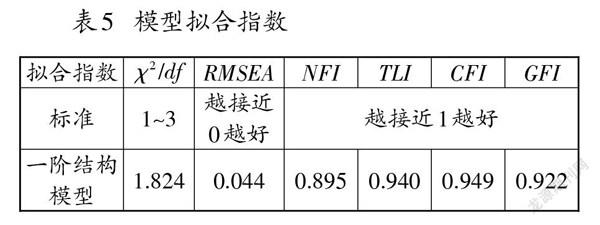
第三次測試（問卷三）后，回收問卷，錄入數據，對數據進行驗證性因素分析，檢驗實際數據模型與理論模型的擬合程度，如表5所示[18]。

第一步，進行一階兩兩相關模型驗證因素分析。根據分析結果，通過殘差進行修正，綜合考慮各項指標，一階因子的模型擬合程度較好，一階因子概念之間存在高度相關性，可進行下一步[19]。

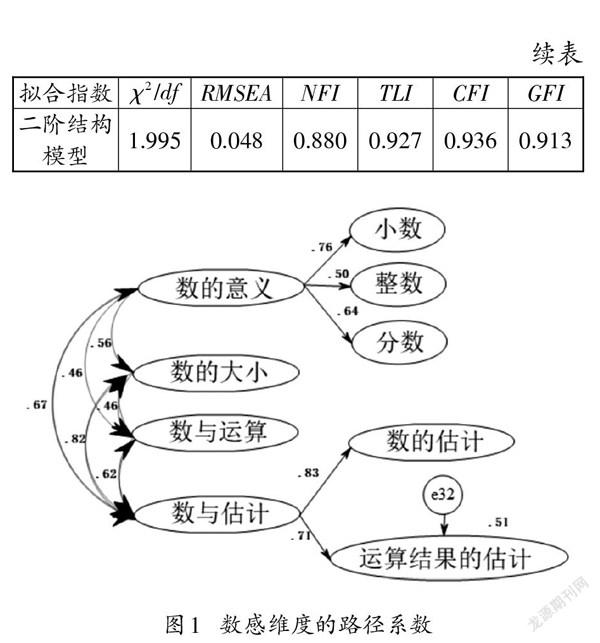
第二步，進行二階兩兩相關模型驗證因素分析。評價指標同第一步，綜合考慮各項指標，模型擬合程度較好。最終的維度路徑系數見圖1。

（二）問卷的信度和效度分析

1.信度分析

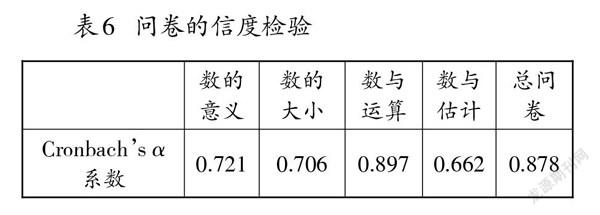
為了評估問卷的一致性、可靠性和有效性，采用Cronbach’s [α]系數計算問卷的內部一致性，對問卷進行信度檢驗。分別計算數的意義、數的大小、數與運算、數與估計4個維度以及總問卷的內部一致性信度（[α]系數），各項指標均達到標準（見表6），表明問卷的信度良好。

2.效度分析

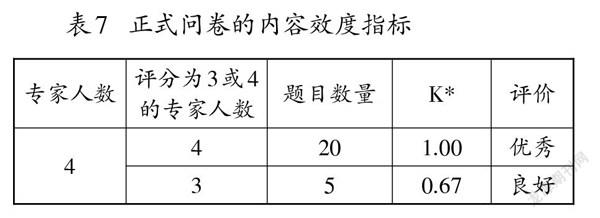
（1）內容效度：檢驗問卷實際測試的內容與所要測試內容之間的吻合程度[20]。目前，應用最廣泛的指標是內容效度指數（CVI）[21]。在問卷形成后，邀請4位專家（2位高校教師，2位教研員）對問卷題目與相應維度的關聯性進行打分。采用4等級評分：1=不相關，2=弱相關，3=較強相關，4=非常相關。打分完成后計算Kappa值（K*，0.60～0.74 為良好，大于 0.74 為優秀），結果如表7所示。

進一步計算問卷的內容效度值（S-CVI），結果顯示S-CVI/UA（被所有專家均評為3分或4分的題項數量占全部題項數量的百分比）為 0.80，S-CVI/Ave（問卷所有條目I-CVI的平均數）為 0.95。根據S-CVI/UA不低于 0.80，S-CVI/Ave應達到0.90的標準，本問卷的內容效度達到標準。

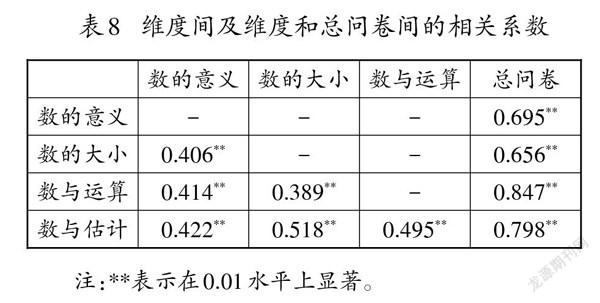
（2）結構效度：以驗證性因素分析的結果和問卷各維度間、各維度與總問卷間的相關系數作為檢驗指標[22]。在二階模型擬合指數中，[RMSEA]的值小于0.05，[TLI]與[CFI]的值大于0.9，這時擬合的模型是一個“好模型”[23]，結構效度達到要求。問卷各維度間、各維度與總問卷間的相關系數如表8所示，各維度之間存在著顯著的中度相關，相關系數在 0.389～0.518之間，各維度與總問卷之間存在中高度顯著相關，相關系數在0.656～0.847之間。分析表明，問卷所確立的4個一級維度之間有相對獨立性，各個維度與問卷整體相關性較大，因而問卷的結構效度較好。

五、討論

本次編制的“小學4～6年級數感水平調查問卷”在維度上沿用了研究者先前編制的“小學1年級數感水平調查問卷”[24]和“小學2-3年級數感水平調查問卷”[25]，但相比之下，本次問卷編制過程更嚴謹，具有科學性，主要體現在以下方面。

（一）大樣本選取

本次問卷編制過程中進行探索性、驗證性因素分析時選取的樣本量均在400人左右，流程為：基于對大樣本數據的探索性因素分析，對問卷進行修訂;再進行大樣本測試，對問卷進行驗證性因素分析。

（二）問卷編制過程具有嚴謹性、科學性

本次問卷編制過程共進行三次測試。初始問卷包含44道題目，先經過試測，修改了2道題的提問方式，保證學生在測試過程中不會因為不理解題意而發生錯誤。第二次大規模測試后對結果進行項目分析和探索性因素分析，修訂題目，形成結構合理的最終版本測試問卷，共包含25道題目。為了檢驗最終問卷的信度和效度，進行第三次大規模測試，對數據結果進行驗證性因素分析和信效度檢驗。本次問卷編制過程參照王光明等[26]編制問卷的方法，具有嚴謹性、科學性。

（三）問卷題目設計合理，結構完整，一脈相承

針對小學生數感的發展與特征，郭民[27]依據數感階段的劃分以及數感的構成要素設計了一套問卷用于測試2～6年級的所有學生，而本研究依據小學1～6年級學生的不同水平，設計了三套問卷。“小學1年級數感水平調查問卷”包括數字運算、數字意義、數字表示、數字關系、數字估計、問題情境六個維度，而“小學2～3年級數感水平調查問卷”在維度上有所調整。經過探索性因素分析，確定問卷結構包括數的意義、數的大小、數與運算、數與估計四個維度，因此“小學4～6年級數感水平調查問卷”沿用了這四個維度，使系列問卷一脈相承，具有系統性。本問卷含25道題目，數量合理，學生能在一課時內完成。

六、結論

“小學4～6年級數感水平調查問卷”的編制過程具有嚴謹性、科學性，問卷具有良好的信效度，可作為評估4～6年級小學生數感水平的有效工具。

參考文獻：

[1] DANTZIG T.Number： The language of science[M].New York： Macmillan，1954：4-5.

[2] 鄭婷.數感的內涵、價值與培養策略[J].小學數學教育，2019（10）：20-22.

[3] 周衛. 小學階段數感培養的策略研究[D].上海：上海師范大學，2012.

[4]趙振國.3～6歲兒童數感發展的研究[J].心理發展與教育，2008（4）：8-12.

[5]CLEMENTS D H. Training effects on the development and generalization of Piagetian logical operations and knowledge of number[J]. Journal of Educational Psychology， 1984， 76（5）：766-776.

[6]GRIFFIN S A， CASE R， SIEGLER R S. Rightstart： Providing the central conceptual prerequisites for first formal learning of arithmetic to students at risk for school failure[J]. Classroom lesson：Integrating cognitive theory and classroom practice， 1994：25-49.

[7]MALOFEEVA E ， DAY J ， SACO X ， et al. Construction and Evaluation of a Number Sense Test With Head Start Children[J]. Journal of Educational Psychology， 2004， 96（4）：648-659.

[8]張樹東，夏學楠，張文秀.4～6歲兒童數感發展研究[J].中國特殊教育，2018（12）：82-89.

[9]張麗錦，畢遠，梁熠，等.小學一年級數感不良兒童的篩查與動態干預[J].心理學報，2016，48（7）：804-817.

[10]SOWDER J T. Estimation and number sense[J]. Handbook of research on mathematics teaching and learning： A project of the National Council of Teachers of Mathematics， 1992：371-389.

[11] 馬云鵬，史炳星. 認識數感與發展數感[J]. 數學教育學報，2004，11（2）：46-49.

[12] 趙必華，顧海根.心理量表編制中的若干問題及題解[J].心理科學，2010，33（6）：1467-1469.

[13] 鄭日昌.心理測量與測驗[M].北京：中國人民大學出版社，2008：107-120.

[14] KLINE P. A handbook of test construction：introduction to psychometric design [M]. New York： Routledg， 2015： 116-121.

[15] 趙志明.探究小學高段數學如何開展創新教學[J].課程教育研究，2020（12）：136-137.

[16] 王光明，廖晶，黃倩，等.高中生數學學習策略調查問卷的編制[J].數學教育學報，2015，24（5）：25-36.

[17] 王光明，劉丹.初中生數學學習策略調查問卷的設計與編制[J].數學教育學報，2017，26（3）：19-24.

[18] 余曉娟，林子植，徐章韜.結構方程模型在數學教育研究中的應用[J].教育測量與評價，2019（4）：18-24.

[19] 王光明，佘文娟，王兆云.高中生數學元認知水平調查問卷的設計與編制[J].心理與行為研究，2016，14（2）：152-161.

[20] 史靜琤，莫顯昆，孫振球.量表編制中內容效度指數的應用[J].中南大學學報（醫學版），2012，37（2）：49-52.

[21] Hambleton R K ， Swaminathan H ， Algina J ， et al. Criterion-Referenced Testing and Measurement： A Review of Technical Issues and Developments[J]. Review of Educational Research， 1978， 48（1）：1-47.

[22] 侯杰泰，溫忠麟，成子娟.結構方程模型及其應用[M].北京：教育科學出版社，2004：45.

[23] 崔寶蕊，李健，王光明.初中生數學元認知水平調查問卷的設計與編制[J].數學教育學報，2018，27（3）：45-51.

[24] 俞飛丹. 基于腦電的一年級學生數感研究[D].杭州：杭州師范大學，2017.

[25] 滕林林. 基于ERP的低段學生數感發展研究[D].杭州：杭州師范大學，2018.

[26] 王光明，宋金錦，王兆云. 高中生數學學習非智力特征調查問卷的編制[J]. 數學教育學報，2015（3）：17-27.

[27] 郭民. 小學生數感的發展與特征研究[D].長春：東北師范大學，2009.

附錄：問卷三

親愛的小朋友：歡迎參加小測試。請你仔細看題目，按照要求認真回答。選擇題都只有一個正確答案。測試結果只用來做研究，與你的數學成績無關。

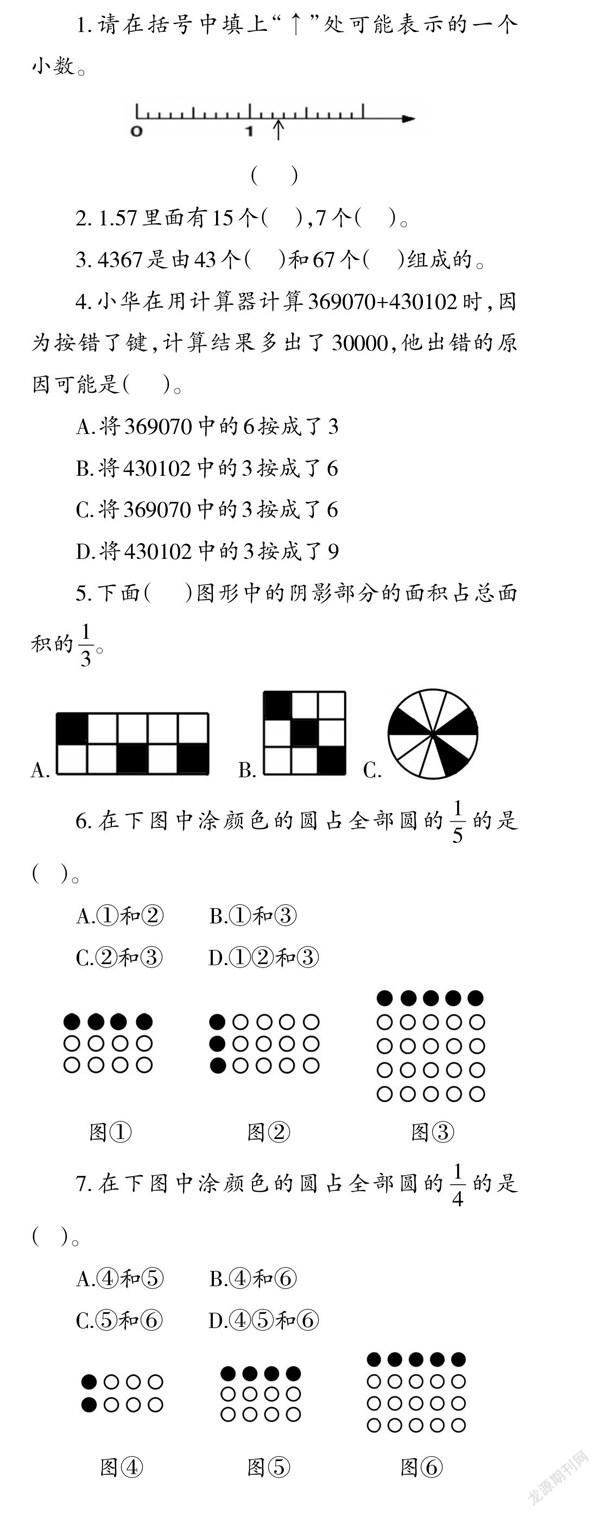
1.請在括號中填上“↑”處可能表示的一個小數。

<Z：＼2021年教師類小學版＼2021年小學數學＼小學數學2021-12＼小學數學2021第12期內芯＼Image＼1_1.jpg>（? ? ?）

2. 1.57里面有15個（? ? ），7個（? ? ）。

3. 4367是由43個（? ? ）和67個（? ? ）組成的。

4.小華在用計算器計算369070+430102時，因為按錯了鍵，計算結果多出了30000，他出錯的原因可能是（? ? ?）。

A.將369070中的6按成了3

B.將430102中的3按成了6

C.將369070中的3按成了6

D.將430102中的3按成了9

5.下面（? ? ?）圖形中的陰影部分的面積占總面積的[13]。

A.<Z：＼2021年教師類小學版＼2021年小學數學＼小學數學2021-12＼小學數學2021第12期內芯＼Image＼2.jpg>? ? B.<Z：＼2021年教師類小學版＼2021年小學數學＼小學數學2021-12＼小學數學2021第12期內芯＼Image＼3.jpg>? C.<Z：＼2021年教師類小學版＼2021年小學數學＼小學數學2021-12＼小學數學2021第12期內芯＼Image＼4.jpg>

6.在下圖中涂顏色的圓占全部圓的[15]的是（? ?）。

A.①和②? ? ? ? B.①和③

C.②和③? ? ? ? D.①②和③

<Z：＼2021年教師類小學版＼2021年小學數學＼小學數學2021-12＼小學數學2021第12期內芯＼Image＼5.jpg><Z：＼2021年教師類小學版＼2021年小學數學＼小學數學2021-12＼小學數學2021第12期內芯＼Image＼6.jpg><Z：＼2021年教師類小學版＼2021年小學數學＼小學數學2021-12＼小學數學2021第12期內芯＼Image＼7.jpg>

圖①? ? ? ? ? ? ? ? ? ? 圖②? ? ? ? ? ? ? ? ? ? ?圖③

7.在下圖中涂顏色的圓占全部圓的[14]的是（? ?）。

A.④和⑤? ? ? ? B.④和⑥

C.⑤和⑥? ? ? ? D.④⑤和⑥

<Z：＼2021年教師類小學版＼2021年小學數學＼小學數學2021-12＼小學數學2021第12期內芯＼Image＼8.jpg><Z：＼2021年教師類小學版＼2021年小學數學＼小學數學2021-12＼小學數學2021第12期內芯＼Image＼9.jpg><Z：＼2021年教師類小學版＼2021年小學數學＼小學數學2021-12＼小學數學2021第12期內芯＼Image＼10.jpg>

圖④? ? ? ? ? ? ? ? ? 圖⑤? ? ? ? ? ? ? ? ? ?圖⑥

8.把[57]，58%，0.57，[35] 四個數，從小到大排列是（? ?）。

A.[35]，0.57，58%，[57]? ? ? ? ? ? ? ? ? ? ? ? ?B.[35]，0.57，[57]， 58%

C.0.57，[35]，[57]，58%? ? ? ? D.0.57，58%，[35]，[57]

9.把[89]，48%，0.49，[25] 四個數，從小到大排列是（? ?）。

A.[89]，0.49，48%，[25]? ? ? ? B.0.49，[25]，48%，[89]

C.[25]，48% ，0.49，[89]? ? ? ?D.[25]，0.49，[89]，48%

10.把[113]，131%，1.3三個數，從小到大排列是（? ? ）。

A.1.3，131%，[113]? ? ? ? ? ? B.131%，1.3，[113]

C.1.3，[113]，131%? ? ? ? ? ? D.131%，[113]，1.3

11.小李和小華帶了一樣多的錢出門，小李花了[13]，小華花了30%。請問，誰剩下的錢多（? ?）。

A.小李? ? ? ? ? ? ? B.小華

C.一樣多? ? ? ? ? ?D.無法比較

12.小明今天走了10179步，他每天堅持走差不多的步數，那么他走1億步大約需要（? ?）。

A.3個月? ? ?B.30個月? ? ?C.3年? ? ?D.30年

13. 如圖⑦，有一個正方形的花園，繞它的周圍走一圈。假設你從O點出發，順著箭頭方向走，大約走了整個路程的[13]后，你的位置大約在哪里（? ?）。<Z：＼2021年教師類小學版＼2021年小學數學＼小學數學2021-12＼小學數學2021第12期內芯＼Image＼11.jpg>

圖⑦? ? ? ? ? A? ? ? ? ? ? ? B? ? ? ? ? ? ? C? ? ? ?; ? ? ?D

14.如果[a]+59=321，那么

（1）[a]+20+（? ? ）=321;（2）[a]-20+（? ? ）=321。

A.39? ? ? ? ?B.59? ? ? ? ?C.79? ? ? ? ?D. 99

理由：

15.如果[b]×10=[c]，那么

（1）[b]×（? ?）=[c]×3;（2）[b]×（? ?）=[c]÷2。

A.5? ? ? ? ? ? ? B.10? ? ? ? ? ? ? C.20? ? ? ? ? ? ? ?D. 30

理由：

16.如果[m]-[n]=60，那么

（1）（[m]+20）-[n]=（? ?）;（2）[m]-（[n]+20）=（? ?）。

A. 20? ? ? ? ? ? ? B. 40? ? ? ? ? ? ?C. 60? ? ? ? ? ? ? D.80

理由：

17.有甲、乙、丙三個數，甲=99×399，乙=398×99，丙=399×101，下列對甲、乙、丙三個數的大小順序的敘述，哪一個是正確的（? ?）。

A.甲=乙=丙? ? ? B.甲>乙>丙

C.乙>甲>丙? ? ? D.丙>甲>乙

理由：

18.[a]，[b]，[c]都是非零自然數，且[b>c]，那么[a-b+c]和[a+b-c]誰更大（? ?）。

A.[a-b+c]? ? ? B.[a+b-c]

C.一樣大? ? ? D.無法比較

理由：

19.[x]，[y]，[z]都是非零自然數，且[y>z]，那么[x÷y×z]和[x×y÷z]誰更大（? ?）。

A.[x×y÷z]? ? ? B.[x÷y×z]

C.一樣大? ? ? D.無法比較

理由：

20.[m]，[n]，[s]，[t]都是非零自然數，且[m÷1.1=n÷0.9=s÷34=t÷65]，那么最小的數是（? ?）。

A.[m]? ? ? ? ? ?B.[n]? ? ? ? ? ? C.[s]? ? ? ? ? ?D.[t]

理由：

（1.浙江省杭州長河中學? ?310053

2.浙江省杭州市余杭區良渚杭行路小學? ?311101

3.杭州師范大學經亨頤教育學院? ?311121）