行星齒輪傳動比速度瞬心計算法研究*

劉 營， 姜雨田， 劉長安

（山推工程機械股份有限公司，山東 濟寧 272073）

0 前言

行星齒輪傳動是一種普遍采用的傳動形式， 它具有體積小、傳動比大、可靠性高等優(yōu)點，在齒輪變速箱中應用廣泛[1-2]。 隨著行星齒輪減速器以及行星齒輪傳動在變速箱中的廣泛應用， 對行星齒輪傳動的計算和分析成為工程機械傳動設計過程中的重要環(huán)節(jié)， 而行星齒輪的傳動比選取計算是行星齒輪的設計過程極為重要的一步[3]。

對行星齒輪的傳動運動分析主要有機構轉化法、速度圖解法等[4]。 機構轉化法是根據(jù)相對運動的原理，在整個行星齒輪系統(tǒng)上附加一個與行星架等大相反的轉速，從而使復雜的兩自由度的齒輪運動問題轉化為齒輪的定軸轉動問題，該方法計算過程簡潔明快，但是比較抽象，越過了行星輪的個體運動，將之簡化為一個惰輪處理，對于了解行星齒輪傳動的運動過程，沒有說明。 速度圖解法較為直觀，各個構件的運動情況都有指示。 但速度圖解法過程相對較為繁瑣[5]。

速度瞬心法是機械行業(yè)用于機構速度分析的一個重要方法， 該方法能夠簡捷直觀地分析機構中某個或某幾個位置的運動特性[6]。 本文嘗試引入平面機構運動分析中常用到的速度瞬心法，以標準漸開線直齒輪為對象，通過分析計算求解行星齒輪的傳動比。

1 方法設計

在如圖1 所示的行星齒輪中，太陽輪、行星輪、齒圈的齒數(shù)分別為Zt、Zx、Zq；太陽輪、行星輪、齒圈、行星架的轉速分別為Nt、Nx、Nq、Nj。 此行星齒輪的特性參數(shù)為α，且圖1 中給出了三者的節(jié)圓（分度圓）以及各齒輪的轉動方向。

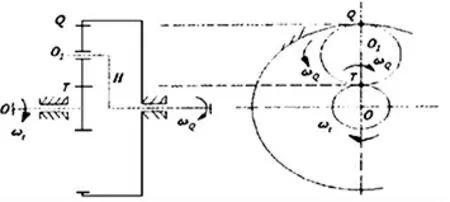
圖1 行星齒輪傳動圖

行星輪在T 點與太陽輪相嚙合，故此處Vxt=Vtt（Vxt、Vtt 分別為行星輪、太陽輪上T 點的速度）；行星輪在Q 點與齒圈相嚙合，故在Q 點處有Vxq=Vqq（Vxq、Vqq 分別為行星輪、齒圈上Q 點的速度）。 行星輪作為平面運動的剛體，在已知其上兩點的絕對速度的情況下，可以求得其速度瞬心，進而計算出其分度圓圓心位置，即行星架與行星輪的接觸點的速度。 下面對行星輪速度瞬心的位置進行求解。

如圖2 所示，設行星輪的速度瞬心為J 點，連接EJ、JA兩條線段。 則相對于速度瞬心J，Q 點的角速度可表示為：

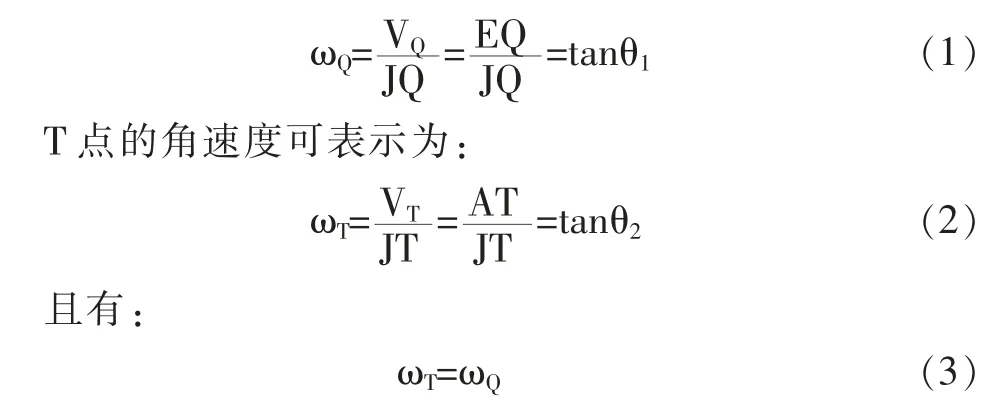
其中：ωT、ωQ分別為行星輪上T、Q 兩點的角速度。

圖2 行星輪速度瞬心位置示意圖

根據(jù)（1）（2）（3）式可得：tanθ1=tanθ2，θ1=θ2，即：E、J、A三點共線。 此時行星齒輪中心位置O1點的瞬時線速度VO1即為行星架上O1點的瞬時線速度，則行星架的旋轉角速度具體的求解過程表述如下：

圖3 行星架旋轉角速度示意圖

如圖3 所示，過O1做線段O1C，用O1C 表示O1的瞬時線速度，即：

參考圖3 幾何關系，由（7）式可知，C 點應在線段AE上。過點Q 做AE 的平行線交TA 延長線于B 點，延長O1C交BQ 于D 點。 四邊形CDQE、ABDC、ABQE 均為平行四邊形，則：

式中：ωT'、ωQ'分別表示太陽輪、齒圈的轉動角速度。 對于行星架上O1點：

式中：ωO1'為行星架上O1點的轉動角速度。 聯(lián)立方程（11）（12）得到：

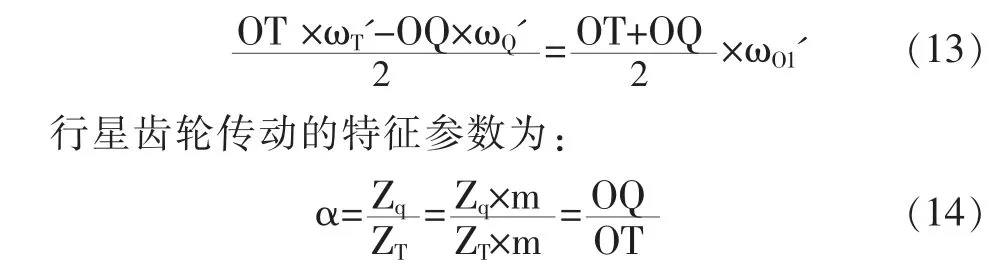
將式（14）代入方程（13）中，整理得到：ωT'-αωQ'-(1+α)ωO1'=0，即：

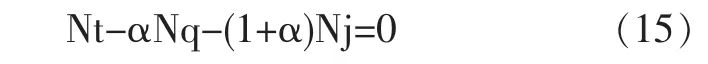
式（15）與采用機構轉化求解法得出的關系式一致。

2 方法分析

因為推理的需要，本文對行星輪的速度瞬心做了必要的證明，過程略顯冗長，在實際應用過程中可以直接應用上述的計算推導結果，包括：

1） 在圖2 中連接TQ 與OO1的交點即為行星輪的速度瞬心。

2） 在圖3 中過點O1做OO1的垂線且與TQ 的交點C，O1C 即為O1點的速度矢量。

行星齒輪傳動的平面自由度為：4×3-2×4-2=2，即行星齒輪傳動需要有兩個確定的速度輸入，才能有唯一的速度輸出，該方法本質上是利用了這一點，計算過程即已知齒圈和太陽輪的速度，求解行星架的速度解析式，通過引入行星輪的速度瞬心，從而建立了三者之間的等式關系。

3 結論

行星齒輪傳動具有傳動比大、傳動平穩(wěn)性好、傳動效率高、結構緊湊等優(yōu)點，被廣泛應用于各種工程機械、運輸車輛等機械設備中。 針對行星齒輪傳動比計算問題，本文在分析已有傳動比計算方法的基礎上，通過借鑒引入平面運動物體的速度瞬心概念，以標準漸開線直齒輪為研究對象，對行星齒輪傳動系統(tǒng)傳動比進行求解，給出了基于速度瞬心的行星齒輪傳動比推導過程，求得了各個構件之間的運動關系，與以往的機構轉化求解法相比， 本方法更能清楚地描述行星齒輪系中行星輪的運動狀態(tài)。