求解0-1背包問題的混合貪婪遺傳算法

陳 楨，鐘一文，林 娟

（1.福建農林大學計算機與信息學院，福州 350002；2.智慧農林福建省高等學校重點實驗室（福建農林大學），福州 350002）

0 引言

背包問題（Knapsack Problem，KP）［1］屬于經典的組合優化問題，屬于NP 難問題［2］，該類問題包括許多變種：0-1KP［3］、有界KP、無界KP、多重約束的KP、多維KP、集合并集的KP、多KP、多重選擇的KP、二次KP、動態KP、折扣KP［4］以及其他類型的KP。在眾多變體KP中，最基本的就是0-1KP。在理論上，許多整數規劃問題的求解都依賴于一個高效的求解KP的算法，因此在實際應用中常常被用于工業、金融等領域，比如投資決策、貨物裝載等。

傳統求解0-1KP 的辦法是精確算法，譬如窮舉法、動態規劃法、遞歸法、回溯法和分支定界法等［4］。精確算法可以得到問題的精確解，但是隨著物品數量和背包容量的增加，算法時間的復雜性呈現出指數級的增長趨勢，計算效率比較低，因此只適合小規模問題的求解。而元啟發式算法作為近似搜索算法，可在較短時間找到問題的近似有效解，逐漸成為解決大規模0-1KP 的主流方法。該類算法大致可分為兩類：以局部搜索為特征的單個體迭代算法，包括經典的模擬退火（Simulate Annealing，SA）算法［5］、混合貪婪修復算子的噪聲檢測算法（Noising Methods with hybrid greedy repair operator，NM）［6］等；以協同搜索為特征的基于種群的智能優化算法，包括常見的蟻群優化（Ant Colony Optimization，ACO）［7］、粒子群優化（Particle Swarm Optimization，PSO）［8］、遺傳算法（Genetic Algorithm，GA）［9］，新興的布谷鳥搜索［10］、帝王蝶優化算法［11］，以及和聲搜索算法（Harmony Search Algorithm，HSA）［12］等，均可見在0-1KP上的應用。

GA作為一種典型的進化型算法，其獨特的選擇、交叉、變異算子以及概率化的尋優方式，使得算法自動獲取解空間的布局，自適應地調整搜索狀態，因此算法具有較好的全局協同搜索能力。但由于GA 缺乏有效的小范圍搜索策略，導致其局部搜索能力較差，在實際應用中，容易產生早熟收斂的問題。為了有效提高GA 在全局大范圍搜索中跳出局部極值解的能力，同時結合0-1KP 的問題特征，本文提出混合貪婪遺傳算法（Hybrid Greedy Genetic Algorithm，HGGA）：在GA 的并行解空間中，增加提高個體的局部求精能力的搜索模塊；并針對常用的基于物品價值密度的修復優化算子僅強調物品的性價比，使得總體價值高但相對性價比低的物品難以被選入，從而導致搜索范圍縮減及收斂速度降緩的問題，提出同時選擇物品價值密度以及物品價值為標準的混合貪婪操作算子，在局部解空間中展開彈性的動態搜索。算法在并行迭代的算法框架中，通過增強GA 的精細搜索能力得到算法求精能力和求泛能力的良好平衡。算法在不同問題性質及大規模的測試集上進行了測試，并通過與同類算法的對比，顯示出較好的性能。

1 相關工作

1.1 0-1背包問題

0-1KP 可以簡單描述為：給定n種物品集合N=｛1，2，…，n｝和一個背包容量為C的背包。每一種物品i都有它的重量wi（＞0）和價值vi（＞0）（i=1，2，…，n）。求最優裝包方案（x1，x2，…，xn），xi∈｛0，1｝（xi=0 表示不把第i個物品放入背包，xi=1 表示把第i個物品放入背包），使得背包的總重量W不超過C的同時獲得的價值V達到最大。在選擇物品裝入背包時，物品只有兩種狀態：整體裝入或不裝入。其數學表達式為：

0-1KP 問題屬于帶有約束條件的最大值優化問題，對違反約束條件的處理通常有兩種方法。第一種是罰函數方法，通過對不可行解增加一個負值罰分從而排查此類解進入下一輪迭代的可能性。另外一種更常見的方法是引入修復優化操作，該操作分為兩個步驟：首先是修復操作，即對不可行解按照一定的準則移除物品，直到該不可行解變為可行解為止；接下來是優化操作，即選擇合適的物品加入，在出現不可行解之前停止。其中，對于物品的選擇標準，通常采用的是基于價值密度的貪婪選擇方法，即優先選擇單位價值（vi/wi）密度大的物品。具體算法描述如算法1和算法2。在兩個算法中，均引入了一個基于價值密度降序排列的物品列表HD，當不可行解出現時，首先采用貪婪修復算子（OPerator-Repair，OP-R）進行修復，根據物品在HD中的排序依次對物品進行考察，如果當前物品在背包中，將其移除，直至背包內物品總量量滿足約束條件為止；隨后采用貪婪優化算子（OPerator-Optimization，OP-O）對該解進行優化，同樣根據HD中物品的順序，優先選擇價值密度大的物品進行加入。

算法1 貪婪修復算子（OP-R）。

1.2 求解0-1背包問題的啟發式算法

GA作為一個經典的啟發式搜索算法，通過對生物遺傳和進化過程中選擇、交叉、變異機制的模仿，來完成對問題最優解的自適應搜索過程，在解決大規模組合問題方面具有較好的表現。其中在解決0-1KP 方面，一般是通過兩種方法進行求解：一種是基于罰函數的基本遺傳算法（Simple GA，SGA）［13］；一種是基于處理約束條件的修復或修復優化的貪婪算子的改進遺傳算法，其中改進遺傳算法較SGA 優越。Michalewicz［14］首先研究了利用GA 求解0-1KP 時個體編碼方法的優劣以及處理0-1KP 不可行解的罰函數法與修復法，指出：GA的個體采用0-1向量編碼比自然數編碼的效果更佳，而且利用修復法處理0-1KP 不可行解比罰函數法的結果更好。從此，人們在利用GA 求解0-1KP 時一般均采用0-1 向量的編碼方式。

GA 的搜索能力由選擇算子、雜交算子決定，變異算子保證算法能搜索到問題空間的盡可能多的點，從而使其具有搜索全局最優的能力，所以一般求解0-1KP的改進GA 也是從這3 個算子上做調整和改進，結合基于修復或修復優化的貪婪算子求得最優解。文獻［15］將貪婪算子與GA 結合起來得到混合遺傳算法（Hybrid Genetic Algorithm，HGA）。在HGA 中首先采用二進制編碼的GA 產生新解，然后通過價值密度引導的貪婪算子對不滿足約束條件的解進行修復。文獻［16］針對HGA 中提出的貪婪算子的缺陷提出新的貪婪算子，不僅僅修復不滿足約束條件的種群，也優化滿足條件的種群，并將此方法與GA 相結合構成一種新的算法GGA。文獻［17］將基于價值密度的貪婪算法與GA 相結合提出一種改進的混合GA來求解0-1 背包問題，改進的混合GA 通過GA 的擇優，重復執行選擇、交叉和變異以及基于價值密度的貪婪算法的修復優化這樣一個過程，使得解無限接近最優解，同時采用精英保留機制來提高算法的收斂速度。文獻［18］用GGA 改進的貪婪算子提出一種改進混合遺傳算法（Improved Hybrid Genetic Algorithm，IHGA），對染色體進行修復和優化，并基于穩態復制的策略，對GA 的選擇操作進行改進，給出了隨機選擇操作。

還有一類改進GA，通過加入模擬退火算法（SA）或改進的SA 來增加局部搜索能力，使得通過GA 的全局搜索方式下求得的解能夠跳出局部極值，并最終趨于全局優化。文獻［19-20］分別運用模擬退火和遺傳算法相結合的方法求解0-1KP，克服了各自的弱點，提高算法的優化性能、優化效率和可靠性。文獻［21］借鑒二重結構編碼的解碼處理方法設計了一種新解碼方法，在保證解可行性的同時修正種群中無對應可行解的個體；采用模擬退火算法和改進的精英選擇算子改進SGA。

上述算法在進化效率或最優解搜索能力上都存在一些不足，因此，受SA具有較強局部搜索能力可以彌補GA的局部求精能力不足的啟發，同時借鑒文獻［6］中貪婪算子的改進方法，本文提出了一種新的混合貪婪遺傳算法，使得局部搜索和全局搜索相互結合，取長補短。

2 改進的混合貪婪遺傳算法

本文提出的改進算法主要針對以下問題：混合GA 的局部求解能力不足、算法傾向早熟收斂；基于價值密度的修復優化方法過分強調價值與重量的比率、無法全面覆蓋優質解且降低搜索速度。本文提出結合局部搜索和混合修復優化算子的混合貪婪遺傳算法，首先在標準的GA 框架下增加局部搜索模塊，并采用基于貪婪思想的混合修復優化算子，對個體展開解空間中的精細更新，有機結合協同搜索和局部搜索的優勢，從而提高算法的整體性能。

2.1 解的表示及初始化

0-1KP 屬于組合優化問題，對于此類問題的解，在GA 中采用二進制編碼方式，即種群中的每一個個體為一個n元0-1向量x，該向量中的每一位隨機取值為0或1，分別表示把此物品放入或不放入背包中。

2.2 全局搜索模塊

本文提出的算法依托標準GA 的全局開拓能力，執行標準GA 的進化框架，在種群隨機初始化產生之后，通過交叉、變異和選擇操作產生新的種群。

1）交叉操作：對初始化種群中的解隨機取兩個染色體作為父母個體，依照交叉概率選擇個體進行均勻交叉操作，生成與父代個體數目一致的子代個體。

2）變異操作：對子個體按照變異概率進行基位變異，對選中的位置上的0/1 編碼進行逆向轉化，即0 變異位1，1 變異為0。

3）選擇操作：采用擇優選擇法，將父代和子代的個體統一按照適應值的降序排序，根據該排序選擇滿足種群數的個體組成新一代的種群。

2.3 局部搜索模塊

通過第一階段的種群進化過程，種群中的個體已覆蓋了較廣的搜索區域，但對于現有范圍的精細搜索，在GA 的算法框架內沒有較好的辦法。因此，在種群總體得到一次進化操作后，對于種群中的每一個個體，增加一個局部搜索模塊，使得每一個個體以自身為搜索起點，在其周圍展開局部范圍內的搜索。具體操作步驟為：對于種群中的每一個個體，隨機對一個位進行翻轉，采用貪婪的方式接受修改，即如果該操作使得對應的適應值得到提高，就接受新解以代替舊解；否則沿用舊解，進行下一輪的局部擾動，直到達到預先設置的局部搜索次數。在后續的操作中，經過新一輪的全局搜索過程，采用GA三個基本操作將優質的局部解信息迅速擴散，同時在局部搜索中出現的極易陷入局部最小值，而貪婪接收方式無法輕易跳出極值的問題，通過全局的進化過程，陷入極值的解得以相應調整并往正確的方向進化。進一步地，在總體迭代條件不變的情況下，通過合理平衡全局迭代次數以及局部搜索次數，在種群中的優良信息得以均勻快速地推廣同時，在較理想的解空間周邊的細致搜索也使得算法找到全局最優解的可能性大大提高。通過這樣全局搜索和局部搜索有機結合的方式，算法在全局求泛和局部求精的性能上得到了良好的平衡。具體算法描述如算法3。在算法3 中，對于種群的每一個個體，隨機選擇一維進行擾動，同時進行修復和優化，如果之后的結果好于原先的解，就替代原先的解，繼續進行下一輪搜索，直到達到局部搜索次數為止。

算法3 局部搜索算法。

2.4 混合貪婪算子

對于在迭代過程中不可行解的處理，通常采用基于價值密度的貪婪修復和優化操作。雖然這種操作方式使得性價比高的物品優先進入背包，但是這種單一的選取方法將導致具有較大價值但相對性價比低的物品無法被選入，而這部分物品的加入可大幅提高算法的全局尋優速度。但是單純選擇價值大的物品同樣也會增加算法陷入局部最優解的概率。因此在HGGA 中采用基于混合策略貪婪修復算子（Operator-Hybrid，OP-H）。該算子借鑒了文獻［6］的混合貪婪修復算子策略，在不可行解時，算法首先采用采用基于價值密度的準則移除性價比最低的物品，在盡量保持現有優質解信息的同時進行有效率的修復；在優化過程中，采用隨機的方式，概率性地選擇基于價值密度或價值的策略，彈性地對解進行優化，在提高算法的收斂速度的同時有效避免陷入極值點。與文獻［6］不同的地方在于：NM算法在不可行解出現時，直接采用概率方法選擇不同的策略同時進行修復和優化，這樣會造成價值大的物品有較大概率被移除出背包，從而降低算法收斂速度。具體算法描述如算法4。

算法4 混合貪婪算子（OP-H）。

輸入 按照價值密度降序排列的物品列表HD，按照價值降序排序的物品列表HV，選擇概率p和不可行解個體x。

輸出 滿足約束條件的優化解x′。

在算法4中，首先基于價值密度的選擇方式調用算法1修復初始解x中的不可行解，接著隨機生成概率r，對于修復過的可行解來說，如果r小于p，采用基于價值密度的選擇方法對個體x進行優化；反之則優選選擇價值大的物品加入x中。

在算法運行過程中，一旦產生新解，上述兩個算子OP-R及OP-O就對該新解分別進行修復和優化的工作。其中，貪心修復算子負責將價值密度最低的物品盡快移除，在對違反約束條件的解進行修復的同時提供進一步優化的空間，貪心優化算子負責對修復后的解進行局部優化。兩個算子協同工作，在解空間中展開合法、有效的搜索。

2.5 HGGA框架

HGGA 主要有3 個重要的組成部分：在初始解隨機生成之后，首先依靠GA 的全局搜索流程，通過經典的交叉、變異、選擇操作進化出新一代種群；然后對種群中的每一個個體展開局部范圍內的更新；對于不可行解的修復過程采用混合貪婪修復算子進行操作。3 個組成部分協同搜索，構造有效解空間，引導整個種群進化，最終找到最優解。具體算法描述如算法5。

算法5 HGGA流程。

輸入 函數評價次數MET，popSize，localTimes，HD，HV。

輸出 最優解Xbest。

3 仿真實驗及結果分析

3.1 測試數據集

為了驗證HGGA 的性能，引入在各文獻中出現的3 個數據測試集分別進行測試。

第1 個測試數據集來自文獻［22］，根據問題特征按照物品質量、價值呈無相關、弱相關和強相關分為3 類，分類特征如表1所示。每類中包含5個測試實例，分別包含物品數量為800、1 000、1 200、1 500 和2 000。在表2 中分別給出這3 類測試例子的具體名稱、物品數目及理論最優解。

第2 個測試數據集的兩個實例（實例1、2）是0-1KP 的經典實例，實例來自文獻［18］，兩個實例的實驗次數均為50 次。n為物品數量，C為背包容量，V為物品價值，W為物品重量。

第3 個測試數據集來自文獻［23］，數據集是大規模的0-1KP 產生的。每個物品的價值是從0.5到1之間隨機生成的，相應的物品重量也是在0.5到2之間隨機生成的。

背包的最大容量被設置為上述物品重量之和的0.75 倍。這些數據都是隨機生成器一次生成的，并且用于所有的實驗。放入背包的物品數量從100 到6 400，包括100、200、300、500、700、1 000、1 200、1 500、1 800、2 000、2 600、3 000、3 500、4 900、5 800、6 400。這些實例被標記為LKP1～LKP16。

表1 第1個大樣本數據的分類特征Tab.1 Classification characteristics of first dataset of large sample data

表2 第1組15個測試例子的參數值Tab.2 Parameter values of 15 test cases in first dataset

3.2 參數設置及運行環境

在HGGA 中，采用函數評價次數MET作為迭代結束條件，取值為40 000；在GA框架下的參數沿用經典的GA參數［24］設置：交叉概率cp取值為0.1，變異概率mp取值為0.01；對于平衡算法全局與局部搜索性能的種群數popSize和局部搜索次數localTimes，在固定的MET條件下，采用實驗的方式決定。混合貪婪算子的選擇概率dp設為0.5。每個測試用例上的實驗獨立運行次數設為100。

實驗的硬件環境為小米筆記本，CPU 型號為Intel Core i5-8250U，內存8 GB，軟件環境為64 位Windows 10 操作系統，算法使用Java語言在Eclipse IDE中編寫。

3.3 參數分析

在相同的函數評價次數下，如何設置種群數和局部搜索次數決定了HGGA 搜索的深度和廣度。如果種群數太大，而局部搜索次數太小，會導致種群在局部范圍內搜索精度不足，從而影響算法整體尋優能力；反之如果局部搜索次數太大，而種群數設置太小，會因算法的多樣性不足而容易出現早熟收斂的現象。選用3.1 節中的第1 組數據集中的重量價值呈強相關的5 個數據集，對于popSize和localTimes分別設置（100，10）、（50，20）、（20、50）、（10、100）進行測試，并觀察100 次重復實驗中Xbest最后一次得到改善時的平均迭代次數。從圖1可以看出，當種群數和搜索次數取（10、100）時，最優解得到最后一次改進所需要的迭代次數最少，所以這種搭配可以對算法在多樣性和收斂性上達到一個比較均衡的平衡。因此，算法最終的popSize設置為10，localTimes設置為100。

圖1 不同參數組合下算法最后一次得到改進所需的平均迭代次數對比Fig.1 Comparison of mean iterations required by the algorithm to have the last improvement under different parameter combinations

對于混合貪婪算子中使用的選擇概率dp的取值，采用實驗統計方式進行。當dp取0 和1 時，分別代表只采用基于價值和密度和只采用價值作為選擇準則的操作算子。測試選用3.1 節的表2 的3 組大樣本數據的15 個測試數據集，dp分別取0、0.1、0.2 取到1，統計15 個測試用例在不同取值下得到最優解的個數。結果如圖2所示。

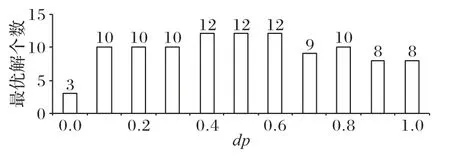
圖2 不同dp取值在15個測試例子上取到最優解的個數對比Fig.2 Comparison of the number of obtained optimal solutions on 15 test cases with different dp values

當dp=0 時，僅有3 個測試用例能夠得到最優解，當dp在0.4～0.6 時，能夠取到的最優解的個數最多。因此，為了增強算法的普適性，在本文中dp取值為0.5。

3.4 算法性能分析

為了測試HGGA 性能，在第1 個數據集上進行了測試。算法獨立運行100 次，統計得到的最優解與理論最優解的實際差值、最優解、最差解、均值解、中位數解和標準差，適應值最后一次得到提高時的迭代次數，運行時間以及在100 次重復中得到最優解的成功率。表3 給出測試結果。粗體部分為獲得最好狀態的解。

從表3 中可以看出，本文提出的算法在所有15 個測試用例上均能找到最好解，對于其中的11 個測試用例可以百分百找到最優解。雖然在KP01、KP08、KP09 上的成功率較低，但是通過觀察其找到的均值解、中位數解以及最差解可以看出，HGGA 所能找到的解與最優解非常相近，并且所有測試均在1 s內完成100次重復性實驗，顯示了算法的良好性能。

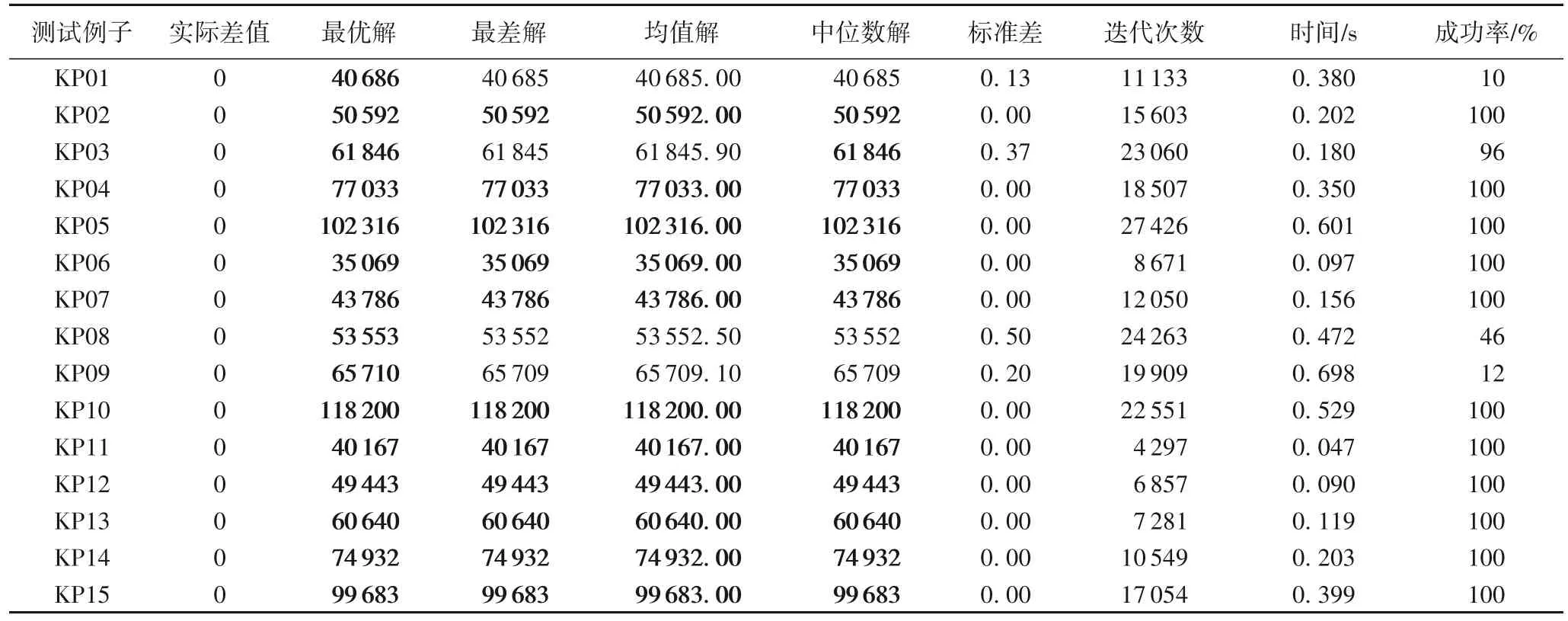
表3 HGGA在15個不同類型測試例子上的結果Tab.3 Results of HGGA on 15 test cases with different types

3.5 與同類算法的比較

為了進一步顯示HGGA 的算法性能，引入不同的測試數據分別與其他GA 以及近年來表現較好的其他新型算法分別進行縱向及橫向的比較。

3.5.1 與GA的比較

測試數據采用上述第2 個測試數據集，背包里的物品數目分別取50和100，所有結果的數據均來源于原文獻。其中，HGA 是使用貪心變換與GA 結合的貪心GA［15］，IHGA［18］是改進的混合GA。n代表物品個數，算法獨立運行50 次，J為50次實驗中得到的最好解，JC代表最好解在50 次內出現的次數，JZ代表繁殖代數的均值。cp和mp分別采用與文獻中相同的設置值0.5和0.01。表4給出與其他GA的比較結果。

從表4 可以看出，HGA、IHGA 和HGGA 在背包里的物品數目取50時都得到最優的結果，HGGA 在50次實驗中每次都能求出最優值，而背包里的物品數目取100 時，只有HGGA 能得到最優解，而且50 次實驗中都能找到最優解。從這兩個結果可得出，HGGA 與同類算法相比，在小規模的測試數據上具有較好的性能。

表4 不同改進遺傳算法求解0-1KP的結果Tab.4 Results of different improved genetic algorithms in solving 0-1KP

3.5.2 與其他元啟發算法的比較

為了進一步測試算法性能，算法與其他同類型的元啟發算法在不同規模的問題上進行了比較。進行比較的算法為：基于全局和諧搜索的混合布谷鳥搜索算法（hybrid Cuckoo Search algorithm with Global Harmony Search，CSGHS）［10］、二元帝王蝶優化（Binary Monarch Butterfly Optimization，BMBO）算法［11］、混沌帝王蝶優化（Chaotic Monarch Butterfly Optimization，CMBO）算法［22］、基于對立學習的帝王蝶優化（Opposition-based learning Monarch Butterfly Optimization，

OMBO）算法［25］和混合貪婪修復算子的噪聲檢測算法（NM）［6］。表5～7分別給出了3組數據上的表現。

表5 HGGA與其他元啟發算法在求解5個無相關特征0-1KP時的數據對比Tab.5 Data comparison of HGGA and other meta-heuristic algorithms in solving 5 0-1KPs without correlation characteristics

表5 的數據表明，在大樣本的物品價值和數量無相關的測試數據中，CMBO、OMBO、NM 和HGGA 比CSGHS 和BMBO在找到最優解上表現得更好，NM 在KP01 的測試數據里表現略差，CMBO 和OMBO 在KP03 上表現較弱。HGGA 在這5 個例子中最差解、均值解和中位數解上的表現都比CMBO、OMBO 和NM 好。在方差std的測算上，HGGA 的總體表現也是最好的，足見該算法的穩定性。表6 顯示了這些算法在求解5 個無相關特征的0-1KP 數據上的平均排名，對于KP05，CSGHS 和BMBO 沒有數據，取KP01～KP04 排名的平均值作為KP05 的排名取值，并對這些排名數據進行0.05 顯著性水平條件下的Friedman 檢驗，得到的p值等于0.003，說明這些算法在排序值上有顯著性差異。

表6 6個算法在求解5個無相關特征的0-1KP時的平均排名Tab.6 Average ranking of 6 algorithms in solving 5 0-1KPs without correlation characteristics

表7 的數據表明，在大樣本的物品價值和數量呈弱相關的測試數據中，CMBO、OMBO、NM 和HGGA 比CSGHS 和BMBO 表現得好。OMBO、HGGA 在5 個測試算例中都得取得最優解，CMBO 在KP08，NM 在KP09 上沒有取得最優解。HGGA 在最差解、均值解和中位數解上綜合表現是勝出的，方差也較小。表8 顯示了這些算法在求解大樣本的物品價值和數量呈弱相關的測試數據上的平均排名。對于KP10，CSGHS 和BMBO 沒有數據，取KP06～KP09 排名的平均值作為KP10 的排名取值，在0.05 顯著性水平條件下的Friedman 檢驗得到的p值為0.004，說明這些算法在排序值上有顯著性差異。

表7 HGGA與其他元啟發算法在求解大樣本弱相關特征的0-1KP時的數據對比Tab.7 Data comparison of HGGA and other meta-heuristic algorithms in solving 0-1KPs with weak correlation characteristics of large samples

表8 6個算法在求解5個大樣本弱相關特征的0-1KP的數據的平均排名Tab.8 Average ranking of 6 algorithms in solving 5 0-1KPs with weak correlation characteristics of large samples

表9 的數據表明，在大樣本的物品價值和數量呈強相關的測試數據中，CMBO、OMBO、NM 和HGGA 比CSGHS 和BMBO 表現得好。CMBO、OMBO、NM 和HGGA 在5 個測試算例中都取得最優解。NM 和HGGA 的方差在5 個例子里都為0，說明算法的在這個測試數據集上的表現非常穩定。表10顯示了這些算法在求解大樣本的物品價值和數量呈強相關的測試數據上的平均排名。對于KP15，取KP11～KP14 排名的平均值作為KP15 的排名取值，在0.05 顯著性水平條件下通過Friedman 檢驗得到的p值為0.002，說明這些算法在排序值上有顯著性差異。

表9 HGGA與其他元啟發算法在求解大樣本強相關特征的0-1KP時的數據對比Tab.9 Data comparison of HGGA and other meta-heuristic algorithms in solving 0-1KPs with strong correlation characteristics of large samples

表10 6種算法在求解5個大樣本強相關特征的0-1KP的數據的平均排名Tab.10 Average ranking of 6 algorithms in solving 5 0-1KPs with strong correlation characteristics of large samples

值得說明的是，HGGA 與除NM 之外的其他比較函數一樣，屬于基于種群的優化算法，因此針對0-1KP，它們的算法時間復雜度均取決于外層迭代數目、種群數目及物品數量；而NM雖然不屬于基于種群的算法，但其迭代過程類似地取決于外層迭代數目、內層局部搜索迭代數目及物品數量；進一步地，雖然HGGA加入了局部搜索部分，但這個部分的時間復雜度取決于局部搜索迭代次數、種群數目及物品數量，并不影響整體算法復雜度，因此這幾個參與比較的算法均具有相同的時間復雜度，而HGGA 可以在更少的函數評價次數內找到優質解。

3.5.3 在大規模數據集上的比較

為了進一步測試算法在大規模數據集上性能，采用上述第三組測試用例，進行比較的算法為：大型0-1 背包問題的簡化二進制和聲搜索（Simplified Binary Harmony Search，SBHS）算法［23］，表11 給出了不同的算法在16 個測試數據上的表現。表11 的數據表明，在這16 個大型0-1KP 的測試數據中，對于前6 個數據，SBHS 和HGGA 的最優解相同，而HGGA 在最差值、均值解和中位數上的表現都均優于SBHS。在數據LKP7-LKP14 中，HGGA 在各指標上的表現都優于SBHS；在數據LKP15中，SBHS的均值解和中位數解較優；在數據LKP16中，SBHS解的所有表現都會比HGGA略好。

在標準差上，除了最后一個測試例子外，HGGA 在每一個測試用例上的表現均優于SBHS，足見HGGA 在大規模的測試數據上的穩定性。

表11 HGGA與SBHS算法在求解大樣本強相關特征的0-1KP時的數據對比Tab.11 Data comparison of HGGA and SBHS algorithms in solving 0-1KPs with strong correlation characteristics of large samples

4 結語

針對GA 在解決大規模離散優化問題上全局搜索能力強、局部求精能力薄弱的缺點，本文提出混合了局部搜索算子的改進GA。算法在不變動GA 的基本框架下，融合具備局部精細搜索能力的局部搜索方法，使得算法得以依賴GA 的強大全局搜索性能將局部搜索中得到的優質解快速擴散；同時設計混合貪婪修復算子，在個體保留優良信息的同時提高算法的尋優速度。算法應用于0-1KP，在不同問題規模及性質的測試集上進行大量的仿真實驗，通過與其他同類算法的比較顯示出算法的高效性和穩定性，特別是在大規模數據集上的有效性。

今后的工作將進一步挖掘局部搜索和基于種群的新型智能優化算法的有機融合，并擴展到更大的應用范圍，例如多維KP、折扣KP等。