基于彈簧投影模型的布料快速仿真

萬 燕, 朱甜甜, 姚 礪, 馮子涵

(東華大學 計算機科學與技術學院，上海 201620)

隨著數字化影業的蓬勃發展，3D游戲、虛擬試衣和動畫電影迅速發展，成為了熱門的新興產業。動畫中虛擬角色建模是一個重要的環節，其中，服飾層的建模工作量占80%以上，要使虛擬角色具有令人滿意的真實感，布料動畫是必不可少的。因此，有關布料模擬一直是研究熱點。

布料動畫[1]主要是在計算機中建立布料的虛擬模型，產生逼真的形變，實現高度真實感和實時的動態效果。早期的布料建模主要采用幾何方法，但該方法通常只產生布料的靜態變形狀態，很難實現真實連貫的復雜動畫。隨著計算機圖形學技術的發展，采用物理方法[2]來模擬布料受到越來越多專家和學者的青睞。物理方法將布料視為連續的彈性介質(如有限元模型[3])，或者由相互作用的非連續粒子組成(如質點-彈簧模型[4])。盡管不同的物理建模方法對于布料的表達方式不盡相同，但是大部分是根據牛頓運動定律計算布料的基本形態。基本形態在數學上的表現形式為動力學方程，針對不同的動力學方程進行求解，需要對模型進行改進。

其中，質點-彈簧模型為表現柔性材料動態特性的建模提供了一種簡單而實用的方法，這些柔性材料包括布料[5]、頭發[6]和可變形固體[7]。然而，與其他用于彈性物體的建模方法一樣，獲得真實的柔性材料行為通常需要本構參數，這些參數與剛性系統的數值計算方法有關。數值計算方法主要有顯式時間積分和隱式時間積分。顯式時間積分方法具有快速性，但是當應用于剛性系統時，其會出現不穩定的問題。Baraff等[8]使用隱式時間積分方法進行數值計算，該方法能夠保證穩定性，但是需要求解大的非線性方程組。由于大的非線性方程組的計算量大，這限制了隱式時間積分方法在實時應用中的使用。另外，就模擬精度而言，隱式積分引入過多的近似，由此造成的過度數值阻尼問題會嚴重影響模擬質量。

牛頓法以其出色的收斂特性而聞名。當迭代足夠接近最優解時，牛頓方法表現出二次收斂性，這優于塊坐標下降法的線性收斂性。但是，牛頓法的每次迭代都需要重新求解系統海森矩陣的逆矩陣，這增加了系統的計算成本。因此，在系統有限的計算成本下，根據獲得穩定、可視化的布料效果實際需求，只使用牛頓法一次迭代下的解，這是未完全收斂下的數值解，距離實際的精確解還存在較大誤差。

Müller等[9]提出的位置動力學(position based dynamics， PBD)法從約束投影的角度來模擬各種物體的材料屬性。由于其健壯性、簡單性和快速性，PBD在游戲和動畫行業中得到廣泛應用。PBD與傳統的彈性模型和本文的彈簧投影不同，其使用了與標準胡克模型不兼容的參數，因此，模擬材料的剛度會受到迭代次數的影響。

針對以上問題，本文提出了一種應用于質點-彈簧系統的隱式快速解算器，該解算器重新優化了Martin等[10]提出的隱式歐拉時間積分能量最小值表達式。相對于使用傳統的牛頓法，本文通過引入輔助變量(彈簧方向變量)，重新推導隱式歐拉時間積分能量最小值表達式，將原有的非線性方程組轉化為若干個小的獨立的非線性方程，之后使用塊坐標下降法求解最佳彈簧方向，即系統能量最小化時彈簧的方向向量，進而根據最佳彈簧方向向量求得整個系統的解。由于分解后的系統矩陣是相互獨立的，因此，可以使用預先計算的稀疏Cholesky因子分解矩陣，從而加快解算速度。

1 質點-彈簧模型系統

構建能夠表達布料變形特性的力學模型是服飾動畫首先要考慮的基礎問題。質點-彈簧模型是一種形式簡單、適合表現柔性材料動態的模型，目前在布料動畫中得到廣泛應用。

首先，假定布料是3D中m個離散質點組成的系統，其還包括一個離散的時間集合，形如t1，t2, …，tn，時間步長為h(通常設h=1/30 s)，假定Ρn∈3m作為在時間tn下質點系統的位置，同時系統遵守牛頓動量守恒定律，作用于質點上的力由非線性函數表示為f:3m→3m，f(Ρn)是作用在質點上的力向量。質點的位置只與這個力向量有關。假定力是守恒力，而守恒力在物理上是指該力對物體所作的功，僅與物體的位置變化量有關，而與路徑無關。常見的守恒力有彈簧力和重力。這里該力表示為f=-E，其中E：3m→為勢能函數(非線性且不收斂)。質點-彈簧模型的最終目標是計算出彈簧系統質點的各個狀態Ρ1，Ρ2，…，Ρn。

給定質量矩陣M∈3m×3m, 根據隱式歐拉積分：

Ρn+1=Ρn+hvn+1

(1)

vn+1=vn+hM-1f(Ρn+1)

(2)

式中：vn和vn+1分別為tn和tn+1時刻的質點速度，f(Ρn+1)表示作用在質點Ρn+1上的力向量。根據式(1)和(2)，質點速度的表達式為

hvn=Pn-Pn-1

(3)

hvn+1=Pn+1-Pn

(4)

聯合式(3)和(4)以消除式(2)中的速度因子，推導出式(5)。

Ρn+1-2Ρn+Ρn-1=h2M-1f(Ρn+1)

(5)

式(5)是牛頓第二定律的離散表達版本(通常其表示為F=ma)，如果Ρn和Ρn-1的狀態已知，那么，由式(5)可以求出Ρn+1的狀態。

關于非線性系統式(5)的經典解法是Baraff等[8]提出的在已知狀態下力的系統線性化，如式(6)所示。

f(Pn+1)≈f(Pn)+(f|Pn)(Pn+1-Pn)

(6)

M(x-y)=h2f(x)

(7)

由式(7)推導出新的變形隱式積分函數，如式(8)所示。

(8)

2 彈簧投影過程

在質點-彈簧模型中，傳統胡克定律下的彈性函數是非線性非凸的，求解整個大的系統耗時長、成本高。但是，將大的系統分解為許多小的可以解決的凸問題，不僅易于求解，而且易于并行化，可加快求解速度，這也是本文基于彈簧投影算法的主要思想。因此，這里重新定義能夠使用塊坐標下降法的勢能函數E的方程，將整個仿真問題轉換為求解隱式歐拉能量方程最小值問題。其中，引入輔助變量將整個大的非凸非線性系統分解為若干個小而獨立的凸問題，接著用塊坐標下降法求解新的能量方程。

在質點-彈簧系統中，勢能函數的主要組成部分是慣性勢能和彈性勢能。慣性勢能是線性方程，比較容易求解，因此本文主要是對彈性勢能方程進行改變。

根據胡克定律，彈簧彈性勢能定義為

(9)

式中：p1,p2為彈簧兩個端點，p1，p2∈3；r為彈簧原始長度，r≥0；k為彈簧的硬度參數，k≥0。

即使是如此簡單的彈性系統，卻是一個非凸函數，非線性和非凸函數特性使得基于牛頓法的解算代價比較高。非線性使得系統每次都要重新計算海森矩陣，而非凸使得海森矩陣是非正定的，這將導致計算無法進行。從運行效率的需求上來看，理想的系統是一個凸函數且有恒定矩陣，或者可以分解成許多小而獨立的非凸問題，能夠并行運行。為此引入帶約束的輔助變量d表示彈簧原長。重新定義勢能函數的關鍵在于，式(9)表示的彈性勢能函數是帶約束的能量最優化值問題。

對于每個彈簧的端點p1，p2∈3并且r≥0：

(10)

式(10)的證明如下所述。

證明定義p12∶=p1-p2，考慮到‖d‖=r，重寫式(10)的左邊變量為

(‖p12‖-r)2=(‖p12‖-‖d‖)2

根據逆三角不等式，得出：

(‖p12‖-‖d‖)2≤(‖p12‖-d)2

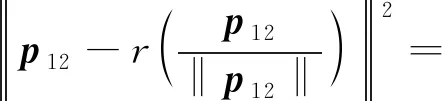
至此證明了式(10)。

(11)

將所有的彈簧勢能加在一起，獲得整個質點彈簧系統的彈性勢能，如式(12)所示。

(12)

經過整理得到式(13)。

(13)

將式(13)轉換成線性矩陣之后，得到式(14)。

(14)

式中：s為彈簧總數；i1,i2∈{1, 2, 3, …,m}為第i個彈簧端點的編號；向量X=(p1, …,pm)；矩陣L∈3m×3m，J∈3m×3s的定義如式(15)所示。

(15)

式中：Ai∈m為彈簧i的關聯向量，即該彈簧質點與其他質點是否組成彈簧，如果組成彈簧，則值為1，否則為-1，例如，Ai,i1=1,Ai,i2=-1；Si∈s為彈簧i的方向，即彈簧i在原長狀態下的旋轉量；I3∈3×3為單位矩陣；?為克羅內克積。事實上，矩陣L是質點-彈簧系統圖的剛度權重圖。

接下來，加入外力(重力、交互力、碰撞響應力)fext∈3m，那么系統的勢能函數為

(16)

式中：U={(d1,…,d2)∈2s:||di||=ri}為彈簧原長狀態的方向向量，將式(16)代入式(8)，則得式(17)。

(17)

式(17)中的最小值就是隱式歐拉時間步長的精確解。

3 阻尼力和碰撞響應

碰撞檢測和響應處理是布料模擬的關鍵和難點問題，其解決方法的優劣直接影響布料仿真的實時性和精確性。

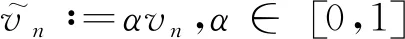
碰撞力也是外力的一部分，可以將其直接加入fext項，進而在全局步驟中參與計算。

在加入阻尼力和碰撞力之后，隱式歐拉方程為

(18)

本文使用塊坐標下降法[12]求解式(18)的最小值優化問題。

本文解算器算法如下：

(1) 初始化X∶=y

(2) 循環：

1) 局部步驟：給定X，找到對于所有彈簧最優的方向得到d。

2) 全局步驟：固定d，求解X：(M+h2L)X=My+h2Jd+h2fext。

(3) 直到收斂或者超出時間限制。

從對X的初始猜測(這里使用y)開始，首先調整X并計算d(局部步長)的最佳方向值，其次，調整d并計算X的最佳值(全局步長)，重復此過程，直到達到最大迭代次數為止。與以前方法不同，本文在求解d的局部步驟中不需要奇異值分解，而僅需要向量歸一化。在求解X的全局步驟(固定d)中，需要解決凸二次最小化問題。實際上，因為L是對稱的且為正半定的，所以系統矩陣M+h2L是對稱正定。而且隨著迭代開始，粒子質量、彈簧剛度和連通性保持不變，系統矩陣將保持不變。因此，本文預先計算了系統稀疏矩陣的Cholesky因式分子，這將使得線性系統求解速度非常快。

加入輔助彈簧后彈簧狀態在整個系統中經歷3個狀態之間的轉換如圖1所示。圖1(b)局部狀態對應解算器的局部步驟，可抽象為彈簧處于原長狀態，稱為最佳彈簧方向，此時系統彈性勢能最小，系統處于穩定狀態；圖1(c)全局狀態對應解算器的全局步驟，根據局部狀態下的彈簧方向向量，可以求出質點的位置向量，也就是系統的全局解。

4 試驗與結果分析

在布料實時模擬中，通常使用一個常量時間步長h確定目標幀速率。Baraff等[8]使用了半隱式積分法，該方法在h=1/120、1/60 s時比較正常，而h=1/30 s時系統矩陣的解將可能不收斂。為了避免這個問題，Baraff推薦使用自適應時間步長，但這將導致系統運行時間大大增加，系統代價過大。

一般而言，在實時系統中，h=1/30 s時仿真效果比較能讓人接受，因此本文采用時間步長h=1/30 s。

本文方法與牛頓法針對一塊2 500個質點的布料進行模擬數值解的比較，結果如圖3所示，其中，相對誤差定義如式(19)。

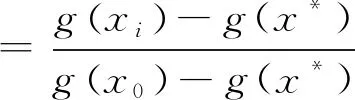
(19)

式中：x0為初始狀態值；xi為當前狀態值；x*為精確解的值。

由圖2(a)可知，本文方法整體呈現線性收斂，牛頓法呈現二次收斂[13]。但是，在有限的計算成本下，牛頓法只迭代1次，在這種情況下，本文方法只迭代一次的相對誤差小于牛頓法(圖2(a)中的A點)。也就是說，在迭代的初始階段，本文方法的表現優于牛頓法。由圖2(b)可知，本文方法在迭代100次以內數值解的相對誤差低于牛頓法的相對誤差(如圖2(b)中的C點)。表1列出了本文算法在A點、B點、C點的時間效率和相對誤差，其分別代表布料動畫在迭代1、10、100次時的運算結果。牛頓算法的1次迭代相對誤差和迭代時間分別為0.250和181 ms。由表1可知，本文算法的相對誤差更小，并且運行時間更短。

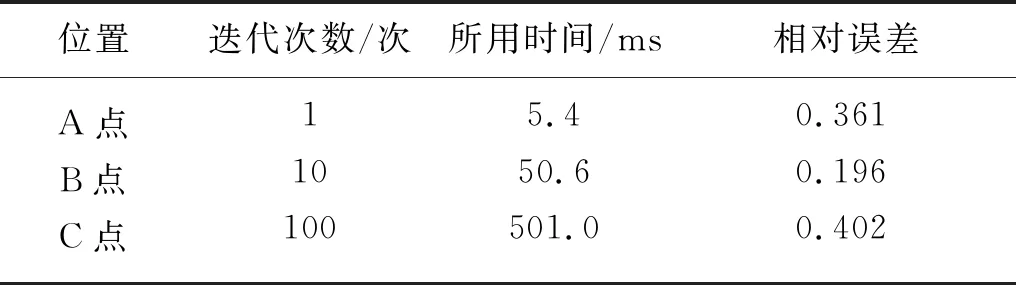
表1 本文算法的時間效率及相對誤差

雖然本文方法的整體收斂速度無法趕上牛頓法的整體二次收斂，但是，本文方法在在第一階段(阻尼階段)優于牛頓法。當迭代的xi值接近于x*時，將本方法的結果作為牛頓法的一個起點，可以加快計算速度。

當時間步長=1/30 s時，使用本文方法和牛頓法模擬同一布料的動畫效果和幀速率表現，如圖3所示。由圖3可知：本文方法的一次迭代已經產生穩定合理的模擬(見圖3(a))，但是褶皺細節相對不明顯；10次迭代在速度與質量上得到比較好的平衡，如圖3(b)所示。

在幀速率表現方面，由圖3可知，本文方法迭代1次和10次的模擬幀速率約為30幀/s，滿足實時動畫要求，而牛頓法的1次迭代的幀速率只有7.6幀/s，無法應用在實時應用中，只能離線渲染。一般而言，幀速率越大，動畫畫面看起來越流暢。由上述分析可知，本文方法在長時間步的布料模擬系統中表現良好。

當模擬的布料有2 500個質點，共有4 802個三角形，時間步長=1/30 s，在不同迭代次數下，PBD法的布料模擬效果如圖4所示。由圖4可以觀察到，在相同的時間步長下，基于PBD的布料模擬迭代次數為1時，布料出現過拉伸現象，隨著迭代次數成倍增加，布料變得更加“僵硬”。這是由于PBD在增加迭代次數時會增加系統的有效剛度，導致剛度參數與標準胡克模型不兼容。但是本文方法不存在這個問題，即隨著迭代次數成倍增加并沒有增加系統的有效剛度，實際表現為布料模擬效果不會過度受迭代次數的影響。

在碰撞處理方面，本文設計了一個窗簾模型布料與小球交互的試驗，以測試本文的方法在接觸和碰撞情況下的行為，實際結果如圖5所示。

由圖5可以看到布料自碰撞和小球交互碰撞的效果，布料的垂墜感和褶皺基本符合現實中布料的物理特性。由此證實本文方法的有效性和實用性。

5 結 語

本文基于質點-彈簧投影模型的布料仿真算法提出了一種改進的模型求解非線性數值方法，用于隱式歐拉時間步長的質點-彈簧系統。該算法在布料模擬的動力學方程中引入輔助彈簧方向變量，將原有的非線性方程組轉化為若干個小的非凸方程，然后，利用塊坐標下降法來求解每一個非凸方程，從而實現快速的迭代。雖然本文方法的整體收斂性不如牛頓法，但是，在牛頓法只迭代一次的情況下，本文方法的數值解相對于精確值的誤差比牛頓法要小，相對誤差曲線斜率更大，即在布料模擬初始階段，本文方法的求解速度更快，并且數值解更接近精確值。本文的方法非常適用于對實時性要求高的系統，也可以將本文的方法應用于系統的初始仿真階段，后續可以繼續采用牛頓法用于仿真，有利于提高系統的整體仿真速度。同時，該方法也克服了PBD方法的布料模擬剛度受約束投影迭代次數影響的缺點，具備良好的實時性和穩定性。