開口圓柱殼的振動響應分析

張峪維，束永平

(東華大學 機械工程學院， 上海 201620)

板殼式薄壁構件是許多工程結構如壓力容器、管道、潛艇船體、飛機的機翼和機身、火箭、導彈以及機器的外殼等最常用的結構元素。殼體的受力主要取決于它的曲率，在保持殼體的厚度和材料不變的條件下改變殼體的曲率，可獲得不同的殼體承載能力。因此，曲率、厚度和邊界條件等參數(shù)是影響甚至決定殼體性能的重要因素。殼體結構的行為特殊性、分析難度以及應用廣泛性，引起學者對殼體分析的廣泛興趣。Love[1]通過總結并拓展Rayleigh的工作，構建了Love殼體振動的基本理論。Warburton[2-3]研究了圓柱殼的受迫振動問題，為受徑向周期力的殼體求得了強迫振動的模態(tài)廣義坐標。Leissa等[4]基于Novozhilov理論，討論了圓柱殼受到正弦波激勵的穩(wěn)態(tài)響應問題。但是由于模態(tài)耦合的問題，共振響應的峰值和阻尼并不是完全成反比，而是存在微小偏差。Kraus等[5]對均勻薄圓柱殼在諧波徑向力作用下的響應進行研究。Liao等[6]得出了圓柱殼對諧波徑向力響應的數(shù)值結果，預測了圓柱殼在共振時的無限響應。Lu[7]研究了無限長圓柱殼在徑向力和黏滯阻尼理論下的響應。

在各種殼體結構中，封閉圓柱薄殼結構被研究得最多。由于圓柱殼的運動方程以及邊界條件比梁和薄板復雜得多，因此要得到圓柱殼的解析解是非常困難的，其主要難點在于如何簡化和求解這些方程[8]。對于開口圓柱殼的研究主要集中在自由振動(模態(tài)和振型)[9]方面，目前文獻中尚未見到關于具有阻尼的開口圓柱殼的振動響應分析。

本文利用解析法分析了四邊簡支開口圓柱殼在簡諧激振力作用下的穩(wěn)態(tài)響應，給出殼體在3種不同阻尼下不同位置的徑向振幅隨激勵頻率的變化情況。對其與7種開口圓柱殼在前10階模態(tài)頻率處的共振響應以及隨模態(tài)數(shù)增加的收斂性進行分析，探究了長徑比、厚徑比、開口角度對穩(wěn)態(tài)響應的影響。本文提供的開口圓柱殼的振動響應和精度可用于近似求解結構振動響應和精度。

1 開口圓柱殼的計算模型

開口圓柱殼的示意圖如圖1所示。采用薄殼基本假設[10]：(1)變形前垂直于中面的直線在變形后仍保持直線，并垂直于中面；(2)相對于其他應力分量，沿中面垂直方向的法向應力可忽略不計；(3)忽略殼體的轉動慣量；(4)法向撓度沿中面法線上各點是不變的；(5)殼體是等厚度的薄殼，其厚度小于殼體長度和曲率半徑的10%。

設殼的厚度為h，中面半徑為R，長度為L，開口角度為θ0，在柱坐標系中坐標原點O位于圓柱殼的前端面圓心處，x軸與圓柱殼的軸線重合，z軸沿圓柱殼的徑向，切向θ為周向偏轉角，u、v和w分別為中面上任意一點P沿軸向、切向和徑向的位移。

2 固有頻率求解

開口圓柱殼的動力學方程[10]為

(1)

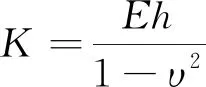
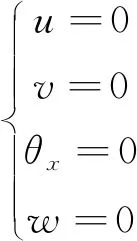
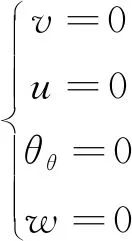
(2)

設四邊簡支開口圓柱殼的振型解[10]為

(3)

式中：下標m和n表示相應振型沿軸向有m個半波、沿周向有n個半波，對應一組(m,n)有3個頻率(i=1, 2, 3)，代表U、V和W彼此的比值不同，但均有m個軸向半波和n個周向半波。3個頻率中最低頻率對應徑向位移較大而軸向位移和周向位移都較小的振動(i=1)，其他兩個頻率值要比其高一個數(shù)量級；中間頻率對應軸向位移分量最大而其他兩個位移較小的運動(i=2)；最高頻率對應周向位移最大而其他位移較小的運動(i=3)。ωimn為固有圓頻率[10]。

將此解代入動力學方程得：

(4)

令系數(shù)行列式等于零可求解出固有頻率系數(shù)，再代入式(4)可求得方程組的通解為

C1mn、A2mn、B3mn未知。

3 響應求解

設在殼體中面上一點(ξ,η)處有簡諧力作用，其外載荷：qx=0為軸向外載荷，qθ=0為周向外載荷，qz=Poiδ(x-ξ)δ(y-η)ejωt為徑向外載荷，其中Poi為徑向外載荷幅值。令Poi=1，則式(1)的位移響應解為

(5)

式中：ω為外載荷圓頻率；M、N為位移響應疊加量，均為無窮大正整數(shù)。

將式(5)代入式(1)，整理得：

(6)

(7)

整理式(7)可得：

(8)

將式(8)兩邊分別乘以相應陣型(9)，并對開口圓柱殼的中面進行面積分，整理得式(10)。

(9)

(10)

求解方程組(10)即可得出響應值系數(shù)Aimn、Bimn和Cimn。

4 計算實例與分析

7種開口圓柱殼的材料參數(shù)均為E=2.1×1011Pa，泊松比υ=0.3，密度ρ=7 850 kg/m2；復阻尼系數(shù)γ分別取0.01、 0.05和0.20。開口圓柱殼的材料參數(shù)與尺寸參數(shù)如表1所示，其中，L/R為長徑比，h/R為厚徑比，θ為開口角度。

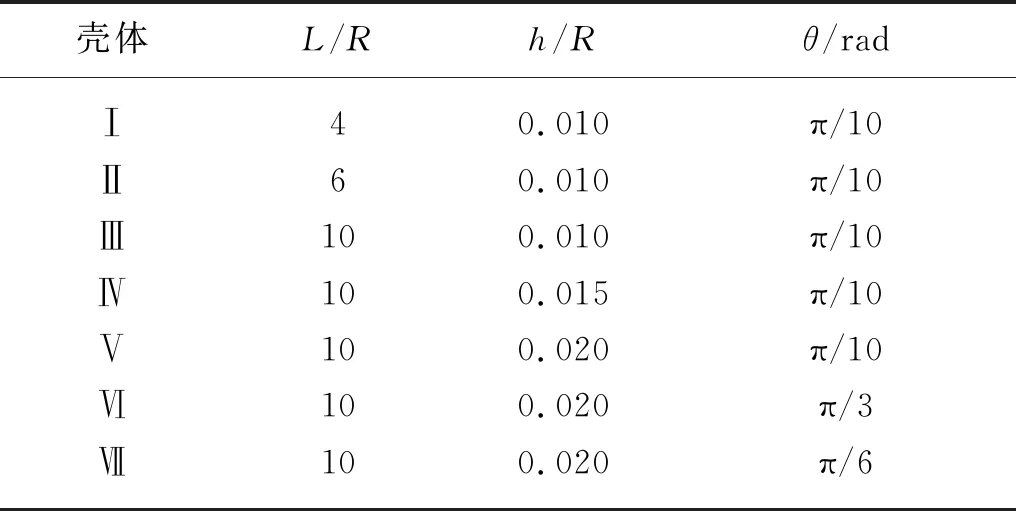
表1 開口圓柱殼的材料參數(shù)與尺寸參數(shù)

由于m、n為偶數(shù)時其對共振響應的貢獻很小，因此本文在算例中僅取對共振響應貢獻較大的前10個模態(tài)進行計算對比。表1中殼體Ⅰ在點(L/2,θ/2)處激勵頻率分別等于前10階模態(tài)頻率時，簡諧激勵在點(L/2,θ/2)處復阻尼系數(shù)分別為0.01、 0.05和0.20情況下的共振響應數(shù)據(jù)，以及級數(shù)解中包含不同模態(tài)階數(shù)的結果與外載荷激勵頻率等于零時(靜態(tài))的結果如表2所示。其中：A表示只考慮激勵頻率等于當前m/n計算得到的固有頻率的響應；B表示N=5、M=15時的響應級數(shù)解，N、M均為位移響應收斂解疊加的項數(shù)；C表示N=19、M=25時的響應級數(shù)解，此時級數(shù)解已收斂，對比計算可知其相對誤差小于0.1%；D表示N=30、M=30時的響應級數(shù)解。靜態(tài)響應與復阻尼系數(shù)之間的關系很小，因此，非靜態(tài)共振響應的峰值隨著復阻尼系數(shù)增加而減小。

表2 開口圓柱殼Ⅰ在點(L/2, θ/2)處的響應

開口圓柱殼Ⅰ在點(L/2,θ/2)處外激勵頻率與m=19、n=1固有頻率相等時的振動響應級數(shù)解與M、N之間的關系如圖2所示，其中，縱軸標題|w(L/2,θ/2)ER/P|×10-3表示無量綱位移響應幅值。

由圖2可知，隨著M、N的增加，響應級數(shù)解值逐漸趨于平穩(wěn)收斂，并且M值對響應級數(shù)解的影響較大，而N對響應級數(shù)解的影響較小。通過計算可知，當N=19、M=25時響應級數(shù)解收斂。

開口圓柱殼Ⅰ、Ⅱ、Ⅲ響應值的變化特性與長徑比之間的關系如圖3所示。由圖3可知：響應值隨外載荷頻率的增加而減小；隨長徑比的增加，共振點的峰值減小，相鄰固有頻率之間的間距減小，共振峰間距減小，而遠離共振峰的響應基本未發(fā)生變化，即長徑比的大小對遠離共振峰的響應影響較小。

開口圓柱殼Ⅲ、Ⅳ、Ⅴ響應值的變化特性與厚徑比之間的關系如圖4所示。由圖4可知：隨著厚徑比的增大，遠離共振點和共振點附近響應值明顯減小；隨著厚徑比的變化，共振點的位置發(fā)生大幅度偏移，并且相鄰共振峰之間的間距隨著厚徑比的增大而增大。

開口圓柱殼Ⅴ、Ⅵ、Ⅶ響應值的變化特性與開口角度之間的關系如圖5所示。由圖5可知：隨著開口角度的增大，一階固有頻率減小，共振峰的峰值增大，相鄰共振峰之間的距離增加；開口角度對遠離共振峰的響應值也有一定的影響，但隨著開口角度的增大，其影響程度逐漸降低。

開口圓柱殼Ⅰ在3種不同復阻尼系數(shù)下，在點(L/8,θ/2)、(L/4,θ/2)和(L/2,θ/2)處施加集中簡諧力的無量綱響應與外載荷頻率系數(shù)的變化關系如圖6所示，其中，每幅圖的上橫軸標記了對應的固有頻率階數(shù)(m/n)的位置。

由圖6(a)可知：當γ=0.01時，m/n=1/1的峰值小于3/1時的峰值；隨外激勵頻率的增加，響應峰值出現(xiàn)波動。這是由開口圓柱殼振動過程中軸向不同位置的響應變化規(guī)律不同所引起的。隨阻尼系數(shù)γ的增大，間距較小的兩個峰值間出現(xiàn)共振峰合并現(xiàn)象。當γ=0.05時，m/n=1/1的共振峰被吸收，無明顯的峰值；γ=0.20時，除第1個共振峰被清晰地顯示出來外，其他的共振峰均明顯受到了抑制，并隨固有頻率的增大逐漸趨于平穩(wěn)。

由圖6(b)可知：當γ=0.01和0.05時，隨外激勵頻率的增加，響應峰值逐漸減小；隨著阻尼的增大，間距較小的兩個峰值間也出現(xiàn)了共振峰合并現(xiàn)象。當γ=0.20時，所有共振峰均無明顯的峰值，且響應隨著固有頻率的增大逐漸趨于平穩(wěn)。

由圖6(c)可知：當γ=0.01和0.05時，隨外激勵頻率的增加，響應峰值逐漸減小；隨阻尼的增大，未出現(xiàn)共振峰合并現(xiàn)象。當γ=0.20時，除m/n=1/1時共振峰明顯的峰值未被抑制外，其余均被抑制，且響應隨固有頻率的增大逐漸趨于平穩(wěn)。

圖6表明，共振峰不僅與固有頻率有關，還與阻尼大小有關，且隨阻尼的增大，共振峰的峰值逐漸減小。當距共振峰較遠時，復阻尼系數(shù)γ=0.01和0.05的響應曲線在非共振位置是無法區(qū)分開的，在這種情況下一般默認選用γ=0.05對應的響應曲線。

5 結 語

本文從圓柱殼的動力學方程出發(fā)，考慮復阻尼的影響，確定了在徑向簡諧激勵作用下，四邊簡支開口圓柱殼在7種不同結構參數(shù)和3種復阻尼系數(shù)的響應，討論結構參數(shù)、材料參數(shù)、激振點與位移響應的關系。主要結論總結如下：

(1) 開口圓柱殼的厚徑比、長徑比和開口角度對振動響應的影響較大，選擇合適的結構參數(shù)對于解決不同工程中的振動問題而言是非常重要的；

(2) 開口圓柱殼的長徑比、厚徑比、開口角度不僅對振動響應幅值有影響，也對振動固有頻率有很大影響，因此在設計時應根據(jù)工況中載荷頻率的范圍來確定開口圓柱殼的結構參數(shù)；

(3) 于同一位置施加載荷的不同則位置的振動響應有所不同，在考慮去除最大共振對于開口圓柱殼的影響時，應考慮殼體不同點的振動響應；

(4) 隨復阻尼系數(shù)的增大，開口圓柱殼的振動響應幅值逐漸減小。