多目標多時間窗車輛路徑問題的鴿群-水滴算法

馬 龍，王春嬉，張正義，董 睿

西安航空學院 經濟管理學院，西安710077

車輛路徑規劃問題是在時間窗約束下實現運輸路徑和作業成本控制的組合優化問題，該問題是由學者Dantzig與Ramser于1959年提出，并在物流運籌學領域獲得廣泛深入的研究。目前對于車輛路徑規劃主要以最小運輸總成本、最短運輸距離和最少配送車輛數目為獨立研究目標，或以這三個獨立研究目標進行兩兩組合，作為優化計算的目標，這樣會使解算目標與實際問題脫節，且問題的求解結果差異較大，特別是針對規模較大的求解問題，傳統的運籌學方法在求解車輛路徑規劃問題最優解時耗時費力[1-2]，因此，國內外學者開始使用基本的人工智能算法或兩種基本算法的混合方法，包括下等雙向搜索算法[3]、禁忌搜索算法[4-5]、量子煙花進化算法[6]、蟻群算法[7-15]、遺傳算法[16-21]、蝙蝠算法[22-23]、狼群算法[24]、混合進化算法[25-27]等。但這些基本算法或混合算法主要以改進基本算法的參數或兩種算法的混合形式，對帶時間窗的車輛路徑問題進行求解。然而，改進后的算法依然存在早熟或無法完全收斂到全局最優解的問題。因此，探索使用互補性較強的兩種智能優化算法，對兩種算法的性能進行互補改進，形成一種新型改進算法是求解帶時間窗車輛路徑問題的熱點研究方向。

智能水滴算法（Intelligent Water Drops，IWD）是學者Hosseini在2007年提出的一種智能算法，該算法通過水滴算子和攜帶泥土量算子來模擬自然界的水系統與河道影響環境而形成的河水迭代流動計算過程。該算法起初在旅行商（Traveling Salesman Problem，TSP）問題[28]、多維背包問題[29]等方面得到應用，隨后，Kamkar等學者率先將該算法應用于車輛路徑問題[30]，且部分學者對該算法進一步改進應用[31-34]，然而，面對多目標多時間窗車輛路徑問題，智能水滴算法及其改進算法依然存在計算速度慢、全局收斂性能差等問題，因此，能否利用一種具備精準搜索方向的智能優化算法對智能水滴算法進行徹底改善，形成一種具有優勢互補的新型智能優化算法解決車輛路徑問題還鮮有研究。

鴿群算法（Pigeon Inspired Optimization，PIO）是受到鴿子的歸巢行為啟發，由學者段海濱等于2014 年提出的新型精準搜索算法，該算法是由兩個精準搜索算子（地圖羅盤算子和地標算子）分階段獨立運行，彌補具有單一算子或復合算子的智能算法搜索不足問題，該算法具有明確的搜索方向和快速的搜索速度、計算精度，且在理論探索和實際應用方面的成果較多。如背包問題[35]、無人機路徑規劃[36]、基本智能算法改進與函數優化求解[37]等。但將基本鴿群算法或單獨利用鴿群算子完全改進智能水滴算法，解決帶有多目標多時間窗的車輛路徑問題的成果還未見報道。

綜上可知，雖然現有的人工智能算法在改進和車輛路徑問題應用方面出現大量的成果，但能使算法在求解多時間窗車輛路徑問題時，能夠滿足收斂速度、計算精度、均衡開發和探索能力的還不夠完善。因此，綜合考慮具有硬時間窗約束的車輛路徑規劃問題的特點，構建多目標多時間窗車輛路徑規劃問題（Vehicle Routing Problem of Multiple-Objectives and Multiple Time Windows，VRPMOMTW）模型，并針對基本智能水滴算法的不足之處，提出求解VRPMOMTW 問題的鴿群-智能水滴互補改進算法（Complementary Pigeon-Inspired optimization and Intelligent Water Drops，CPIIWD），并利用benchmark 函數對CPIIWD 算法進行測試，且將仿真結果與人工免疫系統算法（Artificial Immune System，AIS）、粒子群算法（Particle Swarm Optimization，PSO）、遺傳算法（Genetic Algorithm，GA）的結果進行比較，表明CPIIWD 算法收斂性能要比其他三種算法的性能更好，也是求解VRPMOMTW問題的最佳方法。同時，將VRPMOMTW模型求解結果與遺傳算法[38]、智能水滴算法[33]等結果進行比較，有效彌補了智能水滴算法在多時間窗車輛路徑問題的應用不足，從而強化了人工智能優化算法在車輛路徑規劃方面的應用效果。

1 多目標多時間窗車輛路徑規劃模型

1.1 問題描述

多目標多時間窗路徑規劃問題是通過給一個物流配送中心分配若干輛配送車，為多個服務點提供配送服務，根據不同服務點上的供貨需求量、車輛的最大載重量、服務點與配送中心之間的路徑長度等制約因素，所有服務點上均有相互獨立的服務時間窗。配送車輛為多個服務點提供貨物供應服務，從配送中心出發再回到配送中心形成完整的閉合回路。假設一個服務點由一輛車在規定的時間窗內完成配送服務，且為服務點提供裝卸貨服務的時間窗固定，使用每一輛配送車輛的成本和單位行駛距離成本均固定，單輛車的行駛總距離和行駛時間要求小于給定路線的最長距離和行駛時間。如何使配送總費用最少、配送路徑最短和配送車輛數最少，從而使得車輛配送總成本達到整體最小。為了建模需要，作出如下假設：

（1）車輛由配送中心出發后返回到配送中心。

（2）采用相同型號的配送車輛，且車輛與服務點之間具有一對一和一對多的關系，其服務點需求量小于車輛最大載重量，服務時間恒定。

（3）運輸道路狀況和車流量忽略不計。

（4）配送中心分配的車輛數小于車輛總數，不得重復調度。

（5）車輛到達服務點的時間應在允許的時間窗范圍內波動。

（6）模型的適應度值是以配送車輛的行駛距離和成本為衡量標準。

1.2 變量符號定義

為了準確理解數學模型描述的抽象問題，需要對模型中涉及的變量符號進行定義，并說明符號的含義，如表1所示。

1.3 模型建立

1.3.1 多目標函數

多目標多時間窗車輛路徑規劃問題以最小運輸總成本、最短運輸距離和最少配送車輛數目為優化目標，構建的數學表達式為：

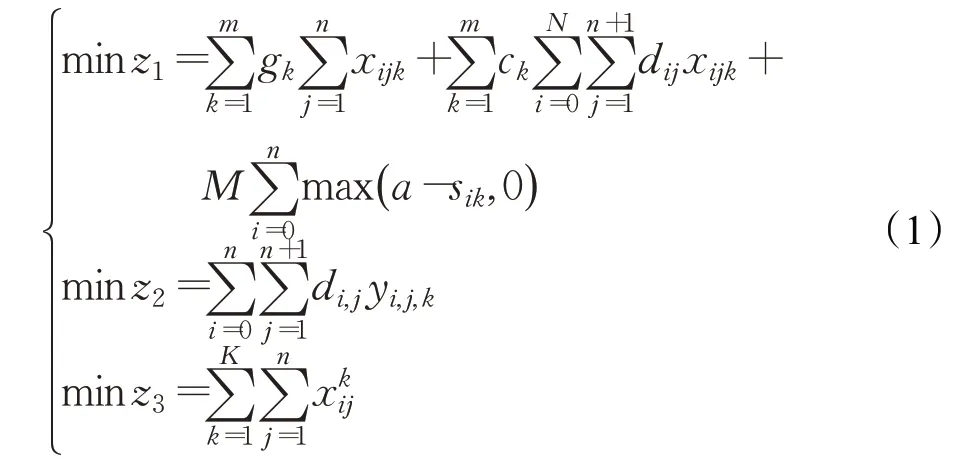
式中，z1中第一項和第二項表示m 輛車的固定運輸成本和行駛距離的成本，第三項表示車輛為服務點提供服務的懲罰成本，即由服務點預訂時間段a 與開始服務時間sik之差構成，M 表示車輛提前與滯后到達的懲罰系數；z2表示車輛k 從第i 服務點出發到達第j 個服務點提供服務的最短運輸距離；z3表示車輛k 從第i 到第j個服務點配備的最少車輛數。

1.3.2 約束條件

（1）車輛出發地點。為了安排最少的車輛數配送貨物，要求每一輛貨車必須從物流配送中心出發，建立的數學表達式為：

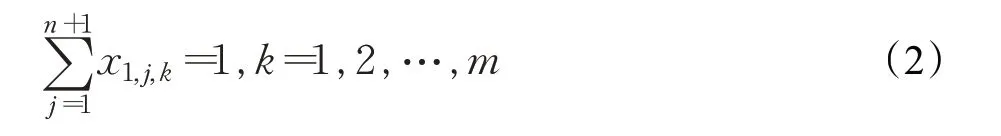
（2）車輛返回配送中心。為了充分利用安排的配送車輛，要求完成配送任務的車輛必須返回配送中心，建立的數學表達式為：

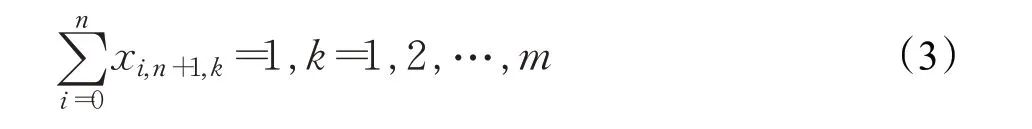
（3）車輛出發的初始地點。配送車輛的出發地點從0點開始，且不作為車輛的返回地點，建立的數學表達式為：

（4）車輛返回地點。配送車輛的最終返回地點需要額外增加返回地點，而不能以原來的出發地點作為返回地點，建立的數學表達式為：

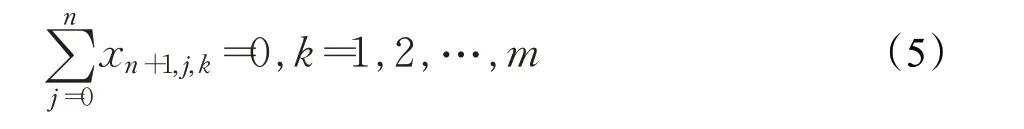
（5）車輛服務點。配送車輛中必須存在唯一車輛與之需求點提供對應的服務，建立的數學表達式為：

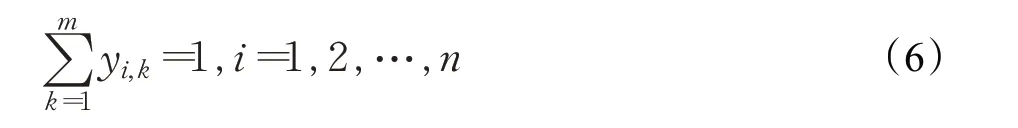
（6）車輛到達服務點。如果恰好存在第k 輛到達第j 個服務點，則該車輛必須為該需求點提供服務，建立的數學表達式為：

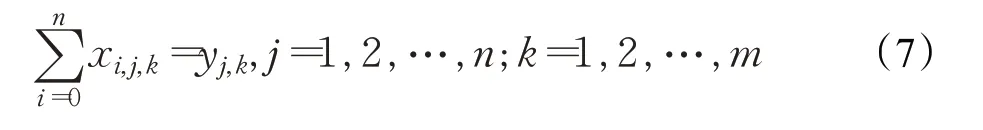
表1 變量符號與含義說明

（7）車輛服務后離開服務點。如果為第i 個需求點配備了第k 輛車，則該車輛服務完成后必須離開第i 個需求點，建立的數學表達式為：

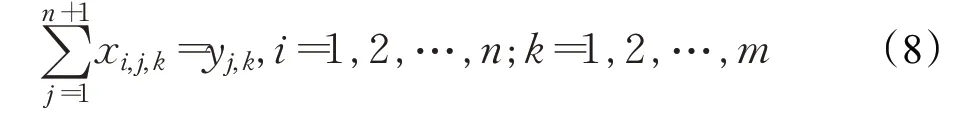
（8）需求總量低于最大裝載量。在物流配送過程中，任何需求點的需求總量必須小于其車輛的最大裝載量，建立的數學表達式為：

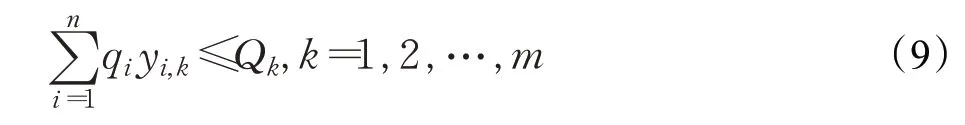
（9）車輛行駛距離限制。在物流配送過程中，任何服務車輛的總里程小于等于最大行駛里程，建立的數學表達式為：

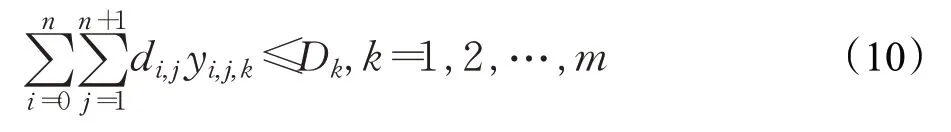
（10）車輛出發時刻限制。在物流配送過程中，要求配送車輛從配送中心點出發的時刻為零，建立的數學表達式為：

（11）車輛到達服務點的時間關系。在物流配送路徑上，任何一輛配送車相繼到達兩個需求點的時刻存在一定的關聯關系，建立的數學表達式為：

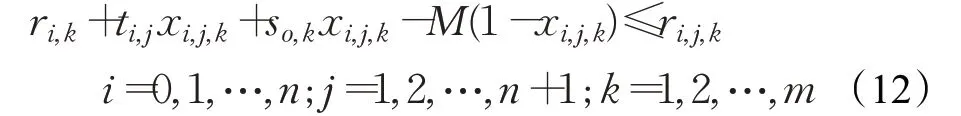
（12）車輛服務時間窗限制。在物流配送過程中，為第i 個需求點在給定的時間窗α 內配備了第k 輛車，則該車輛到達第i 個需求點的時刻需要在時間窗α 的范圍內，建立的數學表達式為：

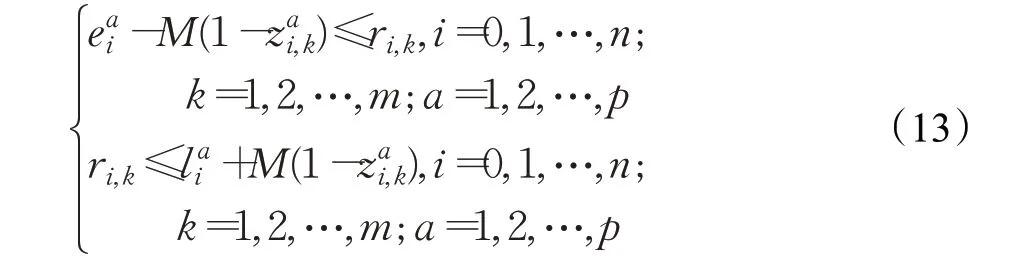
（13）車輛服務完成時間限制。在物流配送過程中，給定第i 個需求點的第k 輛車需要在給定的時間完成服務，建立的數學表達式為：

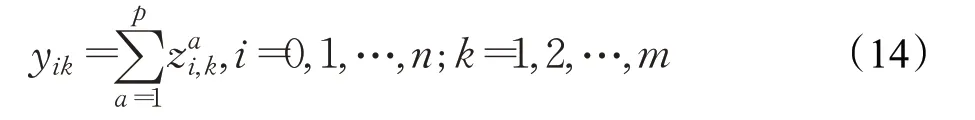
（14）車輛不到達服務點。如果第i 個需求點沒有安排第k 輛車為其提供服務，則該車輛無需到達第i 個需求點，建立的數學表達式為：

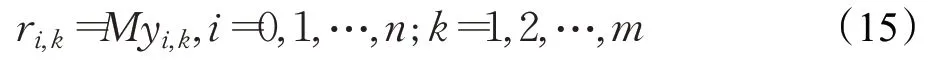
（15）決策變量的取值范圍為：

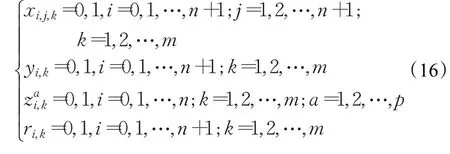
2 多目標鴿群-水滴算法

鴿群算法作為一種典型的仿生進化算法，通過使用兩類獨立搜索算子模擬鴿子的不同搜索方向。在地圖羅盤算子中，如果鴿群偏離目標距離時，經過地磁場形成的腦地圖感知目標方向，靠近目的地后，地磁場與太陽系的作用減弱。如果鴿群臨近目標距離時，熟悉地標的鴿子主要依靠地標算子指引飛行方向，其他鴿子跟隨飛行達到目標地。關于基本鴿群算法的原理可參考文獻[39]。智能水滴算法是在2007 年，學者Hosseini 根據自然界河流中的水流形態和環境變化模擬而提出的智能優化算法，該算法具有水流速度和攜帶泥土量兩類算子，關于水滴算法的原理可參考文獻[28-29]。下面只對利用鴿群算子改進智能水滴算法中，涉及的最優解選擇與存儲機制、適應度函數、改進的水滴流動速度、流動方向和攜帶泥土量以及改進后的智能水滴算法的步驟等進行詳細介紹。

2.1 最優解選擇與存儲機制

利用鴿群-水滴算法求解多目標車輛問題時，算法依然是局部和全局搜索的組合過程。因此，首要解決如何平衡局部與全局搜索獲得的Pareto非最優解的關系，如圖1 所示。根據鴿群經過地圖羅盤算子的方向導引和地標算子的鴿群折半擇優方法獲得每個鴿子的局部最優搜索，搜索到的局部最優解作為水滴流動方向和攜帶泥土量的子代個體。利用存儲池結構來存儲局部搜索到的Pareto非最優解。通過比較存儲池內的解集，如果算法在搜索過程中得到了新的Pareto非最優解，則用其更新存儲池內的一個劣勢解，局部搜索過程完成后，對于智能水滴算法和鴿群算法以及存儲池內所有的解使用Pareto排序和擁擠度選擇機制[40]進行選擇操作，獲得新的迭代搜索群體。

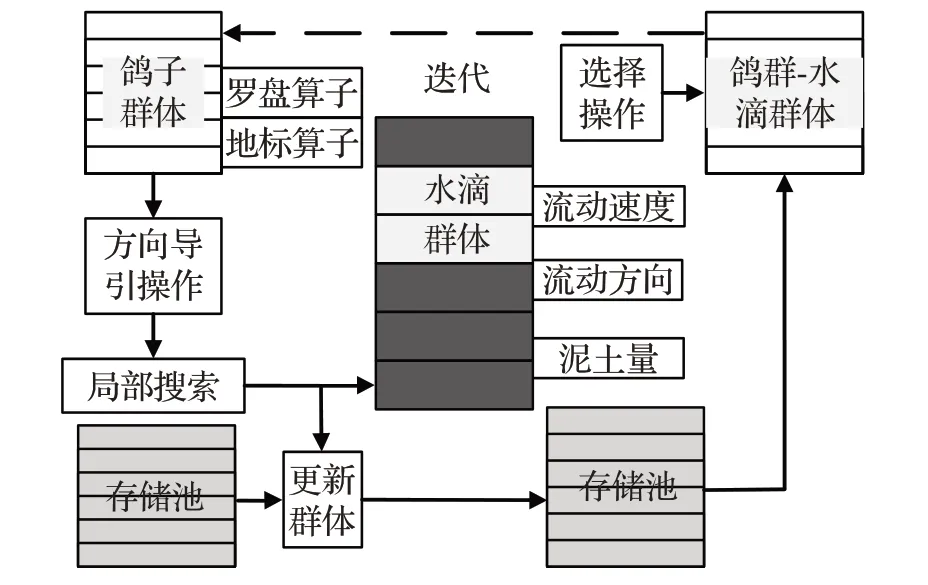
圖1 最優解選擇與存儲機制示意圖

2.2 適應度函數

根據鴿群-水滴互補優化算法的局部和全局搜索機制的差異，在同時考慮三個目標函數時，采用三種不同的適應度函數，分別用于全局最優解和局部搜索最優解的選擇操作。

算法的選擇操作采用Pareto 排序和擁擠度的度量方法[40]，fiti( x )=( rank(x),Crowding-distnce(x) )，其中，rank(x)為Pareto 占優的層級關系，rank(x)＜rank(y)為解x 占優y 。Crowding-distnce(x)為擁擠度距離，距離越大越好。在選擇操作時，對于鴿子群體、水滴群體和存儲池中的所有解按照第一個關鍵字rank(x)升序、第二個關鍵字Crowding-distnce(x)降序排序，然后選擇前N 種群個體迭代進入下一代計算。

在鴿群算法的地圖羅盤算子和地標算子方向的導引下，進行局部搜索，每次搜索均是從候選解的鄰域解列表中選擇一個最好解更新當前解，然后繼續搜索其鄰域，因此可引入Pareto 強度來定義局部搜索的適應度函數[41]：

式中，S( x )表示在存儲池中被x 占優的解的個數，W( x)表示在存儲池中占優x 的解的個數，局部適應度函數反映了解x 在Pareto最優解集中占優強弱程度，如果解x強度大，則適應度高，說明解x 在Pareto 最優解集中處于優勢地位，可在局部搜索過程中優先搜索具有優勢地位解的鄰域。

2.3 利用鴿群搜索算子改進智能水滴算法

智能水滴算法中的水滴通常被抽象為離散化形式，這是因為每一滴水在運動過程攜帶的泥土量不同，且會以攜帶的泥土量大小來選擇流動的方向，這種狀態不利于河道內的水滴快速向最優解靠攏，也不利于攜帶泥土量多的水滴向最優解位置聚集。然而，離散二進制粒子群算法[42]以及利用改進鴿群搜索算子優化的粒子群算法[37]，對于求解種群個體的收斂速度和位置具有良好的效果，本文充分利用離散二進制的位置變化概率和鴿群中的兩類導航算子對智能水滴算法中的水滴流動速度、流動方向和攜帶泥土量算子進行改進，下面分別對智能水滴算法的改進過程進行闡釋。

2.3.1 改進的水滴流速算子

Kennedy與Eberhart提出的離散二進制粒子群算法是對粒子個體進行二進制編碼后，將粒子飛行速度轉化為變換概率[43]，并取得了良好的收斂效果。為了表示水滴速度值為二進制位取1的概率，本文將水滴流動速度值映射到區間[0，1]，映射的方法一般利用Sigmoid 函數，其數學表達式為：

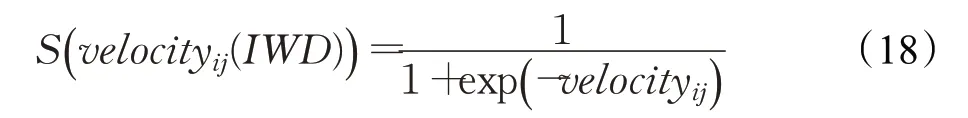
式中，S( velocityij(IWD) )為水滴移動位置x( i,j )取1 的概率，水滴通過式（19）改變對應位值：

式中，rand( )表示在[0 ,1] 區間內產生的隨機數，為了避免S( velocityij(IWD) )過度趨近0 或1 的邊緣，使用參數velocitymax表達為水滴流動的最大速度值，用于限制水滴流動速度velocityij(IWD) 的取值范圍，即velocityij(IWD)∈[- velocitymax,velocitymax] ，水滴流動速度最終限制了x( i,j )取0或1的概率。

智能水滴算法中的水滴經過離散化處理后，水滴流速快慢與攜帶的泥土量多少直接相關，特別是水滴流動過程中席卷的泥土量越大，則水滴的流速必會減慢，因此，利用鴿群算法中的地圖羅盤算子對水滴的流速進行改進，改進后的數學表達式為：

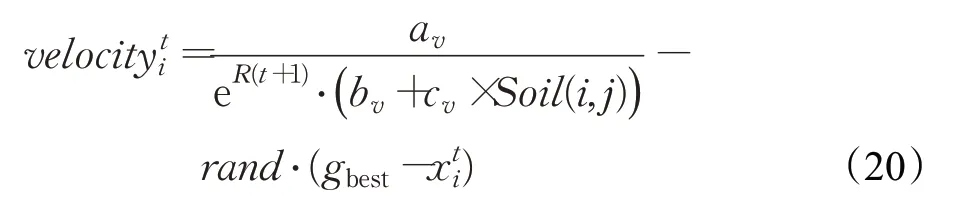
2.3.2 改進的水滴流動方向

為了說明離散化水滴攜帶大量泥土而選擇最優的流動方向，水滴位置x( )i,j 變化概率是關鍵，根據文獻[43]中提出的位變化概率，對此進行分析，根據式（19），水滴流動軌跡是一種根據攜帶泥土重量交替選擇概率，設為水滴在第t 次從位置i 流動到位置j 的速度，第t 次位為1的概率是，而且位為0的概率是1，此外，如果第t-1 次位值已成為0，則第t 次變化的概率為，同樣，如果第t-1 次位值已成為1，則第t 次變化的概率為，而第t-1 次位值是0 的概率為，第t-1 次位值是1 的概率為。則第t 次位的變化概率p( t )為：

根據式（18）的結果，可得到如下的數學表達式：

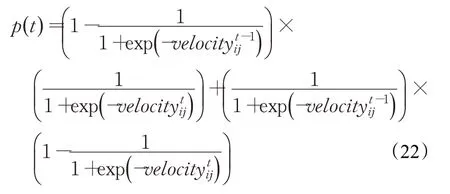
根據水滴攜帶泥土重量的大小，選擇流動概率，但流動方向還與地標指引方向有關，因此，利用鴿群算法中的地標算子改進水滴流動方向，其數學表達式為：

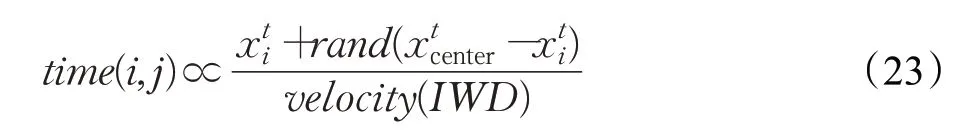
式中，xcenter為引導水滴流動的中心位置；其余變量的符合含義與式（20）一致。

2.3.3 自適應變鄰域擾動攜帶泥土量算子

在以上改進的IWD 算子中，只是對水滴流經河道內的水滴速度和方向進行改進，并未對整個河道內的泥土量變化情況進行考慮，為了提高算法開發和探索能力，提出自適應變鄰域擾動策略對水滴攜帶泥土量進行干擾，增加算法的全局收斂能力。自適應變鄰域擾過程，如圖2所示。

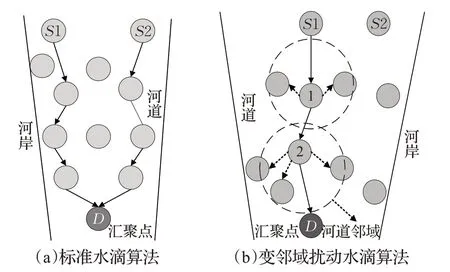
圖2 自適應變鄰域擾動過程

根據圖2可知，在IWD水滴算法中，水滴位置S1 和S2 向目的地匯聚過程中，河道中央的水滴會不斷對鄰域位置上的水滴進行擾動，且會根據河道中的泥土量Soil(IWD)取值實時更新，并根據河道鄰域內的水滴位置k 與匯聚點D 的間距大小來更新，如果間距小，則無需更新河岸edge( )k,j 的泥土量，否則位置k 上的水滴將產生新攜帶的泥土量Soil(IWD′)，該水滴個體攜帶的泥土量Soil(IWD)初始值設定為0，水滴流速velocitykD(IWD′)的初始值設定為Initvelocity，其攜帶新泥土量的水滴速度和位置的更新表達式為：

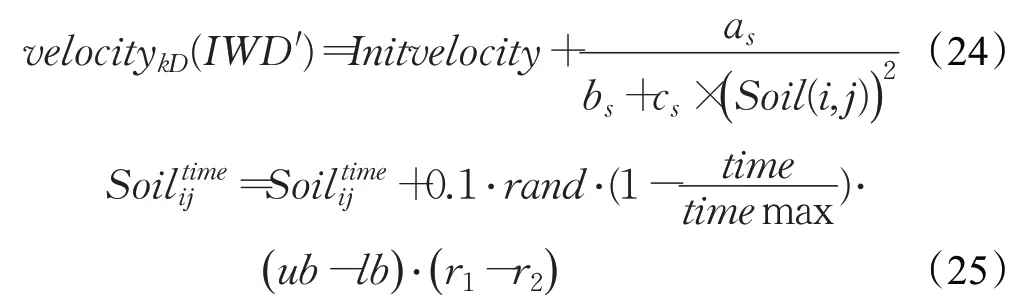
由此可推算出河岸edge( k,j )上的泥土量Soil(IWD)參數變化表達式為：

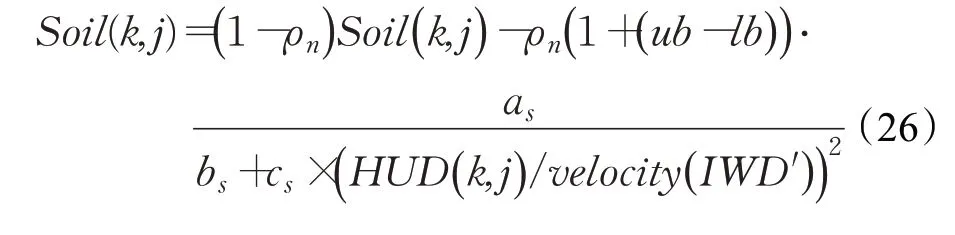
2.4 改進的智能水滴算法步驟

標準智能水滴算法的兩類算子在迭代計算時，通常根據水滴流動過程中攜帶的泥土量來確定水流速度和移動方向，且攜帶的泥土量也會隨著水流速度發生變化，這樣算法在局部空間搜索計算時，由于某段河道內水滴攜帶泥土量較多，算法會陷入早熟收斂狀態，然而鴿群算法中的兩類獨立運行算子能夠根據地圖羅盤和地標的導引，可較好地指明個體鴿子的飛行方向和飛行速度，因此，本文利用鴿群算法中的地圖羅盤算子和地標算子以及自適應擾動策略分別對智能水滴算法中的流動速度、流動方向以及水滴攜帶泥土量進行改進，設計出引入鴿群搜索算子的智能水滴算法，較好地克服標準智能水滴算法在車輛路徑問題求解方法的不足，算法的具體計算步驟如下：

步驟1 設置算法參數；最大迭代計算次數tmax；鴿子個數m；水滴個數N ；水滴流速參數av、bv、cv；泥土更新參數as、bs、cs；局部泥土更新系數ρ0、ρn；起止位置的初始泥土量

步驟2 初始化所有水滴的參數；設置算法的動態參數；水滴初始狀態集合S( )IWD =?，水滴初始速度、水滴初始攜帶泥土量Soil(IWD)以及初始攜帶重量。

步驟3 選擇水滴局部更新信息；水滴根據流動路徑上的泥土量大小，按照式（21）概率大小選擇流經下一節點，根據被選擇節點更新水滴的局部信息，按照式（24）～式（26）更新水滴的局部信息。

步驟4 根據式（24）、式（26）分別對水滴的流動速度和攜帶的泥土量進行更新。

步驟5 條件判斷；如果河道內所有的水滴都會收斂至同一路徑或達到最大迭代計算次數，轉到步驟6，否則轉到步驟3。

步驟6 保存最優解與最優值，求解計算結束。

3 多目標多時間窗車輛路徑模型處理方法

多目標優化問題通常采用懲罰函數與帕累托最優解集進行約束條件處理，且這兩種方法有著不同的特點。下面從懲罰函數和帕累托最優解集兩個方面，對本文的多目標車輛路徑模型的處理方法進行探討分析，并提出多目標優化與懲罰函數的混合策略。

3.1 模型處理策略

多時間窗車輛路徑規劃問題可使用有向有環圖來表達，假設圖G=(V ,E )，V={0 ,1,2,…,n} 表示車輛配送中心0 與服務點i=1,2,…,n，E 表示車輛節點之間的路徑集合。同時，使用水滴抽象表示每一輛車，水滴多次經過配送中心0，一次經過服務點，形成完整的流動路徑過程恰好為VRPMOMTW的解。求解一次迭代結束后，可在每個水滴流經的完整路徑中搜索出最優路徑，利用該最優路徑不斷更新各個水滴節點之間的泥土量與全局最優路徑，然后迭代到下一步迭代過程，直到達到算法的最大次數或期望的優化路徑。

3.1.1 多目標函數的懲罰處理策略

多目標車輛路徑規劃問題涉及三個以上的目標函數和多類復雜的約束條件，該類問題的求解較為復雜，為了簡化問題的求解難度，利用罰函數法[44-45]和理想點方法[46]分別對模型中的約束條件與多目標函數進行簡化處理。根據理想點法，將最小運輸總成本、最短運輸距離和最少配送車輛數目的多目標轉化為單目標問題，多目標車輛路徑規劃模型可轉化為以下形式：

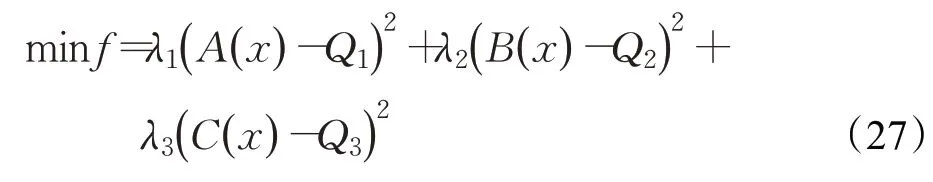
式中，Q1為A( x )的效用函數，取值為利用線性規劃方法求解該問題的上界值；Q2為B( x )的效用函數；Q3為C( x )的效用函數，由約束違反度函數的特性，且取值為零；λi為第i 目標函數的權重，且∑λi=1，這種方法只能找到部分Pareto 最優解，為了找到更多的Pareto 最優解，可利用Pareto排序法確定各目標函數的權重系數。

3.1.2 多目標優化與懲罰函數的混合策略

通常采用懲罰函數法和Pareto 最優解集對多目標函數問題進行處理，但根據上述懲罰函數處理方法可知，雖然懲罰函數的選取具有一定的主觀性，但根據Pareto 優超的定義和關系[47]，Pareto 最優解集并非適用于所有個體，根據需要引入偏好程度才更為有效，如圖3所示，在Pareto 最優解集中包含3 個依次排列的非劣個體A、B、C，假設只有個體A 距離可行域較近，而個體B與C 距離可行域較遠，所以A 是需要提取的重要信息。另外，不可行解是無法超越Pareto 可行解，這是因為全局最優點落在邊界點上，且算法進入搜索后期會丟棄不可行解。因此，基于Pareto最優解集的多目標優化方法往往忽視了偏好程度，且引入偏好的簡便方法是懲罰函數法。因此，本文提出多目標優化與懲罰函數混合方法，首先為了權衡目標函數與約束條件方程G(x)的標準變化，將從Pareto 最優解集中選擇個體的搜索偏好，找出群體中的最大和最小目標函數值，然后對每個目標函數值和約束條件的程度進行歸一化處理，這樣處理的目標函數具有降維特征，且可以比較Pareto最優解集中的個體，根據偏好選擇個體。同時，在算法搜索初期存在少量可行解，通過引入懲罰函數，可以引導算法盡早進入可行域。另外，優化過程中，懲罰系數會依據群體狀態自動調整，當群體的可行解比例p ＞0.5 與懲罰系數ρ ＜1 時，可開發出目標函數與約束程度較小的不可行解。

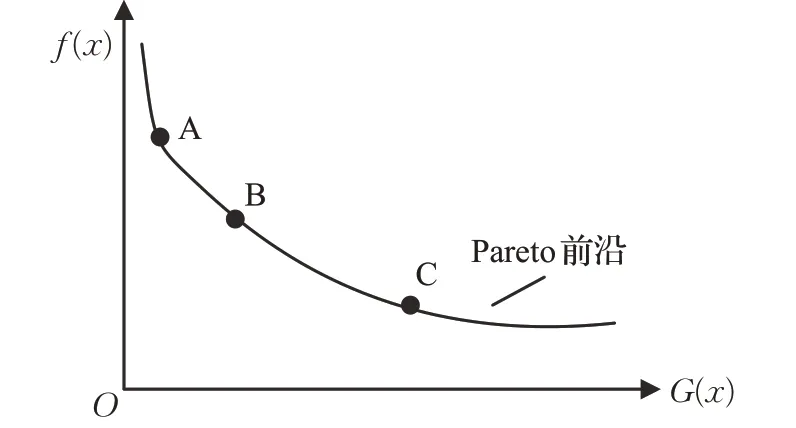
圖3 Pareto最優解集中的非劣解示意圖

3.1.3 權重系數處理策略

在問題可行域上對各個目標函數zi( x )進行極小化處理，計算極小值點xi，得到：

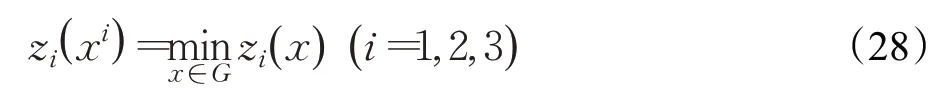
利用算術平均法計算i 個分目標函數的極小點的相對離差、為了避免各個分目標函數值離差過大而影響權重系數的選取，對求解的相對離差做無量綱化處理。

同時，利用算術平均法計算出第i 個分目標函數的極小點的平均相對離差，得到：

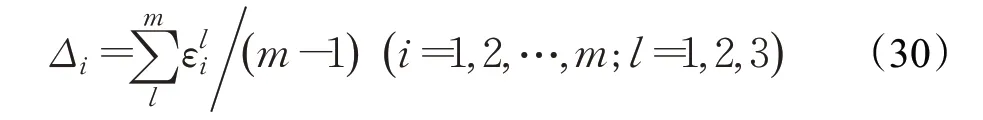
顯而易見，為了使權重系數規范化，當Δi＞0 時，假設Δi1≥Δi2≥…≥Δis，且Δis∈{ Δ1,Δ2,…,Δm} ，選取如下式作為各分目標對應的權系數：

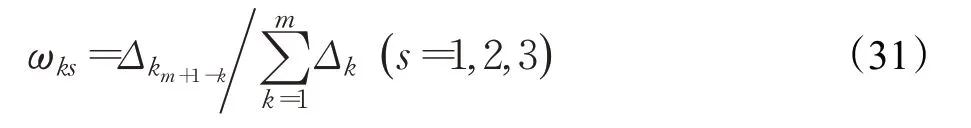
根據上述分目標函數與權重系數的確定方法，構建的多目標車輛路徑規劃模型的數學表達式為：

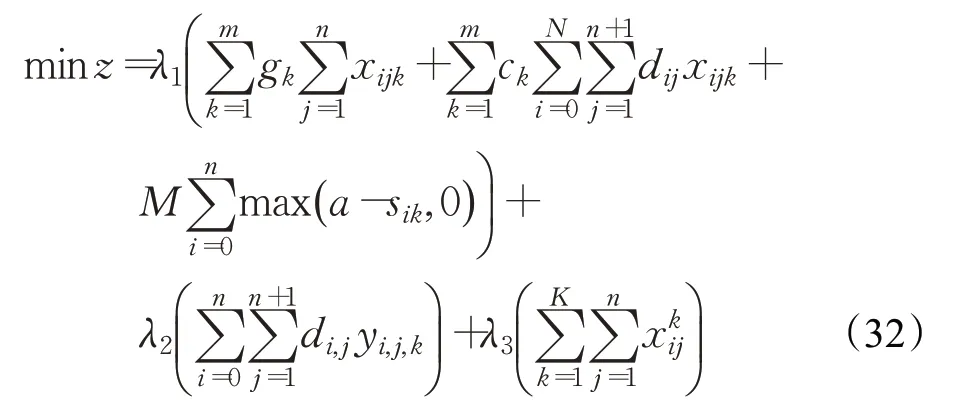
式中，變量的含義與式（1）、式（27）的一致。

3.1.4 約束條件處理策略

多目標窗車輛路徑規劃問題是帶有多種約束條件的復雜問題，采用罰函數法[44-45]將模型中的部分約束優化問題處理為無約束優化問題，由此對式（2）～式（15）中的約束條件處理如下：

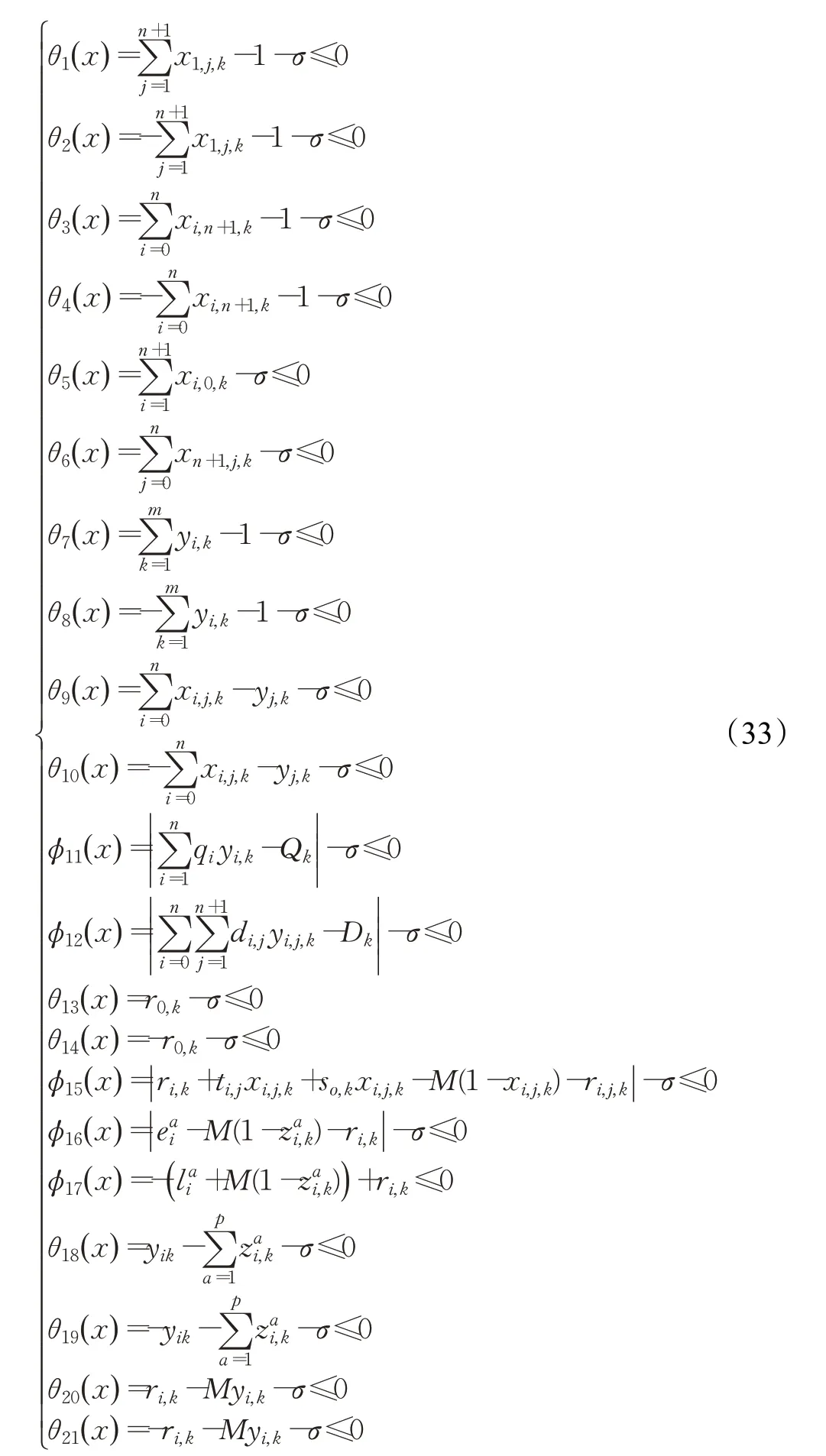
式中，φi( x )為不等式約束條件；θi( x )為等式約束條件；σ 表示等式約束的懲罰因子；表明優化后的車輛配送成本應允許在[- σ,σ ]范圍內波動，通常σ 取很小的值。

3.2 模型求解步驟

步驟1 輸入初始靜態變量；服務點與配送中心集合D；服務點個數n；配送中心點0，服務點i 的需求量為qi,多時間窗t=1,2,…,p；服務時間sti,i=1,2,…,n；服務中心至服務點的距離矩陣為d；車輛的單位運行成本c；車輛固定成本g；車輛行駛速度v；車輛的最大載重量Qmax；車輛在服務點與配送中心之間的行駛時間矩陣T ；最大迭代次數tmax；水滴數N ，水滴流動更新速度參數av、bv、cv，泥土攜帶量更新參數as、bs、cs，局部泥土量更新權值a，全局泥土量更新權值β，服務點上的初始泥土量InitSoil,水滴的初始流動速度InitVelocity,攜帶泥土量初始矩陣

步驟2 輸入初始動態變量；初始化已訪問節點集Visitnode 為空集；未訪問節點集初始化為Novisitnode={0 ,1,2,…,n} ；水滴（車輛）從配送中心出發攜帶泥土量初始化為InitSoil=0；水滴（車輛）從配送中心出發的流動速度初始化為InitVelocity=0；水滴（車輛）從配送中心出發的載重量初始化為Qmax=0；水滴從配送中心出發的開始時間為t=0。

步驟3 根據路徑規劃模型的約束條件，隨機選取水滴的初始訪問節點，以時間窗動態更新水滴訪問節點列表Visitnode( IWD )和未訪問節點列表Novisitnode( IWD )。

步驟4 根據時間窗上未訪問節點Novisitnodei的需求量，確定水滴移動訪問節點集合DV ；如果未訪問節點集合NDV 不符合容量和時間窗約束，水滴（車輛）返回配送中心0，初始化水滴對應的動態變量，形成一輛配送車輛的路徑；如果未訪問節點集合NDV=?，水滴（車輛）返回配送中心0，形成水滴（車輛）的完整訪問路徑，該路徑對應VRPMOMTW問題的可行解TIWD。

步驟5 利用多種節點選擇方法，在水滴到達節點的服務概率與距離以及泥土量中加入重要度因子，計算水滴訪問列表的概率p( t )，確定從當前節點i 到NDV 中的下一個服務點j 的概率，如下式：

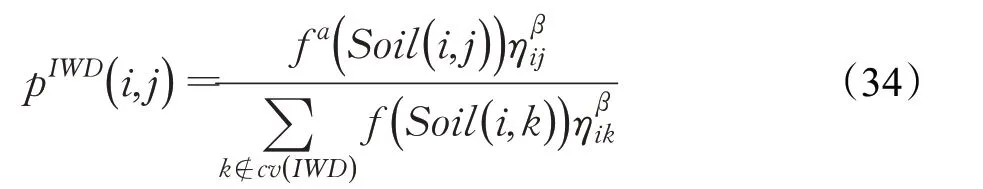
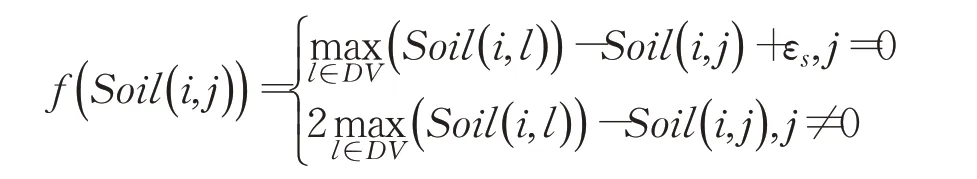
εs為較小的整數，且εs=0.01。

步驟6 根據訪問節點集合DV 中每個節點對應的概率，采用式（22）選擇下一個被訪問節點。并將被訪問服務點j 列入已訪問節點集合中，并修改當前水滴對應的已訪問節點集合、訪問順序和未訪問節點集合。

步驟7 根據式（24）、式（25）、式（26），分別對水滴（車輛）的流動速度velocityij(IWD) 、攜帶泥土量Soil(IWD)和路徑滾動泥土量進行更新；其中，為了避免算法早熟問題，路徑泥土攜帶量需要在Soil( i,j )∈[min Soil( i,j ),max Soil( i,j )]之間變動，且min Soil( i,j )與max Soil( i,j )的計算表達式如下[34]：

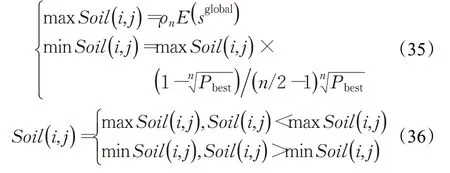
式中，Pbest=0.5，n 表示服務點數；表示當前局部最優解。

步驟8 根據步驟3 中計算的完整訪問路徑TIWD，并假設運輸總成本cost(TIWD)，則搜索出目標函數中最小平均可行解作為模型的最優解TTB。

步驟9 根據當前迭代計算得到的最優解TTB，并將更新后的泥土量矩陣作為下次迭代計算的初始泥土量矩陣，其計算表達式為：

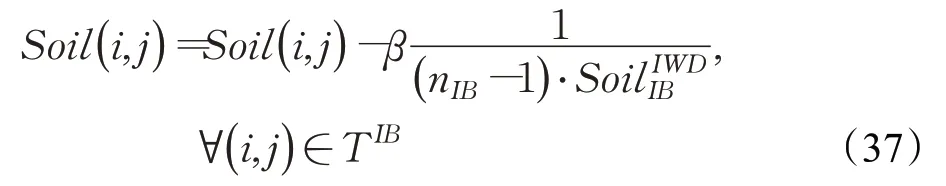
其中，nIB表示當前迭代計算路徑上的服務節點數，表示最優路徑上水滴（車輛）攜帶的泥土量。

步驟10 更新模型計算的全局最優解：

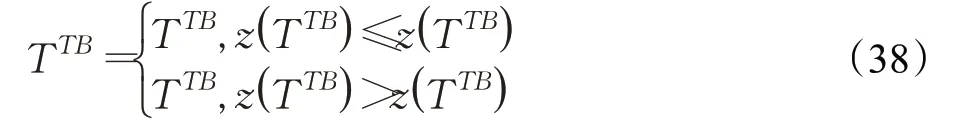
步驟11 更新迭代計算次數ti=ti+1，若ti＜tmax，則轉入步驟2，否則，如果ti=tmax，則將最優解fmin作為VRPMOMTW的最優解，并輸出計算結果。

4 實例仿真與結果分析

4.1 算法性能測試函數

為了驗證所提CPIIWD 算法的性能，以文獻[37]中的6 個經典函數為例，對算法性能進行仿真測試，其函數的具體形式如下：

（1）Sphere"s function

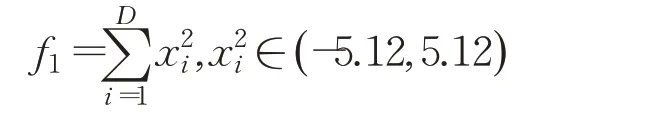
（2）Rosenbrock"s function

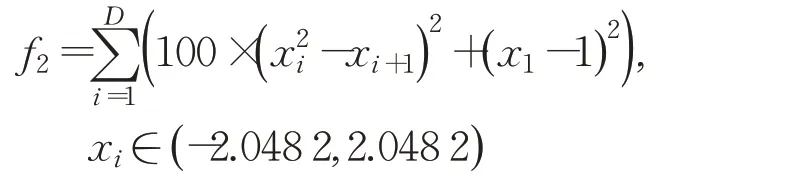
（3）Griewank"s function

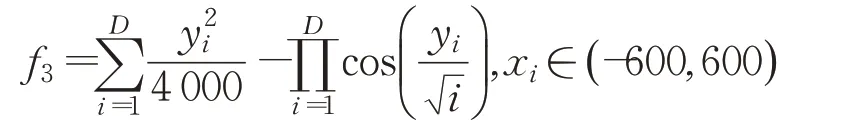
（4）Ackley"s function

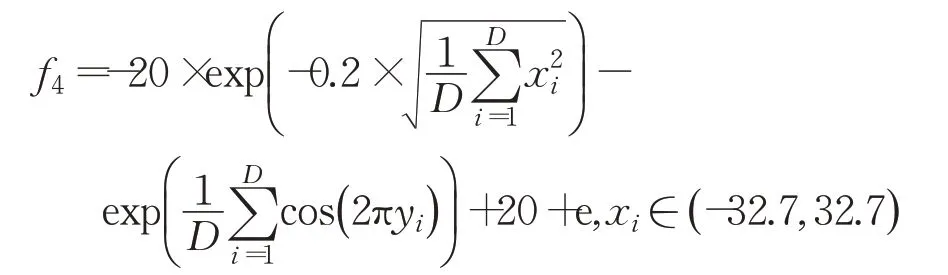
（5）Penalized function

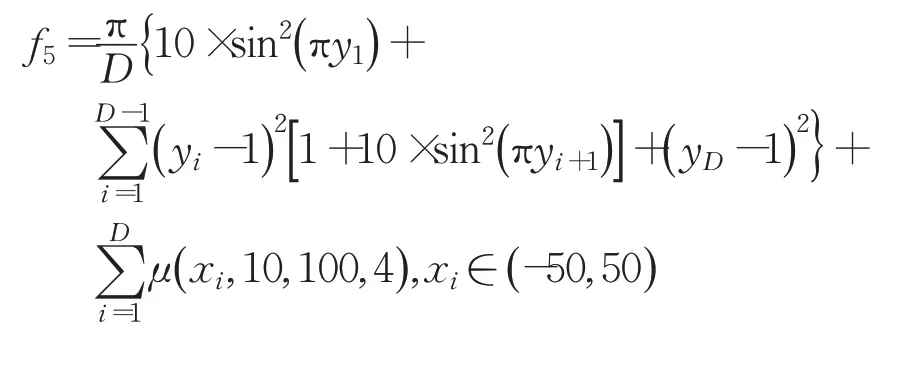
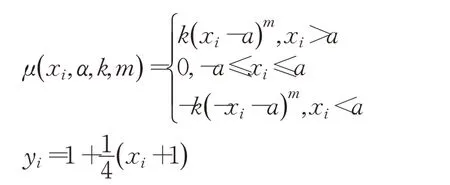
（6）Shifted Griewank

4.2 實例數據來源

為了進一步驗證本文提出的VRPMOMTW 的穩定性與算法的可行性，選用文獻[33，38]中的案例，利用CPIIWD 算法對VRPMOMTW 進行優化求解，并與文獻[33，38]中的求解結果進行比較。

實例1 某物流配送中心在不同時間窗內和服務時間長度，為10個需求量不同的客戶提供物流配送服務，其配送中心與需求服務點的距離和服務時間如表2、表3所示。

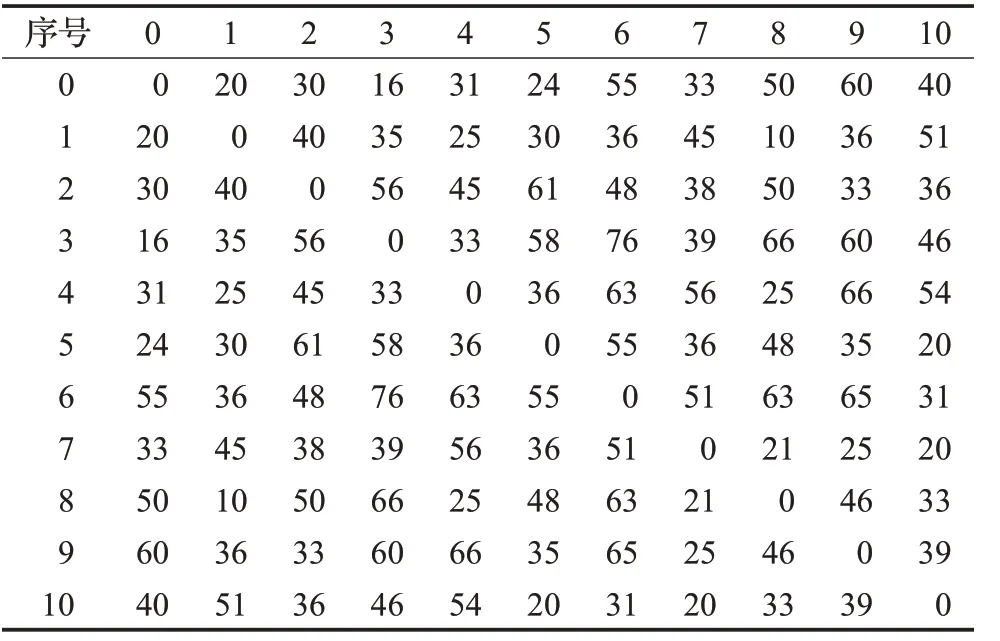
表2 配送中心與服務點之間的距離 km

表3 多時間窗的服務點需求量與服務時間

實例2 某配送中心的車型相同，配送服務需求點為20，配送中心位置為（0，0），每個需求點的位置坐標、需求服務量和時間窗等信息如表4所示。

4.3 模型與算法參數設置

實驗環境：Inter CoreTMi5-2450MCPU@ 3.2 GHz，內存為4 GB，Window7 操作系統，MatlabR2015a 版本，四種算法經過反復迭代計算后，選取如下參數后，計算結果較為理想。

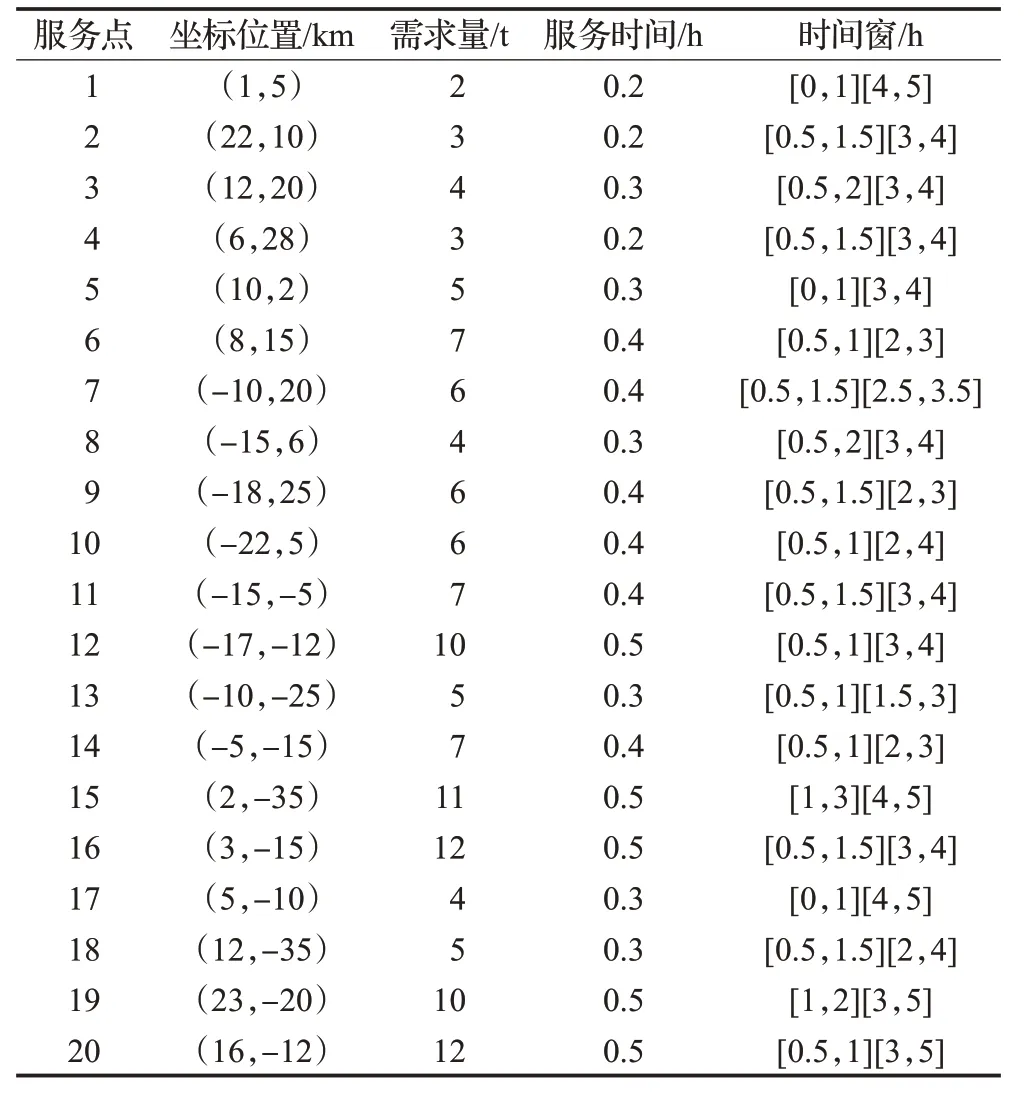
表4 服務點位置、需求量、服務時間、時間窗數據

算法參數：（1）人工免疫系統算法[48]。抗體數n=30,交叉概率pc=0.6，變異程度pm=0.3，淘汰率pe=0.3，濃度閾值Tc=0.3，抗體親和力閾值Tac1=0.75，記憶細胞親和力閾值Tac2=0.8，記憶細胞數量Nm=5，最大迭代次數tmax=500。

（2）粒子群算法[37]。種群規模S=300,K=3,維度D=100,最大迭代次數tmax=500。

（3）遺傳算法。種群規模N=300 ，交叉概率pc=0.7，變異概率pm=0.3，最大迭代次數tmax=500。

（4）鴿群-水滴算法。水滴數NIWD=100，水滴流動更新速度av=1,bv=0.1,cv=1，泥土攜帶量更新參數as=1,bs=0.1,cs=1，局部泥土量更新參數a=1，全局泥土量更新參數β=1，服務點上的初始泥土量InitSoil=2 000，初始流動速度InitVelocity=100，最大迭代次數tmax=500，水滴流動方向的羅盤導航因子R=0.9，局部泥土更新系數ρ0=ρn=0.5。

模型參數：車輛最大載重量Qmax=90 t ，車輛固定成本g=50 元，車輛行駛單位成本ck=20 元，車輛的平均行駛速度v=50 km/h，車輛在配送中心與服務點之間的行駛時間tij=dij/50 h。

實例參數：實例1中，水滴數NIWD=100，水滴流動更新速度av=1,bv=0.1,cv=1，泥土攜帶量更新參數as=1,bs=0.1,cs=1，局部泥土量更新參數a=1，全局泥土量更新參數β=1 ，服務點上的初始泥土量InitSoil=2 000 ，水滴的初始流動速度InitVelocity=100，最大迭代次數tmax=100，水滴流動方向的羅盤導航因子R=0.9，局部泥土量更新系數ρ0=ρn=0.5。

實例2 中，水滴數NIWD=200，水滴流動更新速度av=1 000,bv=0.1,cv=1 ，泥土攜帶量更新參數as=1 000,bs=0.1,cs=1，局部泥土量更新參數a=0.9，全局泥土量更新參數β=0.9 ，服務點上的初始泥土量InitSoil=2 000 ，水滴的初始流動速度InitVelocity=100，最大迭代次數tmax=800。

4.4 仿真結果與分析

4.4.1 算法性能測試結果與分析

根據表5 的仿真結果可知，四種算法分別經過500次的迭代測試后，發現除了Rosebrock 函數和Penalized函數無法收斂到理想值，其余4種函數幾乎可收斂到理想的函數值。雖然AIS算法的收斂計算時間明顯減少，但AIS算法的收斂能力較弱，這是因為AIS算法中保存在記憶庫中的抗體數較少時，降低了記憶細胞的搜索能力。另外，經過Penalized 函數的仿真結果發現，雖然GA和CPIIWD收斂計算的結果幾乎接近理想值，但GA算法的求解速度慢于AIS算法的求解速度，這是因為該函數是分段函數，算法在收斂計算時的參數設置的不同而造成的差異。同時，使用PSO算法仿真測試的多維單峰和多峰函數收斂計算時間較長，而采用CPIIWD算法的收斂計算時間明顯減少，收斂效果要優于其他3種不同的算法，這說明鴿群-水滴互補優化算法在多維函數優化方面的改進效果要比單個人工智能算法的效果更好。

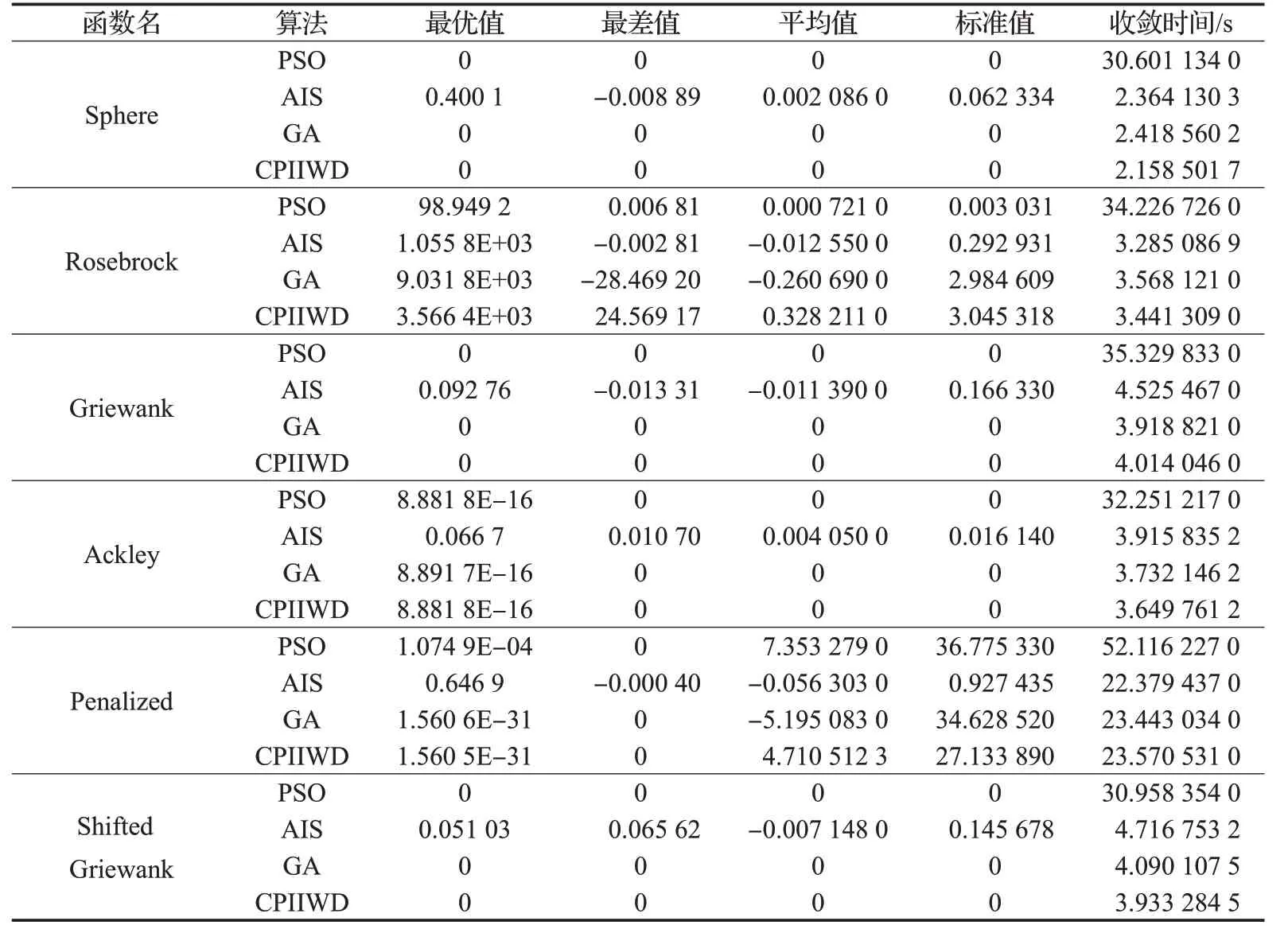
表5 四種算法的計算結果

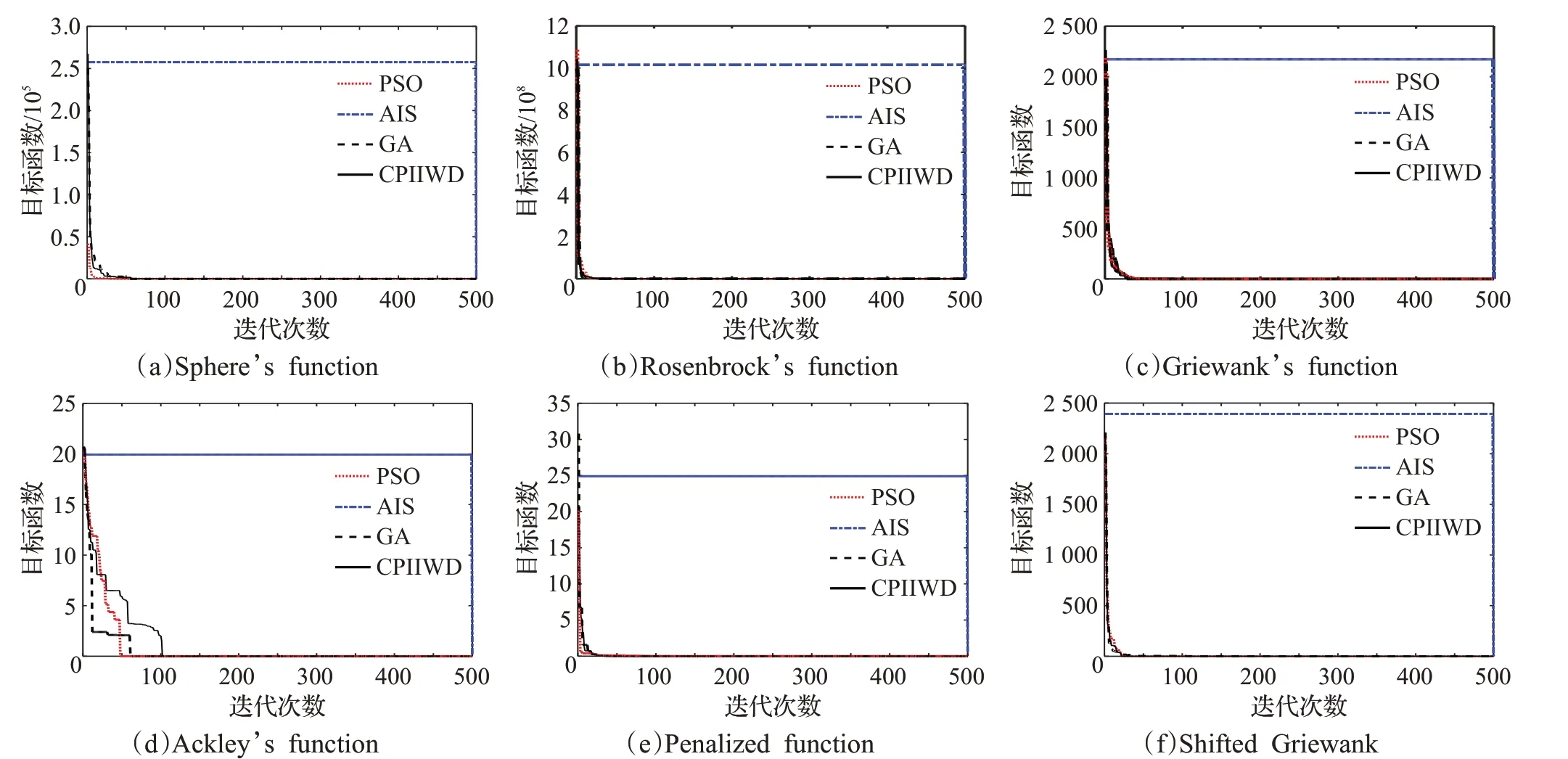
圖4 四種算法的仿真收斂曲線

根據圖4的收斂曲線清晰看出，提出的鴿群-水滴互補優化算法由于引入精準的鴿群算子和多目標種群初始化方法，使得智能水滴算法在計算復雜多維函數時，可逃逸局部最優搜索空間，并在短時間內快速向全局最優解方向收斂。特別是AIS算法在6種不同函數上的收斂結果都不理想，且計算時間要比CPIIWD算法的計算時間長，但從部分函數也可看出，CPIIWD 算法在某些測試函數上也不能完全表現出最優性能，這是因為對水滴算法的初始參數選取和固有的弊端總會導致部分搜索計算效果較差，但從總體上來看，CPIIWD 算法要明顯優于其他3種算法，這是因為利用鴿群搜索算子對水滴算法中的算子互補改進后產生的明顯效果。

4.4.2 模型求解結果與分析

通過算例1 中的數據源與處理后的約束條件（33）和目標函數（1）的編程，利用CPIIWD 算法求解出本文最小運輸總成本為6 705元、最少配送車輛數為3輛，最短配送路徑如圖5所示。

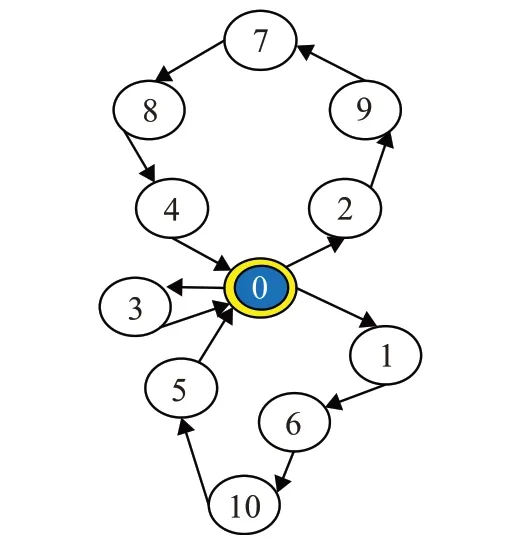
圖5 3輛車的最短配送路徑示意圖

根據圖5 的車輛配送路徑分布結果可知，實例1 中的車輛從物流配送中心出發，經過不同時間點和服務點后，3輛配送車行經最短運輸距離，最終返回配送中心，符合物流車輛配送作業的基本要求。

為了進一步驗證本文CPIIWD算法求解VRPMOMTW問題的可行性，分別利用遺傳算法、基本智能水滴算法和CPIIWD算法對車輛路徑問題進行解算，在實例1中，三種不同的人工智能算法經過100次的迭代計算后，其收斂計算結果的曲線如圖6所示。

根據圖6中的收斂曲線可知，經過三個不同的人工智能算法仿真計算后，遺傳算法經過23 次迭代后獲得了問題的全局最優解，基本智能水滴算法經過19 次得到了全局最優解，而CPIIWD算法經過16次獲得了問題最優解，這說明經過鴿群搜索算子對水滴算法的互補改進后，模型的求解效果要明顯優于其他兩種算法，且使用該算法求解的最小運輸總成本要比其他兩種算法少，為物流企業節約不少的運輸費用。

表6 三種不同算法的求解計算時間比較

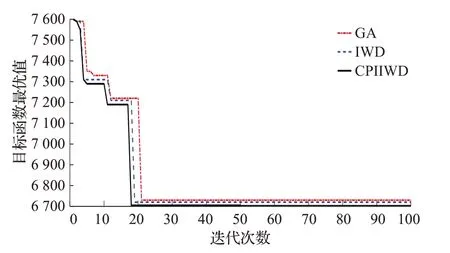
圖6 三種算法的收斂計算過程

為了再次驗證本文算法求解效果，通過對3種不同算法的尋優次數、最少迭代次數和計算時間等進行比較，如表6所示。

通過表6的計算結果可知，三種算法在相同的數據源和模型參數設置下，基本智能水滴算法的尋優次數為96，遺傳算法的尋優次數為30，而CPIIWD算法為28，這是因為鴿群算子具備精準的羅盤算子和地標算子，使改進后的水滴算法的計算時間和迭代次數明顯減少，但該算法得到的最差值要遜色于其他兩種算法，說明根據文獻[37]中的原理，任何算法不是萬能的，不可能在各個方面都能表現出良好的效果。

通過實例2 中的數據來源與模型參數設置，利用CPIIWD 算法對多目標多時間窗車輛路徑問題進行仿真計算，其20個服務點的最優配送路徑示意圖如圖7所示，最小成本的收斂計算結果如圖8 所示，并對20 個服務點的車輛路徑距離進行優化計算，如圖9所示。

圖7 20個服務點的最優配送路徑示意圖

根據圖7中的配送路徑分布結構圖可知，物流服務車輛經過不同的需求服務點后返回服務中心，且經過CPIIWD算法的求解計算后，20個服務點上需要最少分配4輛相同型號的車輛。

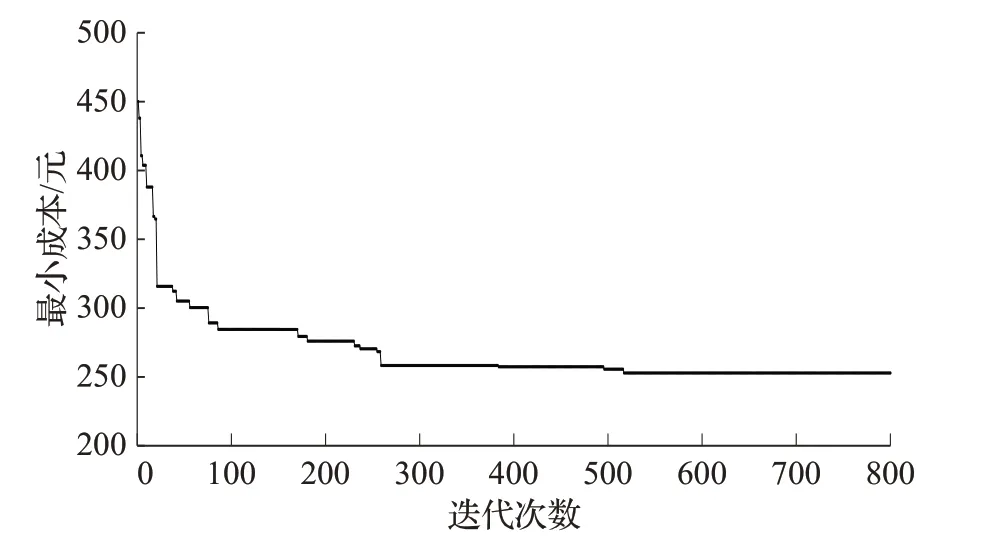
圖8 鴿群-智能水滴算法的收斂計算過程

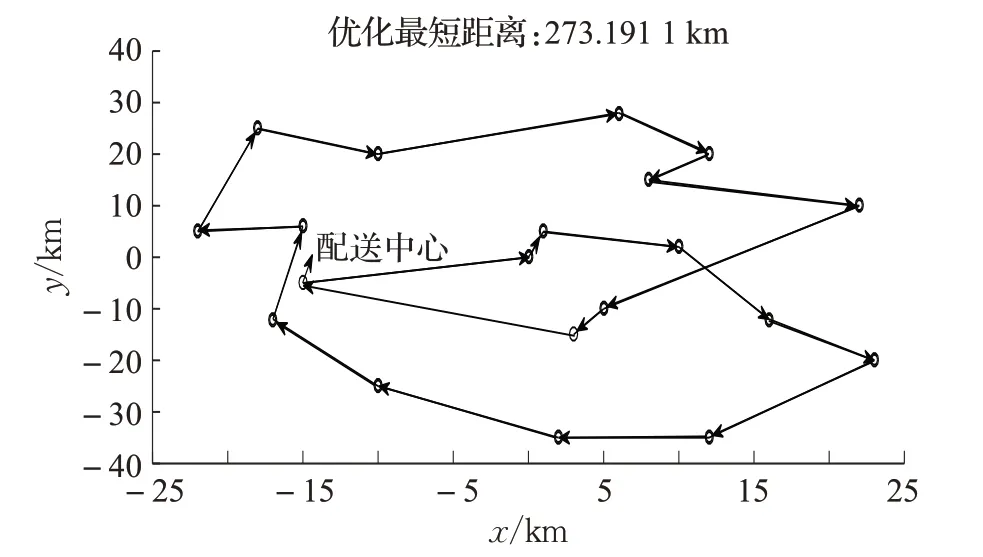
圖9 20個服務點的車輛路徑最優化距離

通過表7的計算結果可知，經過使用CPIIWD算法的優化計算后，20 個需求服務點上，使用4 輛運輸車輛的最小運輸總成本為1 765.836元，這與文獻[38]中使用的基本智能水滴算法求解計算的最小運輸總成本2 168.9元、最短運輸距離353.804 km相比，每條運輸路徑的拓撲結構不同，路徑距離分別減少20 km 左右，這說明使用精準搜索的鴿群算法改進水滴算法，求解VRPMOMTW問題的結果更為精確，優化效果更為明顯。

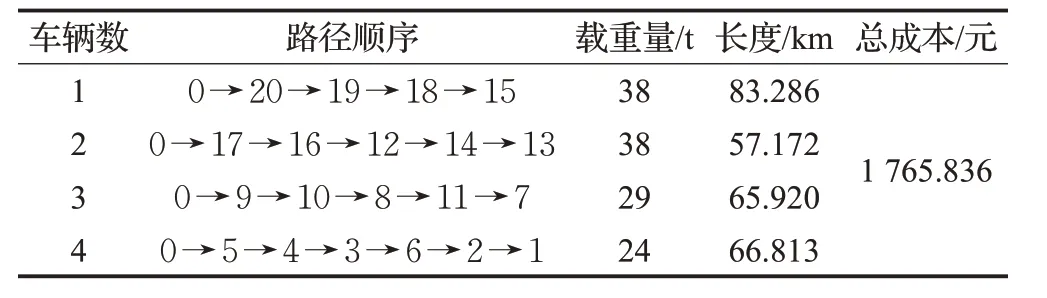
表7 不同配送路徑上車輛的載重量

根據圖8 的收斂計算結果可知，為了增強CPIIWD算法求解VRPMOMTW問題的可信性，通過該算法800次迭代后，求解計算的最小運輸成本達到最優，且該算法經過260 次的計算后，求解結果基本達到平穩狀態，說明該算法能夠快速收斂到問題的最優解。

由圖9 的計算結果可知，使用CPIIWD 算法求解VRPMOMTW 中的路徑距離后，車輛從配送中心出發后，經過20個需求服務點形成不同運輸路徑拓撲結構，最終返回配送中心，且計算獲得的車輛路徑最優化距離為273.191 1 km，這與文獻[33]中使用基本智能水滴算法求解的車輛路徑距離減少80 km左右，降低了車輛運輸總成本。

5 結語

（1）針對帶時間窗車輛路徑組合規劃目標的差異化問題，提出多目標多時間窗車輛路徑規劃模型，實現了物流車輛運輸成本、運輸距離和配置數量的抽象建模，拓展了物流車輛路徑規劃問題的研究范圍。

（2）針對基本智能水滴算法求解車輛路徑規劃模型速度慢、結果精度低等問題，利用地圖羅盤算子和地標算子分別改進了水滴的流動速度和方向，同時，利用自適應變鄰域擾動策略干擾水滴攜帶的泥土量，提高水滴算法的搜索計算速度和求解精度。

（3）針對多目標模型的求解難度大、處理過程復雜等問題，采用理想點法和多目標優化與罰函數混合方法，分別處理多目標函數與復雜約束條件間的關系，簡化了人工智能算法求解模型處理能力。

（4）通過利用經典標準測試函數與物流車輛路徑規劃問題作為仿真實例，測試了鴿群-水滴算法的優化性能以及驗證了模型求解的可行性，并從尋優次數、收斂計算時間和平均值等指標考核了4 種不同算法的計算結果，證明了CPIIWD 算法求解車輛路徑問題的優越性，雖然改進的智能水滴算法在車輛路徑規劃問題中獲得較好的求解結果，但該算法能否在不同工程優化問題中表現出良好性能，這需要進一步對本文算法的深入應用展開研究。