求解BBM方程的一個新的高精度線性化差分算法
沙嬋娟, 張 虹
(1.山西大學數學科學學院, 太原 030006; 2.西南交通大學希望學院, 成都 610400)
本文考慮如下帶有非線性擴散項和耗散項的Benjamin-Bona-Mahony(BBM)方程的初邊值問題:
ut-uxxt+ux-uxx+uux=0,(x,t)∈
(xL,xR)×(0,T]
(1)
u(x,0)=u0(x),x∈[xL,xR]
(2)
u(xL,t)=u(xR,t)=0,t∈[0,T]
(3)
其中u0(x)是已知光滑的函數.方程(1)是Benjamin等[1]在研究非線性彌散系統中長波的單向傳播時為考慮非線性波在傳播中的耗散原理而提出的,是對描述淺水波損耗現象的KdV方程的修改.對這類問題的研究有重要的理論和應用價值.
文獻[2-4]研究了方程(1)解的存在唯一性及收斂性.文獻[5-12]對BBM方程進行了數值方法研究,但一般都只具有二階理論精度.文獻[13,14]對問題(1)-(3)分別提出理論精度為O(τ2+h4)的兩層非線性差分格式和三層線性差分格式,但非線性差分格式數值求解時需要非線性迭代,耗時較多.本文先對方程(1)進行線性化離散處理,僅需在時間層將非線性項uux部分外推到n-1層即可保證時間層具有二階理論精度.然后,利用Richardson外推[13]的思想在空間層進行外推,本文使空間層具有四階理論精度,從而對問題(1)-(3)構造一個新的三層線性差分格式.在不能得到其差分解的最大模估計的情況下,本文綜合運用數學歸納法和離散泛函分析方法[15],直接證明了該格式的收斂性和穩定性.數值算例表明,相對于文獻[14]的三層線性格式,該格式的精度有了大幅度的提高.
2 差分格式及其可解性

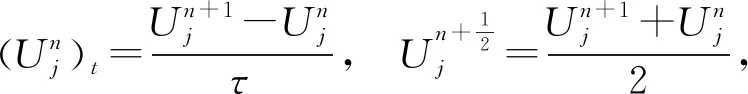
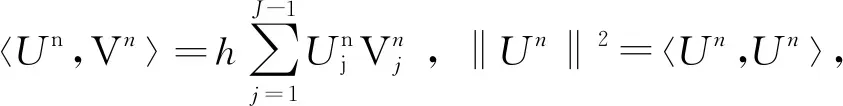
對問題(1)~(3)考慮如下有限差分格式:
(j=1,2,…,J-1;n=1,2,…,N-1)
(4)
(5)
(6)
(7)
引理2.1[15]對n=0,1,2,…,N,恒有
定理2.2若時間步長τ充分小,則差分格式(4)~(7)是唯一可解的.
證明 用數學歸納法.顯然,U0和U1是由(5)式和(6)式唯一確定的.假設U0,U1,…,Un-1,Un(n≤N-1)是唯一可解的.現在我們來考慮(4)式中的Un+1,則有
(8)
將(8)式與Un+1作內積,由邊界條件和分部求和公式[16]有
(9)
由引理2.1有
(10)
又
(11)
將(10)和(11)式代入(9)式,并利用引理2.1,整理有
于是,只要取τ足夠小,使得當1-Cτ>0時,方程組(8)僅有零解.因而,差分格式(4)~(7)中的Un+1是唯一可解的.
3 差分格式的收斂性與穩定性
差分格式(4)~(7)的截斷誤差定義如下:
(12)
(13)
(14)
(15)
由Taylor展開可知,當h,τ→0時,
(16)
引理3.1[13]設u0∈H2.則初邊值問題(1)~(3)的解滿足
‖u‖L2≤C, ‖ux‖L2≤C, ‖u‖L∞≤C.

證明 數學歸納法.記
由(12)~(15)式減去(4)~(7)式得
Qj(j=1,2,…,J-1;n=1,2,…,N-1)
(17)
(18)
j=1,2,…,J-1
(19)
(20)
其中
由引理3.1以及(16)式知,存在與τ和h無關的常數Cu和Cr使得
Cr(τ2+h4)n=1,2,…,N-1
(21)
再由初始條件(5)以及(18)式可得以下估計式:
‖e0‖=0,‖U0‖∞≤Cu
(22)
現假設

l=1,2,…,n(n≤N-1)
(23)
其中Cl(l=1,2,…,n)為與τ和h無關的常數.則由離散Sobolev不等式[16]和Cauchy-Schwarz不等式有
(24)
‖Ul‖∞≤‖ul‖∞+‖el‖∞≤
(25)
(26)
整理得
(27)
由引理3.2以及微分中值定理有
即
(28)
同理
(29)
再取τ和h充分小,使得
(30)
則由引理2.1、引理3.2以及(28)~(30)式有
‖en+1‖2+‖en‖2)
(31)
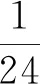
‖en+1‖2+‖en‖2)
(32)
(33)
將(31)~(33)式代入(27)式整理有
τ‖rn‖2+2(Cu+1)(‖en+1‖2+
(34)
將(34)式從1到n遞推,由引理3.1得
(35)
又
T·(Cr)2(τ2+h4)2
(36)
將(23)、(36)式代入(35)式,利用離散Gronwall不等式[16],取時間步長τ充分小以滿足
于是有
(Cn+1)2(τ2+h4)2,n=1,2,…,N-1,

最后,由離散Sobolev不等式有
‖en‖∞≤O(τ2+h4),n=1,2,…,N.
定理3.3設u0∈H2.若時間步長τ和空間步長h充分小,則差分格式(4)~(7)的解滿足

證明 對于充分小的τ和h,由定理3.2有
注定理3.3表明差分格式(4)~(7)的解Un以‖·‖∞關于初值無條件穩定.
4 數值算例
當t=0時,由于耗散還沒有產生,所以在數值實驗中,我們把問題(1)~(3)中的初值函數取為RLW方程的初值函數[14](t=0時)
由于不知道方程(1)的精確解,我們用類似文獻[13-14]中的處理方法將細網格 (τ=h=1/160)上的數值解作為精確解來估計誤差.固定xL=-20,xR=40,T=10.就τ和h的不同取值,對本文的格式(記為格式1)和文獻[14]的線性格式(記為格式2)進行了比較,在幾個不同時刻的誤差及其對理論精度的檢驗見表1、2. 其中

Order=log2Rn.

表1 兩個格式在不同時刻的l∞誤差比較

表2 對格式1的理論精度O(τ2+h4)的數值檢驗
從數值算例可以看出,本文的格式是可行的.由于格式1在數值計算時的已知層(第n-1層)很少,所以誤差傳遞累積也較少,從而格式1比格式2具有更高的精度.

