無限維空間上的波方程和Schr?dinger 方程解的存在性和唯一性

梁冬冬

(四川大學數學學院， 成都 610064)

1 引 言

設H為無限維可分的復Hilbert空間，u為定義在H上的泛函.類似于有限維空間上的偏微分方程，我們也可以建立一個以u為未知函數的H上的偏微分方程.我們稱這樣的微分方程為無限維空間上的偏微分方程. 這一類微分方程來源于量子場論、晶體的固態理論及具有無限多個自由度的系統、無限維隨機控制理論等[1-8].

在有限維空間中，我們可以利用概率論的方法研究偏微分方程，推廣這種方法也可以去研究無限維空間的偏微分方程. 比如：文獻[2-3] 利用隨機微分方程得到了無窮維空間中的線性拋物偏微分方程的解，即Feynman-Kac 表示. 文獻[4]利用正、倒向隨機微分方程將線性Feynman-Kac 公式推廣到了非線性拋物方程的情形. 文獻[5]推廣了這種方法，并利用非耦合的正、倒向隨機方程得到了無窮維空間的半線性拋物方程的初值問題的mild解，進而利用動態規劃方法研究了對應的隨機最優控制問題.

另一方面，有界開集上的無限維空間中的拋物偏微分方程的初邊值問題也引起了部分學者的關注.例如文獻 [6] 利用停時對正向隨機微分方程的解過程做了反射，得到了有界開集上的無窮維空間上的線性拋物偏微分方程的齊次邊值問題解的存在唯一性.然而，非齊次方程的邊值問題還未解決.當前，無限維空間中的微分方程的研究多局限在研究空間中的拋物方程.利用這種方法獲得的較好的結果見文獻[7]，該文解決了耦合的正倒向隨機方程的適定性問題，并利用正、倒向隨機微分方程的解來表示無窮維的HJB 方程. 但是，用這種方法，解的表示公式越來越復雜，因而可以求解的偏微分方程的類型受到了極大的限制，比如本文中的無限維空間的波方程和Schr?dinger 方程就無法求解. 由于無限維橢圓方程的L2理論不完善，本文利用Guassian-Sobolev 空間，結合關于橢圓方程的假設條件，使用半群方法得到了無限維空間中的波方程和Schr?dinger 方程解的存在性、唯一性.

2 預備知識

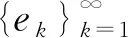
(1)

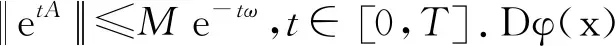
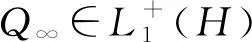
以L2(H,μ)表示H上在測度μ下平方可積的函數全體，?φ,ψ∈L2(H,μ)，在L2(H,μ)中定義內積

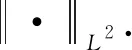
定理 2.1[8]對任意x,y∈D(A),Q∞是唯一的使得下列等式成立的算子.?x,y∈D(A*)，

〈Q∞x,A*y〉+〈Q∞A*x,y〉=-〈Qx,y〉.

令EA(H)=span{e〈h,x〉;h∈D(A*)}.由測度的 Fourier 變換可得EA(H)在L2(H,μ)中稠密.

定義2.2任意k∈N，定義映射

Dk:EA(H)?L2(H,μ)→L2(H,μ)，φ→Dkφ，

以L2(H,μ;H)表示H上所有的H-值的在測度μ下平方可積的映射全體. ?φ,ψ∈L2(H,μ;H), 以如下方式定義內積：

則L2(H,μ;H)在以上內積下是一個Hilbert 空間.

定義2.3以如下方式定義算子

D:EA(H)?L2(H,μ)→L2(H,μ;H)，

引理 2.4[8]任意φ,ψ∈EA(H),?k∈N,有下列等式成立：

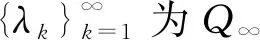
引理 2.5[8]任意k∈N，Dk和D為可閉算子.

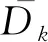
定義2.6?φ，ψ∈Dom(D)，定義內積如下：

則Dom(D)在這個內積下是一個Hilbert 空間，稱為Sobolev 空間，記為W1,2(H).

以L2(H,μ;L2(H))表示H上的在μ測度下平方可積的L2(H)-值映射全體，L2(H)表示H上所有的Hilbert-Schmidt 算子全體.?φ,ψ∈L2(H,μ;L2(H))，在L2(H,μ;L2(H))中以如下方式定義內積：

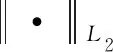
定義2.7按如下方式定義映射D2,

D2:EA(H)?L2(H,μ)→L2(H,μ;L2(H))，

φ→D2φ，

其中D2φ為φ的二階導數，作用為：?α,β∈H，

αk，βh分別表示α，β在H的基下的坐標.

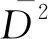
〈φ,ψ〉W2,2=〈φ,ψ〉W1,2+〈D2φ,D2ψ〉L2(H,μ;L2(H))，

則Dom(D2)∩Dom(D)在這個內積下為一個Hilbert 空間，記為W2,2(H). 注意到空間W2,2(H)中的函數的二階導數關于測度μ在幾乎處處的意義下只是一個Hilbert-Schmidt 算子.

定義2.8定義算子DQ如下：

DQ:EA(H)?L2(H,μ)→L2(H,μ;H)，

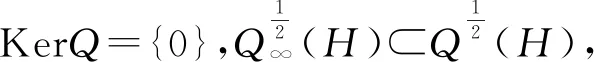
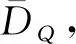
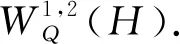
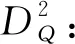
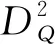
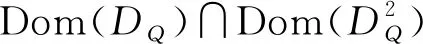
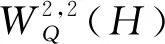
?x∈H

(2)

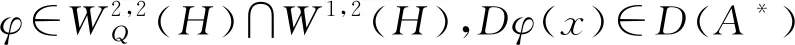
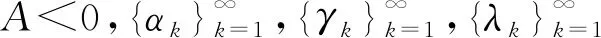
?φ,ψ∈EA(H)，以如下方式定義內積：

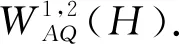
定義2.12按照如下方式定義一個算子

φ→Lφ，

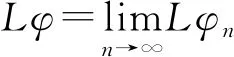
引理 2.13[8]對任意φ，ψ∈EA(H)，以下等式成立：

?φ∈EA(H)，不妨設φ(x)=e〈h,x〉，h∈D(A)，

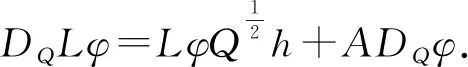
兩次利用引理2.13 的(ii)容易得到

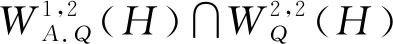
定義2.14在空間EA(H)中按照如下方式定義范數.?ψ∈EA(H)，

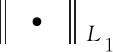
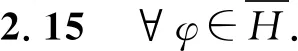
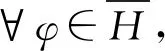
因而

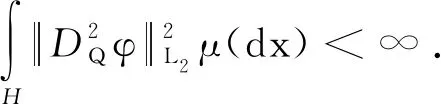
〈x,ADφ(x)〉)|μ(dx)≤

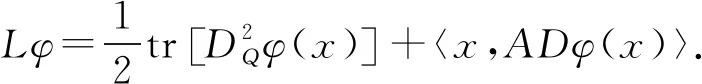
3 橢圓方程弱解的存在唯一性

考慮如下方程，?g∈L2(H,μ)， ?x∈H，

(3)

利用算子L將方程(3)形式地寫成

Lφ=g

(4)

注意到方程(3)和(4)本質上不是同一個方程.算子L的作用方式一般不是方程(3)的左邊項的形式.然而它們的解之間確實有著很強的關系.

若φ∈S滿足方程(4)，在(4)式兩邊乘以ψ后在H上積分得

左邊項利用引理2.13式(ii)知?ψ∈S，

(5)

反之，若存在φ∈S滿足式(5)，由引理 2.13(ii)得

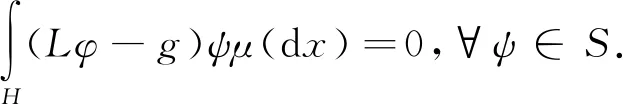
由S在空間L2(H,μ)中的稠密性得(4).

定義3.1設g∈L2(H,μ).φ∈S稱為方程(4)的解，若任意ψ∈S，φ滿足積分恒等式(5).

在無窮維空間中，橢圓方程的解很難直接得到，主要原因在于無窮維空間上橢圓的能量估計一般不成立.而且，在何時成立著能量估計也尚不清楚. 本文在橢圓方程的解的基礎之上去研究波方程和Schr?dinger方程.

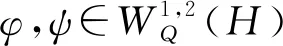
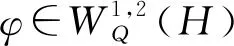
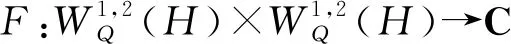
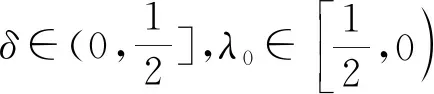
證明 由范數和雙線性函數F的定義，容易得到結論.

定理3.5對任意g∈L2(H,μ)，λ∈C， Reλ≥λ0，方程(4)有唯一弱解.

證明 根據命題3.4，利用Lax-Milgram定理易

得定理3.5的結論.

當方程(4)的弱解正則性足夠高時，弱解就是定義3.1中的解了. 然而遺憾的是，無論是(4)的解還是弱解，都不是方程，g∈L2(H,μ)，

(6)

的解，即幾乎處處的x∈H滿足方程(6).

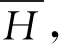
證明 由命題2.15易得.

4 波方程弱解的存在唯一性

接下來，我們考慮如下形式的波方程，

(7)

應用前文所定義的算子L，我們將方程(7)形式上寫成下列方程：

(8)

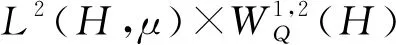
u=(u1,u2)T，φ=(φ1,φ2)T.

定義算子G如下：

u→Gu，

其中

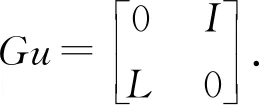
進一步，利用算子G將方程(8)寫成下式：

在M中重新定義內積如下：?u1,u2∈M，設u1=(u11,u12)T，u2=(u21,u22)T，則

〈u1,u2〉=〈u11,u21〉L2+〈u12,u22〉L2+

假設4.1令λ∈C.方程λω-Lω=f的弱解ω滿足：

(i)f∈L2(H)時，ω∈S；

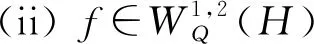
(i)f∈S時，ω∈D((L)2).

注意到當H是一個有限維空間時，假設4.1就是橢圓方程弱解的正則性，成立；當算子Q和A均是有限秩算子，且二者的值域空間相同時，由偏微分方程弱解的正則性易知假設4.1也成立.

引理4.2若假設4.1中成立，則對任意F=(f1,f2)T∈M，λ∈C，Reλ2≥λ0，|λ|>1，方程(λI-G)U=F有唯一解U∈S，且解U滿足估計式.

證明 ?F=(f1,f2)T∈M，令U=(u1,u2)T.方程(λI-G)U=F等價于

設方程λ2I-Lωi=fi的弱解為ωi.則ωi∈S，i=1,2. 令u1=λω1+ω2，u2=λω2+Lω1.則U=(u1,u2)T為方程(λI-G)U=F的解. 事實上，我們有

λu1-u2=λ2ω1+λω2-λω2-Lω1=

λ2ω1-Lω1=f1，

λu2-Lu1=λ2ω2+λω1-λω1-Lω2=

λ2ω2-Lω2=f2.

因此，?λ∈C，Reλ2≥λ，λI-G為滿射.

對任意F=(f1,f2)T∈S×S，λ∈C，|λ|>1，方程(λI-G)U=F的解U=(u1,u2)T∈S×S.為計算方便，將L2(H,μ)和L2(H,μ;H)中的內積簡記為〈·,·〉則

〈f1,f2〉-〈Lf1,f1〉+〈f2,f2〉=

〈f1-Lf1,f1〉+〈f2,f2〉=

〈λu1-u2-λLu1+Lu2,λu1-u2〉+

〈λu2-Lu1,λu2-Lu1〉≥

|λ|2〈u1,u1〉-2Reλ〈u1,u2〉+

(1+|λ|2)〈u2,u2〉-

|λ|2〈Lu1,u1〉+〈Lu1,Lu1〉-〈Lu2,u2〉≥

|λ|2〈u1,u1〉-2|λ|〈u1,u2〉+

〈Lu1,Lu1〉-〈Lu2,u2〉≥

(|λ|2-|λ|)〈u1,u1〉+

(1+|λ|2-|λ|)〈u2,u2〉+

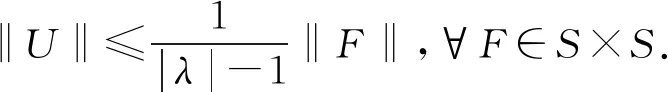
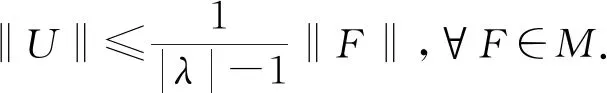
定理 4.3當假設4.1成立時，算子G能生成M上的一個C0半群{T(t)}t≥0，滿足‖T(t)‖≤et，?t≥0.

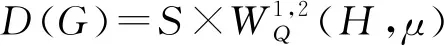
所以G能生成C0半群{T(t)}t≥0.證畢.

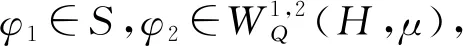
證明 設T(t)是G所生成的C0半群.令

(u1,u2)T=T(t)(φ1,φ2)T，

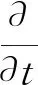
則u1為(8)的解.

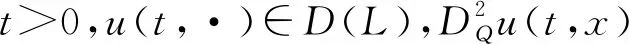
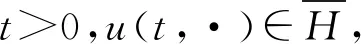
考慮方程

(9)

利用算子L將方程(9)形式上寫為下列方程：

(10)

定理5.1當假設4.1中的 (i) 成立時，iL能生成L2(H,μ)上的一個C0半群.

證明 因EA(H)?Dom(L)=Dom(iL)，則S在L2(H,μ)中稠密，這里Dom(iL)表示iL的定義域.由引理 2.13(ii)，得ReL2=0.?φ∈S，且?λ∈C，Reλ≥λ0時，λI-L為滿射.所以存在λ1∈C，使得λ1I-iL為滿射，從而L是極大耗散的，算子iL能生成L2(H,μ)上的一個C0半群.

推論5.2在定理5.1 的條件下，方程(10)存在唯一解u∈C1([0,∞),S).