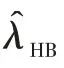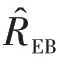基于無失效數據的某型發動機可靠性參數Bayes估計
李東兵,胡文林
(1.海軍參謀部某訓練中心,北京100841;2.92728部隊,上海200436)
在定時截尾試驗中,對于高可靠性、高精度的產品,經常會出現極少失效甚至是無失效數據的情形[1-4]。如何在無失效數據情況下對產品的可靠性參數進行科學合理的評估,具有重要的理論和實用價值[5-10]。
文獻[11]給出了泊松分布參數的期望Bayes(Expected Bayes,E-Bayes)表達式;文獻[12]給出了只有一個失效數據時失效概率的E-Bayes估計;文獻[13]在特定超參數先驗分布的條件下,推導了失效率的EBayes 估計;文獻[14]采用修正多層Bayes 方法對某型軸承的失效概率進行估計;文獻[15]研究了復雜系統可靠度的多層Bayes估計。
這些文獻雖然對可靠性參數作出了較為準確和穩健的估計,但大多只專注于某一類估計方法。
本文在某型裝備發動機無失效數據服從指數分布時,探討失效率的多層Bayes估計方法和E-Bayes估計方法,對比2種方法的推導證明過程,并結合實例數據分析得到可靠度的估計結果,指出E-Bayes 估計方法的結果更為準確和穩健,且計算更加方便。
1 失效率的多層Bayes估計
本文研究對象為某型裝備發動機,已知其儲存失效數據服從指數分布,其概率密度函數為:
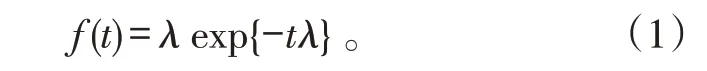
式(1)中:t>0;0<λ<∞,λ 為指數分布失效率。
1.1 多層先驗分布的確定
在指數分布下,失效率對應的共軛先驗分布為Gamma分布[16],其密度函數為:
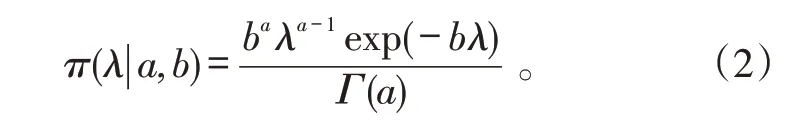
根據超參數的減函數構造法[17],對密度函數關于λ 求一階導:
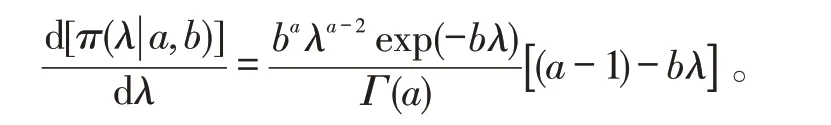
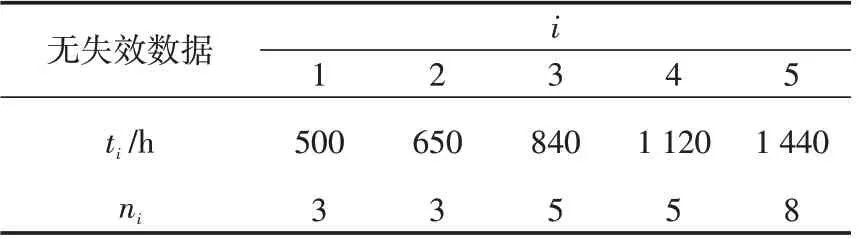
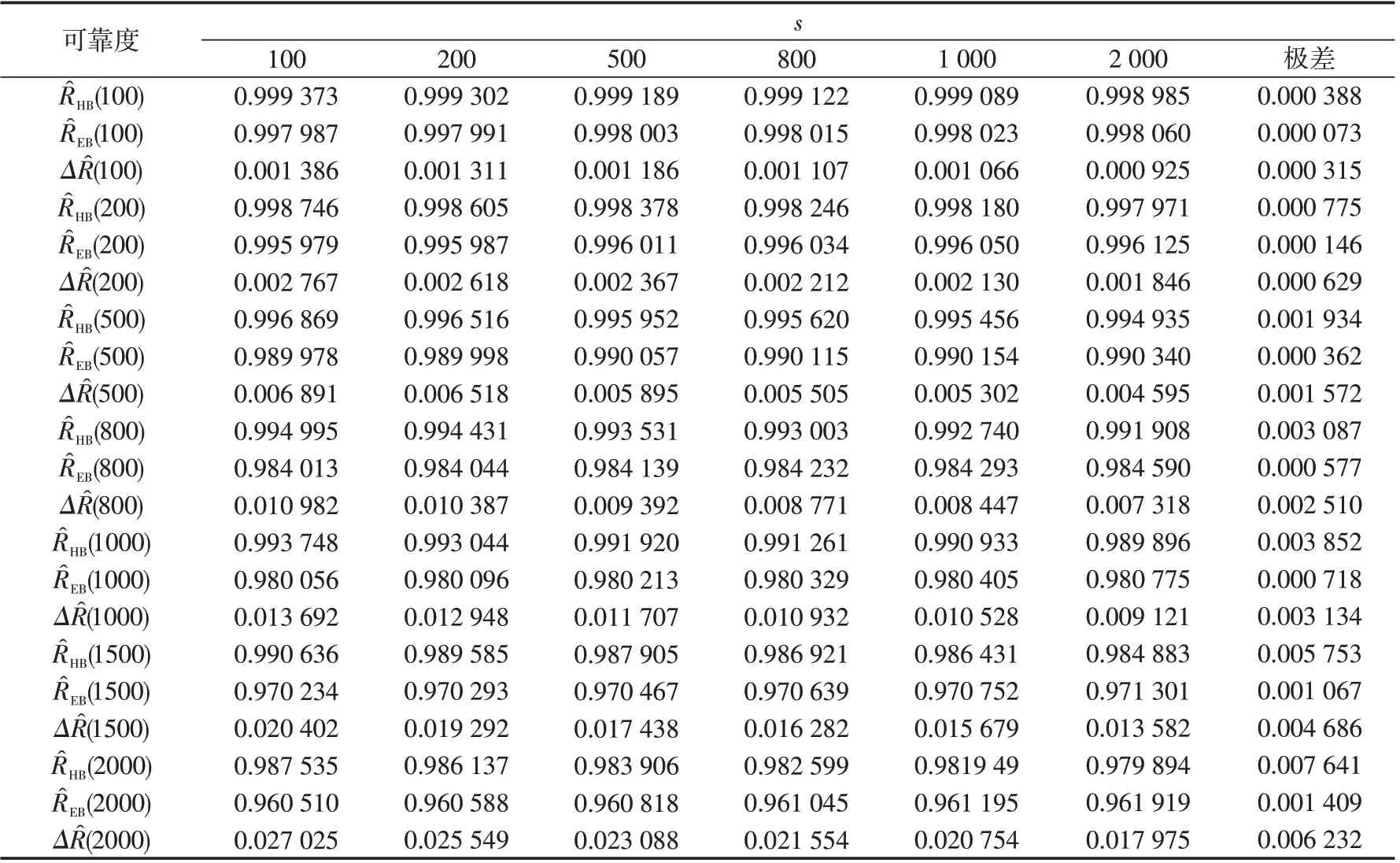
因而,當0 考慮a 和b 分別服從[0,1]和[0,s]上的均勻分布,則失效率λ 的多層先驗密度函數為: 對壽命服從指數分布的產品進行m 次定時截尾試驗,結果為{ }(ni,ri,ti),i=1,2,…,m 。其中:ti為在第i 次試驗中的截尾時間,且t1 假設失效率λ 的多層先驗密度函數πHB(λ)可由式(3)給出,則在平方損失下,λ 的多層Bayes估計為: 證明: 1)似然函數。設隨機變量Xi表示第i 次定時截尾試驗中發生失效的樣品個數,則Xi~π(nitiλ),即Xi服從參數為nitiλ 的泊松分布: 式中:ri=0,1,2,…,ni,i=1,2,…,m。 事實上,X1,X2,…,Xm是相互獨立的,則失效率λ的似然函數表示為: 試驗結果為無失效情形時,ri=0,i=1,2,…,m,由此得到無失效情形下失效率λ 的似然函數為: 2)后驗分布。依據Bayes 定理,λ 的多層后驗密度為: 記(b+Q)λ=ξ ,由于b>0,Q>0,0<λ<∞,故0<ξ<∞。代入式(5)右端的分母積分項可得: 代入式(5)可得 3)多層Bayes 估計。在平方損失下,失效率λ 的多層Bayes估計為: 令(b+Q)λ=ξ,同式(5)的推導過程,可得: 證畢。 在式(1)、(2)的基礎上,與1.1節相同,對b 設立一個上界s,s>0 為某一常數,確定超參數的取值范圍為0 根據1.3 節的無失效數據的描述,假設失效率λ的先驗密度函數π(λ|a,b)由式(2)給出,則在平方損失下,λ 的E-Bayes估計為: 證明: 1)似然函數。與1.3 節證明相同,似然函數為L(0|λ)=exp(-Qλ)。 2)后驗分布。若λ 的先驗密度函數由式(2)給出,則依據Bayes定理,λ 的后驗密度為: 記(b+Q)λ=ξ,同式(5)的推導過程,可得: 3)λ 的Bayes估計。在平方損失下,λ 的Bayes估計為: 4)λ 的E-Bayes 估計。在平方損失下,失效率λ的E-Bayes估計為: 證畢。 產品壽命服從指數分布,則其可靠度函數為: R(t)=exp(-λt)。 由1.3節和2.3節分別給出的λ 的多層Bayes估計和E-Bayes估計,得出可靠度R(t)的多層Bayes估計和E-Bayes估計如下: 穩健性是統計學中的一個專門術語,20世紀70年代開始在控制理論的研究中流行起來,用以表征控制系統對特性或參數擾動的不敏感性[18]。本文主要以可靠性參數估計值的極差來表征由2種估計方法得到的估計值的穩健性,極差值越小,反映得到的可靠性參數估計值越穩健。 表1 發動機無失效數據Tab.1 Zero-failure data of the engine 表2 λ 的2類估計結果Tab.2 Calculation results of different estimations on λ ×10-5 表3 R(t)的2類估計結果Tab.3 Calculation results of different estimations on R(t) 圖1 s=1 000 時可靠度的2類估計值Fig.1 Calculation results of two types of estimations while s=1 000 圖2 可靠度2類估計值的極差Fig.2 Ranges of two types of estimations on R(t) (3)在推導和計算過程中,相比于含有二重積分的多層Bayes估計,失效率的E-Bayes估計計算更為方便簡潔,因而也更適用于工程應用中。 下一步將針對壽命服從其他分布情形時的參數估計值進行討論,并探討超參數服從的分布類型對估計值的影響。1.2 多層先驗密度函數的確定
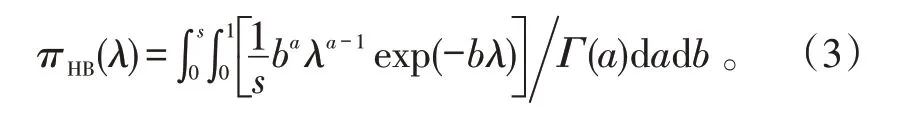
1.3 失效率的多層Bayes估計

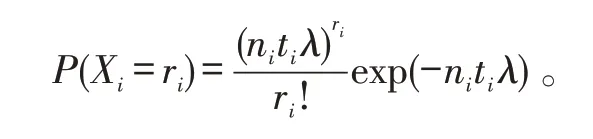

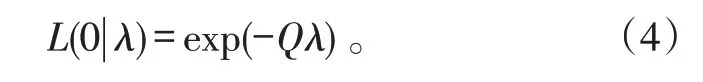
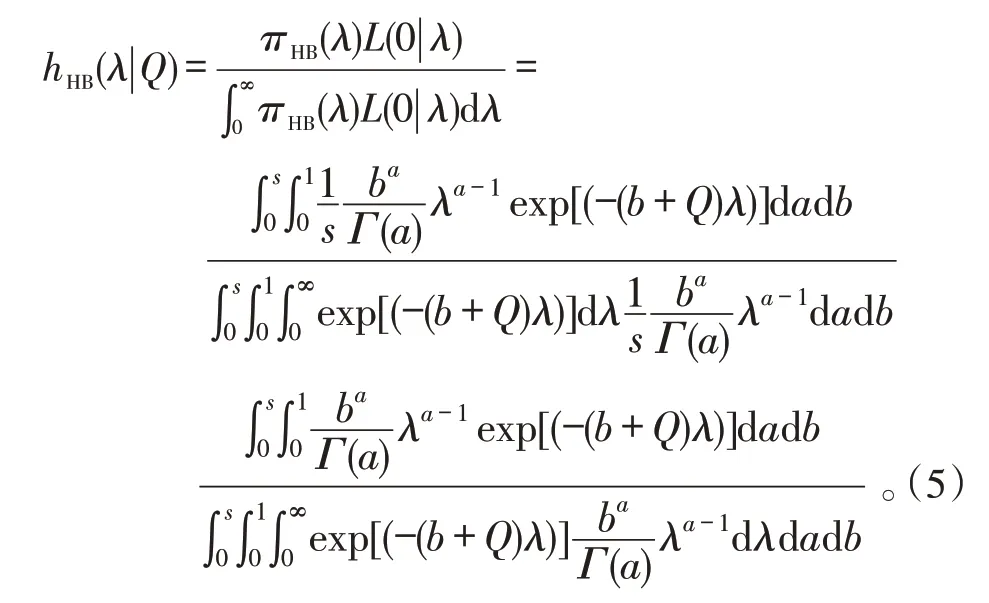
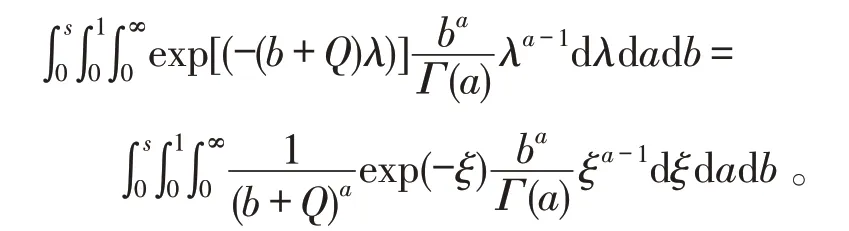
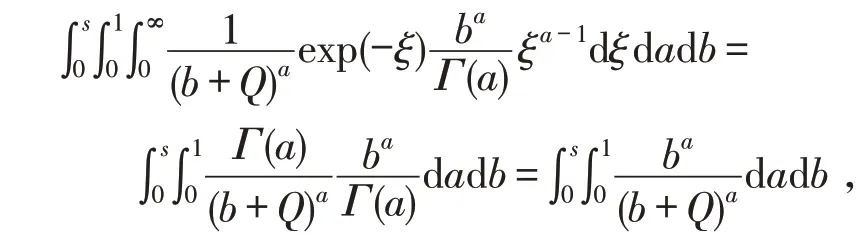
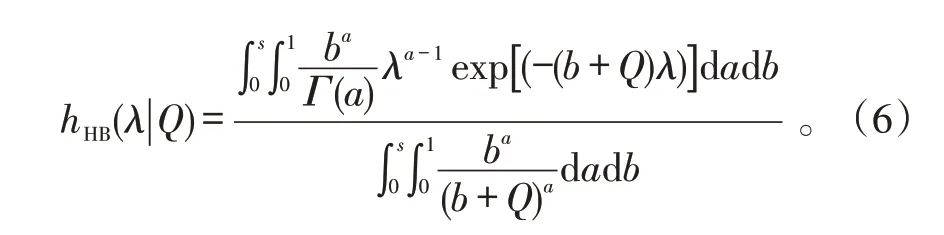
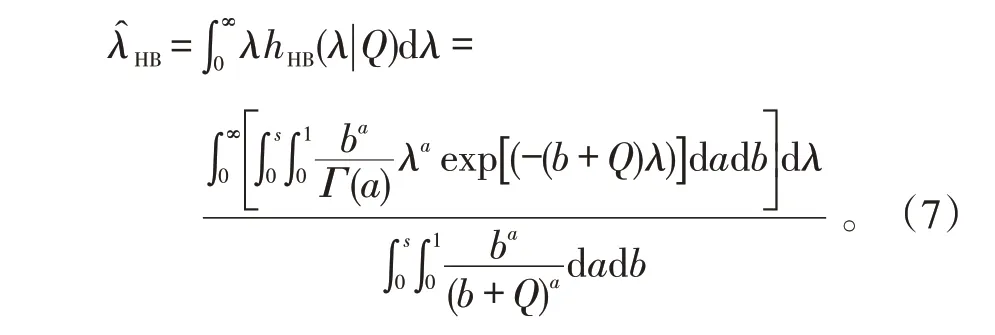

2 失效率的E-Bayes估計
2.1 先驗分布的確定
2.2 失效率的E-Bayes定義

2.3 失效率的E-Bayes估計

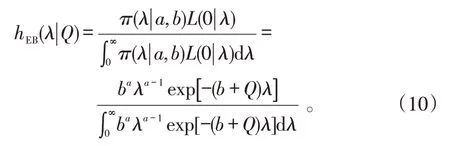
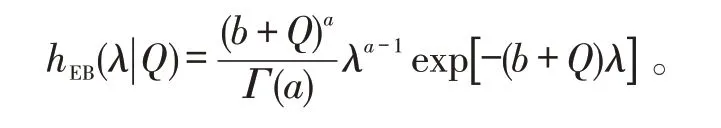


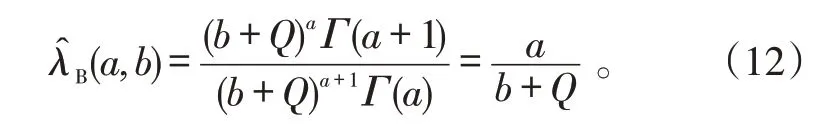
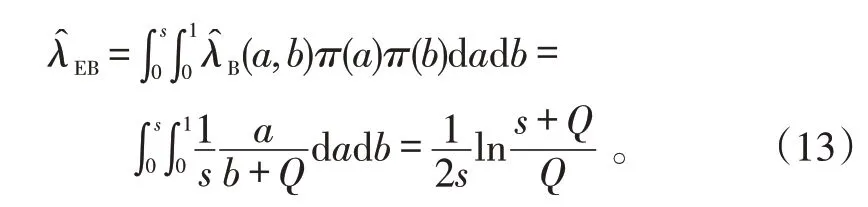
3 實例分析
3.1 可靠度的估計

3.2 參數估計的評價
3.3 可靠性參數估計及分析



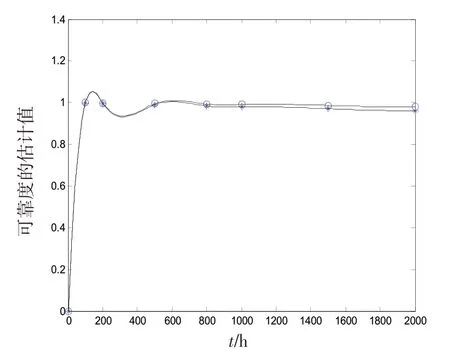
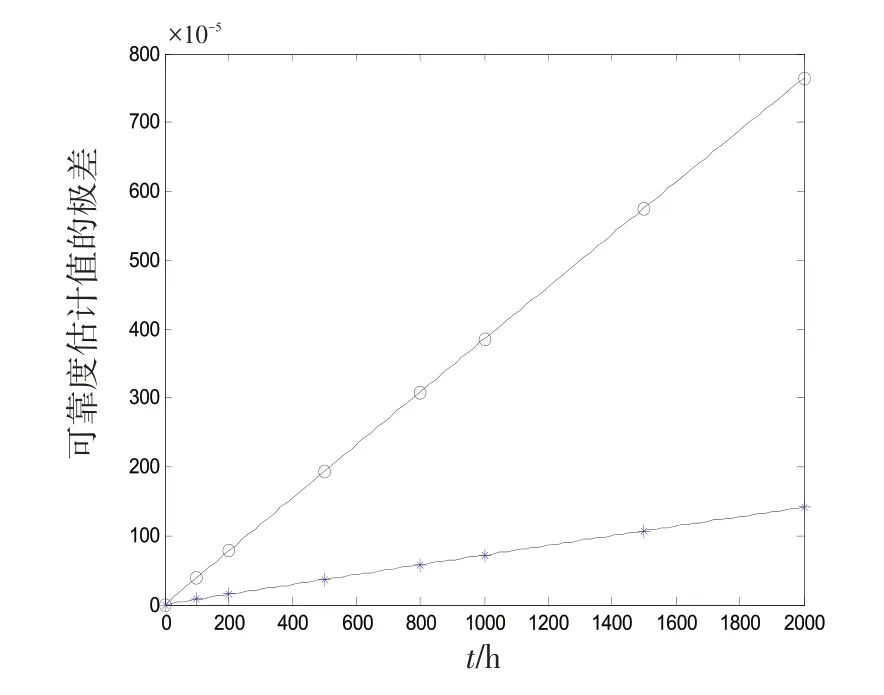
4 結論