Theoretical predictions of lattice parameters and mechanical properties of CL-20 under the temperature and pressure
-, -, -, g, -, -, AN o-n, -
(1.College of Science, East China University of Technology, Nanchang 330013, China;2.Institute of Fluid Physics, Chinese Academy of Engineering Physics, Mianyang 621900, China;3. College of Nuclear Science and Engineering, East China University of Technology, Nanchang 330013, China;4. College of Physics, Sichuan University, Chengdu 610064, China)
Abstract: The molecular dynamics with condensed-phase optimized molecular potentials for atomistic simulation studies (COMPASS) force field have been employed to study high energetic material CL-20. The lattice parameters and elastic constants in the pressure range of 0~10 GPa (for ε-CL-20) and 0~20 GPa (for α-, β-, and -CL-20) at room temperature, and in the temperature range of 100~500 K at room pressure are predicted. The good agreement of lattice parameters, pressure-volume relation and elastic constants of the greatest stability phase ε-CL-20 shows the accuracy of our simulations. The theoretical predictions of lattice parameters and mechanical properties of CL-20 under temperature and pressure may provide powerful guidelines for the engineering application and await further experimental confirmation.
Keywords: Molecular dynamics; Energetic materials; Lattice parameter; Elastic constants
1 Introduction
2,4,6,8,10,12-hexanitro -2,4,6,8,10,12-hexaazaisowurtzitane (CL-20) has the largest density in the current existing energetic materials, and it is superior to conventional high-energy propellants and explosives[1-2]. Thus, CL-20 is considered as the most potential and powerful high energy density materials. Its synthesis has been a breakthrough in the synthesis of high explosive investigations. CL-20 is a caged nitramine explosive with the formula C6H6N12O12, as shown in Fig. 1. The structure of CL-20 molecule consists of two five-member rings and a six-member ring. There exhibits four different crystal structures of CL-20, three pure crystallization phases, β,, and ε, and a hydrate phaseαat ambient conditions, as shown in Fig.2.
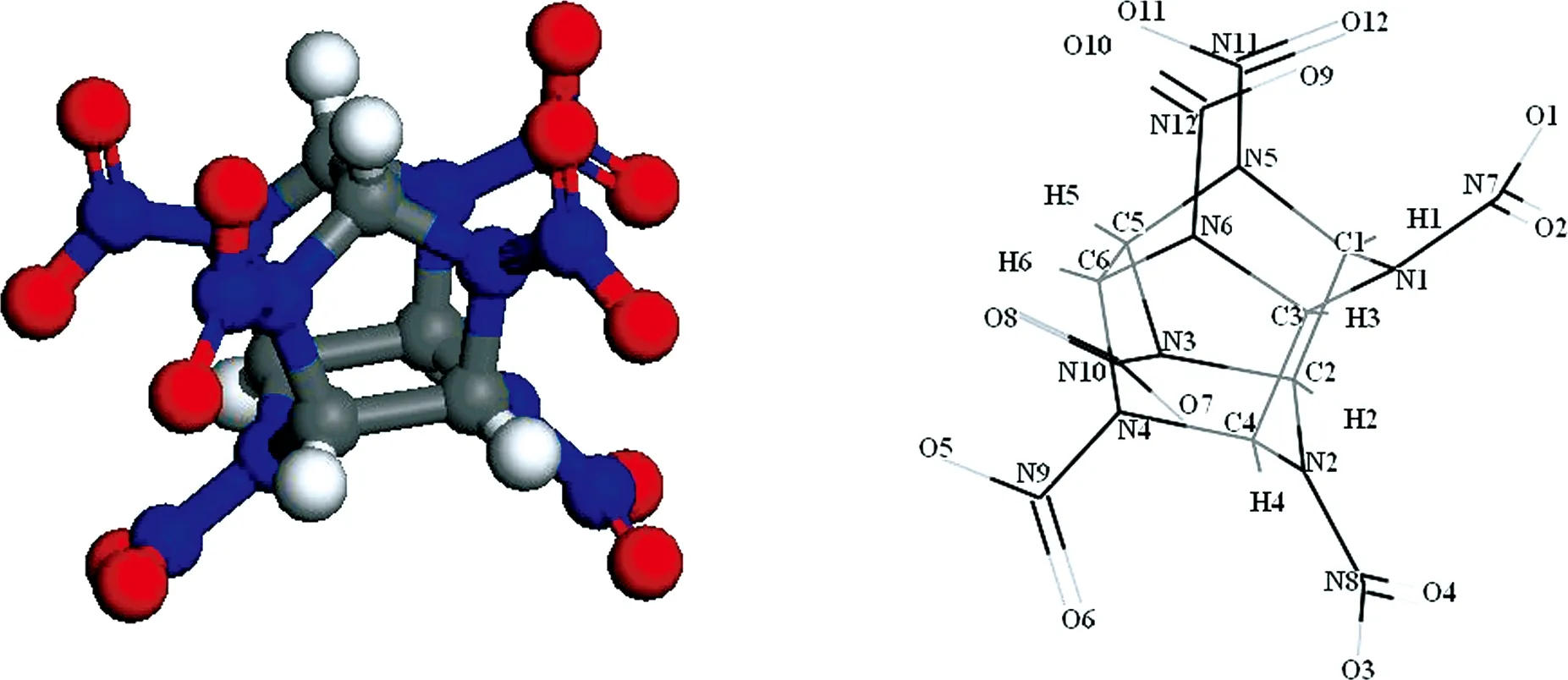
Fig.1 Conformation and atomic numbering of C6H6N12O12 molecule in CL-20

Fig.2 Unit cell of CL-20: (a) ε- CL-20, (b) - CL-20, (c) β- CL-20 and (d) α- CL-20
At ambient conditions, the stabilities of these polymorphs are known to be ε>>α>β.ε-CL-20 has the largest density and best thermochemical stability among them, which makes it the popular phase for applications and investigation. Up to now, several experimental[3-4]and theoretical[5-7]studies have been reported for ε-CL-20. In experimental studies, Pinkerton has reported the pressure-volume relationship of this polymorph up to 2.5 GPa firstly[3]. Later, Gump and Peiris have measured the isothermal compression data of ε-CL-20 up to 5.6 GPa both at ambient temperature and 75 ℃[4]. The ambient-temperature isothermal bulk modulus of 13.6 GPa with a pressure derivative of 11.7 has also been reported according to the third-order Birch-Murnaghan equation of state (EOS)[4]. In theoretical studies, some efforts have been done to investigate the EOS of CL-20 through density functional theory (DFT)[5-6], Molecular dynamics (MD) simulation[7], and molecular packing (MP) method[7], respectively. Based on DFT, using GGA-PW91 method, the ultrasoft pseudopotentials (USP) with 396 and 545 eV planewave basis set have been employed to calculate the EOS of ε-CL-20, respectively[5]. Compared with the 396 eV predictions, the 545 eV predictions show larger deviations from the experiment, especially in the low range of pressure. It should be noted that the agreement of 396 eV results origin from the insufficiency of energy cutoff for the plane-wave basis set. Subsequently, Sorescu and Rice calculated the lattice parameters of CL-20 under pressure using DFT method with a plane-wave basis set of within the pseudopotential approximation[6]. The calculated pressure-volume relationship of CL-20 also has large deviations from the corresponding experimental data, as the similarity as of 545 eV results[6]. The large deviations in both the lattice parameters and EOS for energetic materials CL-20 are mainly due to a lacking reproduce of van der Waals (vdW) forces in current DFT. In addition, both of the MD within the rigid-molecule approximation and MP methods are employed to calculate the pressure-volume relation of CL-20[7]. The calculated zero pressure lattice parameters are accurate, but the deviations have been getting larger with increasing pressure for comparison with the experimental results. These results indicate that both of the two methods can not predict the accurate lattice parameters under high pressure[7]. The condensed-phase optimized molecular potentials for atomistic simulation studies (COMPASS) force field could give the well description of the intermolecular interaction potential. As this theory could effectively improve the accuracy of the simulations for energetic materials, it has been employed for simulating the energetic materials, such as HMX[8]and RDX[9]. In this paper, we also employ the MD simulations with COMPASS force field to investigate the lattice dynamics of CL-20.
At present, CL-20 has not been fielded in military and civil applications yet because of its high sensitivity.Some efforts have been done to reduce the mechanical sensitivities of CL-20 based polymer bonded explosives such that the hazardous energetic material may be handled and even machined into desired shapes[10-13]. Whatever, it is fundamental and significant to know the mechanical properties of pure CL-20 from atomic and molecular scale. As is well known, the elastic constant is a key parameter to investigate the mechanism properties. Though the experimental approaches of elastic constants, such as Brillouin scattering, ultrasonic velocity measurements, and resonant ultrasound spectroscopy, are mature technology, it is still difficult to measure the elastic constants of energetic materials accurately. For example, HMX(C22,C33,C55,C66,C23)[14-16]and RDX(C11,C22,C44,C12)[17-19], the experimental data differ from each other and some deviations are very large. This is because that the samples of energetic materials are not perfect enough with some crystallographic defects. In literature, only one experimental study on the elastic constants of ε-CL-20 has been reported by Haycraft using Brillouin scattering spectroscopy at ambient conditions[20]. The theoretical investigation on the elastic properties of the other phase (α-, β-, and-CL-20) are lacking in literature, especially in high pressure and temperature range.
The goal of this work is to predict the lattice parameters and mechanical properties under high temperature and pressure of four CL-20 crystal phases (α-, β-,-, and ε-CL-20). This work is respected to give a comparative and complementary theoretical support for experiments.
2 Computational details
2.1 Molecular dynamics calculations
The MD simulations with COMPASS[21]force field are employed for four polymorphs (α-, β-,-, and ε-CL-20). The initial lattice parameters and internal atomic coordinates are taken from experimental data. ε- and-CL-20 belong to the monoclinic symmetry, while α- and β-CL-20 belong to the orthorhombic symmetry. The conformation and atomic numbering of C6H6N12O12molecule are shown in Fig. 1, together with the unit cell of four pure polymorphs, which are plotted in Fig. 2. The molecular dynamics simulations are performed with the Discover code. A computational supercell size of 2×2×2 unit cells are done. The MD simulations are carried out in the isothermal-isobaric NPT ensemble with the Andersen thermostat method[22]and Berendsen barostat method[23]to control the system pressures and temperatures respectively. The long-range non-bond Coulombic and vdW interactions are managed using the Ewald simulation method[24].The calculated system is relaxed for 1×105time steps with the time step of 1 fs in the equilibration run at each target of temperature and pressure.
2.2 Elastic constants
The elastic stiffness tensorcijklcan be expressed as
(1)
whereεklis the strain,cijklis the elastic constant (matrix) andσijis the stress. There are thirteen independent components of the elastic stiffness tensor for monoclinic crystal, and nine independent components for orthorhombic crystal.
For monoclinic phase[25]
BV=(1/9)[C11+C22+C33+2(C12+C13+
C23)]
(2)
GV=(1/15)[C11+C22+C33+3(C44+C55+
C66)]-(C12+C13+C23),
(3)
BR=h[a(C11+C22-2C12)+b(2C12-2C11-
C23)+c(C15-2C25)+c(C15-2C25)+
d(2C12+2C23-C13-2C22)+2e(C25-
C15)+f]-1
(4)
GR=15{4[a(C11+C22+C12)+b(C11-C12-
C23)+c(C15+C25)+d(C22-C12-C23-
C13)+e(C15-C25)+f]/h+3[g/h+
(5)
b=C23C55-C25C35
c=C13C35-C15C33
d=C13C55-C15C35
e=C13C25-C15C23
C15C25)+C15(C12C25-C15C22)+
C25(C23C35-C25C33)
2C12C13C23
h=2[C15C25(C33C12-C13C23)+
C15C35(C22C13-C12C23)+
C25C35(C11C23-C12C13)]-
For orthorhombic phase[26]
BV=(1/9)[C11+C12+C33+2(C12+C13+
C23)
(6)
GV=(1/15)[C11+C22+C33+3(C44+C55+
C66)-(C12+C13+C23)
(7)
BR=Δ[C11(C22+C33-2C23)+C22(C33-
2C13)-2C33C12]+C12(2C23-C12)+
C13(2C12-C13)+C23(2C13-C23)]-1
(8)
GR=15{4[C11(C22+C33+C23)+C22(C33+
C13)+C33C12}-C12(2C23+C12)-
C13(2C12+C13)-C23(C13+C23)]/Δ+
3[(1/C44)+(1/C55)+(1/C66)]}-1
(9)
Δ=C13(C12C23-C13C22)+C23(C12C13-
The arithmetic average of the Voigt and Reuss bounds is named the Voigt-Reuss-Hill (VRH) average and employed to estimate the elastic moduli of polycrystals[27-29]:
BV+BR=2BH,GV+GR=2GH
(10)
Young’s modulusEcan be calculated by
E=9BG/(3B+G)
(11)
Possion’s ratioνare obtained by the following formula
ν=(3B-2G)/[2(3B+G)]
(12)
3 Results and discussion
3.1 Lattice parameters
The calculated lattice constants and unit cell volume at ambient conditions from our NPT-MD optimizations are shown in Tab. 1, together with the available experimental[30-31]and other theoretical data[6-7]. With regard to experiments, the deviation of our calculated unit cell volume are -0.46% (ε-CL-20), -3.48% (-CL-20), 2.02% (α-CL-20), and -1.61% (β-CL-20). Our calculated results agree with the experimental and theoretical results.
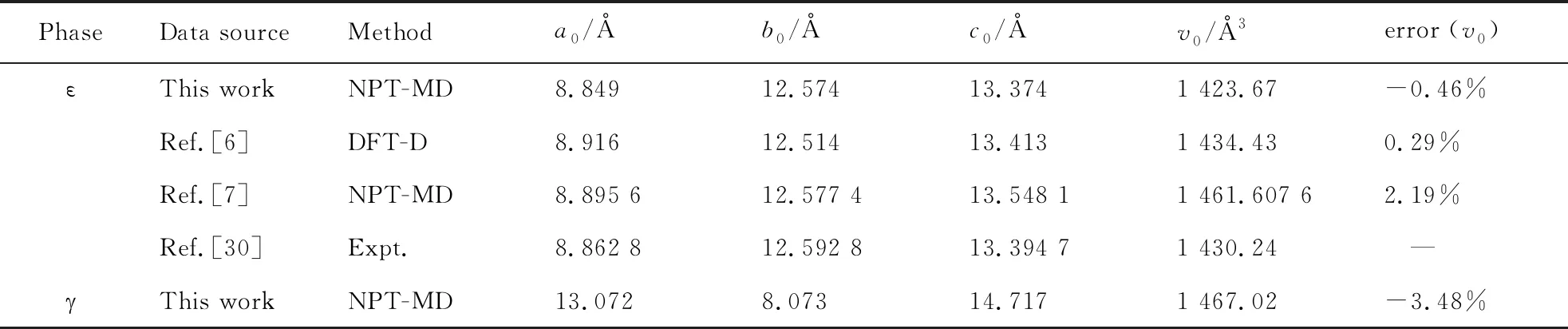
Tab.1 Calculated equilibrium lattice parameters at ambient conditions in comparison to the theoretical and experimental values
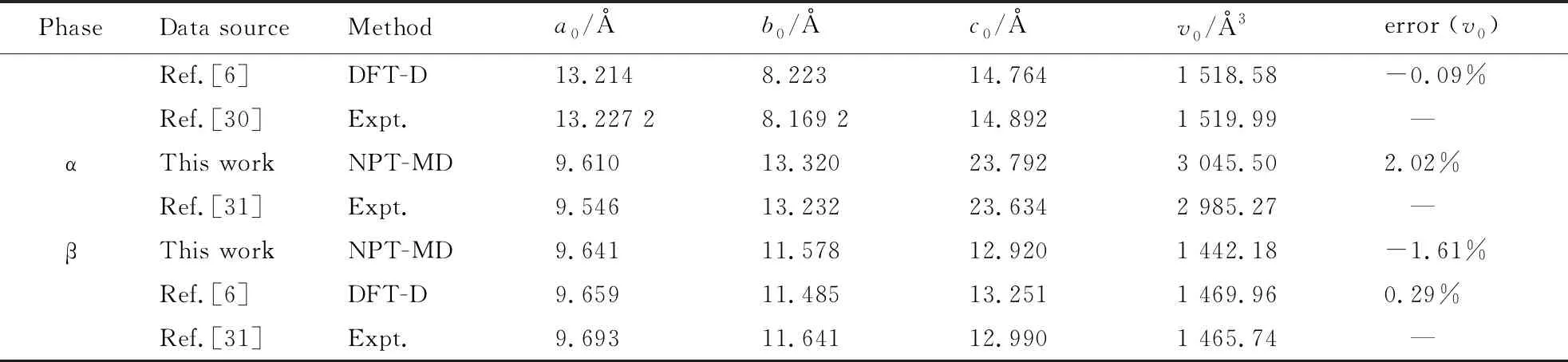
(Tab.1 Continued)
3.2 Equation of state
The EOS is important for mitigation of hazardous materials like CL-20 in preparation, transportation, storage, and handing process. We plot the variation of lattice parameters under pressure or temperature in Fig.3.

Fig.3 Variation of cell volume and lattice constants of ε-CL-20 (a~d), -CL-20 (e~h), α-CL-20 (i~l), β-CL-20 (m~p) with pressure at 298 K, or with temperature at room pressure
As shown in Fig. 3(a), for the ε-CL-20, the zero pressure theoretical crystal volume with DFT method overshoot the experimental results[3-4]and then the discrepancy gets smaller with increasing pressure. Due to the poor description of vdW force, which plays an important role in CL-20 molecular crystal, the DFT calculation overestimates the cell volume[7]. While the dispersion-corrected simulations using a semi-empirical correction term proportional added to Kohn-Sham energy functional improve the accuracy[7]. The zero pressure theoretical crystal volumes from the MP and NPT-MD method agree well with the experimental results, while the discrepancy increases with increasing pressure. These results suggest that the intermolecular potential used in the MP and NPT-MD methods can not predict lattice parameters accurately under high pressure[14]. Our calculated results of NPT-MD method with CMPASS force field agree well with experimental data[3-4]. Similarly, our theoretical predictions of lattice parameters consist well with the experiments in the temperature range of 100 to 298 K[30]. Though the experimental data for comparison is insufficient, our theoretical predictions of lattice parameters should be accurate in the higher pressure or temperature range. In addition, we predict the lattice parameters of α-CL-20, β-CL-20, and-CL-20 in the pressure range of 0 to 20 GPa or in the temperature range of 100 to 500 K, as is shown in Fig. 3(e) ~ 3(p).
There are several different formulations of EOS. Here, we fit theP-Vdata of CL-20 to Murnaghan EOS[32]and Birch-Murnaghan EOS[33]respectively. The third-order Birch-Murnaghan EOS can be written as follows,
(13)
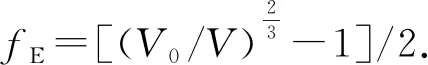
(14)
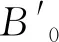
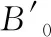
Tab. 2 The calculated bulk modulus B0 and its first pressure derivative of CL-20 compared with experimental and theoretical values
3.3 Elastic and mechanical properties
Though the experimental approaches of elastic constants, such as Brillouin scattering, ultrasonic velocity measurements, and resonant ultrasound spectroscopy (RUS), are mature technology, it is still difficult to measure the elastic constants of energetic materials accurately. Several experimental efforts have been done on the conventional explosives, RDX and HMX. The experimental data differ from each other and some deviations are large, such as HMX (C22, C33, C55, C66, C23)[14-16]and RDX (C11, C22, C44, C12)[17-19]. Due to the poor description of vdW force, which plays an important role in CL-20 molecular crystal, the DFT calculation can not predict the elastic constants of CL-20 accurately. The good predictions of lattice parameters and EOS above indicate that the molecular dynamics simulations with COMPASS force field can give accurate description of interatomic binding forces and intermolecular interaction in CL-20 crystal. The elastic constants of four polymorphs at ambient conditions (α-, β-,-CL-20, and ε-CL-20) are listed in Tab.3. The good agreement of experimental and theoretical elastic constants for ε-CL-20 proves the validity and accuracy of the calculation for CL-20. The elastic modulus of CL-20 under temperature at room pressure or under pressure at 298 K are calculated and listed in Tab. 4. The temperature and pressure are the influencing factors in preparation, transportation, storage, and handing process. The predicted elasticity under temperature and pressure can provide powerful guidelines for the engineering application and further experimental investigations.
We plot the variation of bulk modulusB, shear modulusG, Young’s modulusE, and Possion’s ratioνas a function of the pressure as shown in Fig. 4. The mechanical moduli of α-, β-,-, and ε-CL-20 are found to increase with increasing pressure. On account of the greatest stability of ε phase among the four polymorphs, we also calculate the temperature dependence of bulk modulusB, shear modulusG, Young’s modulusE, and Possion’s ratioνfor ε-CL-20, as listed in Tab.5. Though there are no experimental mechanical moduli at different temperature for comparison, the good agreement of bulk modulusBHand shear modulusGHat ambient conditions
shows the accuracy of our simulations[20]. The mechanical moduli under temperature can be fitted to a third order polynomial,i.e.,
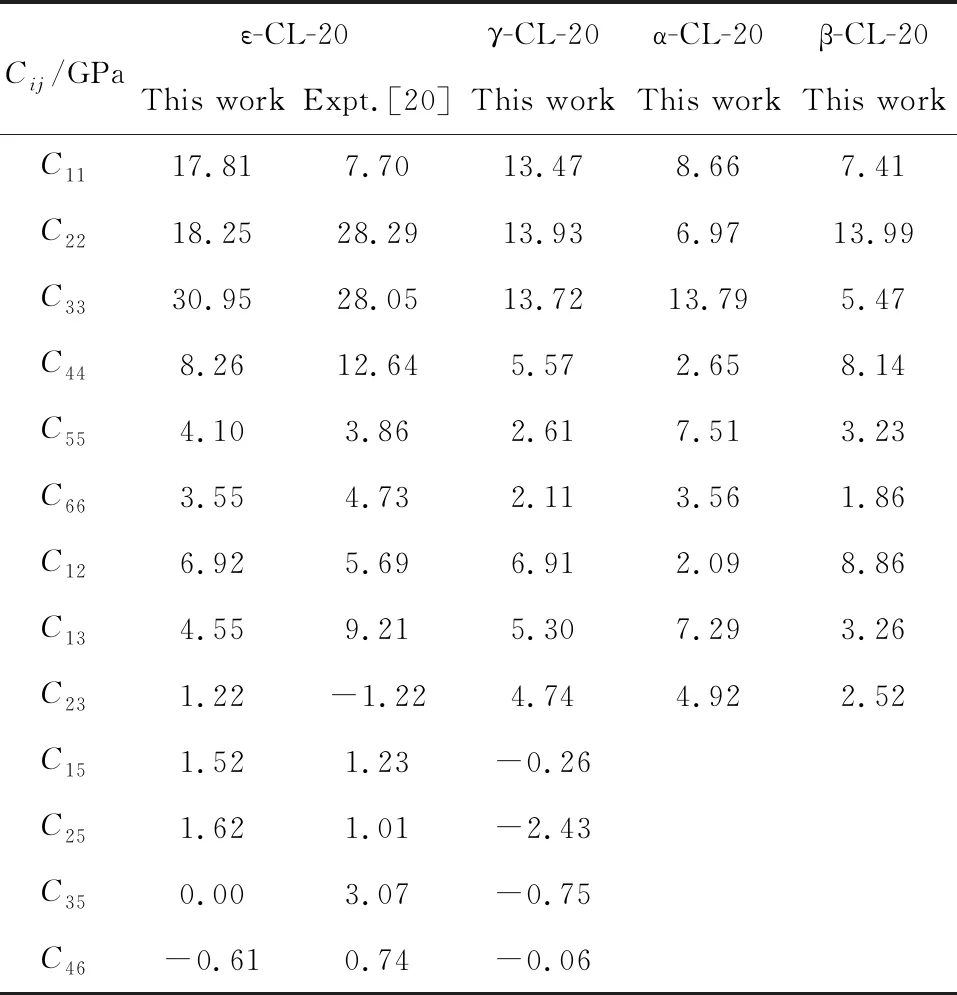
Tab.3 The calculated Cij of CL-20 at ambient conditions and the experimental data for ε-CL-20
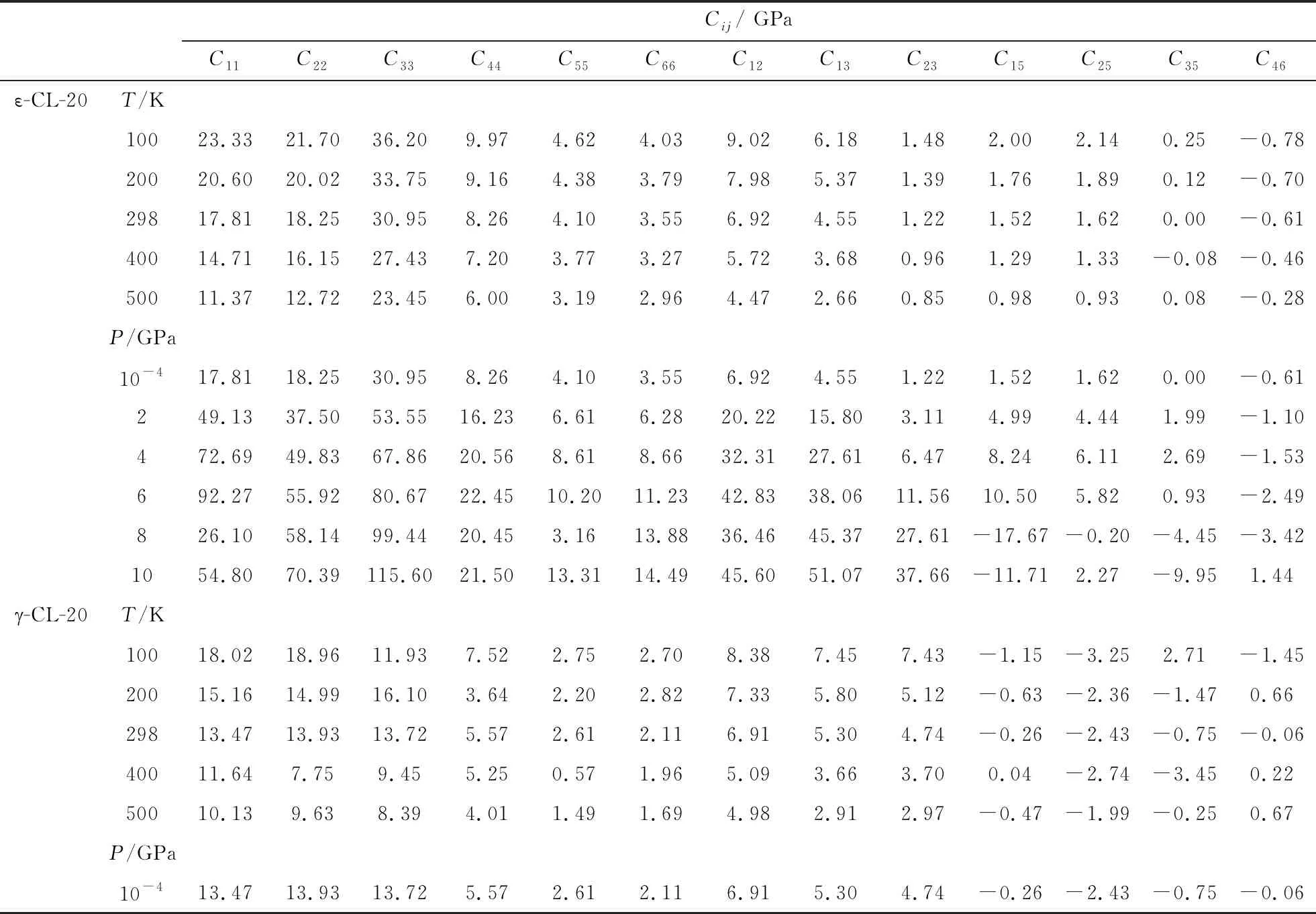
Tab.4 The calculated elastic modulus Cij of CL-20 under temperature at room pressure or under pressure at 298 K
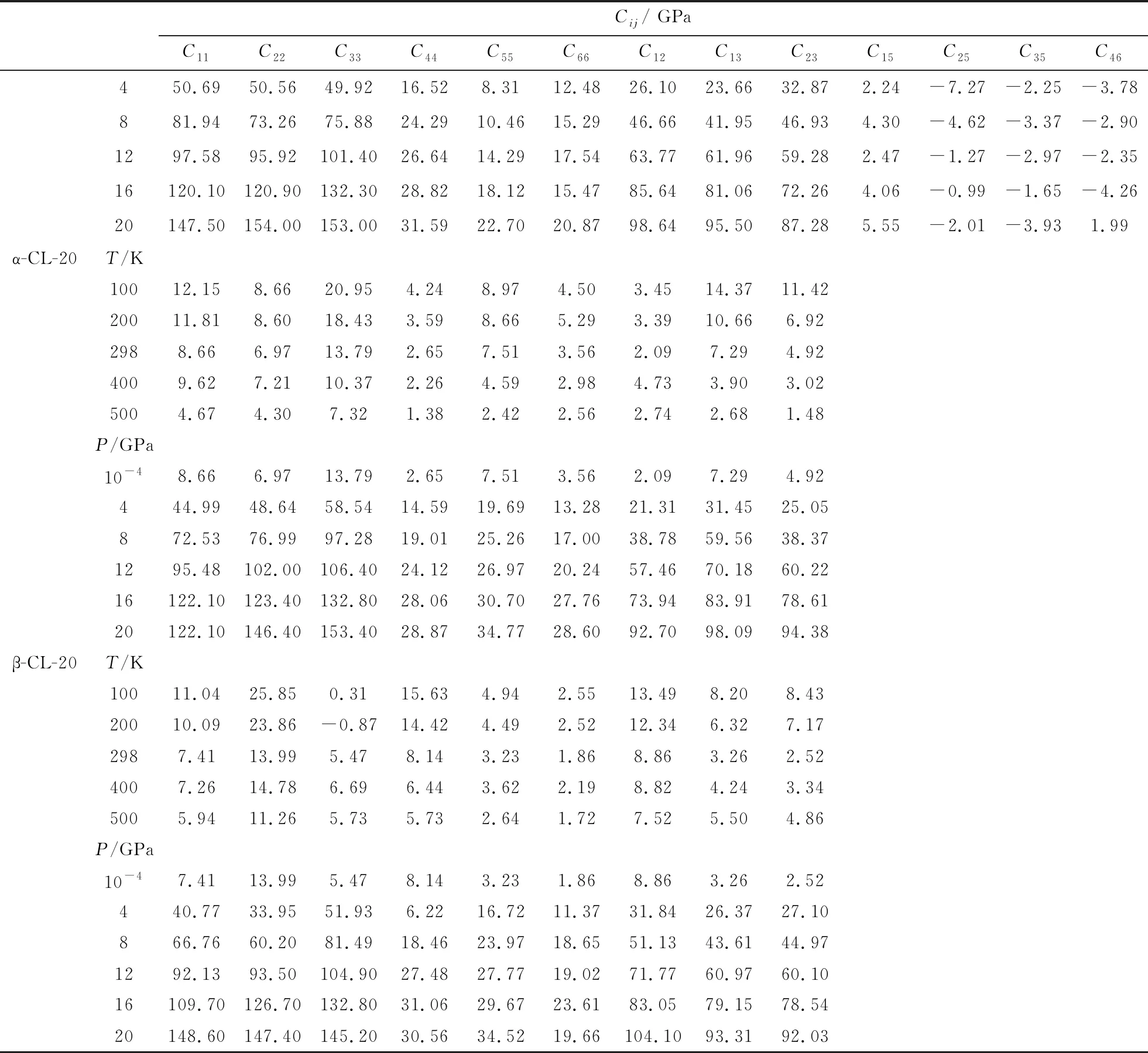
(Tab.4 Continued)
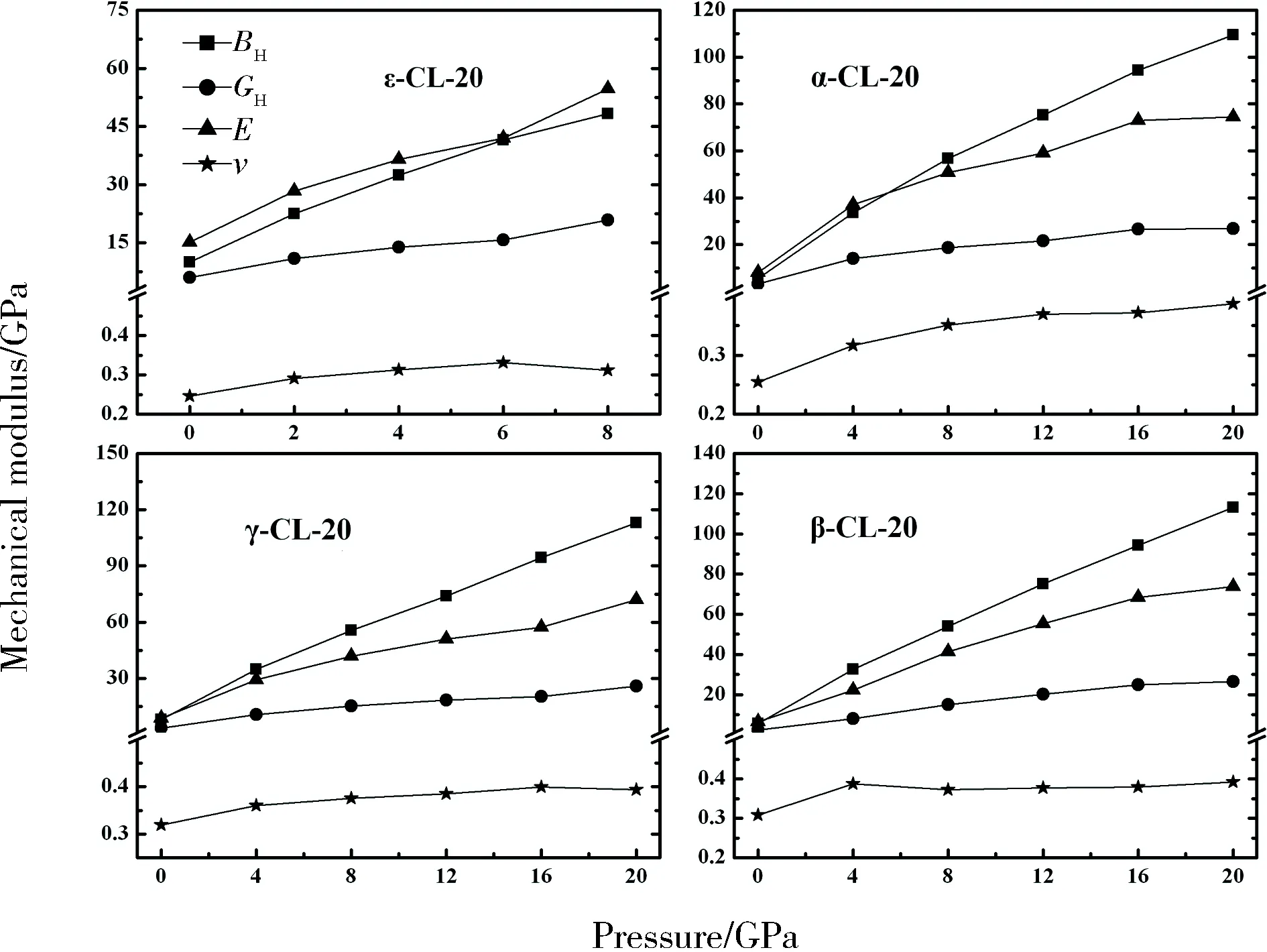
Fig.4 The calculated pressure dependence of bulk modulus BH (squares), shear modulus GH(circles), Young’s modulus E(triangles), and Possion’s ratio ν (stars) for CL-20
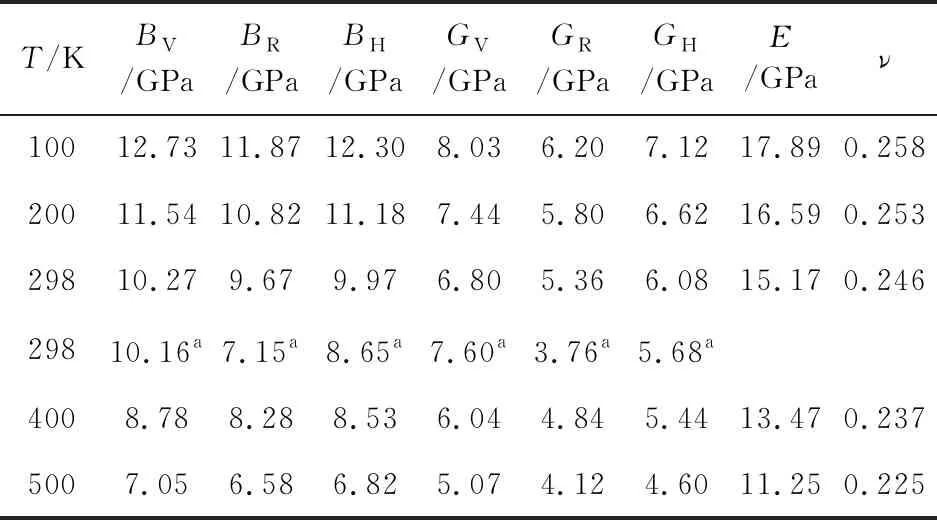
Tab.5 The calculated temperature dependence of bulk modulus B, shear modulus G, Young’s modulus E, and Possion’s ratio ν for ε-CL-20
aThe data in Ref. [20] is calculated on the basis of the ambient experimental elastic constants by the Voigt-Reuss-Hill approximation.
BH(T)=13.411-0.011T+3.823×
10-6T2-1.502×10-8T3
(15)
GH(T)=7.682-0.006T+6.633×
10-6T2-1.338×10-8T3
(16)
E(T)=19.320-0.015T+1.539×
10-5T2-3.344×10-8T3
(17)
ν(T)=0.262-3.463×10-5T-3.632×
10-8T2-8.412×10-11T3
(18)
4 Conclusions
Molecular dynamics simulations have been employed to study the lattice parameters, EOS, elastic constants, and mechanical modulus under pressure and temperature. The good agreement between molecular dynamics results and experimental data prove that the molecular dynamics simulations with COMPASS force field can give good description of interatomic binding forces and intermolecular interaction in CL-20 crystal. From the above investigations, we have the following conclusions:
(1) The calculated equilibrium lattice parameters of four polymorphs (α-, β-,-, and ε-CL-20) at ambient conditions are in good agreement with the experiments. We predict the lattice parameters of CL-20 under pressure and temperature. The bulk modulusB0and its pressure derivativeB0′are obtained by fitting the pressure-volume points to Birch-Murnaghan EOS and Murnaghan EOS respectively.
(2) The elastic constants of four polymorphs (α-, β-,-, and ε-CL-20) under pressure and temperature are predicted. Our molecular dynamics simulated results of elastic constants ofε-CL-20 at ambient conditions present good agreement with the experimental data. The predicted elastic constants of four polymorphs under pressure and temperature should be accurate and provide powerful guidelines for further experimental measurements. In terms of the Voigt-Reuss-Hill approximation, the mechanical modulus are obtained.

