BP神經網絡算法預測多組分材料中子屏蔽效果方法研究

林海鵬，李國棟，陳法國，韓 毅，梁潤成

(中國輻射防護研究院,太原 030006)

屏蔽設計中優化是一個重要問題，在實現屏蔽效果的同時應盡可能降低材料重量、體積、造價等必要考慮的目標。遺傳算法等現代優化方法已廣泛應用于輻射屏蔽設計優化[1]，圍繞算法模型、種類和策略等的原理研究也較為豐富；遺傳算法進行屏蔽設計優化的一個瓶頸問題在于：需要進行屏蔽計算的次數太多，通常等于種群數量與迭代次數的乘積；而屏蔽計算往往耗時較長，尤其采用蒙特卡羅之類的概率論模擬方法，較多粒子數和復雜模型下過長的計算時間嚴重影響優化設計效率[2-3]。

在多組分中子屏蔽材料優化算法設計中[4]，利用遺傳算法選擇優秀個體并交叉、變異產生下一代種群，其中個體的遺傳信息即材質質量組分，而新個體的一個重要評價函數為材料屏蔽效果，通常需要利用蒙特卡羅計算。為減少時間消耗，開展了利用神經網絡算法實現快速屏蔽計算的應用研究。該方法將所有可能的材料組分方案看做是一個輸入空間，各個方案對應的屏蔽計算結果作為輸出空間；選擇空間有限數量點組成訓練樣本，通過神經網絡學習得到預測模型，建立輸入空間到輸出空間代數擬合的映射關系；在應用于遺傳算法迭代過程中時，對于輸入空間的任意材料組分方案，利用此預測模型可代數運算快速獲得屏蔽計算結果，無需再調用蒙特卡羅模擬程序。

神經網絡預測方法在提高計算速度的同時犧牲了一部分蒙特卡羅方法的屏蔽計算精度，二者計算結果的偏差與樣本的數量和全局性、網絡參數、訓練模式以及問題本身的內在邏輯性都有關系。計算結果的偏差范圍和分布、精度控制、泛化能力等是該方法能否應用于遺傳算法的關鍵，本文就此對建立的BP神經網絡預測模型和結果進行了討論，并進一步分析了有限樣本下交叉驗證法訓練模式對預測偏差的改善程度。

1 多組分材料及中子屏蔽計算

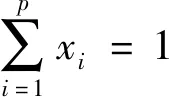
不同材料組分方案具有不同的屏蔽效果，利用蒙特卡羅模擬方法評估復合材料的中子屏蔽效果。材料結構設為30 cm等厚平板，半徑為50 cm；中子源項為Watt裂變譜描述的252Cf單向面源；利用蒙特卡羅程序計算單位注量的中子穿過復合材料構成的平板結構后的中子和次級光子周圍劑量當量之和D(平均劑量×材料面積，量綱：pSv·cm2)來表征屏蔽效果。

2 神經網絡算法實現

2.1 BP神經網絡簡介

BP神經網絡是一種按誤差逆傳播算法訓練的多層前饋網絡，典型的三層BP網絡模型拓撲結構包括輸入層、隱層和輸出層，如圖1所示。層與層之間利用傳輸函數關聯計算，其輸入矩陣X、網絡權值矩陣Ω、閾值向量b、激活函數f和輸出矩陣Y的關系如下：

Y=f2[Ω2f1(Ω1X+b1)+b2]

(1)

神經網絡訓練過程中，根據實際輸出與期望輸出，以降低誤差性能函數為目標，逐步迭代調整各層的權值和閾值，直到網絡訓練達到預設次數為止。常用的誤差性能函數為均方誤差，其總誤差性能函數為：

(2)

式中，ti為目標矢量(本文相當于劑量和D)，yi(k)為第k次迭代后的輸出矢量(相當于預測的劑量和D)。

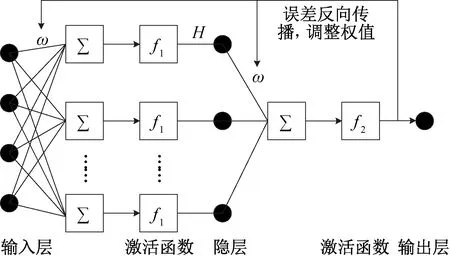
圖1 BP神經網絡基本結構Fig.1 Basic structure of BP neural network

2.2 構建BP神經網絡

BP神經網絡方法學習和訓練的對象為輸入矩陣和輸出矩陣的映射關系：訓練樣本以材料各組分的質量分數數據為輸入，隨機抽樣構造了300組不同的材料組分方案并檢驗其分布均勻性；使用蒙特卡羅程序計算各組分方案下射線穿過材料后的劑量之和D作為輸出。基于Matlab神經網絡工具箱，構建BP神經網絡進行訓練，具體流程如圖2所示。

(1)樣本代表性

輸入空間理論上是無限大的，用于網絡學習和訓練的樣本是從輸入空間中隨機選取的一部分點集，其分布均勻性和全局性關系到最終獲得的網絡模型的泛化能力。對應于6種材料質量組分，輸入空間為一個6維空間，訓練樣本點為6維矢量，通過比較300個樣本中各組分數據統計分布的一致性，定性判斷樣本的代表性。如圖3所示，樣本中6種組分數據值的分布基本一致，認為樣本是隨機均勻的。

訓練樣本中一部分用來訓練網絡(90%)，另一部分用作測試驗證(10%)，用于訓練過程中的網絡泛化性檢驗。

(2)網絡參數設置

利用神經網絡工具箱提供的預設算法函數等，經調試比較建立的網絡結構如下：采用一個隱層；隱層節點數是中間變量的個數，一般基于經驗和調試進行設置，節點數太大會導致過擬合，而且對本文算例并不能顯著提高訓練效果，經比較隱層節點數設置為29。

激活函數將非線性引入到網絡中，使得神經網絡可以任意逼近任何非線性函數；在輸入量加權求和后，利用激活函數獲得下一層的輸出；tan-sig mod(雙曲正切S型)型傳遞函數的輸入值可取任意值，輸出值在-1到+1之間，見式(3)；經比較網絡訓練效果，輸入層和輸出層的激活函數均選擇tansig函數:

(3)

訓練精度和收斂性對初始權重賦值敏感，使用均值為0、標準差為0.001的正態分布隨機數作為初始化權重值能有效加快收斂速度。

訓練函數根據誤差性能函數調整權值閾值，選擇Levenberg-Marquardt(trainlm)算法，該算法在最小二乘擬合過程中修改權值參數時結合了高斯-牛頓算法以及梯度下降法的優點，能獲得較好的收斂結果。

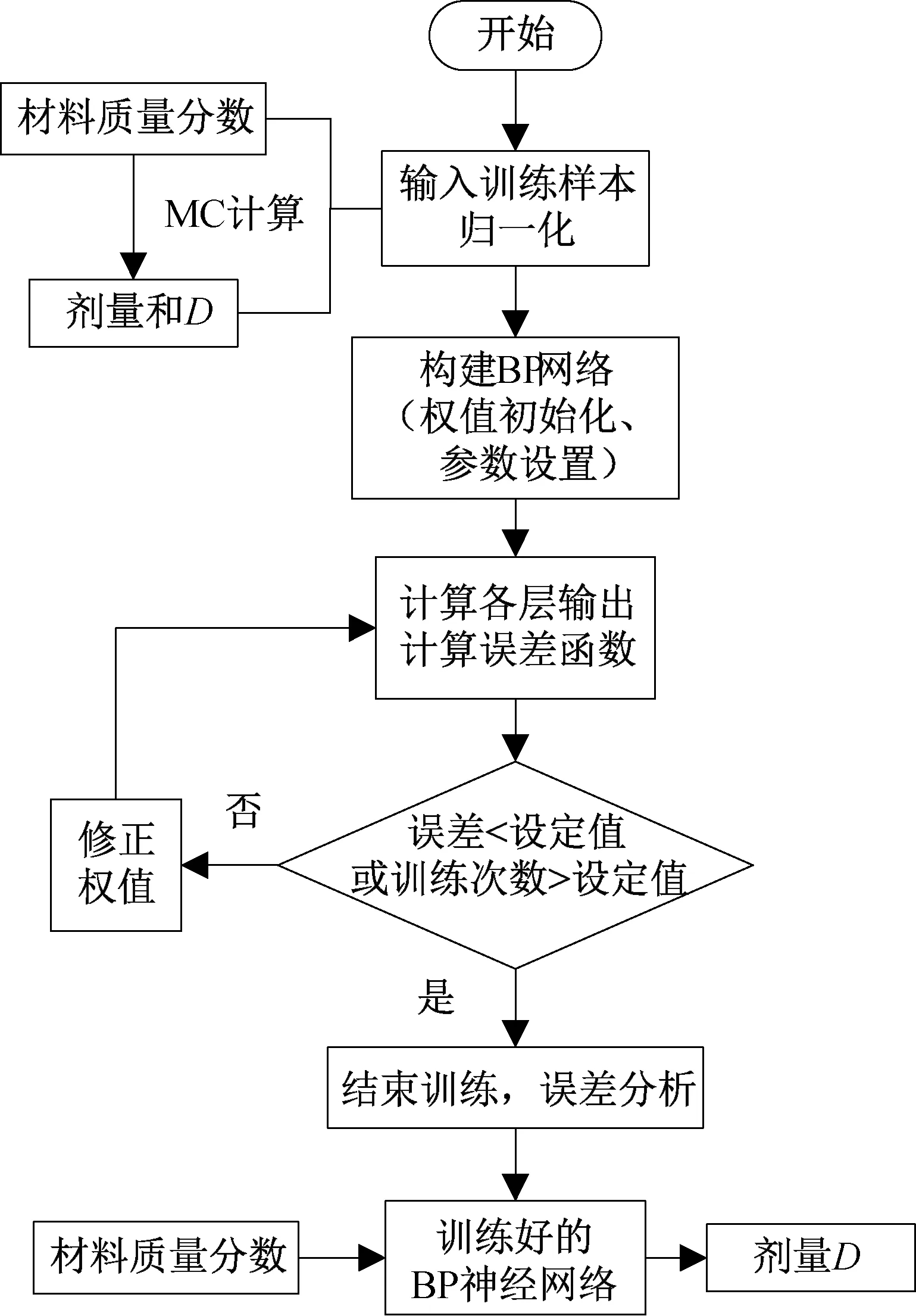
圖2 神經網絡訓練和預測流程圖Fig.2 Training and prediction flow chart of Neural network

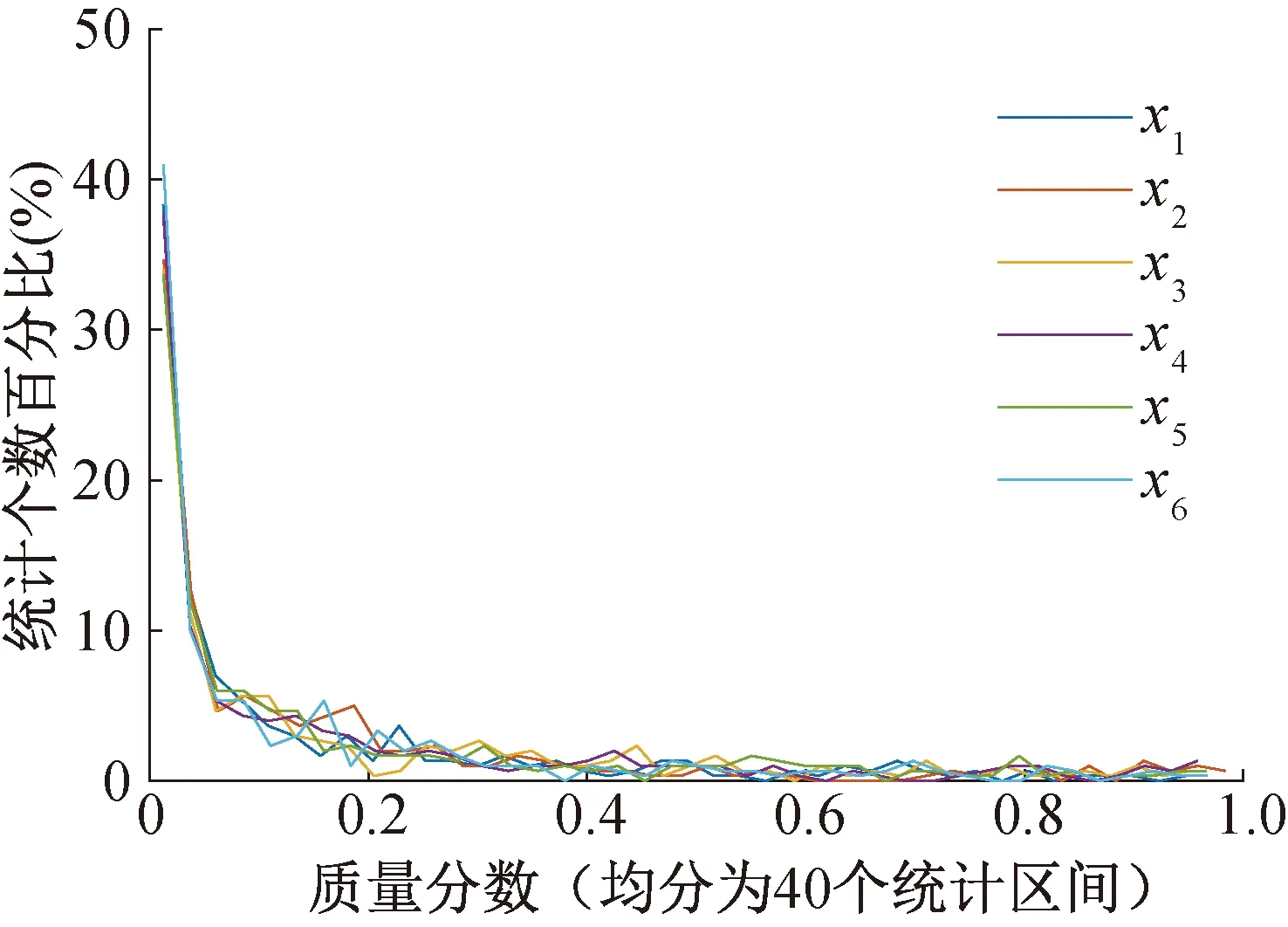
圖3 樣本中質量組分統計分布Fig.3 Statistical distribution of mass components in training samples

2.3 訓練結果

經訓練該神經網絡模型可快速收斂，最終獲得的模型對樣本的線性回歸總相關系數大于0.9999。如圖4所示，比較了利用該模型和訓練樣本質量組分計算得到的劑量值D(實際輸出)與預期值(初始蒙卡計算結果)，直觀顯示相對偏差大部分在±10%以內，個別樣本的相對偏差絕對值接近20%。

為觀察偏差的分布規律，圖中樣本點按劑量值由低到高排序顯示。可見在低劑量段相對偏差較大，高劑量段相對偏差較小，而絕對偏差整體在±2以內；絕對偏差相比于相對偏差分布更加均勻。這是因為上述BP神經網絡訓練過程以式(2)的均方差為誤差性能評價函數，而不是相對誤差所導致的。

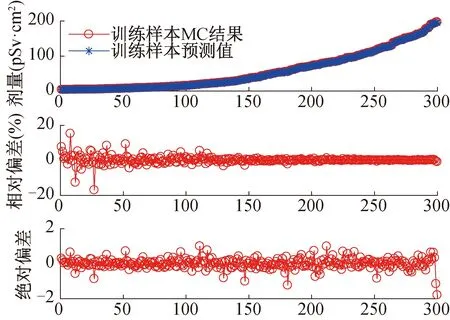
圖4 BP神經網絡預測結果與蒙卡計算結果的對比Fig.4 The results comparison of BP neural network and monte carlo

多組分中子屏蔽材料組分優化算法中，利用該訓練好的BP神經網絡模型計算遺傳算法迭代中新種群個體的劑量值D，其目標是通過搜索將種群的劑量值整體降低至最低。該神經網絡預測結果的絕對偏差較小，因此計算精度不會較大影響遺傳算法的搜索尋優方向，而且通過在遺傳算法評價函數中基于偏差估計設置置信范圍，可進一步控制種群的多樣性，避免因劑量值預測誤差導致的過早收斂或陷入局部最優[4]。最終尋優結果可能因為神經網絡計算偏差而無法到達真正最優解，但也是與最優解非常接近的。

事實上對于該方法，相比于神經網絡模型對訓練樣本的計算偏差，其泛化能力才是保持尋優正確方向更關鍵的因素，即對輸入空間訓練樣本之外的任意點(質量組分方案)的劑量值能夠保持相當預測精度更為重要。隨機重新構造了330組不同的質量組分并使用蒙特卡羅程序計算劑量D，作為驗證樣本；將驗證樣本質量組分帶入訓練好的神經網絡模型中計算出劑量預測值，與蒙卡計算值的比較如圖5所示(樣本按劑量值由低到高排序顯示)，其相對偏差仍在±20%以內，為-16.8%～18.8%之間；絕對偏差為-6.4～5.2之間。

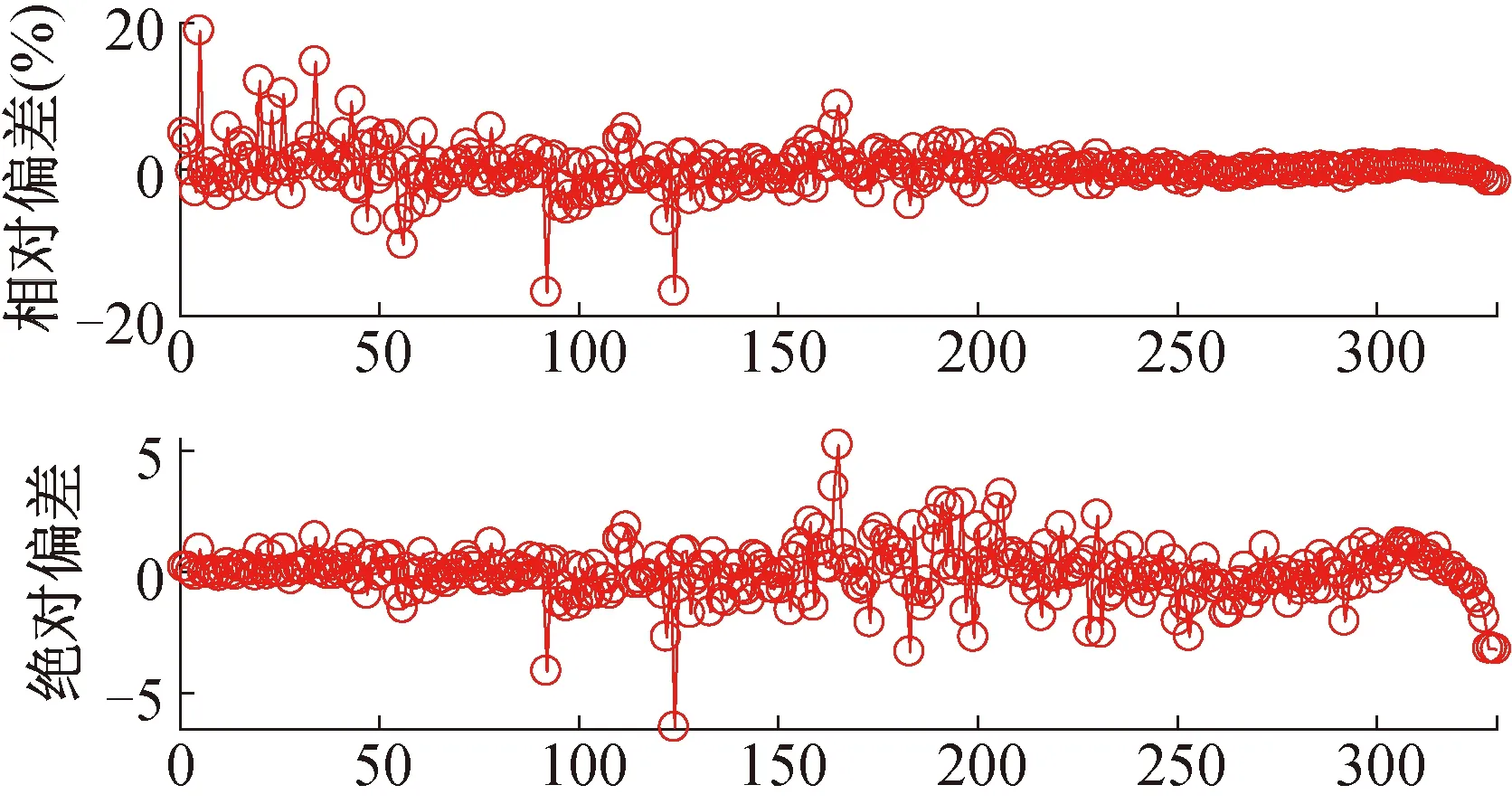
圖5 驗證樣本神經網絡預測結果與蒙卡結果的偏差Fig.5 The results comparison of BP neural network and monte carlo for verification samples

如圖6所示對訓練樣本和驗證樣本的預測相對偏差絕對值進行分段統計，從整體分布上看驗證樣本的相對偏差相比于訓練樣本有所擴大，但70%以上樣本的相對偏差絕對值仍在2%以內。從泛化能力看該模型滿足遺傳算法使用，偏差分布規律的分析可以為優化算法中評價函數置信范圍的設置提供參考。

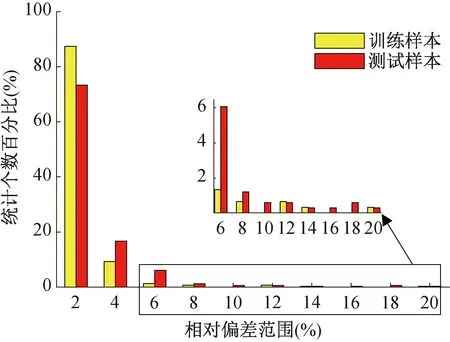
圖6 相對偏差絕對值統計分布Fig.6 Statistical distribution of absolute relative deviation

3 訓練模式影響分析

上述BP神經網絡模型訓練過程中，設置了10%的訓練樣本用作測試驗證。在初步訓練的結果上，采用交叉驗證法對模型進行二次訓練，以比較訓練模式對獲得的神經網絡模型性能的影響。交叉驗證法將訓練樣本打亂并均勻分成K份，輪流選擇其中K-1份訓練，剩余1份驗證，在樣本數量較少時可以一定程度提高學習和訓練效果。

交叉驗證法訓練后新的網絡模型對訓練樣本劑量值D的預測偏差顯著降低，如圖7所示(按劑量值由低到高排序顯示)，與蒙特卡羅計算的預期值相比絕對偏差縮小到±1以內，相比于圖4，相對偏差也明顯降低。

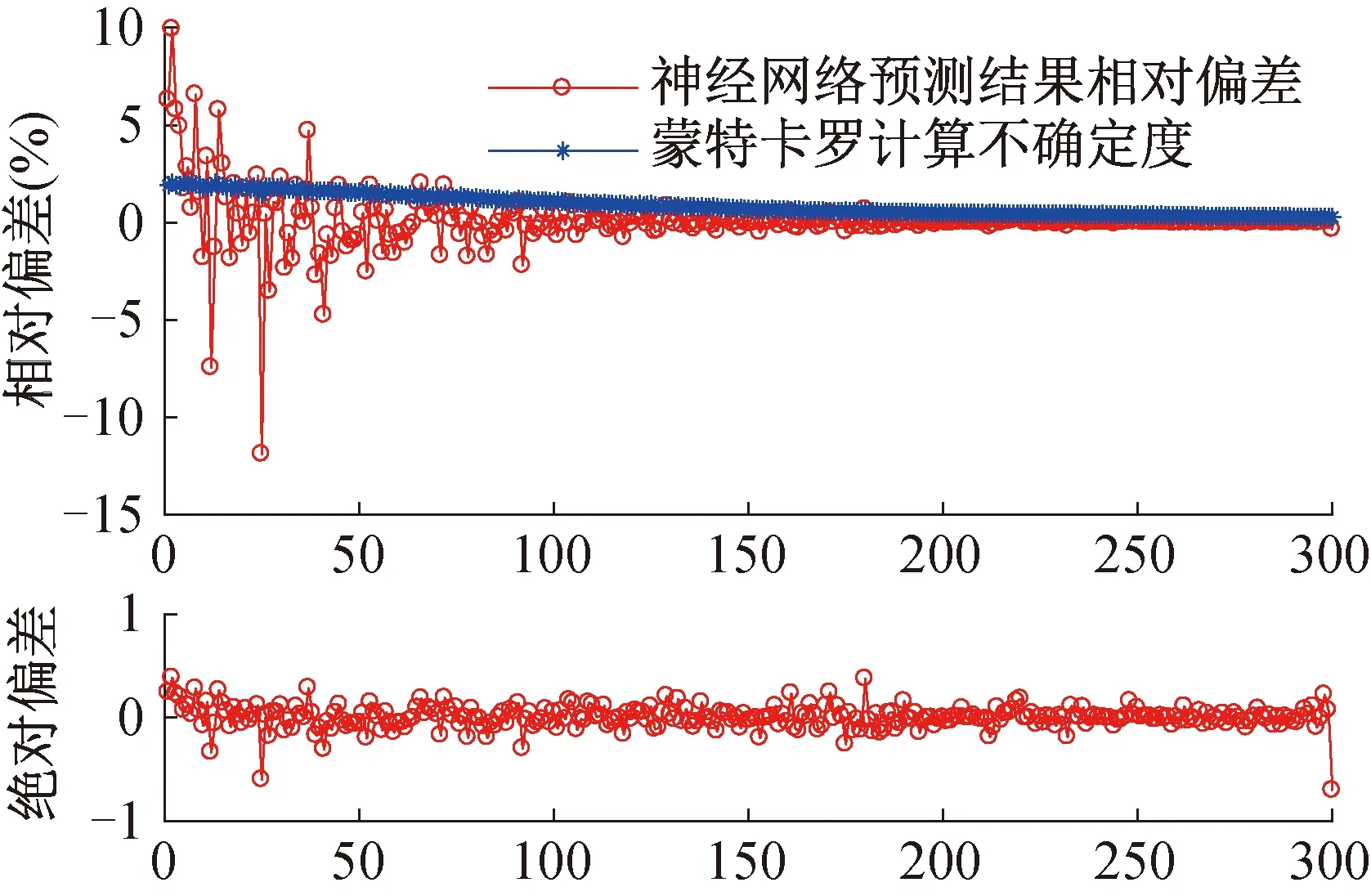
圖7 交叉驗證法預測結果與蒙卡計算結果的對比Fig.7 The results comparison of cross-validation BP neural network and monte carlo

圖7藍色點為訓練樣本劑量值D蒙卡模擬計算的相對不確定度，BP神經網絡預測偏差的變化趨勢和其有一致性，說明訓練樣本自身映射關系的不確定度也是限制最終BP神經網絡模型訓練精度的重要因素。

同樣利用前述330組驗證樣本對交叉驗證法獲得的網絡模型進行泛化性能測試。劑量預測值與蒙卡計算值的比較如圖8所示，其相對偏差在-10.38%～16.68%之間；絕對偏差在-9.09～6.76之間。

圖8結果與圖5結果比較說明，交叉驗證法二次訓練獲得的新的神經網絡對驗證樣本劑量值的預測相對偏差有所減少，但絕對偏差有所擴大。說明神經網絡模型對訓練樣本空間的偏差水平不代表全樣本空間，還需考慮其對驗證樣本空間的偏差水平。盡管交叉驗證法提高了訓練樣本的預測精度，但對驗證樣本的預測反而一定程度有所變差；某種程度上訓練樣本偏差范圍控制的越小越可能容易導致過擬合，使得模型對全樣本的適應性和泛化能力提高程度有限甚至下降。

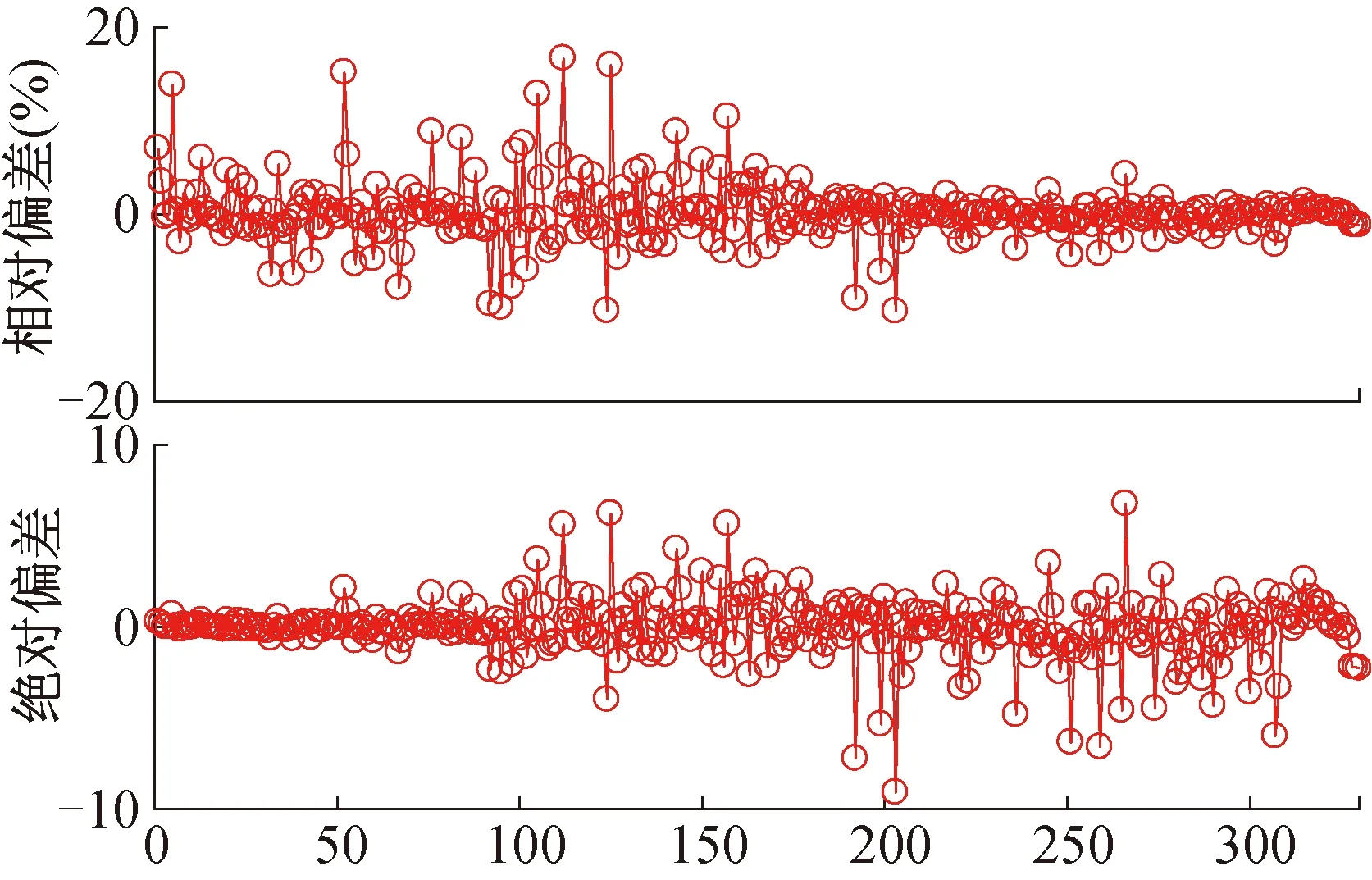
圖8 驗證樣本交叉驗證法神經網絡預測結果與蒙卡結果的偏差Fig.8 The results comparison of cross-validation BP neural network and monte carlo for verification samples

4 結論

本文探索了BP神經網絡方法用于多組分材料中子屏蔽效果快速預測的可行性，利用隨機構造和蒙特卡羅計算的300組訓練樣本能夠快速建立收斂性較好的神經網絡模型，其對訓練樣本的劑量值預測結果與蒙卡計算值基本吻合，絕對偏差整體能控制在±2以內。而且該網絡模型對訓練樣本之外構造的驗證樣本同樣有較好的泛化性，絕對偏差雖有所擴大，但保持在-6.4～5.2之間。驗證樣本的精度和偏差范圍原則上可看做是全樣本空間的精度和偏差范圍，因此從泛化能力和偏差分布看，該方法滿足基于遺傳算法的中子屏蔽材料優化設計使用，可以為其劑量值評價函數提供快速計算模塊。

訓練樣本數量是有限的，而樣本空間理論上無限大，提高計算精度和泛化能力是有限樣本下神經網絡算法實現過程的主要目標。采用交叉驗證法進行二次訓練結果顯示，該方法獲得的網絡模型對訓練樣本的計算精度有明顯提高，但對驗證樣本的計算精度在一定程度有所變差。因此，限于訓練樣本數量、分布以及自身不確定性等，樣本的擬合程度和泛化能力有一個平衡點。