基于嵌套思路的飽和孔隙-裂隙介質本構理論

胡亞元

（浙江大學 濱海和城市巖土工程研究中心，浙江 杭州 310058）

自然界中，許多巖土材料具有兩種不同尺度的孔隙，如裂隙黏土和巖體等.一種孔隙尺度比較小，通常仍稱為孔隙，另一種孔隙尺度比較大，通常呈裂縫或扁平狀，被稱為裂隙.當孔隙和裂隙同時被一種流體占有時，就形成飽和孔隙-裂隙介質.近年來，隨著水利水電、海底隧道、核廢料儲存以及海洋能源開發等工程大量建設，為了分析滲流和變形的流固耦合特性，飽和孔隙-裂隙介質的本構模型研究愈來愈受到工程力學界重視.Barenblatt 等[1]首先研究飽和孔隙-裂隙雙重孔隙介質的本構特性.Khalili 等[2]、劉耀儒等[3]建立了各向同性飽和孔隙-裂隙介質的線彈性模型.蔡國慶等[4]和Zhao 等[5]建立了各向異性飽和孔隙-裂隙黏土的本構理論.張玉軍等[6]創建了考慮裂隙產狀等幾何特性的孔隙-裂隙巖體的彈塑性模型.這些開創性成果有力地促進了飽和孔隙-裂隙介質力學本構理論的發展和應用.

在當前飽和孔隙-裂隙介質本構建模的研究文獻中，針對同一個工程問題往往會創建出多種差異懸殊的本構模型.如何在各種模型中選擇適合的飽和孔隙-裂隙介質本構模型成為工程師和學者首先遇到的難題.混合物理論從普適性的力學守恒定理出發研究孔隙-裂隙本構理論的普遍規律，具有嚴密的邏輯結構和明確的物理內涵，許多學者建議把混合物理論作為判定其他本構模型合理性的理論依據之一[7-11].Borja 等[7]和Zhang 等[8]根據混合物理論推導了飽和及非飽和孔隙-裂隙介質的能量平衡方程，并建立了飽和孔隙-裂隙介質線彈性本構模型，但該模型無法考慮裂隙與孔隙流相壓力之差所導致的固相體積變化.Li 等[9-10]基于混合物理論推導了非飽和雙孔隙膨脹土的外力功表達式，建立了非飽和雙孔隙膨脹土的彈塑性本構模型；Guo 等[11]采用混合物理論建立了飽和及非飽和孔隙-裂隙介質的雙有效應力彈塑性模型.然而，這些模型沒有考慮固相和流相的材料變形，只適用于土體松散介質，無法適用于巖石和混凝土等非松散孔隙-裂隙介質[12-16].為了彌補上述缺陷，深刻揭示孔隙骨架應變和裂隙骨架應變在多孔介質流固耦合機制中的關鍵作用，便于利用均勻化響應原理相來建立相對簡單實用的本構模型[14]，有必要對飽和孔隙-裂隙介質混合物理論作進一步深入研究.

鑒于此，筆者發現孔隙-裂隙介質可視為兩個單重孔隙介質的嵌套疊加，即孔隙-裂隙介質可視為在單重裂隙介質的固相基質中嵌套了一個單重孔隙介質.本文從這一嵌套思路出發來研究飽和孔隙-裂隙介質的能量守恒方程和一般本構模型理論框架，從一般本構模型理論出發可推導飽和雙重孔隙介質的線彈性方程，指導和校正當前飽和孔隙-裂隙介質的本構建模工作.

1 體積分數和密度

1.1 飽和孔隙-裂隙介質各組分體積分數和密度

飽和孔隙-裂隙介質是由固相、裂隙流相與孔隙流相組成的混合物.固相由S 表示，裂隙流相由F 表示，孔隙流相由P 表示.令α∈{S，F，P}為組分指征變量.φα為第α 組分的體積分數，ρα為第α 組分的平均密度，ρα為第α 組分的真實密度（或稱材料密度），滿足ρα=φαρα，則飽和孔隙-裂隙介質的總密度為ρ=ρS+ρF+ρP.根據體積分數的定義有：

1.2 基于嵌套思路的各組分體積分數和密度

本文把固相材料與孔隙流相組成的飽和單重孔隙介質稱為飽和孔隙介質.當把飽和孔隙-裂隙介質中的固相材料和孔隙流相所構成的飽和孔隙介質視為一個整體時，此時只有裂隙被視為孔隙，本文把這種視角下的廣義飽和單重孔隙介質稱為飽和裂隙介質.這樣，飽和孔隙-裂隙介質可看作在飽和裂隙介質的基質中嵌入飽和孔隙介質而成，而飽和孔隙-裂隙介質可視為兩個單重孔隙介質的嵌套疊加.

根據上述嵌套思路，首先考慮飽和裂隙介質.飽和孔隙介質作為飽和裂隙介質的一個組分用SP 表示，它的體積分數為固相和孔隙流相體積分數之和φSP=φS+φP.根據式（1），在飽和裂隙介質中有：

然后考慮飽和孔隙介質.令β∈{S，P} 為飽和孔隙介質的組分指征變量，當飽和孔隙介質視為一個獨立混合物時，則第β 組分在飽和孔隙介質中的體積分數為為飽和孔隙介質中固相的平均密度，則在飽和孔隙介質中有：

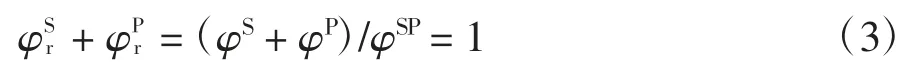
2 質量與動量守恒

2.1 質量守恒

令第α 組分的初始位置為Xα，t 時刻的空間位置為x，則每一組分的運動方程為x=xα（Xα，t），每一組分的速度和加速度可表示為：

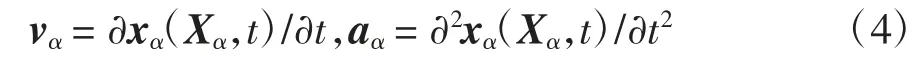
對于定義在x 和t 上的標量場或矢量場Γα，基于α 組分的物質導數的定義為：

由于固相與裂隙中的流相、固相與孔隙中的流相均不存在質量交換，而裂隙中的流相和孔隙中的流相之間存在質量交換，則固相、裂隙流相與孔隙流相的質量守恒方程為：

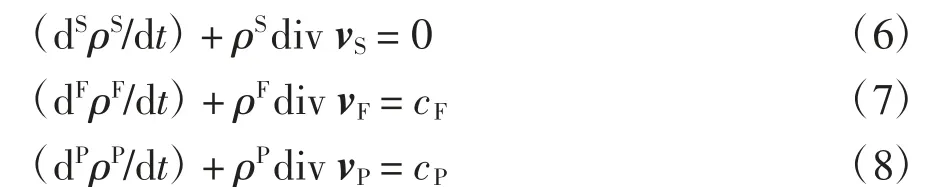
式中：cF和cP分別表示裂隙流相與孔隙流相之間的質量交換率，滿足cF+cP=0.

把固相作為飽和孔隙-裂隙介質混合物的參考構形，令裂隙流相和孔隙流相相對固相的擴散速度分別為WF=vF-vS和WP=vP-vS.把WF、WP、式（5）和ρα=φαρα代入式（6）～（8）得：

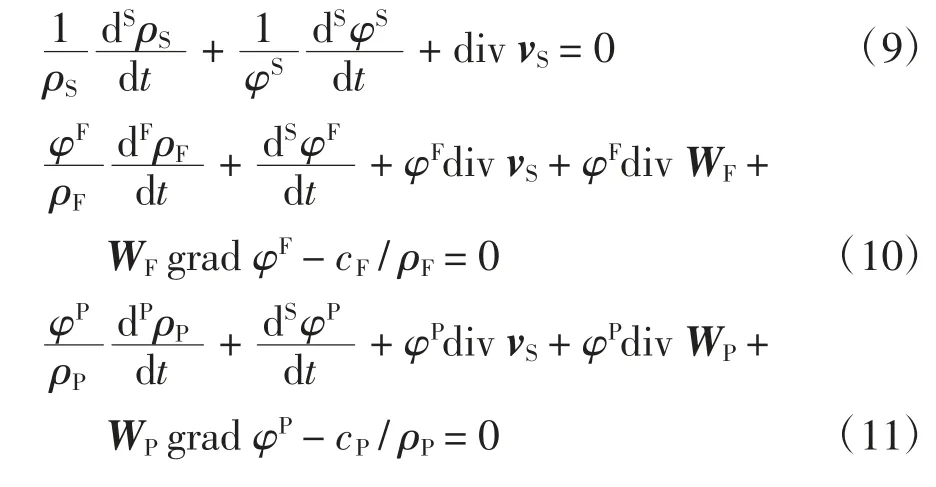
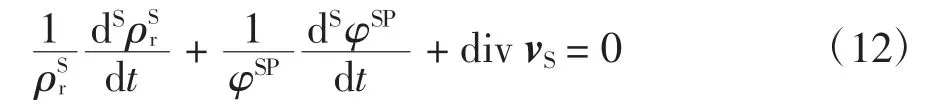
令div vr為飽和孔隙介質整體的體積變形率，與式（6）相類似，根據飽和孔隙介質中的質量守恒定律，有

將式（13）代入式（12）得：

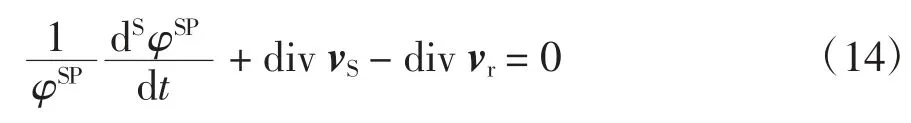
2.2 動量和動量矩守恒

2.2.1 飽和孔隙-裂隙介質的Cauchy 應力張量

在飽和孔隙-裂隙介質混合物中，令σ 為混合物總Cauchy 應力張量，σα（α∈{S，F，P}）為第α 組分的Cauchy 應力張量，根據混合物理論有[7，16]

令總壓力PT=-σ ∶I/3.固相材料真實壓力PS與σS之間滿足φSPS=-σS∶I/3，裂隙壓力PF和孔隙孔壓PP與其應力的關系滿足φFPFI=-σF和φPPPI=-σP，利用上述關系和式（15）得：

根據嵌套思路，先考慮飽和裂隙介質.飽和孔隙介質作為飽和裂隙介質的組分，它的Cauchy 應力張量等于σSP=σS+σP.飽和裂隙介質總應力和各組分應力之間的關系由式（15）得：

令PSP=-σSP∶I（/3φSP）為飽和孔隙介質所受的真實壓力，飽和裂隙介質總壓力和各組分壓力之間的關系由式（17）得：

再考慮飽和孔隙介質.如圖1（c）和（d）所示，把飽和孔隙介質取為單元體，則固相和孔隙流相組分的Cauchy 應力張量分別為σrS=σS/φSP和σrP=σP/φSP，飽和孔隙介質混合物總應力張量為σr=σrS+σrP=σSP/φSP.故飽和孔隙介質在單元體上的總應力等于它在飽和裂隙介質中的真實應力，因而PSP=-σr∶I/3.飽和孔隙介質總壓力和各組分壓力之間的關系為：

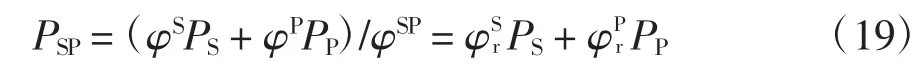
圖1 給出了飽和孔隙-裂隙介質總壓力與各組分壓力關系式.

圖1 飽和孔隙-裂隙介質特征單元體示意圖Fig.1 Schematic diagram for the representative volume element of saturated pore-fracture media

從圖1 可以看出，圖1（a）表示總壓力PT作用在飽和孔隙-裂隙介質單元體上，圖1（b）表示了式（16）和式（18）反映的飽和孔隙-裂隙介質和飽和裂隙介質的壓力關系式，圖1（c）表示PSP作用在飽和孔隙介質單元體上，圖1（d）表示了式（19）反映的飽和孔隙介質的壓力關系式.

2.2.2 飽和孔隙-裂隙介質的動量和動量矩守恒

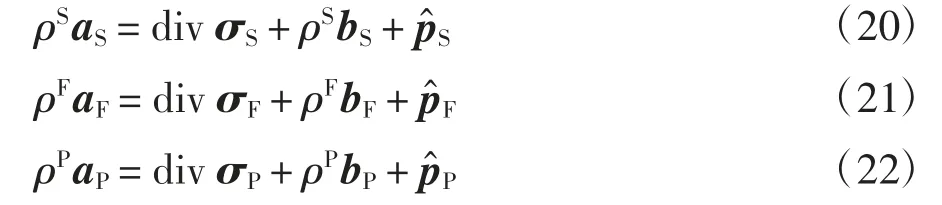
工程界為便于應用，通常不考慮飽和孔隙-裂隙介質的微極介質特性，故第α 組分的動量矩供應量為0，利用固相、裂隙流相和孔隙流相的動量矩守恒方程可得應力張量σα（α∈{S，F，P}）是對稱張量.

3 能量平衡方程

3.1 能量平衡方程

令qα、rα和分別為第α 組分的熱流向量、外熱供給量和能量供給量，ξα為第α 組分的內能密度，則固相、裂隙流相和孔隙流相的能量平衡方程為：

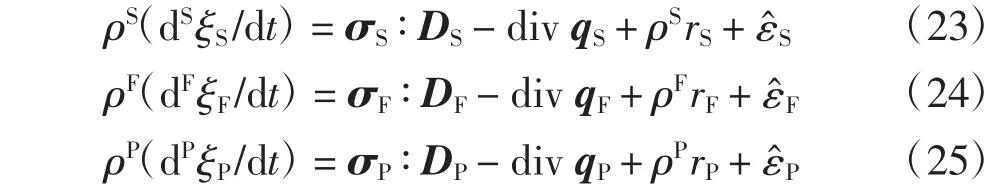
式中：DS=[grad vS+（grad vS）T]/2 為固相變形率；DF=[grad vF+（grad vF）T]/2 為裂隙流相變形率；DP=[grad vP+（grad vP）T]/2 為孔隙流相變形率.把式（23）～（25）相加可得：

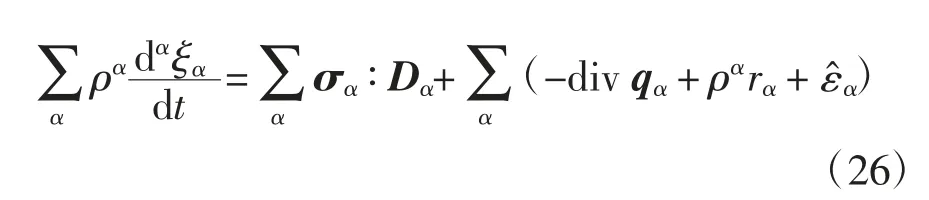
從式（26）可知，等號右側第一項的物理含義為各組分應變能變化率之和，利用σF=-φFPFI、σP=-φPPPI、WF和WP，各組分應變能變化率之和可得：

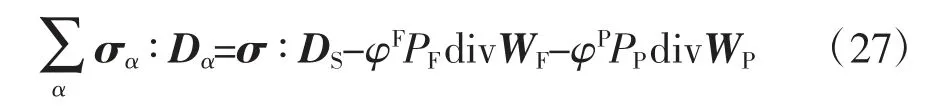
根據嵌套思路，先考慮飽和裂隙介質.令飽和裂隙介質Terzaghi 有效應力為=σ+PFI，利用式（2）、式（10）、式（13）和div vS=I ∶DS，把式（27）等式右邊的前兩項替換后可得：

式（32）表明DH的球應變速率與孔隙介質在裂隙介質中的體積分數相關.孔隙介質是裂隙介質的基質，在裂隙介質中起到骨架作用，因此本文把DH稱為裂隙骨架變形率.式（34）表明DH的球應變速率與裂隙比改變率亦直接相關，即DH也可以采用裂隙介質的裂隙比來定義.同理，根據式（33）和式（35），DD可稱為孔隙骨架變形率.把DD=Dr+（dS?S/dt）I/3 和DH=DS-Dr代入式（31）后再把它代入到式（26）得：

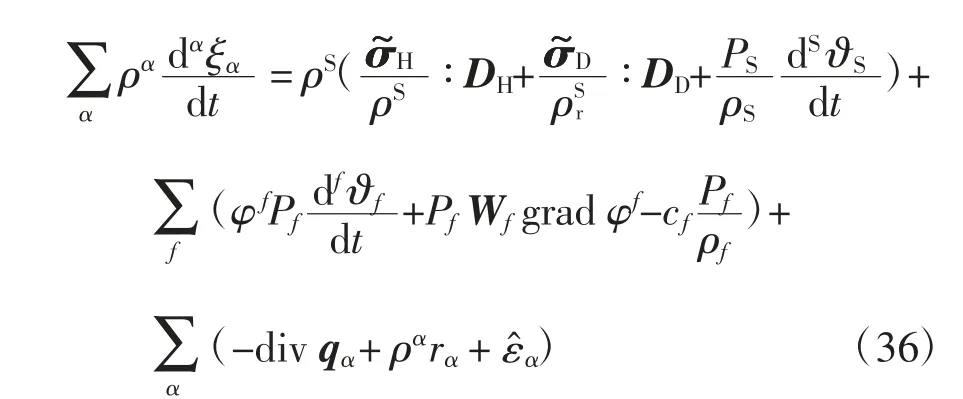
在式（36）中，固相變形率DS被分為三部分：裂隙骨架變形率DH，孔隙骨架變形率DD和固相材料體應變率dS?S/dt.在式（36）中，DH、DD、dS?S/dt、dF?F/dt 和dP?P/dt 分別與和PP/ρF形成功共軛對.由熱力學理論可知，在一般情況下，應選取裂隙骨架應變、孔隙骨架應變、固相材料體應變、裂隙流相材料體應變和孔隙流相材料體應變作為飽和孔隙-裂隙介質本構模型的應變狀態變量；選取單位密度上的裂隙介質有效應力、孔隙介質有效應力、固相材料真實壓力、裂隙孔壓和孔隙孔壓作為應力狀態變量.

3.2 混合物均勻化響應原理

為了適應工程應用，工程界常常利用混合物均勻化響應原理來簡化混合物的本構關系.混合物均勻化響應原理的內容為[14]：當混合物單元體承受外荷載時，若混合物單元體中每一點的真實應變增量（或速率）相等，則該混合物單元體等效于單相均勻單元體，即單元體內每一點處的真實應力增量（或加荷速率）也相等；反之也然.在Khalili 等[2]、陳正漢[17]、陳勉和陳至達[18]推導各種飽和和非飽和混合物本構關系時，混合物均勻化響應原理曾發揮了至關重要的作用.

現在應用混合物均勻化原理對能量平衡方程的合理形式作分析.根據嵌套思路，先應用混合物均勻化原理分析飽和裂隙介質.令裂隙介質有效壓力為∶I/3.在保持總壓力PT與裂隙孔壓PF增速相等的情況下，飽和裂隙介質每一點的真實應力增速相等，此時裂隙介質有效壓力增速為零，但在飽和孔隙介質變形不可忽略的情況下，飽和孔隙介質將產生大小為Dr∶I≠0 的體應變速率.根據混合物均勻化響應原理，飽和裂隙介質每一點應力加荷速率相等時，其應變速率也相等，則飽和裂隙介質的體應變速率為DS∶I=Dr∶I ≠0，故當時DS≠0，這意味著DS不僅與有關還與飽和裂隙介質的其他應力有關，故選取DS作為的功共軛變量不利于飽和裂隙介質的本構建模工作.因為，當dt=0 時，DH=DS－Dr=0，所以本文選取DH作為的功共軛變量，這樣當混合物均勻化原理成立時，DH只與有關而與飽和裂隙介質的其他應力無關，從而根據彈性互易定理可以推斷出DH與其他應變相互解耦的結論.

再應用混合物均勻化響應原理分析飽和孔隙介質.與飽和裂隙介質的分析相類似，當混合物均勻化響應原理成立時，Dr不僅與有關還與飽和孔隙介質的其他應力有關，故選取Dr作為的功共軛變量同樣不利于本構建模工作.由于當時，DD=Dr+（dS?S/dt）I/3=0，故選取DD作為的共軛變量.當均勻化響應原理成立時，同理可以得出Dr與其他應變相互解耦的結論，這也是本文要把應變能寫為式（31）和能量平衡方程寫為式（36）的原因.

3.3 能量平衡方程的退化

式（38）與飽和多孔介質的能量守恒方程完全一致[14].

4 一般勢函數本構方程

4.1 有限應變情況下的一般本構方程

在有限應變情況下，利用連續介質力學[19]中變形梯度的分解方法，先將裂隙介質變形梯度分解為孔隙介質變形梯度與裂隙骨架變形梯度的乘積；后將孔隙介質變形梯度分解為固相材料變形梯度與孔隙骨架變形梯度的乘積，如圖2 所示，圖中F 表示變形梯度.

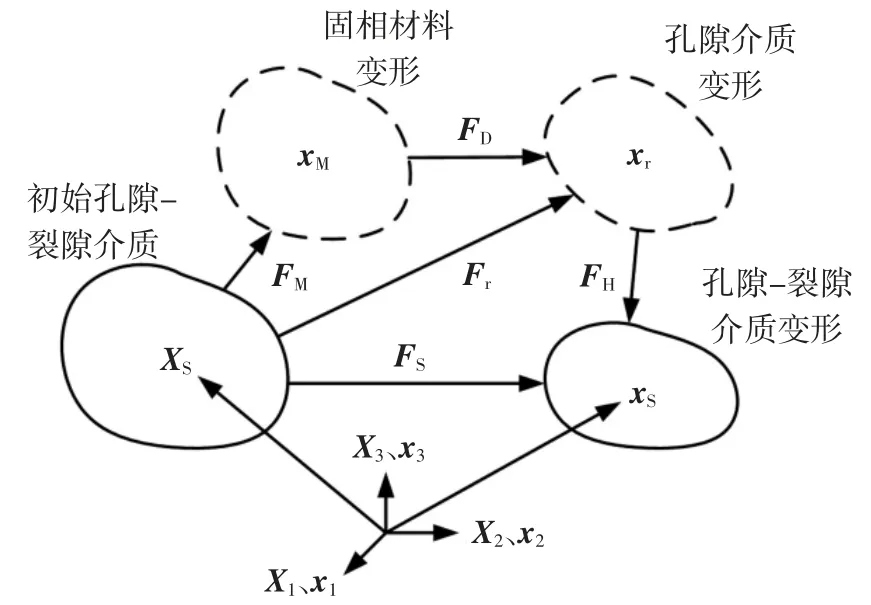
圖2 孔隙-裂隙介質變形梯度示意圖Fig.2 Schematic diagram for the deformation gradient of pore-fracture media

為了工程應用，通常做如下簡化：孔隙-裂隙介質的固相內能、裂隙流相材料內能和孔隙流相材料內能之間相互獨立，即ξS=ξS（UH，ED，?S，ηS），ξF=ξF（?F，ηF）和ξP=ξP（?P，ηP），ηα為各組分熵密度，并假定固相材料、裂隙流相材料和孔隙流相材料具有相同溫度θ.則根據熱力學局部平衡條件以及UH、ED、?S、?F、和?P相互獨立的性質，有

式（40）和式（41）便是有限應變情況下飽和孔隙-裂隙介質的內能勢函數一般本構方程.由于內能是一種自由能，反映的是彈性性質，故式（40）和式（41）為飽和孔隙-裂隙介質的一般彈性本構方程.把式（40）和（41）代入式（39）得：

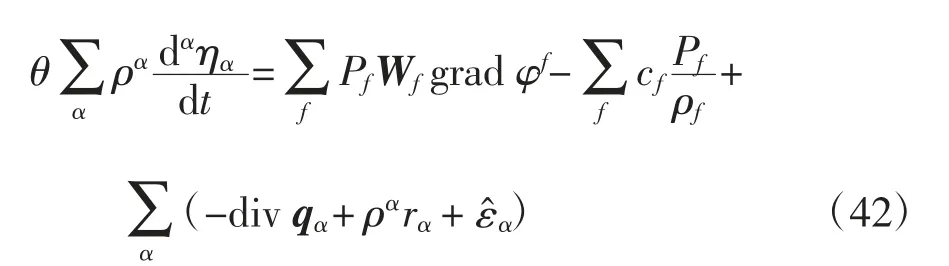
將式（42）與非平衡態熱力學相結合，按照文獻[14]推導過程可進一步獲得飽和孔隙-裂隙介質的塑性本構方程，受篇幅限制本文不再贅述.

4.2 小應變情況下的一般本構方程

4.2.1 小應變情況下各組分應變計算公式

在小應變情況下可略去高次項，令εS為固相應變張量ES的近似值，εH為裂隙骨架應變張量UH的近似值[19]，εr為孔隙介質應變張量Er的近似值，εD為孔隙骨架應變張量ED的近似值，此時得[19]：

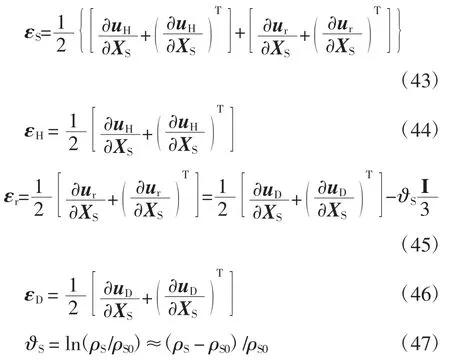
式中：uH=xS-xr，ur=xr-XS，uD=xr-xM，xM是材料變形后的位置.注意到?S以壓為正，ε 以拉為正.對比式（43）～式（47）可得：

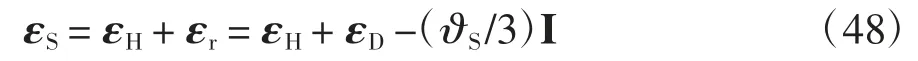
由式（48）可知，在小應變情況下，飽和孔隙-裂隙介質的固相應變εS可以分解為裂隙骨架應變εH、孔隙骨架應變εD與固相材料體應變?S之和.

在小應變情況下，令εSV、εHV和εDV分別為固相、裂隙骨架和孔隙骨架體應變，對式（48）取跡得：

根據式（34）和式（35），可得εHV和εDV的表達式分別為：

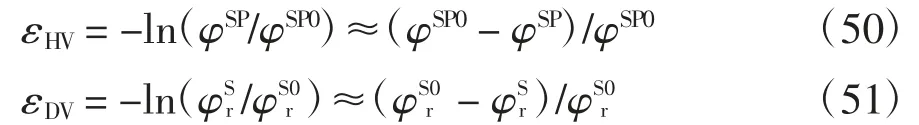
式中：φSP0為飽和孔隙介質整體的初始體積分數：為飽和孔隙介質中固相組分初始體積分數.

接下來推導流相體應變計算式.首先，在小應變情況下，?F和?P可近似地簡化為：

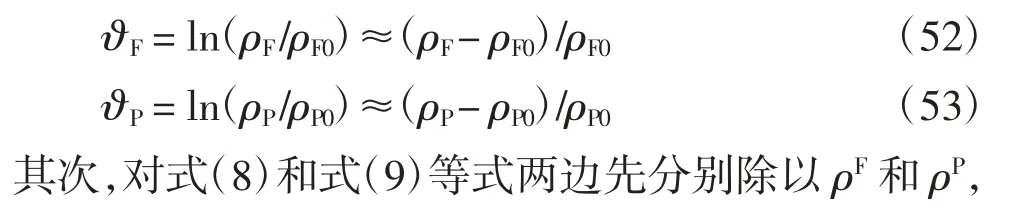
式（58）和（59）便是小應變情況下裂隙流相體應變和孔隙流相體應變的計算式.從式（49）、式（58）和（59）可以明顯地看出，裂隙骨架體應變同時影響固相體應變、裂隙流相體應變和孔隙流相體應變，孔隙骨架體應變同時影響固相體應變和孔隙流相體應變.故固相、孔隙流相和裂隙流相之間必然存在受力變形耦合，它們是通過裂隙骨架和孔隙骨架應變進行傳遞和協同的.

4.2.2 一般本構方程

令ξ*=ρS0ξS+ρF0ξF+ρP0ξP，式中：ρS0為固相初始平均密度；ρF0為裂隙流相初始平均密度；ρP0為孔隙流相初始平均密度.小應變條件下可略去高次項，有

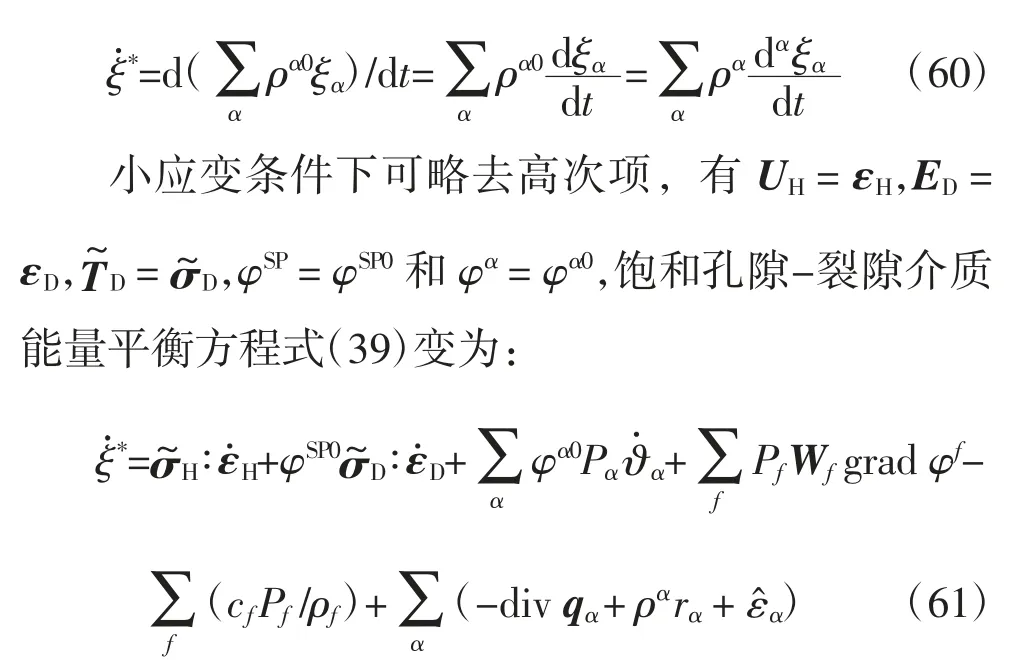
根據熱力學局部平衡假定，式（61）中的內能可表示為ξ*=ξ*（η，εH，εD，?α），對它求全微分得：

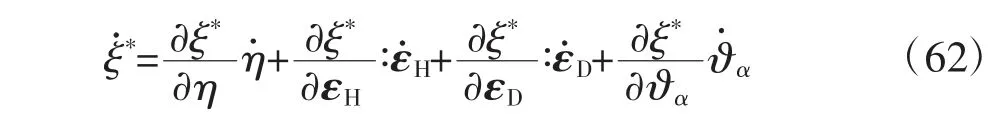
根據熱力學局部平衡假定，對比式（61）和式（62）得：

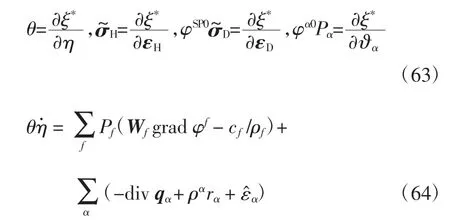
式（63）便是飽和孔隙-裂隙介質在小應變情況下的一般彈性本構方程.將式（64）與非平衡態熱力學相結合，按照文獻[14]的推導過程可獲得飽和孔隙-裂隙介質的塑性本構方程，受篇幅限制，本文不再贅述.

4.3 一般本構方程的退化和驗證

4.3.1 小應變各向同性線彈性本構方程

引入Helmhotlz 自由能ψ*（θ，εH，εD，?α），它等于ψ*（θ，εH，εD，?α）=ξ*（η，εH，εD，?α）-θη，對它求全微分后把式（63）代入得：

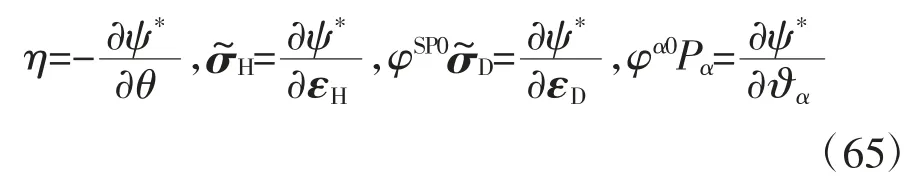
令飽和孔隙-裂隙介質的初始平衡狀態為（θ，εH，εD，?α）=（θ0，0，0，0），在受到微小擾動后，到達一個新的平衡狀態（θ0+θΔ，εH，εD，?α），θΔ為溫度增量.根據勢函數本構方程的一般性質可知，若自由能函數取為狀態變量的二次多項式函數，可獲得線彈性本構關系.故Helmhotlz 自由能取為：

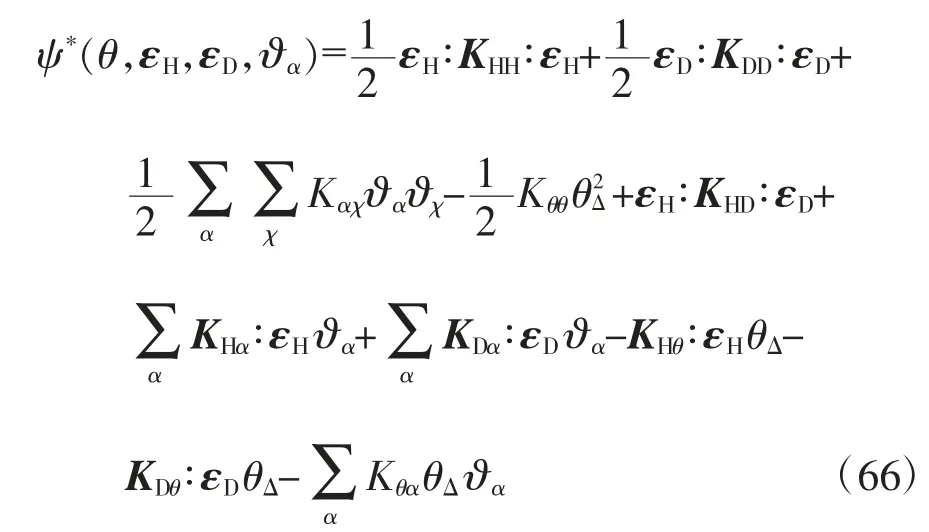
式 中：KHH、KDD、Kαχ、Kθθ、KHD、KHα、KDα、KHθ、KDθ、Kθα為模型的彈性系數；Kαχ=Kχα，α∈{S，F，P}，χ∈{S，F，P}.把式（66）代入式（65）得：

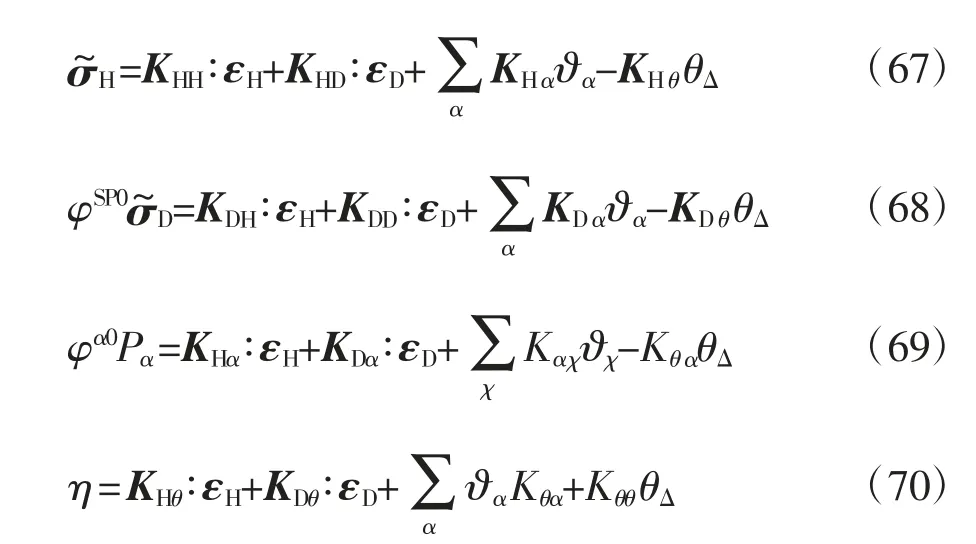
式中：KDH為KHD的轉置.

在當前飽和孔隙-裂隙介質研究中，絕大多數研究均假定：1）溫度不變，即θΔ=0；2）裂隙與孔隙中流相材料的本構關系與其單獨存在時的本構關系相同；3）孔隙骨架和裂隙骨架存在變形耦合；4）固相介質為各向同性材料.由假定2）可知固相變形與流相材料變形相互解耦.根據假定4），KHH和KDD為各向同性張量.根據上述4 個假定，式（67）～式（69）可分別表示為：

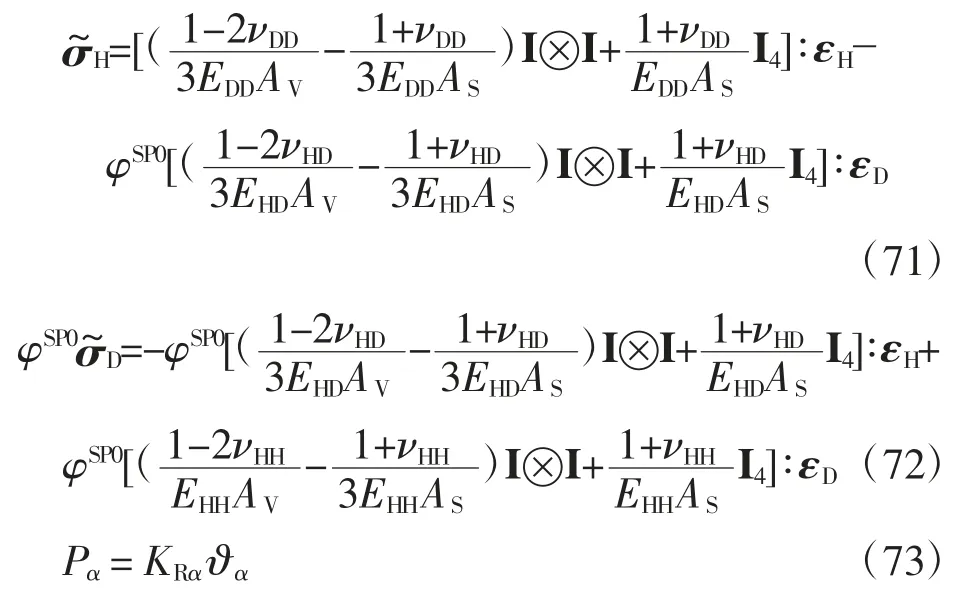
式中：I 為二階單位張量；I4為四階單位張量；νHH為裂隙骨架自身的泊松比；EHH為裂隙骨架自身的彈性模量；νHD為孔隙和裂隙骨架的耦合泊松比；EHD為孔隙和裂隙骨架的耦合彈性模量；νDD為裂隙骨架的泊松比；EDD為孔隙骨架的彈性模量；KRα、α∈{S，F，P}分別為固相材料和流相材料的體積模量.AV和AS分別為：

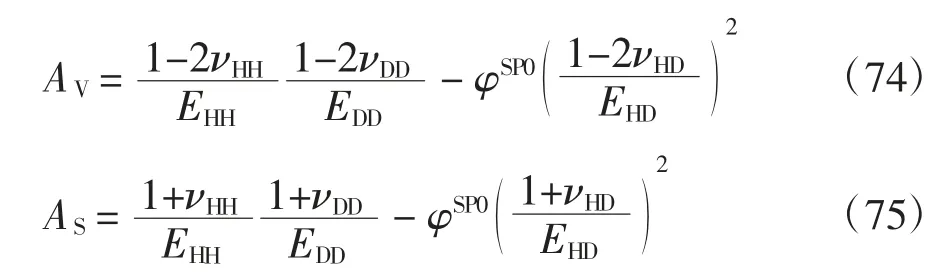
對式（71）和（72）求逆后得：

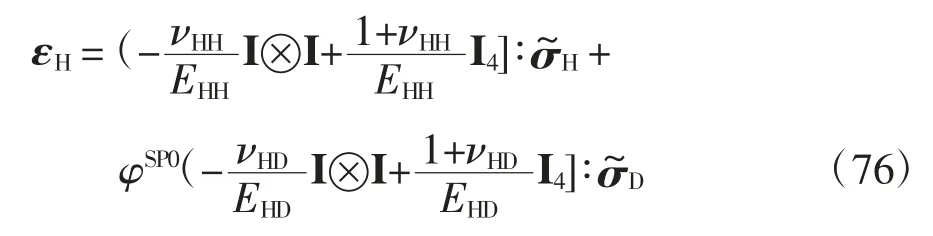
式（84）即為固相線彈性本構方程.對式（84）求跡并利用PT=-σ ∶I/3得固相體應變為：

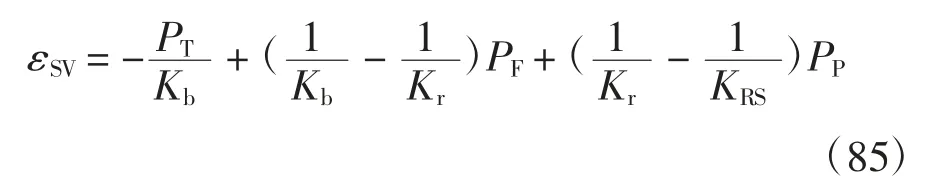
在實際工程中，比較關心的是流體流出或流入孔隙-裂隙介質的流量，定義裂隙流相滲入量為ζF=φF0（εSV-εFV），孔隙流相滲入量為ζP=φP0（εSV-εPV）[20]，利用式（49）、式（58）和（59），ζF和ζP的表達式分別為：

式（88）和（89）分別為本文獲得的裂隙流相和孔隙流相滲入量本構方程.

4.3.2 與Khalili 方程的對比與驗證

Khalili 等[2]假定1/KHD=0，獲得的固相本構方程、裂隙流相滲流方程和孔隙流相滲流方程分別為：

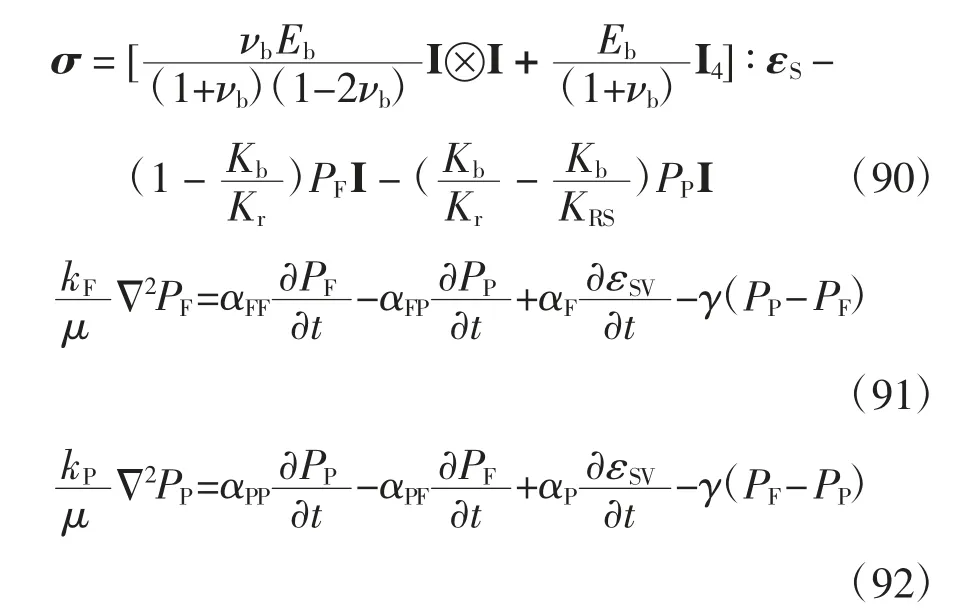
式中：kF和kP分別為裂隙骨架與孔隙骨架的各向同性滲透系數；μ為流相材料的黏滯系數：為拉普拉斯算子.對式（90）求εS關于σ 的反函數可得：

注意到Khalili 等[2]推導式（91）和（92）時假定裂隙和孔隙流相滲流滿足達西定理.根據達西定理可得：

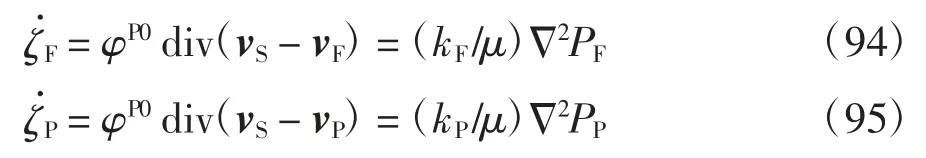
把式（94）和（95）代入式（91）和（92）后求時間積分得：

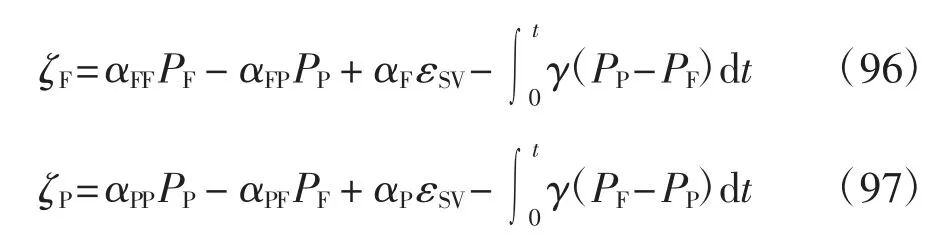
顯然，當1/KHD=0 時，式（84）、式（88）和（89）與式（93）、式（96）和（97）完全一致，說明從本文的自由能勢函數一般本構方程出發可以獲得與Khalili 等相同的線彈性本構模型.Khalili 等把他們的線彈性本構模型用于裂隙黏土的固結分析，獲得了與試驗數據相一致的理論分析結果[2，15].這說明從本文的一般本構方程出發可獲得經過試驗驗證的本構模型.

5 結論

1）在考慮固相和流相材料變形的條件下，以嵌套思路推導了飽和孔隙-裂隙介質的能量平衡方程.確定了飽和孔隙-裂隙介質本構方程的應變狀態變量是裂隙骨架應變、孔隙骨架應變、固相材料體應變、裂隙流相材料體應變和孔隙流相材料體應變；應力狀態變量是單位密度上的裂隙介質有效應力、孔隙介質有效應力、固相材料真實壓力、裂隙孔壓和孔隙孔壓.

2）在小應變情況下，固相應變可分解為裂隙骨架應變、孔隙骨架應變和固相材料體應變之和.獲得有限應變和小應變條件下的飽和孔隙-裂隙介質的自由能勢函數一般本構方程.

3）當混合物均勻化響應原理成立時，裂隙骨架、孔隙骨架和固相材料的本構模型相互解耦；當裂隙與孔隙中流相材料的本構關系與純流相本構關系相同時，固相與流相材料變形相互解耦.當上述兩個性質均成立時，裂隙骨架應變唯一決定裂隙介質有效應力、孔隙骨架應變唯一決定孔隙介質有效應力、固相材料體應變唯一決定固相材料真實壓力、裂隙流相材料體應變唯一決定裂隙孔壓和孔隙流相材料體應變唯一決定孔隙孔壓.運用這些本構性質可以簡化本構關系的復雜程度，有利于工程應用.

4）當自由能勢函數取為狀態變量的二次多項式時，獲得孔隙骨架和裂隙骨架相互耦合的各相同性線彈性本構方程，當孔隙骨架和裂隙骨架變形解耦時，該線彈性方程退化為飽和孔隙-裂隙介質Khalili線彈性方程.Khalili 等利用他們提出的線彈性本構方程獲得與試驗數據相一致的理論分析結果[2，15]，這說明本文基于一般勢函數的本構方程理論框架可以指導飽和孔隙-裂隙介質的具體本構建模工作.