基于改進IMK 恢復力模型的鋼筋混凝土柱參數識別與應用

郭玉榮，龍沐恩

（1.湖南大學 土木工程學院，湖南 長沙 410082；2.建筑安全與節能教育部重點實驗室（湖南大學），湖南 長沙 410082）

鋼筋混凝土框架結構的地震響應混合模擬[1]及其抗倒塌性能的分析，需要可有效模擬鋼筋混凝土構件滯回特征[2]的恢復力模型及準確的模型參數.塑性鉸模型是框架結構非線性模擬常采用的一種模型，它不僅反映構件的力學特征，還與構件的材料、約束狀況及空間布局密切相關.幾十年以來，塑性鉸模型已有了飛速發展，Clough 等[3]開發了雙線性模型；Wen[4]提出了光滑的塑性鉸模型；Takeda 等[5]開發了三線性塑性鉸模型.但是上述常見模型不能充分考慮構件在循環往復荷載作用下的剛度和強度退化，影響了整體結構模擬分析的精確性.Ibarra 等[6-7]開發了復雜的塑性鉸模型即改進的IMK （Ibarra-Medina-Krawinkler）模型.改進IMK 模型作為一種以三折線為骨架曲線的塑性鉸模型，引入了基于能量耗散的退化參數β，考慮了構件在往復荷載作用下的多種剛度和強度退化，相對于其他塑性鉸模型，能夠較好地對鋼筋混凝土梁柱的滯回特征進行有效模擬.但根據模型經驗公式直接計算的改進IMK 模型骨架曲線參數可能會存在明顯的誤差，從而影響框架結構地震響應模擬精度或導致結構抗倒塌性能分析產生較大誤差，因此，在選擇恢復力模型之后，模型參數的準確度成為影響結構體系模擬精度的主要因素之一.為此，本文提出一種結合擬靜力試驗的混合模擬方法，先從框架結構中選取部分關鍵構件進行擬靜力試驗，然后基于構件實測滯回曲線對構件恢復力模型骨架曲線參數進行識別，最后將識別的參數用于更新結構中相同構件的恢復力模型參數，并進行整體結構非線性數值模擬.在這一混合模擬方法中，模型參數識別是最關鍵的環節之一.

目前在土木工程領域廣泛使用的參數識別方法主要有最小二乘估計法（Least Square Estimation，LSE）、擴展卡爾曼濾波法（Extended Kalman Filter，EKF）和無跡卡爾曼濾波法（Unscented Kalman Filter，UKF）[8]，其中UKF 算法以其高效性成為非線性參數識別的常用方法.但UKF 方法在實際運用時仍存在一些局限性，系統狀態先驗信息矩陣會因為觀測粗差、系統噪聲等不確定的因素失去正定性，中斷濾波進程，觀測粗差等因素還會影響濾波過程，影響收斂速度和識別結果；此外，在UKF 方法中初始協方差矩陣及過程噪聲和測量噪聲矩陣的確定較為繁瑣，但它們的取值卻又決定著參數識別的準確性.基于此，本文運用可抗差的基于奇異值分解的無跡卡爾曼濾波算法（robust unscented Kalman filtering algorithm based on singular value decomposition，抗差SVD-UKF 算法）[9]來解決狀態先驗信息矩陣失去正定性的問題并抑制粗差等對濾波過程的影響，并通過粒子群算法對初始協方差矩陣及過程噪聲矩陣和測量噪聲矩陣進行自動尋優，采用MATLAB 實現了改進IMK 恢復力模型骨架曲線參數的識別.通過基于陸新征等的框架柱擬靜力試驗數據[10]的模型參數識別以及對其整體框架結構擬靜力試驗結果[11]的模擬對比，來驗證本文方法的有效性.

1 改進的IMK 恢復力模型

改進的IMK 恢復力模型是一種用塑性鉸來模擬梁柱構件非線性行為的恢復力模型，它采用三折線骨架曲線（如圖1 所示），其骨架曲線形狀由5 個參數EIy、θcap，pl、θpc、My、Mc/My確定，參數的計算如式（1）～式（5）[12]所示，其循環能量耗散能力λ 的計算如公式（6）所示.

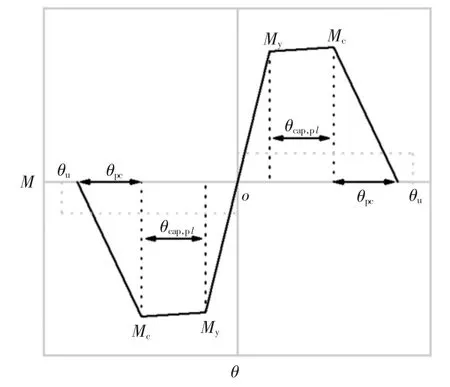
圖1 改進IMK 恢復力模型的骨架曲線Fig.1 Backone curve of the modified IMK hysteretic model

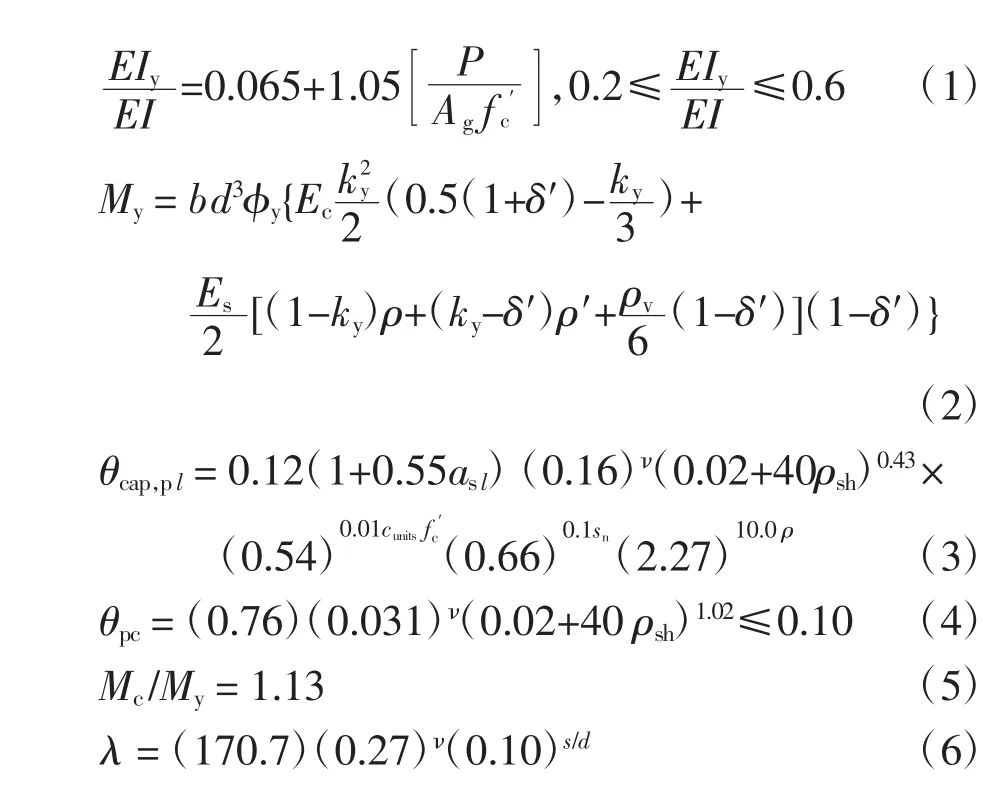
式中：EIy為割線模量；θcap，pl為塑性轉角；θpc為峰值后轉角；My為屈服彎矩值；Mc/My為屈服后硬化剛度；P/Agfc′、ν 均為軸壓比；φy和ky為由構件基本信息計算出的參數，在此不作展開；δ′=d′/d，d′為受壓區邊緣到受壓鋼筋中心的距離；s 為塑性鉸區的箍筋間距；asl為縱向鋼筋滑移系數（考慮取1，不考慮取0）；sn為鋼筋屈曲系數，sn=（s/db）（fy/100）0.5，db為縱筋直徑，fy為縱筋屈服強度；fc′為混凝土軸心抗壓強度，單位為MPa；cunits是單位換算量，當fc′的單位為MPa 時cunits取1；ρsh為柱塑性鉸區的橫向鋼筋面積比；ρ 為縱筋配筋率；b 和d 分別為柱橫截面的寬度和高度.

2 無跡卡爾曼濾波算法

2.1 標準UKF 算法

2.1.1 時間預測

利用第K-1 步狀態向量構造一組總數為2L+1的sigma 點集，L 為狀態量的維度，X 在本文中為待識別的參數K1、K2、K3、fy、fp和恢復力r 組成的狀態向量：

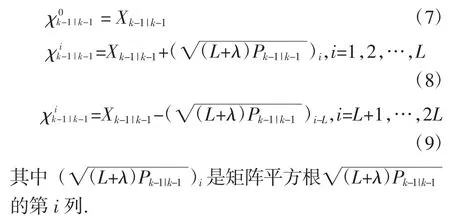
將sigma 點集通過狀態轉移函數映射到新的sigma 點集，本文中狀態轉移函數為通過輸入位移增量及上一時步狀態向量計算得出的下一時步狀態向量：

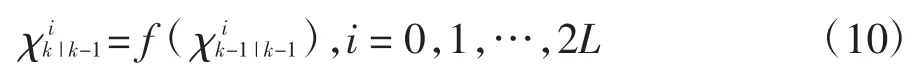
新的sigma 點集用于預測狀態的估計值和協方差：

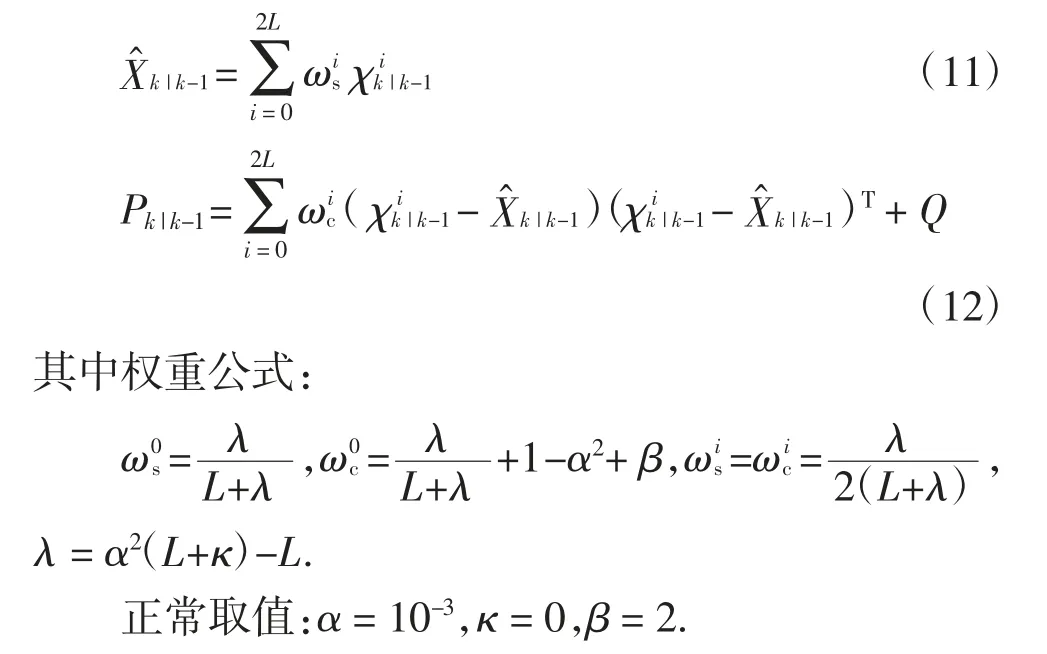
2.1.2 量測更新

構造總數為2L+1 的sigma 點集：

將sigma 點集通過觀測函數映射到新的sigma點集，即恢復力的點集：

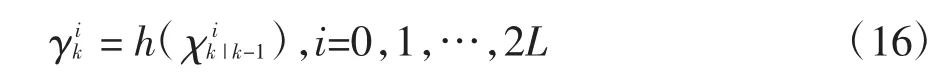
加權新的sigma 點集用于預測觀測的估計值（恢復力值）和協方差矩陣：

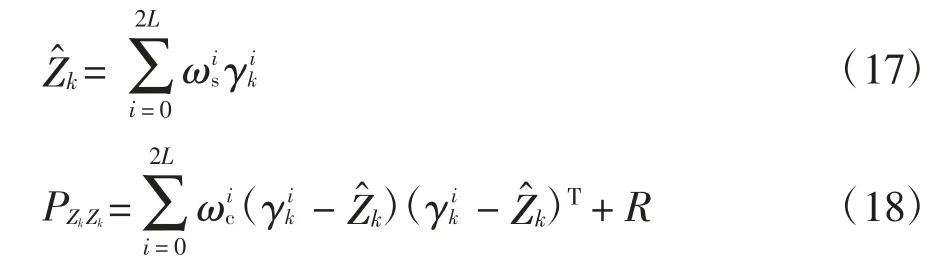
狀態測量的協方差矩陣用于計算卡爾曼增益：

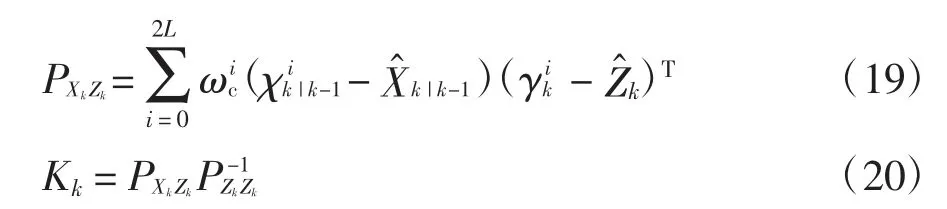
估計更新使用卡爾曼濾波（Kalman Filter，KF）的線性組合思想，得到第K 步的最優估計（K1、K2、K3、fy、fp、r）和協方差矩陣：

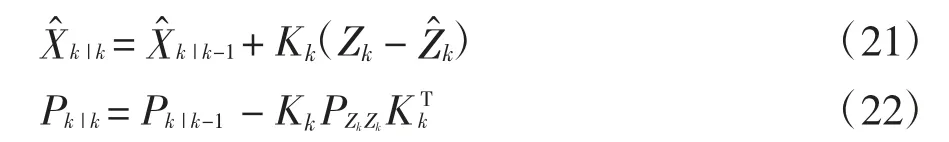
2.2 抗差SVD-UKF 算法

在觀測粗差、計算機截斷誤差等因素的干擾下，狀態協方差矩陣可能會失去正定性，導致無損變換（Unscented Transformation，UT）中的Cholesky 分解失效.本文采用SVD 分解生成sigma 點集，之后在UKF算法中通過抗差因子調節噪聲矩陣來抑制觀測粗差等因素對濾波過程的影響，該算法的流程圖如圖2所示.

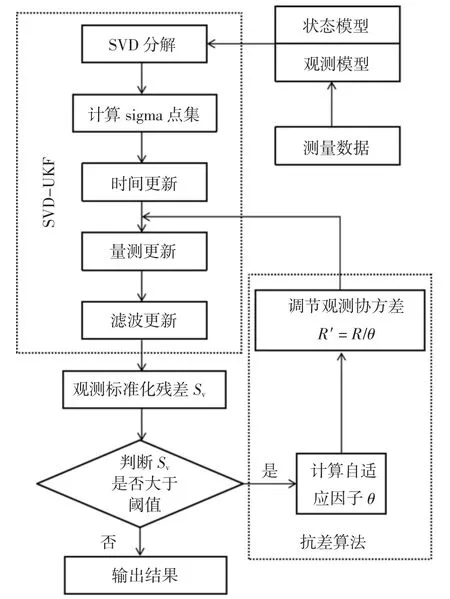
圖2 基于SVD 分解的抗差UKF 算法Fig.2 Robust UKF algorithm based on SVD

2.2.1 抗差模型

抗差因子將觀測值作為考量因素引入濾波過程中，起到動態調整測量噪聲的作用.采用觀測殘差構建抗差因子，抗差因子θk的表達式與IGGIII 函數的形式相似，其表達式如下：

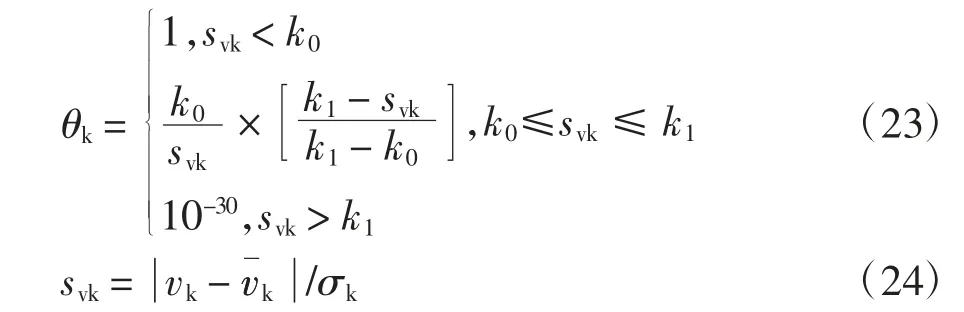
式中：k0、k1為閾值參數，k0通常取1.0～2.0，k1取3.0～8.5，本文中k0取1，k1取3；vk為當前步觀測值與估計值的殘差；為當前步觀測值與估計值殘差的均值；svk、σk分別為當前步觀測值與估計值殘差的標準化量和觀測值與估計值殘差的樣本標準差.

2.2.2 SVD 分解與觀測協方差矩陣的調整

為了解決在異常情況下狀態協方差矩陣失去正定性而無法使用Cholesky 分解的問題，引入SVD 分解計算sigma 點集，計算公式如下：

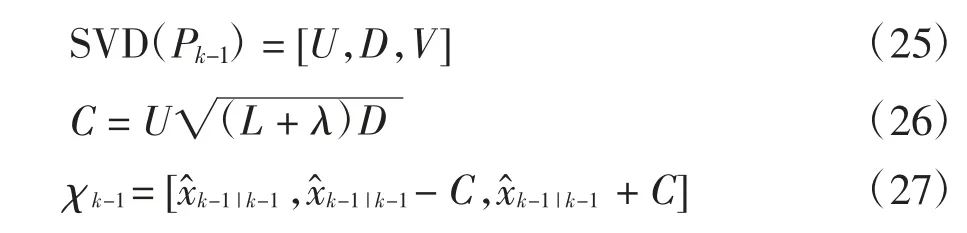
在計算預測觀測協方差矩陣時引入殘差因子，調節測量噪聲來抑制觀測粗差的影響：

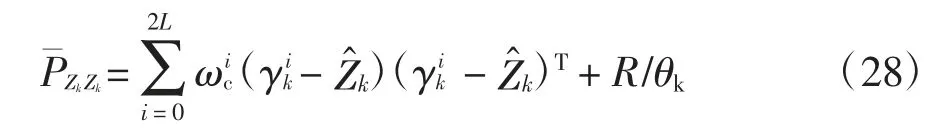
2.2.3 粒子群算法的自動尋優

粒子群算法是模擬鳥群隨機搜尋食物的捕食行為，鳥群通過自身經驗和種群之間的交流調整自己的搜尋路徑，從而找到食物最多的地點，其中每只鳥的位置為自變量組合，每次到達地點的食物密度即為函數值.每次搜尋都會根據自身經驗（自身歷史搜尋的最優地點）和種群交流（種群歷史搜尋的最優地點）調整自身的搜尋方向和速度，這稱為跟蹤極值，從而找到最優解.粒子群算法的流程圖如圖3 所示.

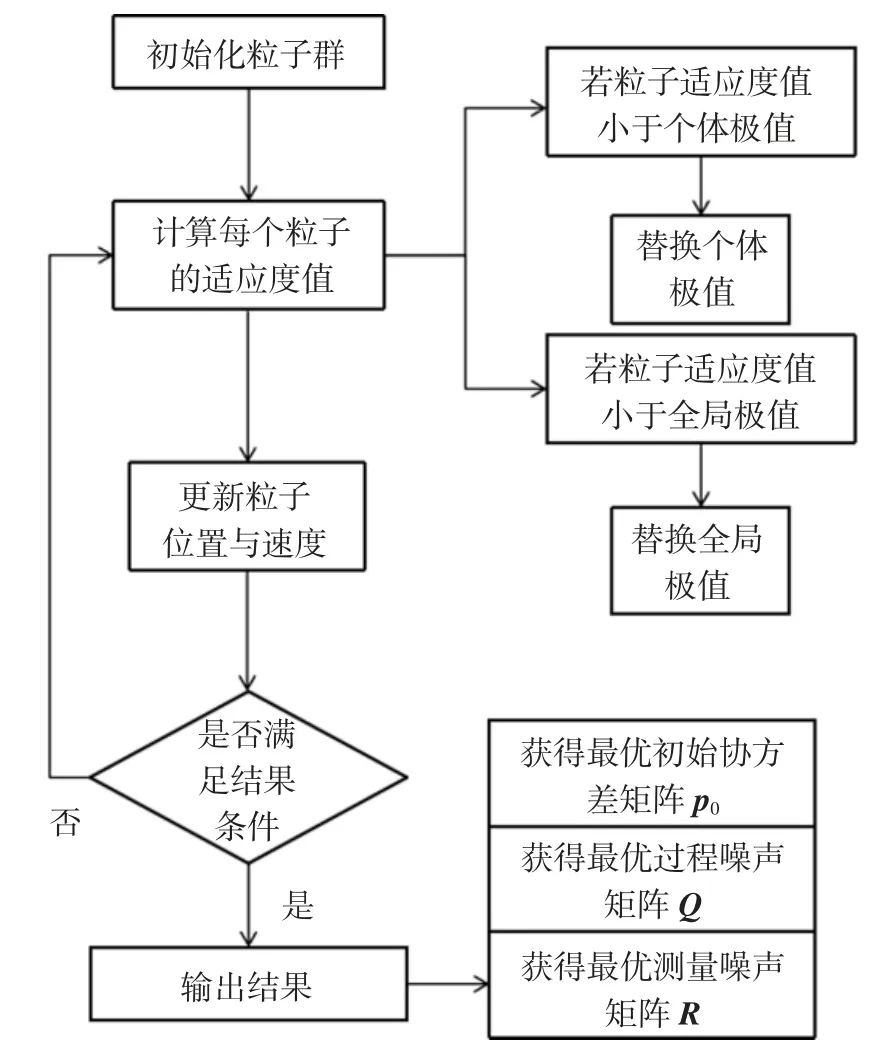
圖3 粒子群算法流程Fig.3 Particle swarm optimization algorithm flow

本文中定義粒子的位置為初始協方差矩陣的每個元素以及過程噪聲和測量噪聲矩陣的每個元素，即相當于構造了一個N 維的空間，并讓鳥群在這個N 維空間中搜尋使適應度函數取值最小的坐標解，適應度函數為在每一個粒子自變量組合經過SVDUKF 算法識別參數后，由識別參數計算所得的每個恢復力值與相應試驗值的殘差平方和，殘差平方和越大表示識別的結果越不可靠，反之則識別結果越可靠，也即粒子自身包含的自變量組合的取值越合理.狀態轉移方程是表示粒子由當前時刻至下一時刻的位置變化方式，狀態轉移方程如下：

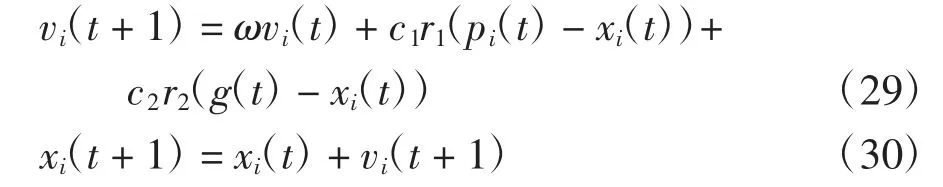
式中：c1、c2均為學習因子；ω 為慣性權重；r1、r2為[0，1]內的隨機常數；pi（t）為個體極值；g（t）為種群極值.

2.2.4 抗差SVD-UKF 算法抗差效果分析

基于改進IMK 三折線模型的MATLAB 仿真，以表1 參數為仿真參數值，通過輸入位移峰值依次為4、10、15、20、25、30、40、45、55 mm 以及各級位移峰值循環兩圈的加載序列，計算得到恢復力序列，之后為檢驗抗差效果將兩類異常觀測引入仿真結果.

1）單點異常：N（0，2Z（i）2）（均值為0，方差為2Z（i）2）的單點隨機誤差，其中Z（i）為當前恢復力值.

2）連續段異常：N（0，2Z（i）2）的連續段隨機誤差.

表1 改進IMK 模型骨架曲線參數仿真值Tab.1 Simulation values of the modified IMK model backone curve parameters

仿真結果加入異常后的觀測值如圖4 所示，之后分別采用未抗差的UKF 算法及抗差的SVD-UKF算法對加入異常的觀測恢復力值進行濾波，濾波過程如圖5 所示.

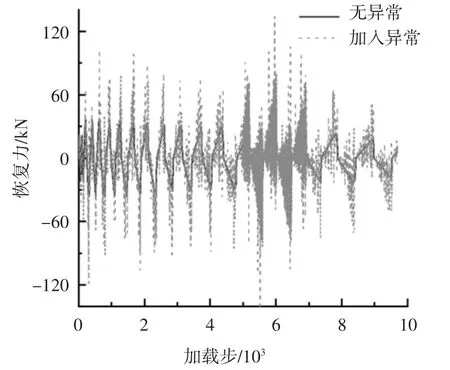
圖4 仿真結果加入異常后的觀測值Fig.4 Observations after adding anomalies

圖6 為在引入單點異常后截取的2 000～4 000加載步的濾波過程圖.由圖6 可見，抗差算法的濾波過程跟真實值基本吻合，而未抗差算法的濾波過程受到單點異常影響而出現了偏離.

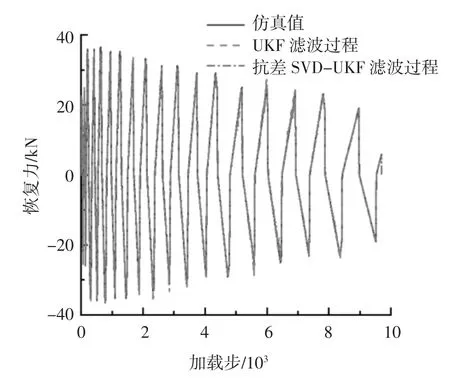
圖5 兩種算法對異常觀測值的濾波過程Fig.5 Filtering process of abnormal observations by two algorithms

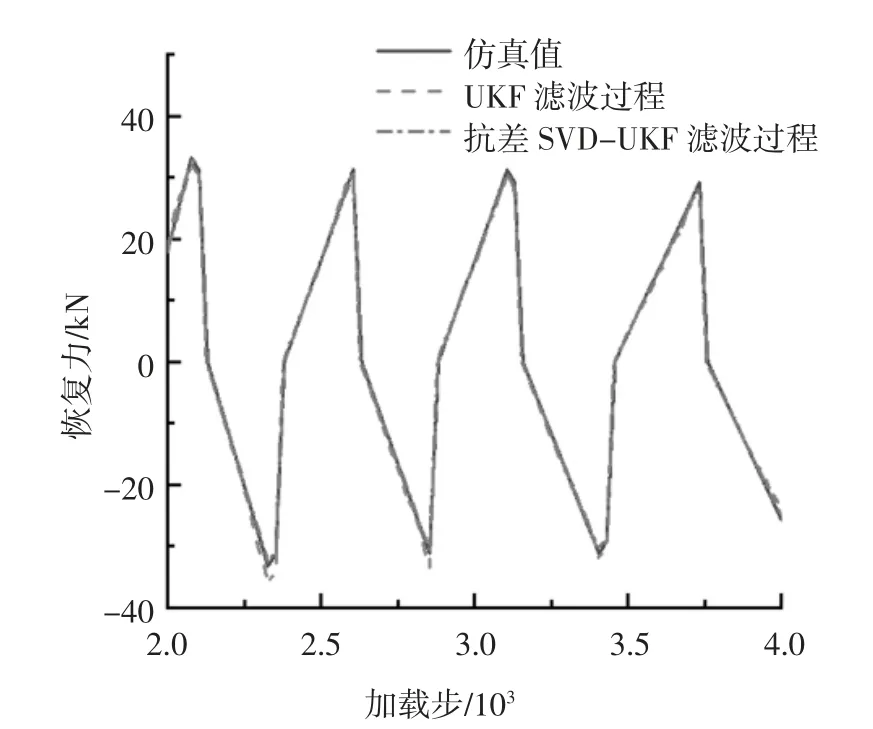
圖6 濾波過程的2 000～4 000 加載步恢復力時程對比Fig.6 Comparison of restoring force time history of 2 000 to 4 000 loading steps in the filtering process

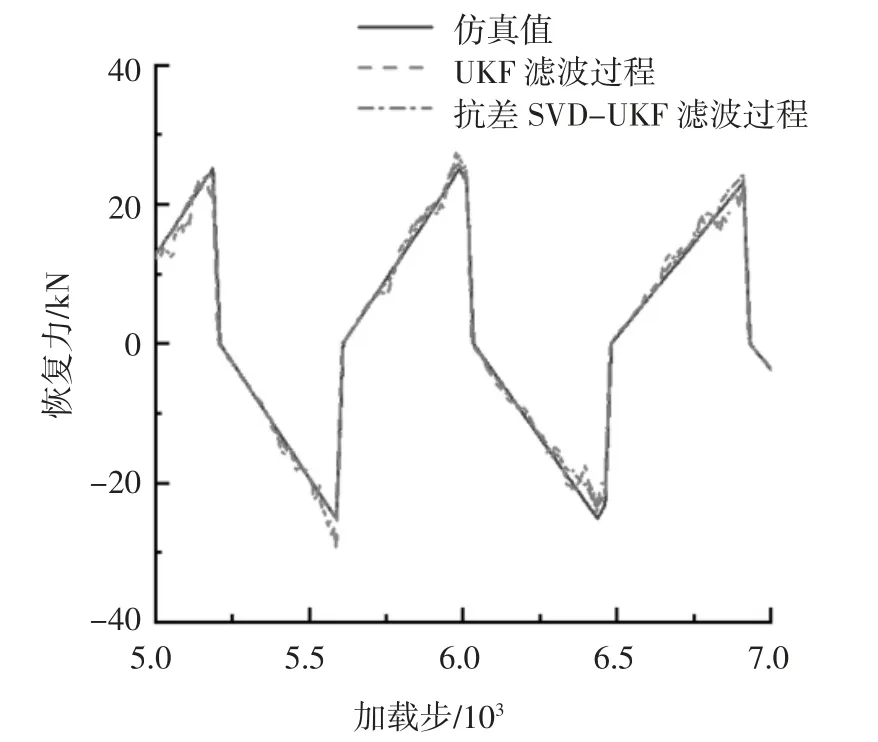
圖7 濾波過程的5 000～7 000 加載步恢復力時程的對比Fig.7 Comparison of restoring force time history of 5 000 to 7 000 loading steps in the filtering process

圖7 為在5 000～7 000 加載步引入連續段隨機誤差后截取的5 000～7 000 加載步的濾波過程圖.由圖7 可知，抗差算法的濾波過程跟真實值基本吻合，而未抗差算法的濾波過程受到了連續段異常的影響而出現了較大波動.

可見，在兩種異常的影響下抗差SVD-UKF 算法擁有較強的魯棒性與吻合程度.

3 低周反復荷載下鋼筋混凝土柱的骨架曲線參數識別

3.1 試驗概況

本文試驗實測數據采自陸新征等[10-11]鋼筋混凝土框架結構擬靜力倒塌試驗研究，試驗包括一榀3層3 跨整體框架的擬靜力試驗和一些關鍵構件的擬靜力試驗.關鍵構件包括底層邊柱和中柱各兩個試件，層一的邊節點和中節點各一個試件，本節參數識別選用了其中邊柱A 和中柱C 的試驗數據.邊柱A和中柱C 的幾何尺寸和配筋如圖8 所示，其中中柱角筋直徑為10 mm，鋼筋材料參數如表2 所示，混凝土強度和對柱子施加的軸力如表3 所示.柱子擬靜力試驗的加載路徑如下.

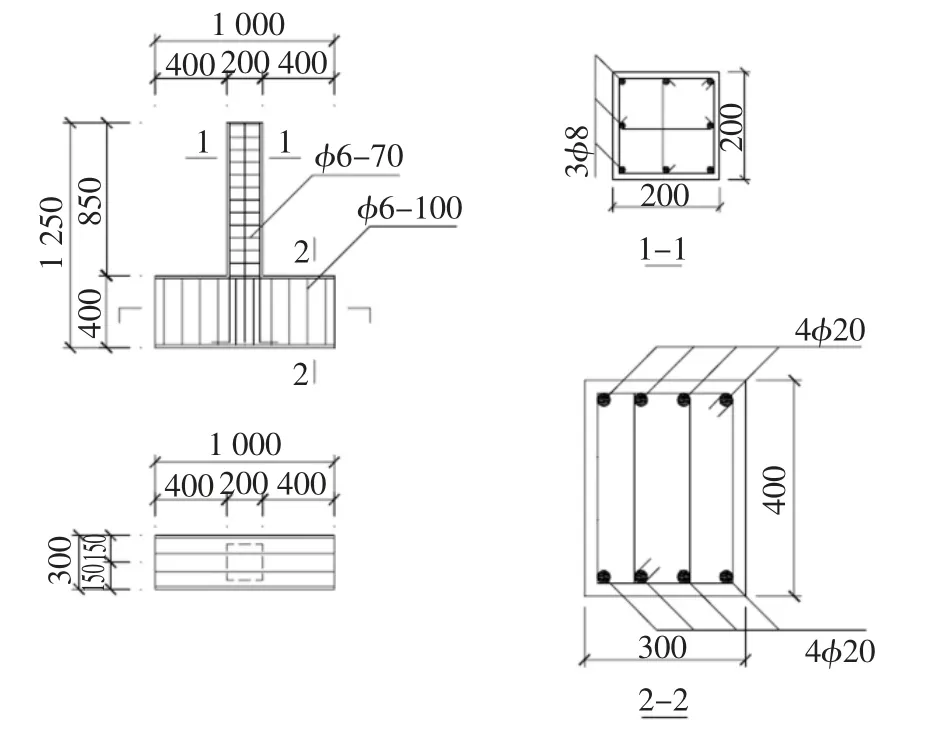
圖8 柱的尺寸配筋圖Fig.8 Column dimensions and reinforcement detailing

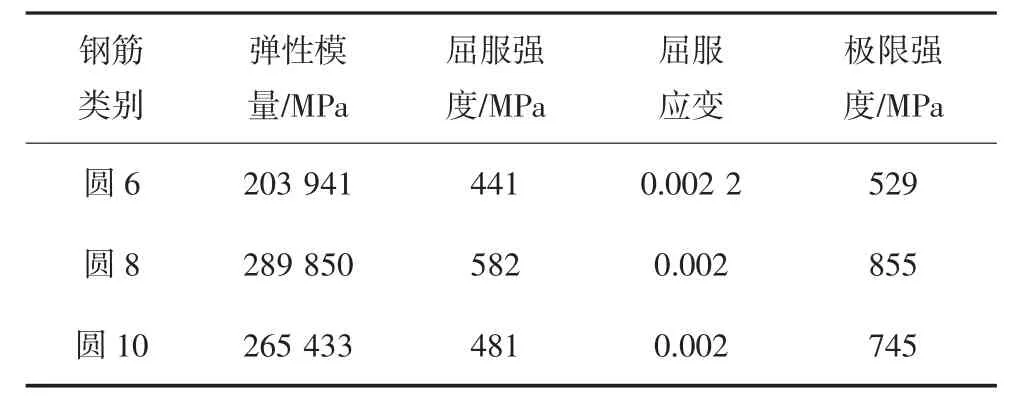
表2 鋼筋材料參數Tab.2 Material parameters of rebar

表3 混凝土強度和豎向軸力Tab.3 Concrete strength and axial force

邊柱A 試驗中首先施加柱端豎向荷載至試驗軸壓比，然后以水平荷載控制加載10 kN/級至30 kN，各級荷載循環一圈.此后以水平加載點位移控制加載，所加水平位移峰值分別為10、15、20、25、30、37.5、45、55 mm，各級位移循環兩圈.

中柱C 試驗中首先施加柱端豎向荷載至試驗軸壓比，之后以水平荷載控制加載10 kN/級至40 kN，各級荷載循環一圈.此后以水平加載點位移控制加載，所加水平位移峰值依次為10、15、20、25、30、37.5、45、55 mm，各級位移循環兩圈.

3.2 基于柱試驗結果的改進IMK 對稱模型參數識別

本文采用抗差SVD-UKF 算法，在MATLAB 中編寫了識別改進IMK 對稱模型骨架曲線參數的程序，識別參數包括彈性剛度K1、硬化剛度K2、退化剛度K3、屈服力fy和極限力fp這5 個參數.在后續的滯回曲線對比中，試驗結果為柱子擬靜力試驗的實測滯回曲線；初始結果是指通過公式（1）～（6）計算得出改進IMK 模型參數值后，依據柱子的位移加載路徑計算得到的滯回曲線；以初始結果中計算得到的模型參數為參數識別的初始值，識別出5 個待識別參數后，依據柱子的位移加載路徑計算得到的滯回曲線稱為識別結果.

邊柱A 的改進IMK 模型骨架曲線參數的初始值和識別值對比如表4 所示.用初始值和識別值分別計算出柱子的滯回曲線，邊柱A 計算滯回曲線和試驗滯回曲線的對比分別如圖9 和圖10 所示，與初始結果相比，識別結果與試驗結果吻合較好，也即通過參數識別提高了模型參數的準確度.

表4 邊柱A 的改進IMK 模型骨架曲線參數初始值和識別值對比Tab.4 Initial and identified values of backone curve parameters of the modified IMK model of side column A

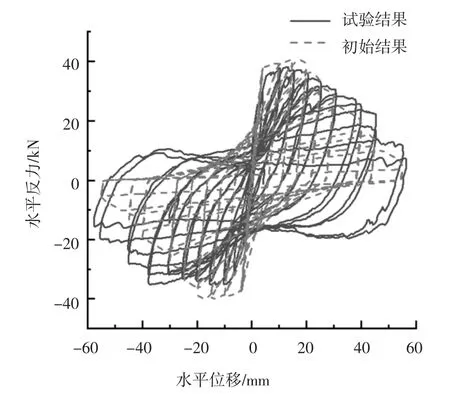
圖9 邊柱A 滯回曲線試驗結果與初始結果對比Fig.9 Comparison of test and initial hysteresis of side column A

圖10 邊柱A 滯回曲線試驗結果與識別結果對比Fig.10 Comparison of test and identified hysteresis of side column A

圖11 為邊柱A 的試驗結果、識別結果和初始結果的滯回環面積對比.由圖11 的滯回環面積數據計算得到邊柱A 的識別結果滯回環總面積與試驗結果滯回環總面積相差8.15%，邊柱A 初始結果滯回環總面積與試驗結果滯回環總面積相差15.77%.從滯回環總面積差來看，與初始參數相比，采用識別參數可以更好地模擬柱構件的滯回曲線.

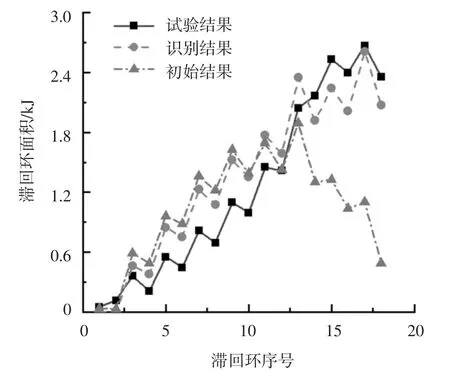
圖11 邊柱A 的滯回環面積對比Fig.11 Comparison of hysteresis loop area of side column A

3.3 基于柱試驗結果的改進IMK 非對稱模型參數識別

在上述識別方法中，通過修改MATLAB 中的程序，實現了改進IMK 非對稱模型骨架曲線參數的識別.

中柱C 的改進IMK 模型骨架曲線參數初始值和識別值對比如表5 所示.用初始值和識別值分別計算出柱子的滯回曲線，計算滯回曲線和試驗滯回曲線的對比分別如圖12 和圖13 所示.與初始結果相比，識別結果與試驗結果吻合較好，也即通過參數識別提高了模型參數的準確度.

圖14 為中柱C 試驗結果、識別結果和初始結果的滯回環面積對比.由圖14 的滯回環面積數據計算得到識別結果滯回環總面積與試驗結果滯回環總面積相差26.03%，初始結果滯回環總面積與試驗結果滯回環總面積相差31.79%.可見，與初始參數相比，采用識別參數可更好地模擬柱構件的滯回曲線.

表5 中柱C 的改進IMK 模型骨架曲線參數初始值和識別值對比Tab.5 Initial and identified values of backone curve parameters of the modified IMK model of middle column C

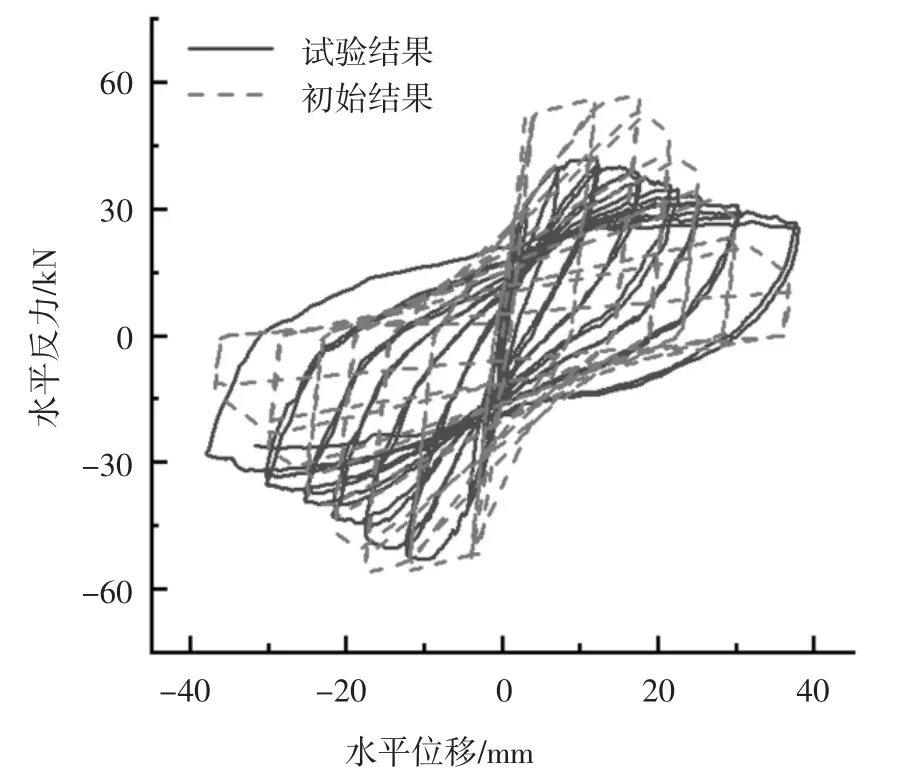
圖12 中柱C 滯回曲線試驗結果與初始結果對比Fig.12 Comparison of test and initial hysteresis of middle column C

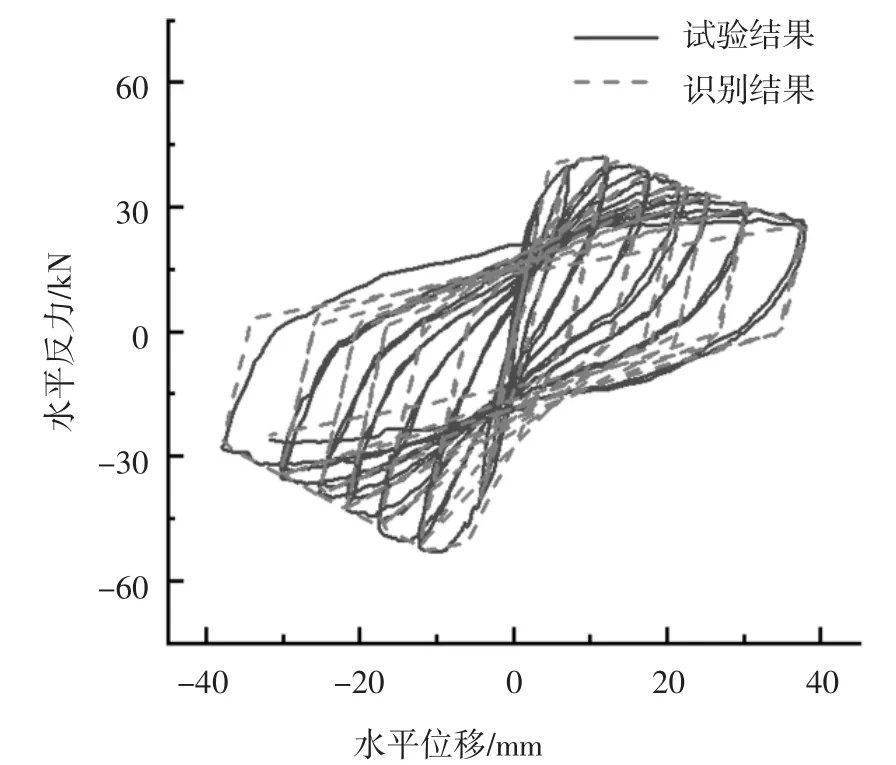
圖13 中柱C 滯回曲線試驗結果與識別結果對比Fig.13 Comparison of test and identified hysteresis of middle column C

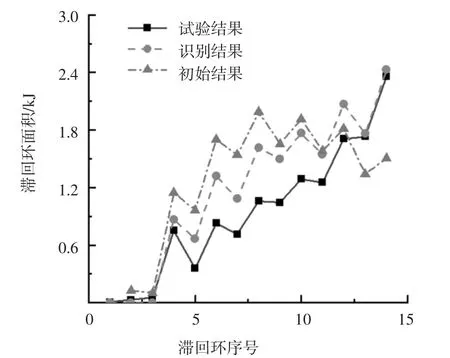
圖14 中柱C 滯回環面積對比Fig.14 Comparison of hysteresis loop area of middle column C

4 基于柱構件參數識別結果的應用

為檢驗基于柱實測滯回曲線的模型骨架曲線參數識別值的有效性，以下將識別的模型參數應用于整體框架結構的數值模擬，所選的框架結構來自陸新征等[10-11]完成的一榀3 層3 跨鋼筋混凝土框架結構擬靜力倒塌試驗.整體框架的數值模擬采用OpenSees 建模，建模流程如下.

首先計算得到改進IMK 模型的輸入參數，然后在OpenSees 中調用改進IMK 模型并定義塑性鉸材料，最后將材料用于梁柱端部零長度單元的彎曲特性，其余單元均為彈性梁柱單元.柱端部改進IMK 模型參數按兩種工況取值換算，工況1 采用由柱端截面的尺寸、材料、配筋、軸力等參數按照公式（1）～（6）計算得到的模型參數值；工況2 采用基于柱實測試驗數據得到的參數識別值，其中中柱的參數值選用中柱C 負向的參數識別值，將參數識別值換算成模型參數值后，對割線剛度EIy、塑性轉角θcap，pl和峰值后轉角θpc根據框架的實際軸力按照公式（1）（3）（4）中軸壓比的分項作了調整，考慮到屈服彎矩與軸壓比關系的復雜性，對屈服彎矩My和屈服后硬化剛度Mc/My分別按公式（2）和公式（5）計算取值，對λ 取一較大值，即不考慮構件的循環能量耗散.之后，根據擬靜力試驗設定的加載路徑，進行了兩種工況下框架結構的數值模擬.圖15 為兩種工況下基底剪力-頂點位移數值模擬滯回曲線和試驗滯回曲線的對比.圖16 為工況1、工況2 與試驗結果的滯回環面積對比.

從圖15 曲線對比可以看出，工況1 與工況2 均對試驗情況作出了較好的模擬.由圖16 的滯回環面積數據計算得到基底剪力-頂點位移識別結果的滯回環總面積與試驗結果的滯回環總面積相差23.71%，初始結果滯回環總面積與試驗結果滯回環總面積相差36.50%.從滯回環總面積差來看，與初始參數相比，采用識別參數可以更好地模擬框架結構的整體響應.

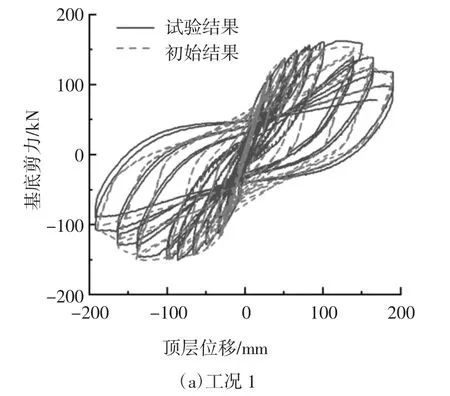
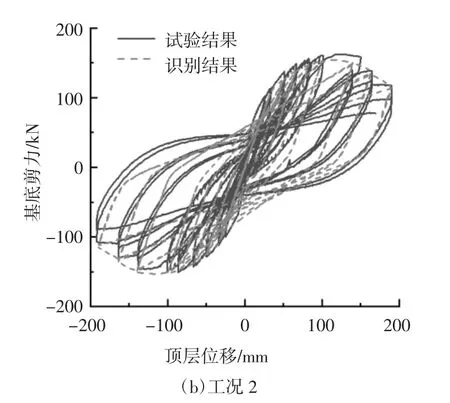
圖15 基底剪力-頂點位移滯回曲線Fig.15 Base shear-top displacement hysteresis

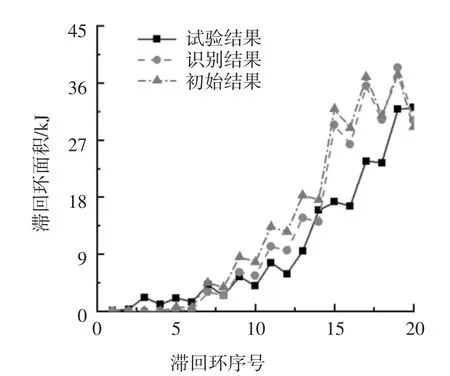
圖16 基底剪力-頂點位移滯回環面積對比Fig.16 Comparison of base shear-top displacement hysteresis loop area

5 結論

1）將抗差SVD-UKF 算法運用于鋼筋混凝土柱改進IMK 模型的參數識別，有效抑制了觀測粗差對識別進程的影響，并通過粒子群算法對初始協方差矩陣、過程噪聲矩陣、測量噪聲矩陣進行自動尋優，省去了大量的人力調參工作.

2）基于陸新征等[10-11]鋼筋混凝土框架柱構件擬靜力試驗實測滯回曲線數據，對柱子的改進IMK 模型骨架曲線參數進行了識別，結果表明識別參數精度較初始參數精度有明顯提高.

3）將基于柱子試驗數據識別的骨架曲線參數用于框架結構的擬靜力加載試驗數值模擬，結果表明利用識別參數可提高整體結構的數值模擬精度.