潛堤上規則波輻射應力的數值研究

穆浩然馬小舟毛艷軍高 翔

(1.大連理工大學 建設工程學部,遼寧 大連116024;2.海岸和近海工程國家重點實驗室,遼寧 大連116024)

輻射應力概念最初是由Longuest-Higgins和Stewart[1]提出并給出了適用于計算微幅波輻射應力值的簡化公式。在近岸波浪的傳播運動中,由于海水深度變淺導致了波浪產生嚴重變形甚至破碎,從而引起輻射應力的強烈改變,輻射應力變化對沿岸波生流、波浪增水(set-up)、波浪減水(set-down)有著重要影響,也是低頻波浪生成的重要驅動力。Longuest-Higgins和Stewart[2]認為波浪輻射應力的增加將促使波群中自由長波的釋放;Symonds等[3]建立了控制方程中含有輻射應力受迫項的碎波拍模型,認為波群中波浪破碎點前后移動引起輻射應力在時間及空間上的改變產生了低頻波浪;Kostense[4]定性地驗證了短波群波浪破碎點移動導致低頻波浪產生的理論。因此,為了更加準確地了解輻射應力這一波浪特性,眾多學者通過理論分析,數值和實驗模擬的手段進行輻射應力的計算。對于常水深Graham[5]提出用有限差分法計算輻射應力張量;鄭金海和嚴以新[6]利用線性波理論研究波浪輻射應力張量隨深度變化的分布規律,并給出適用于任意波向角的輻射應力的表達式;Xia等[7]提出了輻射應力垂向剖面的定義和計算公式,并利用斜坡上波生流的實驗結果證明了模型的準確性;Stive和Wind[8]利用實驗數據,通過線性外推法近似求得湍流波浪速度剖面來計算輻射應力沿程變化;溫秀媛等[9]利用改進色散關系的Boussinesq方程推導出了全新的輻射應力計算公式,探究輻射應力對波浪增減水的影響。然而,上述輻射應力計算方法都難以獲得碎浪帶內詳細的流場信息,并存在著一定程度的條件假設和公式簡化,因此計算所得輻射應力結果誤差較大。

基于OpenFOAM[10]軟件開源程序建立數值水槽則是模擬波浪破碎區流場信息的一個較為可行的手段,可以詳細研究完整計算域內波浪輻射應力隨波浪傳播而產生的變化過程。查晶晶和萬德成[11]基于OpenFOAM軟件進行的數值造波實驗驗證了此數值方法造波和消波方式的可靠性;王東旭等[12]利用此軟件較好地模擬了孤立波在潛礁上的波浪破碎及水躍現象;毛艷軍等[13]應用Open FOAM軟件求解了箱式浮式防波堤的水動力性能,并分析了其作為垂蕩浮子式波能轉換裝置的能量轉換性能;姚宇等[14]運用Open-FOAM軟件模擬孤立波在島礁地形的傳播,數值輸出的破碎區內波形及流速與實驗結果對比良好;張陳浩和鄭茜[15]利用OpenFOAM軟件模擬規則波在淺灘上的破碎變形,模擬結果與實驗結果相吻合,且輸出了能較好體現波浪破碎整體過程的流場信息。

本文擬應用OpenFOAM軟件來模擬波浪在潛堤地形下的傳播破碎,在進行平底水槽線性波的數值模擬和數值模型模擬波浪的準確性及計算輻射應力方法的有效性驗證后,進行規則波在潛堤地形下傳播破碎的模擬研究,在此基礎上對輻射應力沿程變化的特點及其對波浪增減水的影響開展了研究,并探討了平底地形下輻射應力與波幅偏移量之間的關系。

1 理論基礎

1.1 控制方程

本文采用基于Open FOAM軟件的造波模塊waves2Foam[16]開展波浪傳播變形的數值模擬。坐標系統為笛卡爾坐標系,x方向為波浪的入射方向,y方向為垂向,z方向為沿水槽的寬度方向,基于不可壓縮流體的運動特點,控制方程為:

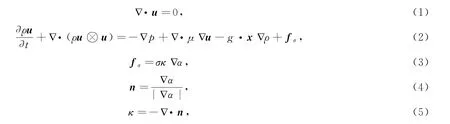
式(1)～式(5)中,ρ為混合流體的密度;u為流體的速度場;t為時間;μ為動力黏性系數;g為重力加速度;x為位置矢量;fσ為自由表面的張力;σ為張力系數;κ為自由表面的平均曲率;n為界面單位法向量;α為流體體積分數。

對于自由表面的處理,根據VOF法將2種流體看作一種混合流體,實現每個單元相界面的追蹤,引入相函數:

在求解時,式(2)中的混合流體的密度ρ可用液體密度ρ1和氣體密度ρ2表示,動力黏性系數μ可用液體黏性系數μ1和氣體黏性系數μ2來表示:

同時,α滿足輸運方程:

傳統的VOF法需要反復地進行自由表面的重構,降低了計算效率,因此Weller[17]引入了額外的人工壓縮項來實現對自由水面的精確捕捉,式(9)可變為

式中:uc為適用于壓縮自由面及調整自由面尖銳程度的速度場,新增加的人工壓縮項只對界面過渡區起作用,不會影響到周圍流場。

1.2 輻射應力公式

將作用于單位面積水柱體的總動量流的時均值減去沒有波浪作用時的靜水壓力定義為波浪輻射應力。Longest-Higgins和Stewart[18]給出的水平x方向輻射應力(S xx)的定義公式為

式中:u為質點速度在x方向的分量;h為水深;η為水面高程;i為平均水面高程;p為總壓。

對于微幅波,輻射應力計算公式可簡化為

2 模型驗證

2.1 波形驗證

表1 不同工況下的網格尺寸Table 1 Sensitivity analysis of grid size

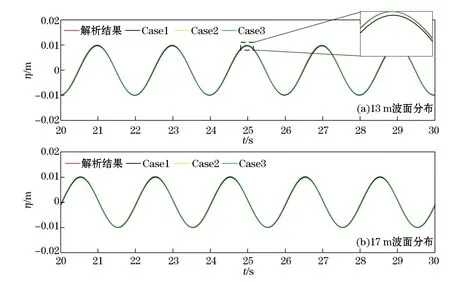
圖1 不同網格尺寸下波面變化與解析波面對比Fig.1 Comparison diagram of wave surface between experimental results and numerical simulation with different grid size

將模型作用于模擬平底水槽中線性波的傳播,其模擬工況為:波高0.02 m,波周期2 s,水深1 m,計算域長30 m,高1.1 m,數值水槽前端和后端各設置6 m松弛區(消波),模擬計算時長30 s,采用自動調整計算時間步長的方法,設置輸出時間步長Δt=0.02 s。模型應用Case1,Case2和Case3三種不同大小的網格設置來進行敏感性分析,具體網格尺寸見表1。不同網格尺寸下波面對比如圖1所示,由圖可見,Case1網格尺度下模擬的波浪波峰值明顯低于解析結果,由此產生的誤差將影響到之后的數值計算,而Case2和Case3網格尺度下模擬的波浪則與理論解對應很好。因此,為保證波浪輻射應力計算結果的準確性并且能夠節約計算資源,本文采用Case2網格尺寸進行模擬計算。得到了較好的數值模擬結果,其波面與理論波面的運動趨勢及波峰波谷值均吻合較好,誤差較小,由此說明本文所用數值模型可以很好地模擬波浪運動。

2.2 輻射應力計算結果驗證

將上述工況中數值模擬計算的輻射應力沿程變化結果與微幅波理論下輻射應力結果進行比對,對比結果如圖2所示。由式12和式13計算得到微輻波理論下的輻射應力值為0.4709 N/m,數值模擬結果中輻射應力值有較小幅度的振蕩,可能是由波浪沿水槽傳播過程中波幅產生微小差異所致,但整體而言,本模型模擬結果與理論結果對應得較好,說明本數值模型模擬波浪運動輸出的流場、壓力場較準確,輻射應力計算方法也是可行的。

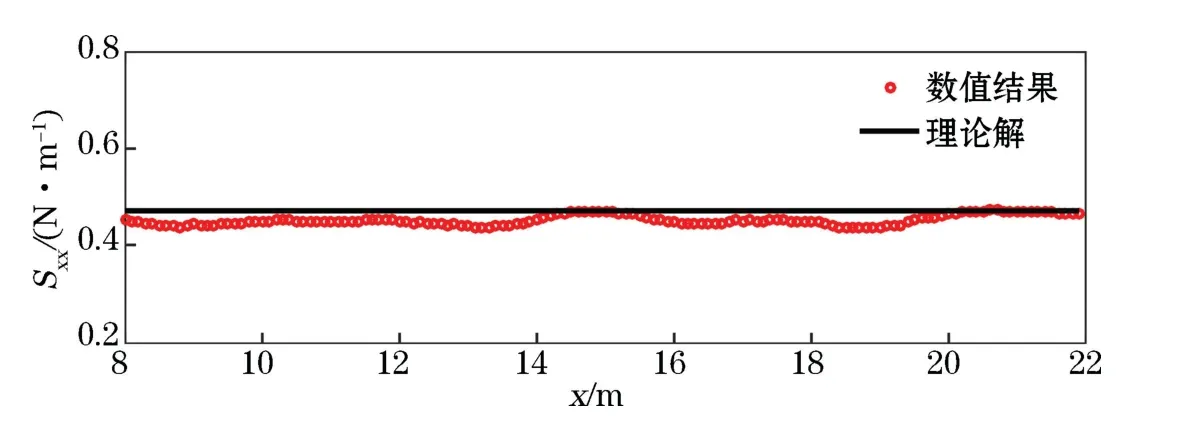
圖2 平底水槽中數值模擬輻射應力值及微輻波理論輻射應力結果對比Fig.2 Comparison of numerical simulation and airy wavetheory results of radiation stress at flat tank

3 潛堤地形下輻射應力計算及波浪增減水模擬

潛堤地形的實驗案例采用Beji和Battjes[19]的實驗地形及工況,數值模擬Case A和CaseB兩種工況下波浪的傳播,并計算輻射應力及波浪增減水的沿程變化情況。本文采用層流模型來進行數值計算,利用相對較小的網格尺度進行波浪破碎的求解,能夠得到較好的波浪模擬結果,且與湍流模型RANS相比,層流模型計算所得的破波區內波浪運動與實際波浪運動更為相似,能更好地模擬出波浪的破碎形態和波浪破碎后波面的起伏振蕩現象,由于篇幅有限,在此不作更多的說明。數值模型布置如圖3所示,堤頂高度為0.3 m,波浪沿水槽正向傳播。數值模擬計算域長40.0 m,前后各設置8.0 m松弛區,計算時長為50 s,CaseA,CaseB均采用自動調整計算時間步長的方法,輸出時間步長分別為Δt=0.02 s,Δt=0.025 s。總網格量均為80萬,x方向網格尺寸為0.01 m,y方向網格尺寸為0.0025 m。數值模擬實驗工況如表2所示。

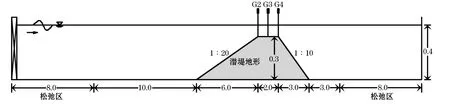
圖3 潛堤地形布置(m)Fig.3 Layout of the submerged bars(m)

表2 潛堤地形實驗工況列表Table 2 List of experimental cases of submerged bars topography

3.1 波形對比

當波浪傳播到潛堤前坡坡頂位置時,非線性效應達到最大,波浪發生明顯的破碎。將堤頂G2,G3和G4三處波面的時間變化曲線與實驗結果對比,結果見圖4,可以看出,在波浪初破階段,Case A和CaseB工況的G2,G3處數模波峰波谷值與實驗結果對應較好;在波浪完全破碎后(G4),2個工況的數值模擬計算結果均出現了低估峰值和谷值的現象。但是數值模擬的兩工況的整體運動趨勢,特別是破碎后波浪振蕩趨勢與實驗現象基本一致,說明該數值模型可以較好地反映實驗中波浪破碎后的實際運動,模擬的波浪破碎具有較大的可信度。圖5給出了潛堤堤頂位置(24～26 m處)波浪破碎時的流場信息,可以清楚地看到,當破碎發生時,破碎點周圍水質點的速度方向均指向破碎點處,越靠近破碎點的水質點速度值越大,在破碎波面處水質點運動最為劇烈,速度值達到最大。而距離破碎點較遠的流場中,水質點速度較小,水體流動較為溫和,但是受前一破碎波浪的影響,水體中水質點移動較為混亂,方向具有不確定性,這與波浪運動的實際情況較為符合,因此本數值方法計算所得流場信息較為可信。

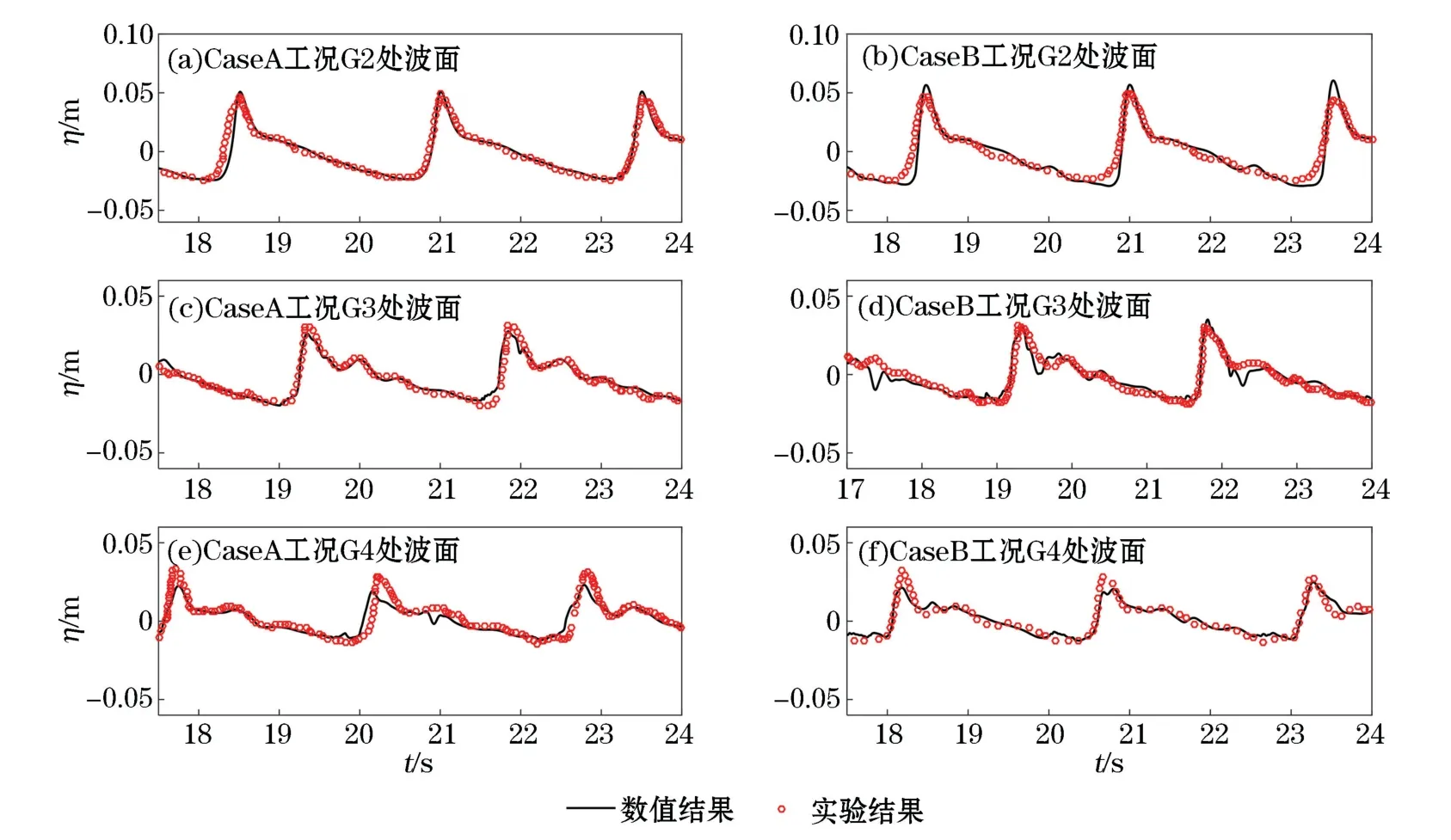
圖4 CaseA和CaseB兩種工況下G2、G3、G4處波面對比Fig.4 Comparison of wave surface at G2,G3 and G4 under CaseA and CaseB

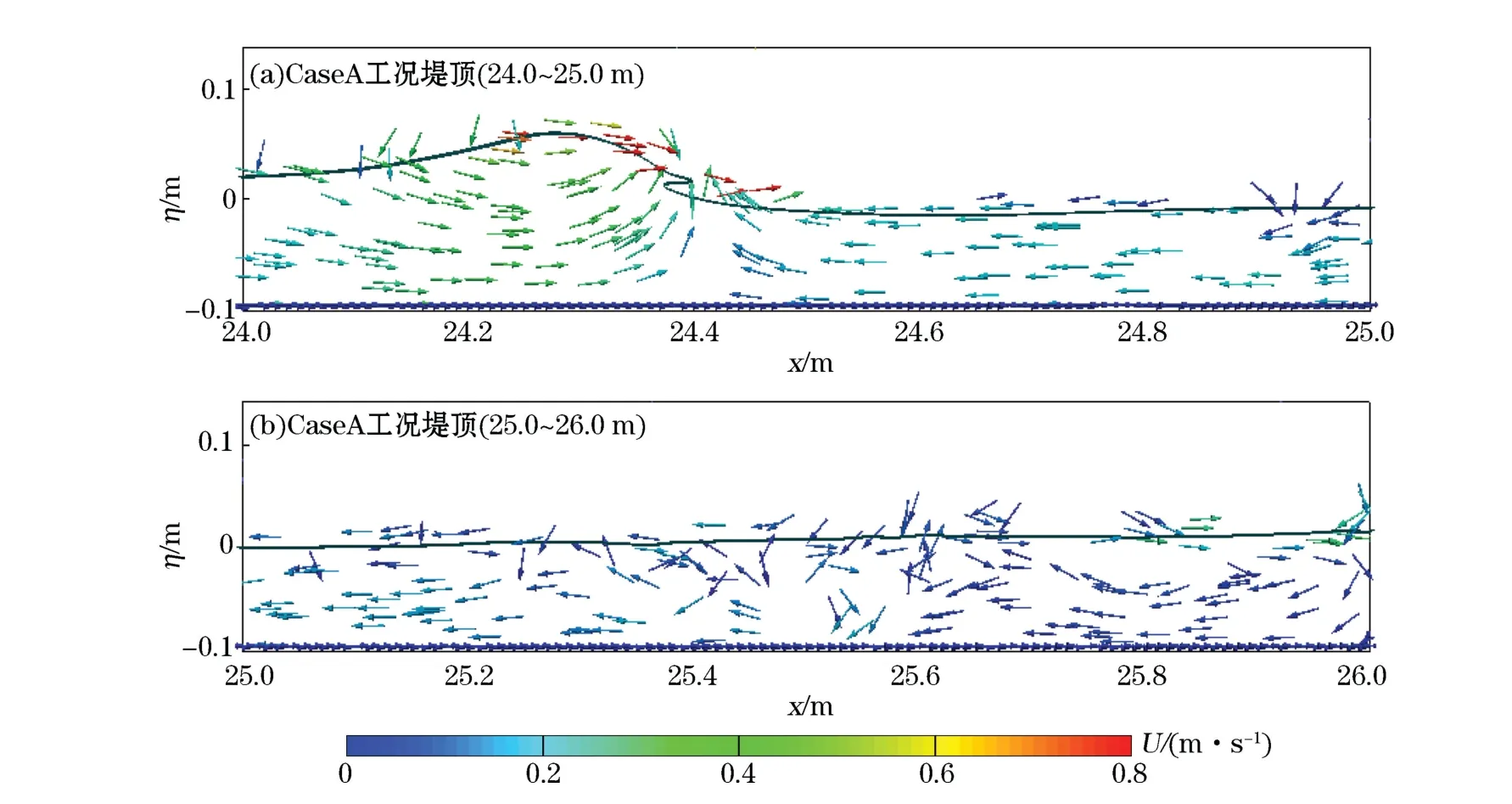
圖5 Case A工況堤頂位置流場分布Fig.5 The flow field distribution at the top of the dam under Case A

3.2 輻射應力與波浪增減水

當波浪傳播到潛堤區域時,會發生淺水變形并最終產生破碎,繼而波高驟降,波浪動量減小,輻射應力將沿程發生變化,進而影響平均水平面的改變,這一波浪平均水平面的變化便稱為波浪的增減水。當規則波沿x方向正向入射時,依據波浪增減水方程可知:

當輻射應力(S xx)沿程增長,即時,則波浪將產生減水現象;當輻射應力沿程降低,即時,則波浪將產生增水現象。波浪增減水的值即為波面升高的時均值與靜水面位置的差值。本文根據數值模型輸出的波面數據,進行周期內時間平均,得到Case A和CaseB兩個工況下的波浪增減水變化。

圖6和圖7給出了潛堤地形下2種工況的波浪輻射應力和波浪增減水的沿程變化曲線。2個工況均能明顯看出,當波浪傳播在堤前平底時,輻射應力基本呈穩定值,到潛堤前坡坡底附近其值開始增大,直至堤頂處達到最大值,隨后產生下降的趨勢,在潛堤后坡面處由于水深的增加,輻射應力值再次增大,直至堤后平底水槽處趨于平穩。而波浪增減水的沿程變化趨勢恰好與之相反。由于波浪完全破碎,波浪成分不穩定,在堤后坡面至平底處的輻射應力和平均水平面均有明顯震蕩,但是整體變化趨勢依舊能較好地滿足波浪增減水方程。

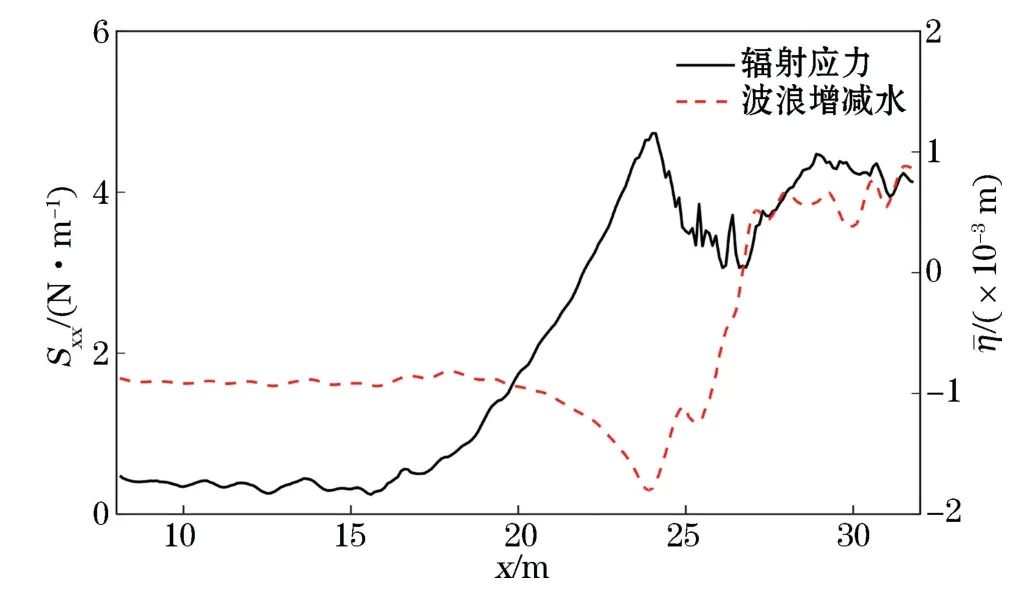
圖6 CaseA波浪輻射應力與增減水沿程變化情況Fig.6 Variation of wave radiation stress and wave set-up,wave set-down under Case A

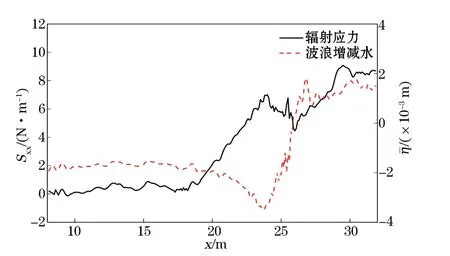
圖7 CaseB波浪輻射應力與增減水沿程變化情況Fig.7 Variation of wave radiation stress and wave set-up,wave set-down under CaseB

另外,在堤前平底處,模型穩定后的輻射應力結果較小,這是由于隨著波浪的傳播,堤前反射波使波幅隨著時間推移產生下沉現象,從而導致輻射應力定義公式中的速度積分項和動壓積分項變小,最終導致了輻射應力結果偏低。由圖8可見,Case A工況下15 m水槽處波面過程曲線及波幅偏移值隨時間變化的曲線,將波幅偏移值量化為波浪上下幅值之和,并將其進行無量綱化,其中au表示波浪的上幅值,ad表示波浪的下幅值。波幅的偏移值在30 s后基本達到穩定狀態,同時由圖9可見數值水槽前端平底15 m處不同周期內的波幅偏移值與其對應的輻射應力值關系,較明顯地反映出潛堤工況下的平底水槽部分輻射應力結果與對應周期內波浪幅值的偏移值成正相關,且受波幅變動影響較為敏感,波幅偏移值越小,輻射應力值越低。結合圖8和圖9來看,圖8中當波浪波幅偏移值達到穩定狀態時,其值對應于圖9中輻射應力值大概為0.5 N/m處的點,較理論預估值低,而波浪傳播初期的波浪偏移值對應的同周期內的輻射應力結果約為3 N/m,這與理論預估值基本一致,由此可見平底水槽處波浪穩定時輻射應力結果偏低是波幅偏移值變小造成的。而造成波浪波幅產生振蕩的原因還需進一步地分析探討。

圖8 CaseA工況中水槽15 m處波面變化及波幅偏移量變化Fig.8 Wave surface change and amplitude offset change at 15 m on the tank under Case A

圖9 CaseA工況水槽15 m處不同周期內波浪波幅偏移量與其對應輻射應力值關系Fig.9 The relation figure between wave amplitude offset and corresponding value of radiation stress at 15 m of tank under CaseA

4 結 語

本文應用Open FOAM數值模型模擬有破碎情況下潛堤地形的波浪傳播,詳細地輸出了碎浪區波浪運動的流場信息,完整地計算了波浪在堤前平底、堤身及堤后平底處整個沿程的輻射應力和波浪增減水變化,并探究了堤前平底處輻射應力值受波幅偏移值的影響。

結果表明,數值模擬波浪在平底水槽中傳播的波形及輻射應力結果與解析結果吻合較好;在含潛堤地形的水槽中,得到了與實驗結果相吻合的破波區波面對比圖,并計算輸出了整個水槽內包括碎浪帶及堤后平底水槽處的波浪輻射應力變化,發現波浪完全破碎后堤后坡面及平底處輻射應力呈先增大后趨于平穩的趨勢,且堤后平底處較堤前平底處輻射應力值更大。

輻射應力結果與波浪增減水變化趨勢在碎浪帶內也能較好地對應波浪增減水方程;并且由于波浪反射造成的波幅的上浮與下沉,會間接導致輻射應力結果的增大與減小,且輻射應力值受波幅偏移值影響較為敏感。