楔塊重心位置對斜撐離合器性能的影響

嚴宏志 王志標 朱 楚 蔡孟凱 黎 佳 胡 璇

1. 中南大學輕合金研究院，長沙，410012 2. 中南大學機電工程學院，長沙，410012 3. 中南大學高性能復雜制造國家重點實驗室，長沙，410012 4. 中國航發湖南動力機械研究所，株洲，412002

0 引言

強制連續約束(positive continuous engagement，PCE)型斜撐離合器是直升飛機傳動系統中的一個重要部件，而楔塊是斜撐離合器的一個重要零件，通過楔塊與內外環的接觸和脫離可以實現離合器的接合和超越狀態。

目前，國內外學者對離合器工作過程中的動靜力學進行了一系列的研究。CHASSAPIS等[1]基于接觸力學理論，建立了離合器在傳動過程中的非線性動力學分析模型。XU等[2-4]建立了離合器的非線性數值分析模型，提出了離合器楔塊與內外環接觸為點-點接觸，得到了接觸力與溜滑角的數學模型，并通過實驗證明了相應結論。CHESNEY等[5]對偏心圓弧型面離合器楔角變化進行了分析，得到了楔角隨內外環半徑差增大而變大的結論，并得到了楔塊與內外環接觸應力數學模型。VERNAY 等[6]通過實驗分析了斜撐離合器在瞬時過載時的力學性能及楔塊與滾道接觸面微動磨損現象。CENTEA等[7]考慮離合器慣性、尺寸和楔塊與內外環接觸力等參數，建立了斜撐離合器的非線性多體動力學模型。ROACH等[8]從離合器接合方式、承載能力方面對彈簧離合器、滾柱離合器和斜撐離合器進行了對比研究與評價。CHEN等[9]研究了多種規格楔塊的斜撐離合器的接觸特性。朱自冰[10]對斜撐離合器楔角、接觸應力、變形、升程等參數進行了研究分析。楊振蓉[11]對斜撐離合器設計方法進行了研究，通過疲勞實驗、過載實驗等對離合器進行了研究，并分析了實驗結果。嚴宏志課題組[12-18]對PCE型斜撐離合器進行了系統研究：基于Hertz理論與厚壁圓筒理論，得到了Hertz應力數學模型，求解了斜撐離合器楔塊Hertz接觸應力、周向壓應力、內外環楔角與變形等參數隨負載的變化曲線[12-13]；對偏心圓弧、阿基米德曲線和對數曲線3種型面楔塊進行了參數化設計，建立了動靜力學分析模型并對楔塊型面進行了優化[14]；對斜撐離合器磨損進行了研究，并基于磨損量對斜撐離合器失效進行研究[15]；研究了不同楔角對數型面斜撐離合器接觸特性，并對楔塊型面進行了優化[16]；對阿基米德斜撐離合器楔塊型面進行了修形設計，并分析了其性能[17]；研究了輸入轉速波動下斜撐離合器的動態接合特性[18]。然而，重心位置對離合器性能影響規律的研究未見相關報道。

本文研究PCE型斜撐離合器楔塊重心位置對離合器性能的影響，為不同工作模式的離合器楔塊重心位置的設計提供理論依據。

1 楔塊重心位置的求解方法

PCE型離合器結構如圖1所示。

1.楔塊 2.保持架 3.內環 4.外環 5.注油孔 6.彈簧 7.軸承圖1 PCE型離合器結構示意圖Fig.1 Schematic diagram of PCE clutch

1.1 楔塊受力分析

楔塊在運動過程中，其重心與它繞自身旋轉的中心不重合。當楔塊重心位于旋轉中心左側時，楔塊產生的離心力會導致楔塊與內外環的接觸力增大，有利于楔塊與內外環楔緊。當楔塊重心位于旋轉中心右側時，楔塊產生的離心力會導致楔塊與內外環的接觸力減小，可以減小楔塊與內外環之間的磨損。超越狀態和正常傳動狀態下不同重心位置的楔塊受力如圖2和圖3所示，圖中Fr為彈簧對楔塊徑向力，Fn(o)為外環對楔塊法向力，Fn(i)為內環對楔塊法向力，Cg為楔塊重心位置，Cr為楔塊旋轉中心位置，Fcen為離心力。

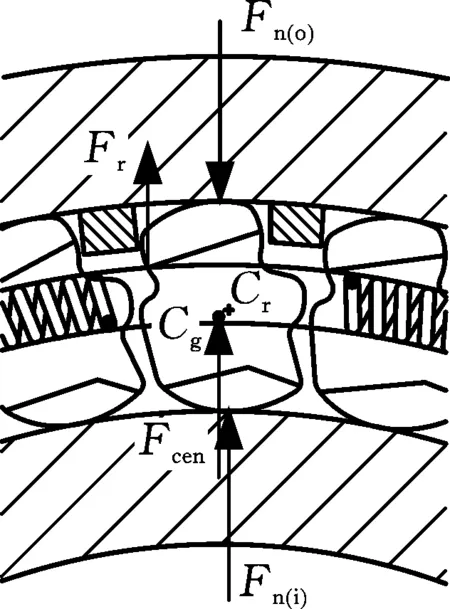
(a) 重心在左側

(b) 重心在右側

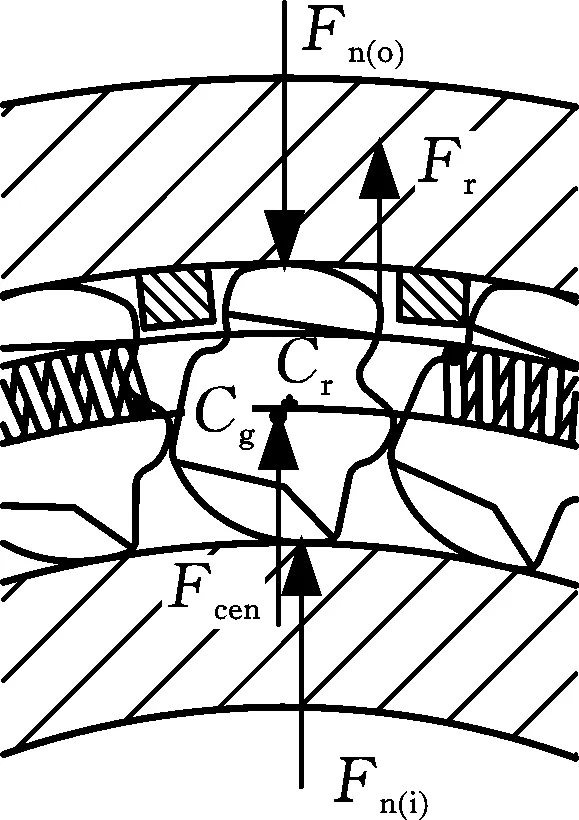
(a) 重心在左側

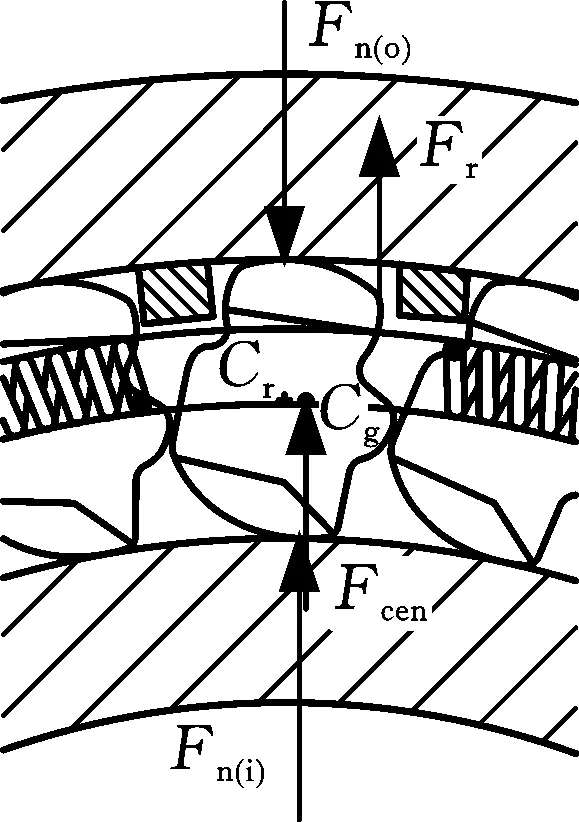
(b) 重心在右側

1.2 楔塊重心位置求解模型

1.2.1楔塊設計坐標系下重心位置模型

斜撐離合器中楔塊的幾何形面由圓弧與直線組成，是一個不規則的幾何圖形。要求解其重心位置，可以將其分成若干三角形及弓形，分別求出這些圖形的重心，再通過疊加法求出楔塊重心位置，分解后的楔塊截面如圖4所示。

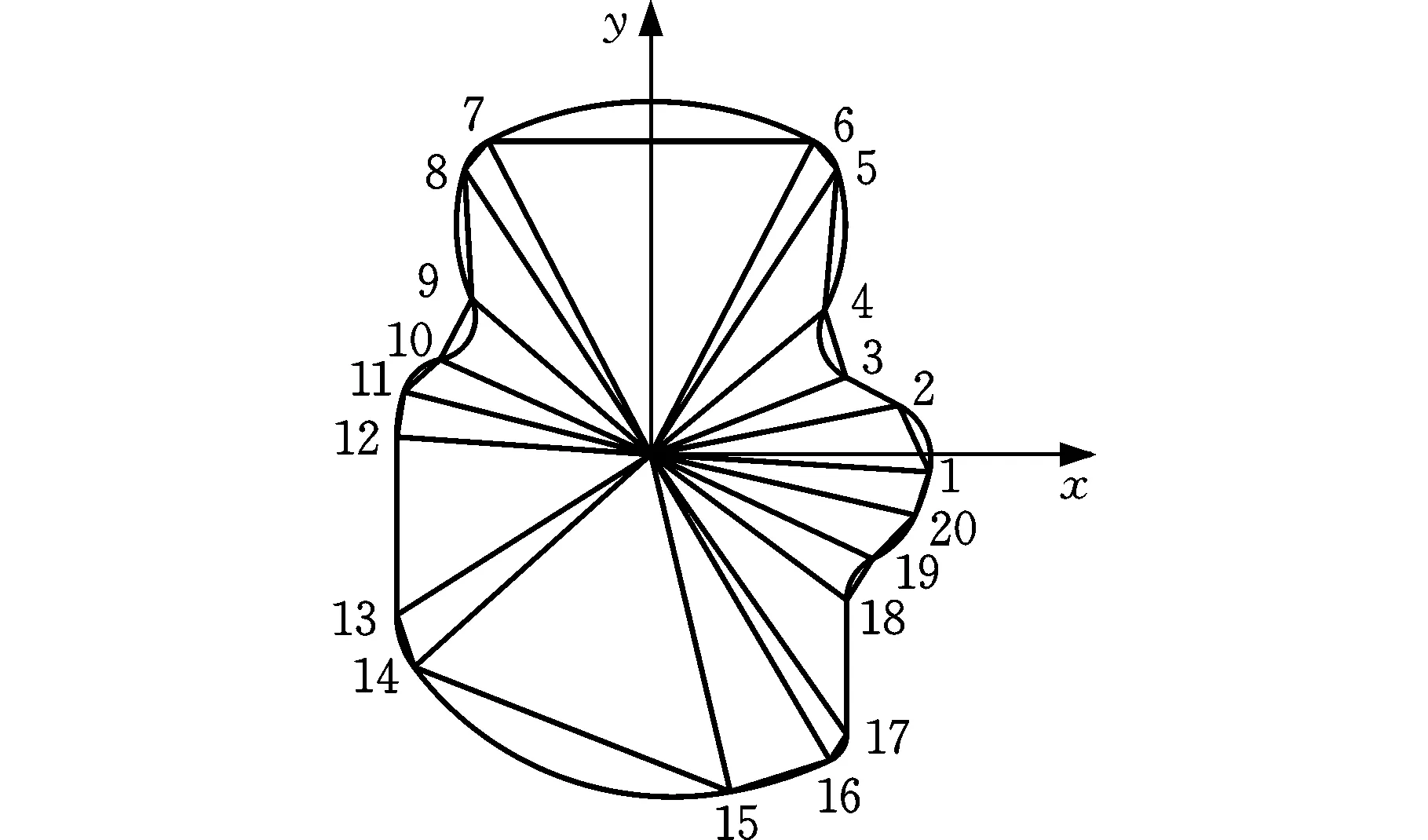
圖4 楔塊截面組成Fig.4 Sprag section composition

按照上述方法將楔塊形面分解后，計算三角形的重心坐標和面積，三角形的幾何坐標如圖5所示。分解后的三角形的3個頂點坐標分別為O(xO，yO)、A(xi，yi)、B(xi+1，yi+1)，則三角形的重心gOi(xOi，yOi)和面積SOi可表示為

(1)

(2)

(3)

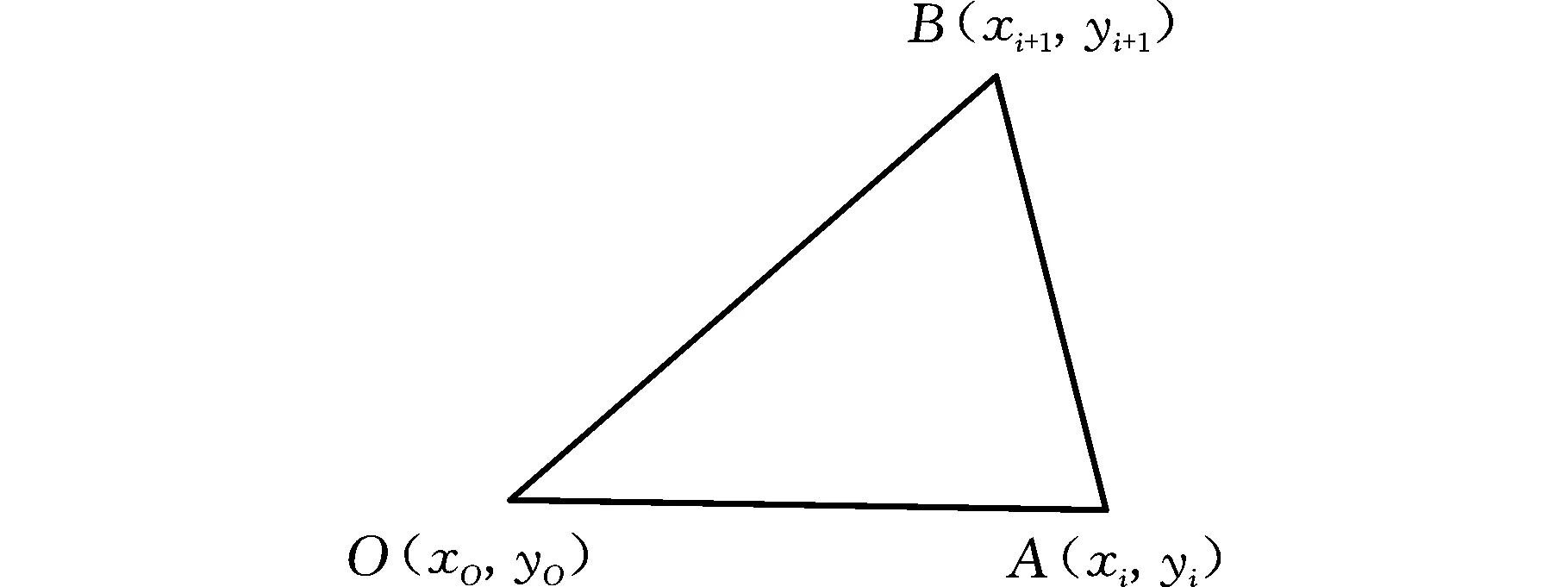
圖5 三角形幾何坐標圖Fig.5 Triangle geometry

計算分解后每個弓形的重心坐標和面積，弓形的幾何坐標圖見圖6。已知弓形的圓心坐標為Oi(xOi，yOi)，圓弧起點坐標為A(xi，yi)，圓弧終點坐標為B(xi+1，yi+1)，則弓形的重心g1i(x1i，y1i)可由扇形OiAB與三角形OiAB重心疊加求出，三角形OiAB重心坐標(xOg1，yOg1)及面積SO1可表示為

(4)

(5)

(6)

扇形OiAB重心坐標(xOg2，yOg2)及面積SO2可表示為

(7)

(8)

(9)

由式(4)～式(9)可以得到弓形OiAB重心坐標(xOi，yOi)及面積SOi表達式：

(10)

(11)

SOi=SO2-SO1

(12)

圖6 弓形幾何坐標圖Fig.6 Arch geometry

按照上述計算方法得到每一個三角形和弓形的重心位置與面積后，由疊加法可計算楔塊截面的重心坐標(xj，yj)，其表達式為

(13)

(14)

由于PCE型斜撐離合器形狀復雜，且兩端開有凹槽，故在計算重心位置時上述公式只能用于中間段計算，要求得實際重心位置，還需將其分為左中右3段，如圖7所示。在求出每段重心位置及體積后，通過下式疊加求出楔塊重心Cg(x，y)：

(15)

(16)

式中，Vj為楔塊每段體積。

圖7 楔塊三維幾何模型Fig.7 3D geometric model of the sprag

1.2.2不同工況下楔塊重心位置模型

我國1998年頒布的《建設項目環境保護管理條例》第15條規定公眾參與主體為“建設項目所在地的有關單位和居民”。2002年《環境影響評價法》則用“公眾”代替了“居民”，體現了公眾參與主體范圍的擴展。但目前我國在不同的法律、法規、規章和行政規范性文件中，大都只是提到“公眾”一詞，缺乏對“公眾” 進一步的概念界定。相關立法中有關“公眾”的含義，有狹義上的“公眾”，即公民，將其與單位和專家并提，獨立于單位和專家之外；廣義上的“公眾”，包括單位和個人，單位和居民，有關部門、組織、專家，建設項目周圍單位、個人；最廣義上的“公眾”包括任何單位和個人。具體而言，有以下幾種情形：

在不同扭矩作用下斜撐離合器楔塊楔緊時所處的位置不同，楔塊旋轉后的位置需要根據迭代公式求解，同理，楔塊旋轉后的重心位置可以根據坐標變換原理求解。

(1)空間齊次坐標變換原理。根據齊次坐標變換原理，當基坐標系S沿X軸、Y軸、Z軸平移距離x、y、z得到變換后的坐標系T時，兩坐標系的齊次變換矩陣如表1所示。當基坐標系S沿X軸、Y軸、Z軸轉動角度α、β、γ得到變換后的坐標系R時，兩坐標系的齊次變換矩陣如表1所示。

表1 齊次坐標變換矩陣

(2)楔塊在不同工況下重心位置模型。依據上述齊次坐標變換原理，楔塊從設計坐標系O2X2Y2到離合器基坐標系O1X1Y1的齊次變換矩陣

(17)

其中，楔塊設計坐標系O2X2Y2原點為楔塊上凸輪圓弧圓心，離合器基坐標系O1X1Y1原點為離合器內外環圓心，楔塊在不同坐標系下的示意圖見圖8。

圖8 楔塊在不同坐標系下的示意圖Fig.8 Schematic diagram of sprag in different coordinate systems

依據坐標變換，可計算出楔塊重心位置Cg在離合器基坐標系O1X1Y1下的坐標值，變換矩陣為

(18)

(19)

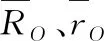
(20)

2 楔塊重心位置對離合器性能影響分析

2.1 斜撐離合器動力學建模

(1)材料選擇。在斜撐離合器工作過程中，楔塊需承受交變載荷，要求其強度高、耐磨性好，可以采用軸承鋼GCr15，內外環和保持架采用18CrNi4A鋼，離合器各部件材料參數如表2所示。

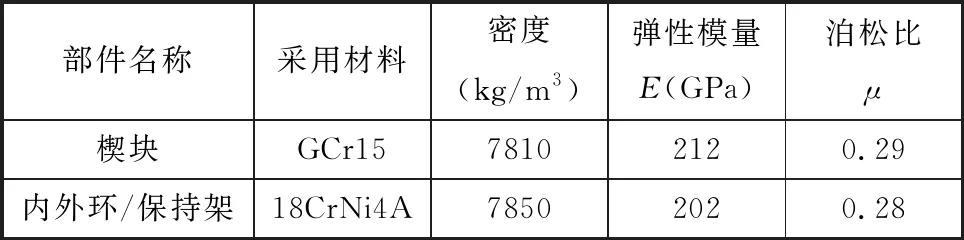
表2 斜撐離合器各部件材料參數

(2)邊界與初始條件的施加。對斜撐離合器的結構和接觸情況等作如下假設和簡化：①忽略斜撐離合器在制造和安裝過程中產生的誤差；②各部件視為剛體；③楔塊均勻地承受彈簧彈力。根據斜撐離合器的工作原理，添加相應的負載和運動激勵來實現離合器的運動，構建的離合器虛擬樣機模型如圖9所示。施加邊界條件及載荷如下 ：①內外環的運動副均為旋轉運動，分別在其中心設置對Ground的Joint約束；②對楔塊與內外環和保持架施加接觸約束；③在接合過程中，外環為驅動元件，因而對外環施加轉速運動，內環為被驅動元件，因而對內環添加一個恒負載轉矩，分別對33個楔塊施加彈簧的作用力矩，加載曲線如圖10所示；④設定重力加速度為9.8 m/s2。

圖9 斜撐離合器虛擬樣機模型Fig.9 Diagonal clutch virtual prototype model

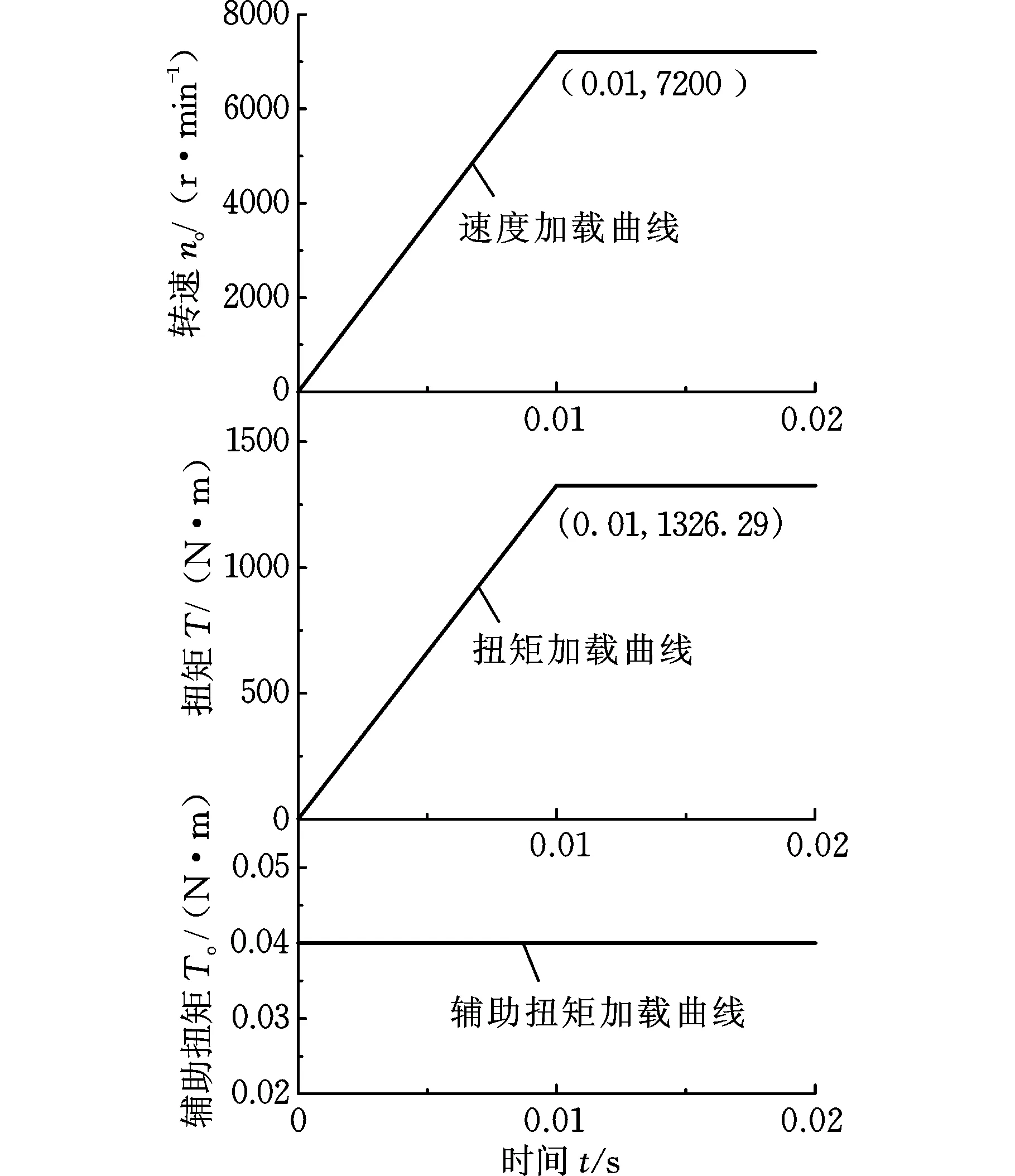
圖10 加載曲線Fig.10 Loading curve

2.2 楔塊重心位置對接觸壓力的影響

按照圖10加載條件，對3組不同重心位置楔塊進行動力學仿真，得到楔塊與內外環接觸力與重心位置關系，如圖11和表3所示。由圖11及表3可得，在離合器接合過程中，楔塊重心在旋轉中心左側且離中心距離為0.01 mm、0.03 mm、0.05 mm時，楔塊與內外環接觸力增大，說明重心位于左側時能適量增加楔塊與內外環接觸力，有利于楔合。

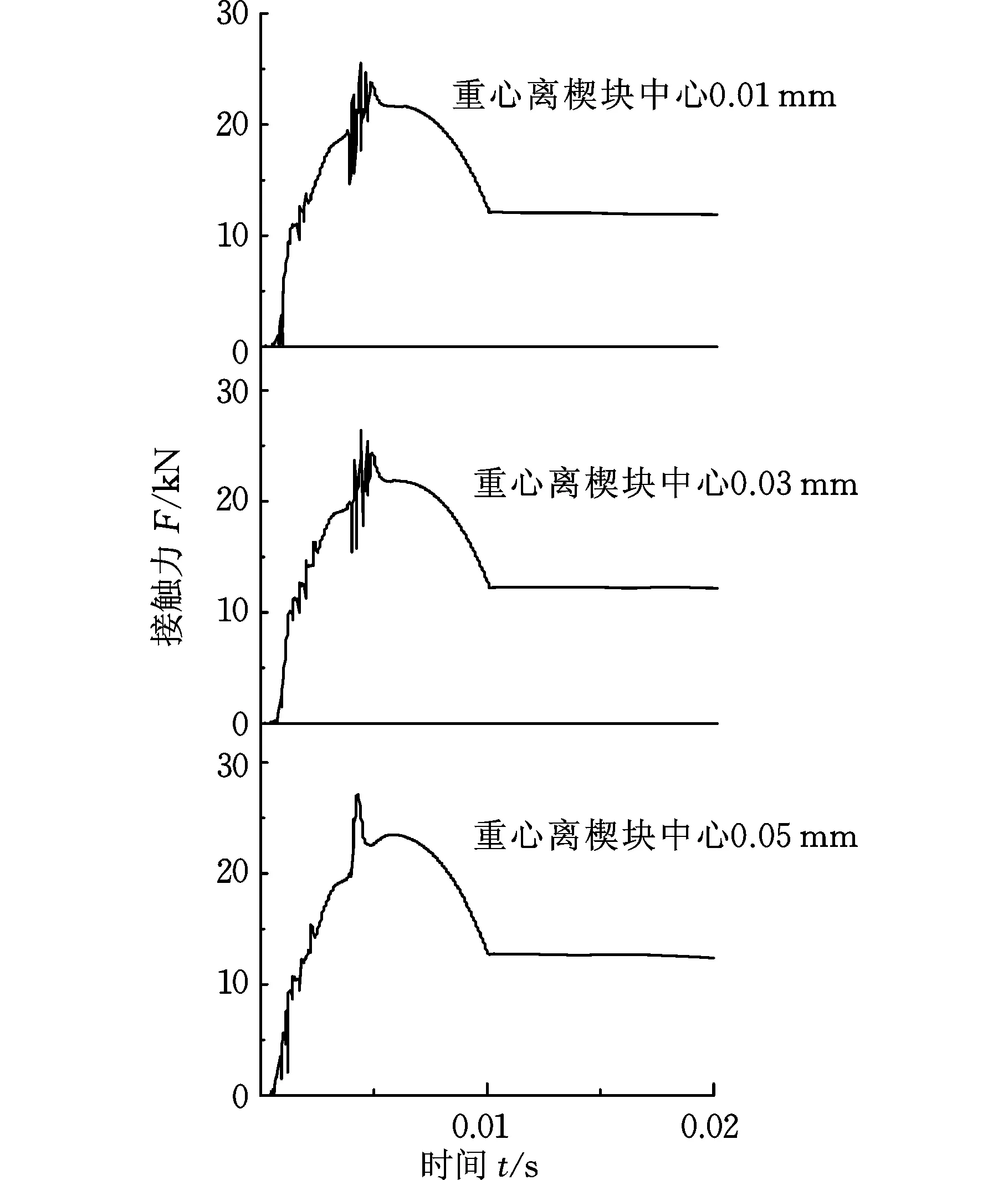
圖11 接觸力隨時間變化曲線(左側)Fig.11 Contact force varies with time(left)

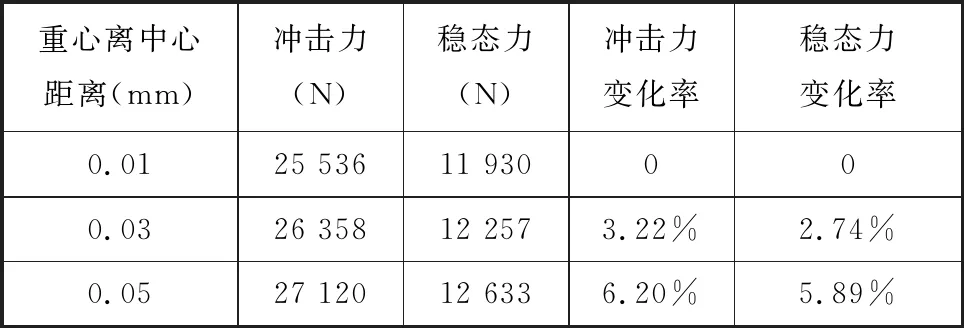
表3 楔塊與內外環接觸力大小及變化率(左側)

對重心位置位于旋轉中心右側且離中心距離分別為0.01 mm、0.03 mm、0.05 mm的3組楔塊進行動力學仿真，得到楔塊與內外環接觸力與重心位置關系如圖12和表4所示。由圖12及表4可得，在離合器接合過程中，楔塊重心在旋轉中心右側且離中心距離為0.01 mm、0.03 mm、0.05 mm時，楔塊與內外環沖擊力和穩態力都減小，說明重心位于右側時會減小楔塊與內外環接觸力，減小磨損，但不利于楔合。

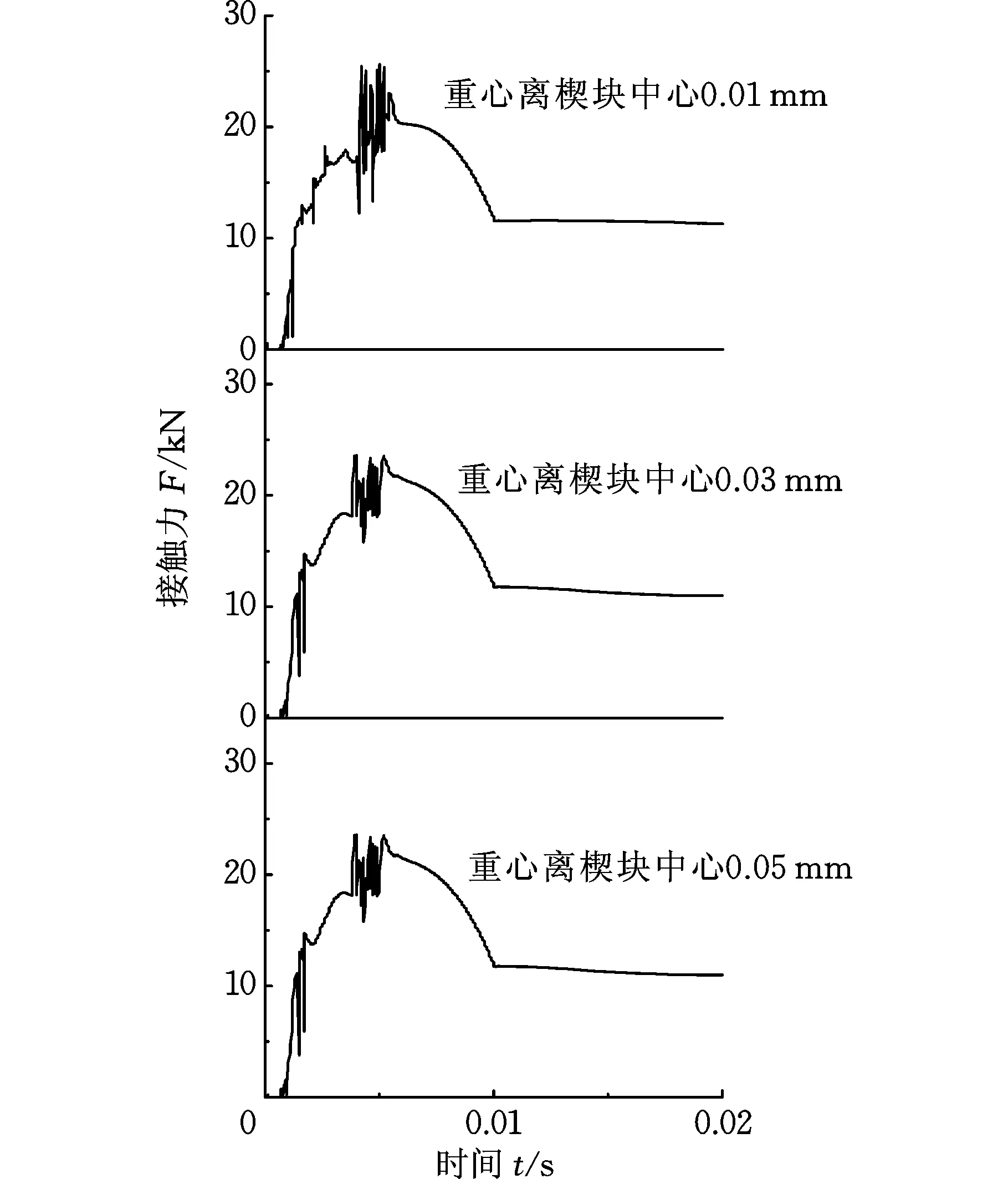
圖12 接觸力隨時間變化(右側)Fig.12 Contact force varies with time(right)

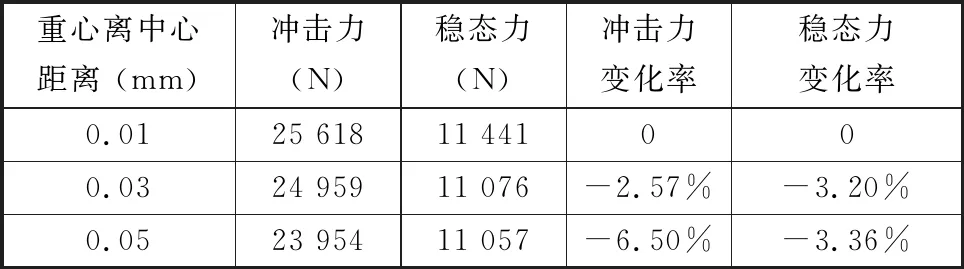
表4 楔塊與內外環接觸力數值及變化率(右側)

2.3 楔塊重心位置對接合脫開性能影響分析

按照圖10加載條件，對重心位置位于旋轉中心左側且與中心距離分別為0.01 mm、0.03 mm、0.05 mm的3組楔塊進行仿真，得到離合器接合規律，如圖13及表5所示，圖中點A為離合器接合時間點。

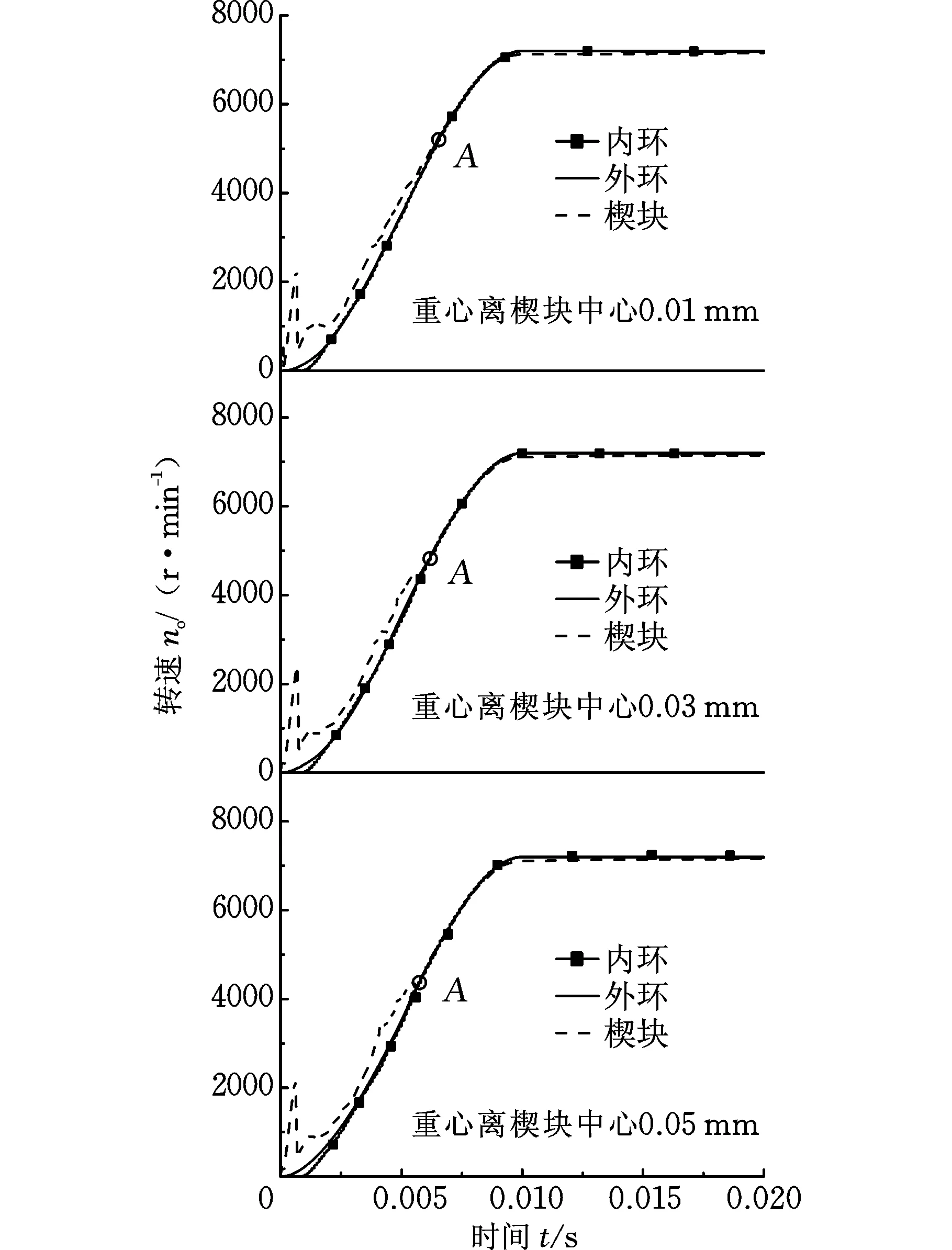
圖13 楔塊與內外環轉速隨時間變化曲線(左側)Fig.13 Speed curves of sprag and inner-outer ring vary with time(left)

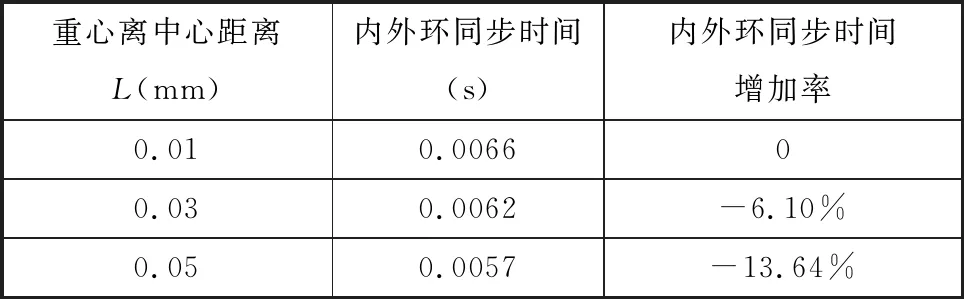
表5 重心對接合性能的影響(左側)

由圖13及表5可得，楔塊重心在旋轉中心左側時，離合器內外環同步時間縮短，重心距離旋轉中心0.05 mm比距離0.01 mm時內外環同步時間縮短13.64%，因此，楔塊重心位于左側有利于接合。

按照圖10加載條件，在0.02 s之后將外環減速到0，仿真重心位置位于旋轉中心右側0.01 mm、0.03 mm、0.05 mm的3組楔塊，得到離合器接合規律，如圖14及表6所示，圖14中點B為離合器響應時間點，點C為離合器脫開時間點，脫開時間為BC段。

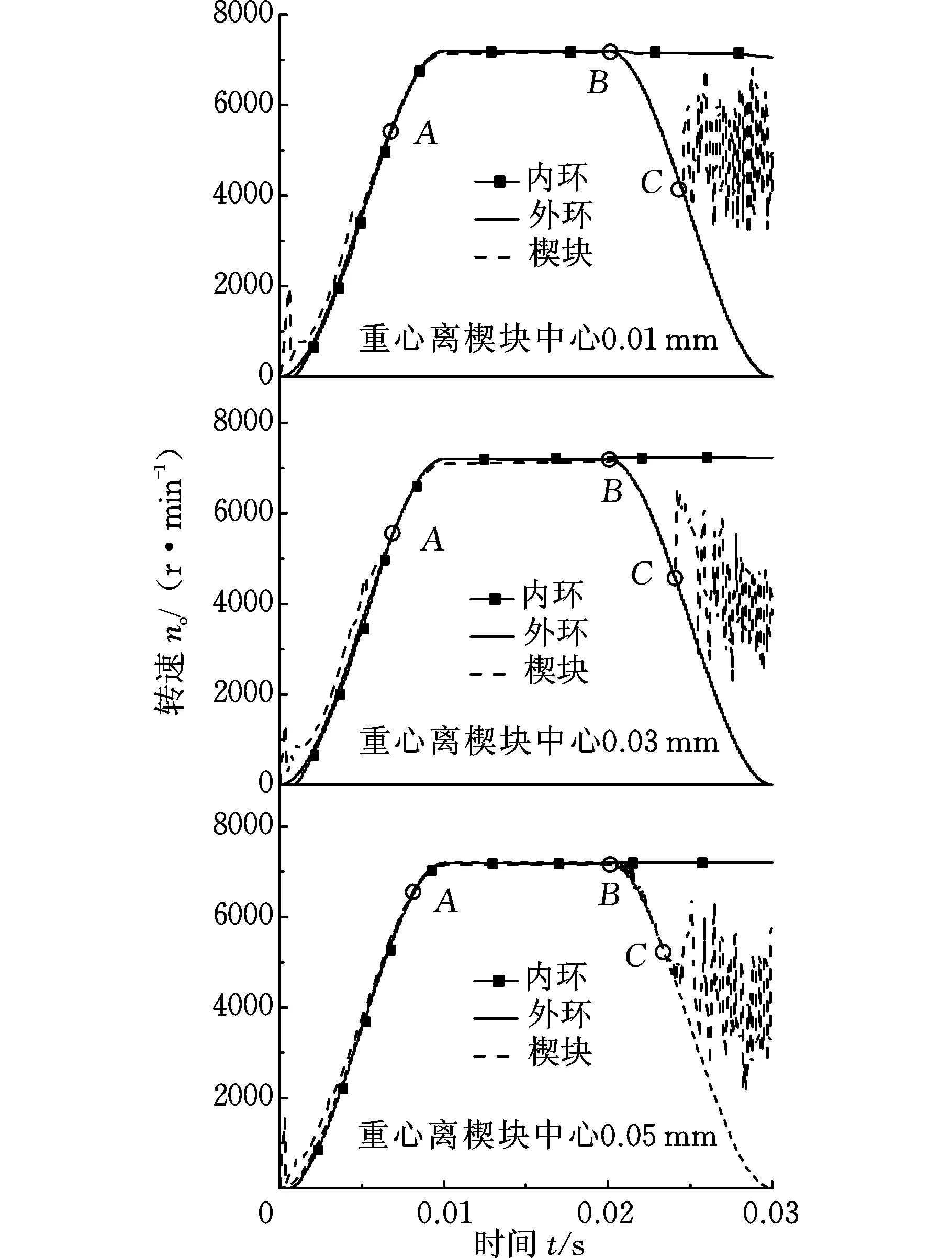
圖14 楔塊與內外環轉速隨時間變化曲線(右側)Fig.14 Speed curves of sprag and inner-outer ring vary with time(right)

表6 重心對接合性能的影響(右側)

由圖14及表6可得，在離合器接合過程中，楔塊重心在旋轉中心右側時，離合器脫開時間短，重心距離旋轉中心0.05 mm比距離0.01 mm時內外環同步時間增長19.12%，脫開時間縮短20%，因此，楔塊重心位于右側有利于脫開。

3 實驗驗證

為了驗證上述分析的結論，設計重心在旋轉中心左側且與中心距離分別為0.01 mm、0.03 mm、0.05 mm的3組楔塊，實物見圖15，并搭建圖16所示的斜撐離合器實驗臺，完成斜撐離合器的動力學測試實驗。

圖15 三組楔塊實物圖Fig.15 Three sets of sprags

1.驅動電機 2、4、12、15.聯軸器 3.扭矩傳感器 5、11、14.磁環非接觸式編碼器 6、10.軸承支架 7、9.脹緊套 8.斜撐離合器 13.齒輪減速器 16.負載電機 圖16 斜撐離合器實驗臺Fig.16 Sprag clutch test bench

驅動電機的設置轉速為2 000 r/min，負載電機設置負載扭矩10 N·m，測試3組楔塊接合性能，通過光柵尺測量輸入輸出轉速，得到輸入輸出轉速時域圖，每組楔塊測試3次，得到實驗數據取平均值，結果如圖17所示。

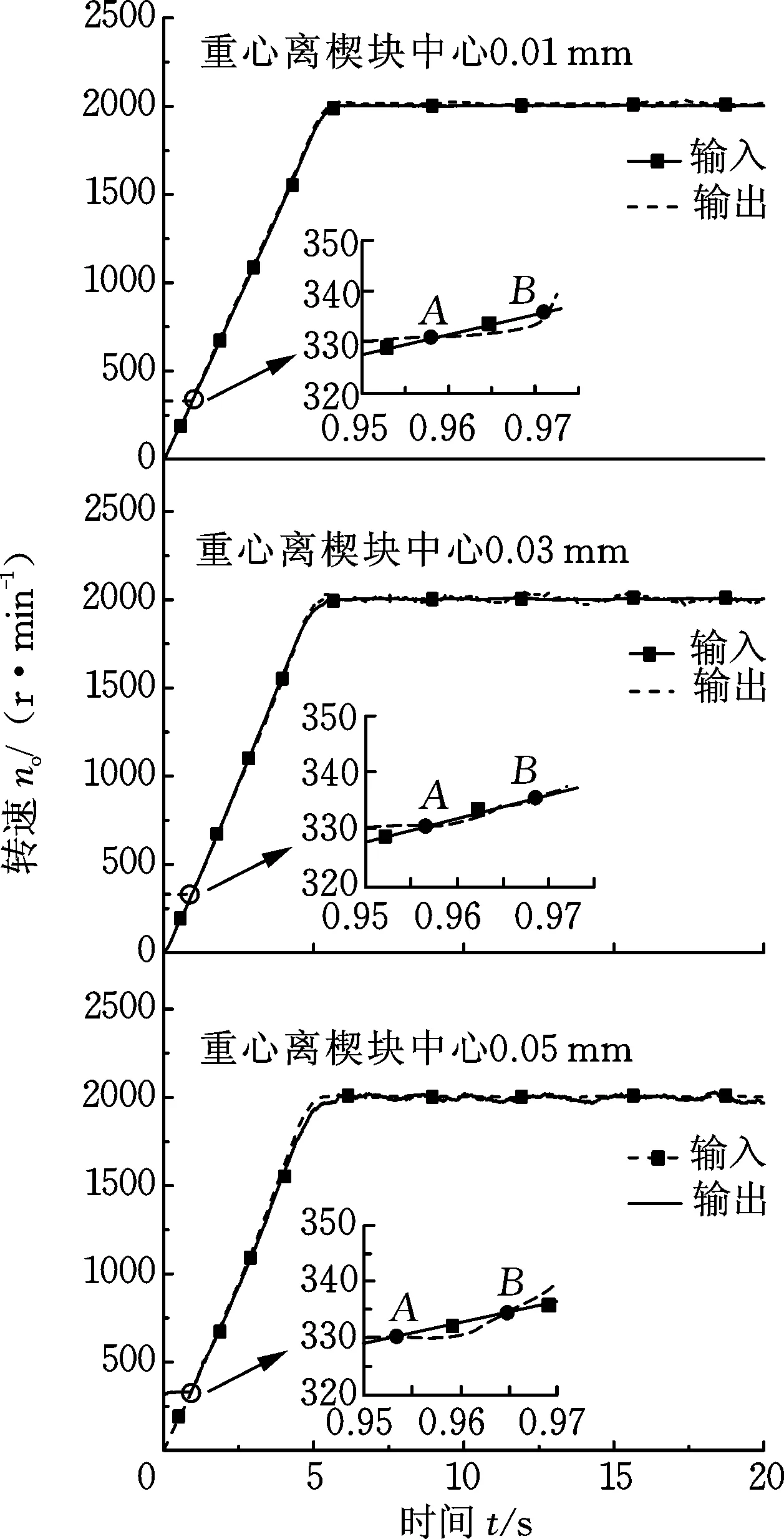
圖17 楔塊實驗結果Fig.17 Test results of sprag

實驗中，先啟動負載電機，離合器處于超越狀態，內環轉動，再反向啟動驅動電機使得離合器接合，A點為響應時間點，B點為接合時間點，A、B點時間差值為內外環同步時間，不同重心位置楔塊內外環同步時間實驗結果如表7所示。

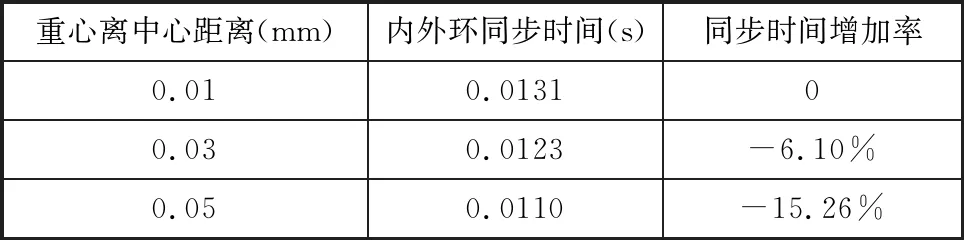
表7 不同重心位置內外環同步時間

由于離合器存在制造安裝誤差，實驗加載的轉速及負載小于實際工況，所以實驗比仿真得到接合時間長，但是3組楔塊對比得到的接合時間增加率與仿真結果吻合，表明楔塊重心在旋轉中心左側時能夠提高楔塊接合性能。

4 小結

(1)楔塊重心位置在旋轉中心左側時，接合過程產生的離心力能夠適量地增大其與內外環接觸力，在右側時減小接觸力，楔塊重心到旋轉中心距離為0.05 mm比距離為0.01 mm時接觸力增大(左側)或減小(右側)了6%左右。

(2)楔塊重心離旋轉中心左側越遠，越有利于離合器接合。當楔塊重心位于旋轉中心右側時，脫開時間縮短，表明有利于楔塊脫開。

(3)在實際使用中，斜撐離合器主要用于接合狀態時，可根據重心位置模型設計楔塊重心在旋轉中心左側；主要用于超越狀態時，設計楔塊重心在旋轉中心右側。