基于改進型非線性干擾觀測器的爬壁機器人軌跡跟蹤①

曹錦波,潘海鵬,張益波

(浙江理工大學 機械與自動控制學院,杭州 310018)

爬壁機器人由于其可以在高空作業的特殊性廣泛應用于船舶噴漆除銹、油罐檢測等行業[1,2].其中履帶式磁吸附爬壁機器人作為一種較為常見的爬壁機器人,是典型的非線性多輸入多輸出系統.在壁面爬行過程中履帶機器人容易受到重力及外部干擾等因素影響,從而導致機器人實際位姿與理想位姿的誤差.為了解決這一問題,文獻[3,4]只從機器人運動學出發設計控制PID、反演控制等算法,但這沒有考慮機器人的動力特性,在實際運用中其控制算法具有一定的局限性且對外部干擾的抑制效果較差.因此,很多學者結合運動學和動力學進行研究,并利用模糊控制、神經網絡控制、魯棒自適應控制等算法進行軌跡跟蹤控制[5–8],智能算法能呈現出較好的跟蹤效果并抑制外界干擾,但算法比較復雜,實用性與實時性不高.

本文參考輪式機器人的研究及爬壁機器人運動的特點,受文獻[9]啟發在研究爬壁機器人運動學與動力學的基礎上對控制算法上進行改進.本文將建模誤差與外部干擾作為系統的總體擾動,通過改進型非線性干擾觀測器[10]對該擾動進行觀測作為前饋控制,使擾動誤差以指數形式收斂,并采用反演控制作為運動學控制,采用滑模反演控制作為動力學控制,使動力學控制算法收斂速度快于運動學算法收斂速度,避免造成閉環系統的不穩定.最后使用Lyapunov 方法驗證了系統的穩定性.仿真結果驗證了該算法的有效性.

1 履帶式爬壁機器人模型

根據爬壁機器人的機械結構及工作環境特點,做出以下假設:

(1)在平直二維壁面內工作;

(2)爬壁機器人為剛體,且質量分布均勻,其重心與幾何中心重合;

(3)理想滾動條件,爬壁機器人無滑移,運動瞬時方向即機器人本體坐標系X'軸方向.

根據以上假設,本文研究的履帶式機器人運動模型可簡化為圖1所示.

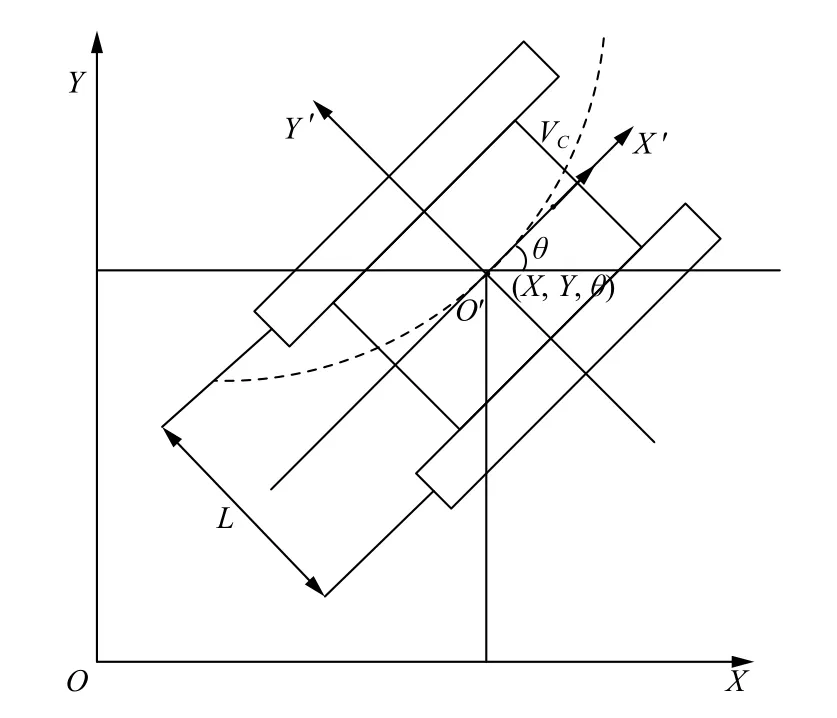
圖1 爬壁機器人運動模型

1.1 運動學模型

履帶式爬壁機器人實現轉向運動主要有給予兩輪相反速度和給予兩輪方向相同但大小不同速度兩種方法,本文采用第二種方法.(X,Y)為爬壁機器人在全局坐標系XOY下的質心坐標;(X′,Y′)為機器人本體坐標系X'O'Y'中的坐標;θ為機器人運動方向與X軸的夾角,其中 θ 的范圍為[0,2π);(ωL,ωR)為爬壁機器人的左右輪角速度,即爬壁機器人的輸入控制量;R為機器人車輪半徑;L為車身寬度.那么機器人位姿可用來表示機器人的運動學方程表示為:

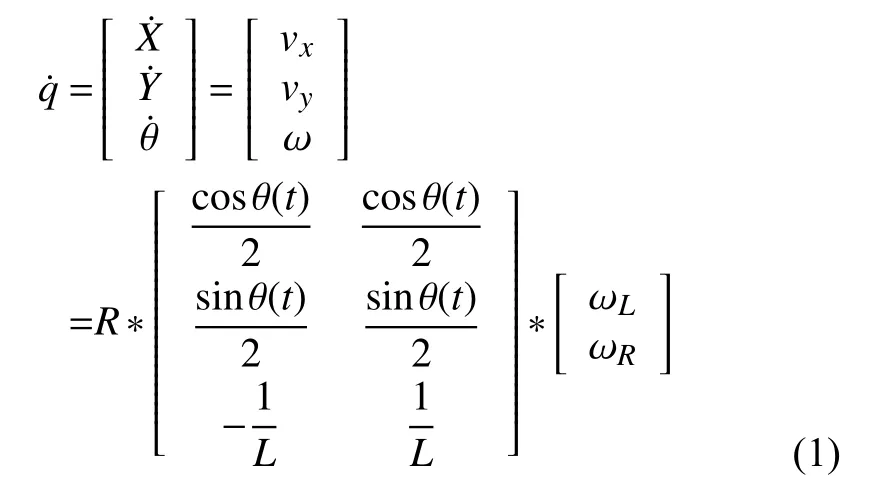
其中,vx為機器人速度在X軸方向的分量,vy為機器人速度在Y軸方向的分量.

又有:

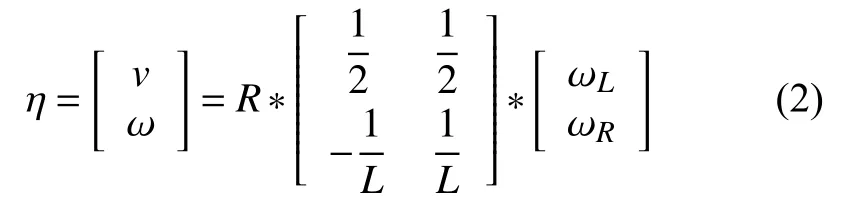
其中,v為質心速度,ω為質心角速度.為方便控制,將式(2)代入式(1),狀態方程簡化為:

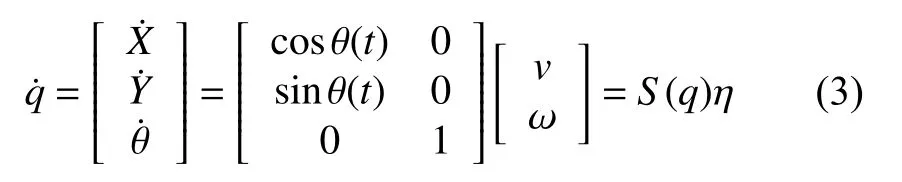
此時控制量變為v、ω,機器人滿足非完整約束條件:

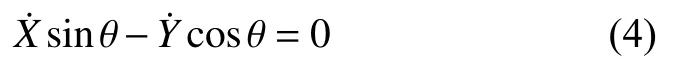
1.2 動力學模型

針對履帶爬壁機器人的瞬態動力學進行研究,根據文獻[11,12],假設兩側履帶受到的摩擦力相同,將機器人模型簡化如圖2所示.那么根據牛頓力學對機器人系統進行動力學分析,當無外界干擾時,對于機器人本體坐標系有:

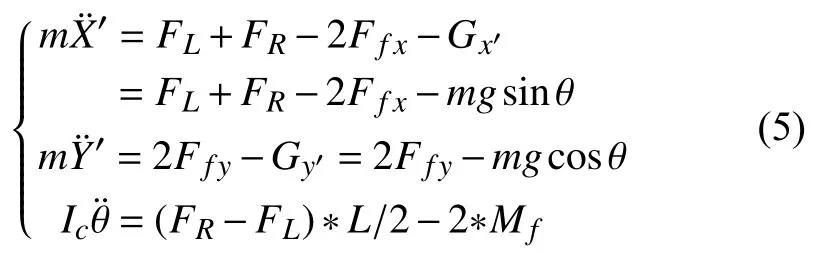
其中,FR=τR/r,FL=τL/r,τR、τL分別為左右電機驅動力矩,r為履帶車輪半徑;m為履帶式爬壁機器人本體質量;Ic為機器人本體對質心的轉動慣量;Ff x為單側履帶縱向摩擦力;Ffy為單側履帶橫向摩擦力;Mf為單側履帶摩擦阻力矩.

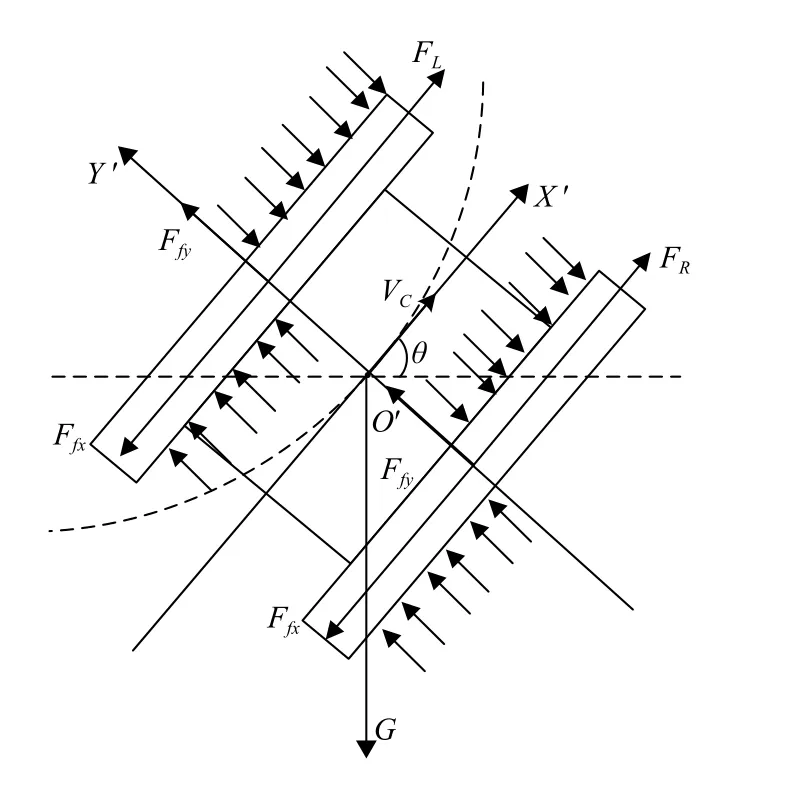
圖2 履帶機器動力學模型

將動力學方程從本體坐標系轉化為全局坐標系可得:

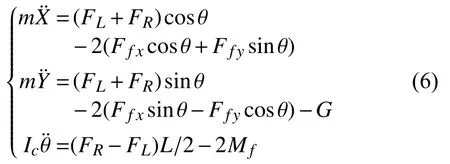
由以上公式可知,當加入未知有界外部干擾時,簡化的爬壁機器人動力學方程用標準拉格朗日動力學模型可表示為:

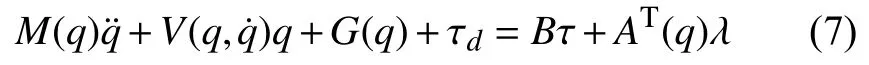
觀察式(7),機器人的重力和摩擦力矩陣在實際應用中較難測得,故將其與外界擾動視為系統總擾動.又ST?AT=0故 在式(7)兩邊同時左乘ST(q)以去掉約束力.同時對式(3)求導可得=+,將其也代入式(7),則爬壁機器人動力學方程等效為:

2 軌跡跟蹤控制器設計

由上一部分內容可知,本文中將動力學的重力、摩擦力作用及外部干擾視為系統總擾動,系統建模存在誤差,故采用改進型非線性干擾觀測器對該部分進行前饋補償.

系統控制器(圖3)設計首先對運動學模型采用反演控制算法得出爬壁機器人參考速度和角速度.其次針對動力學模型設計基于改進型非線性干擾觀測器的滑模控制算法,使系統具有較強的魯棒性.

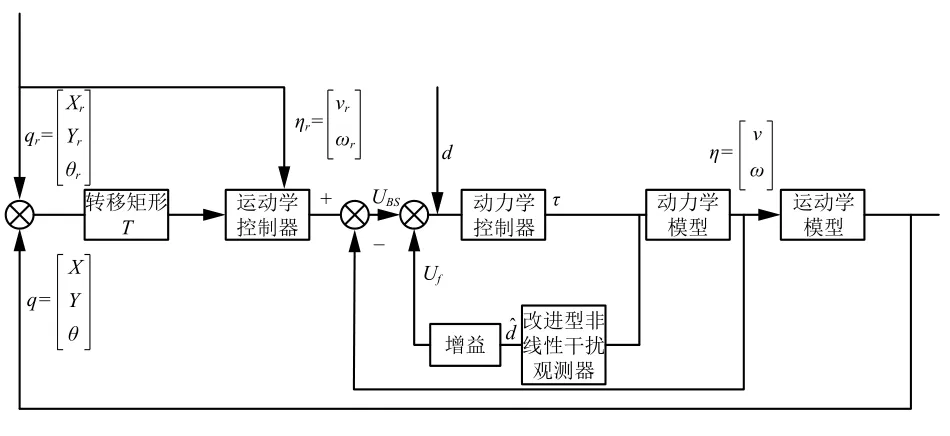
圖3 控制器框圖

2.1 運動學控制器

爬壁機器人在全局坐標系的位姿誤差如圖4所示,則機器人在本體坐標系上的位姿誤差可定義為:

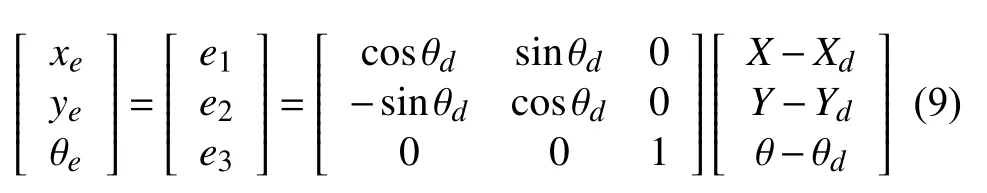
參考文獻[13],得到機器人運動學控制律為:

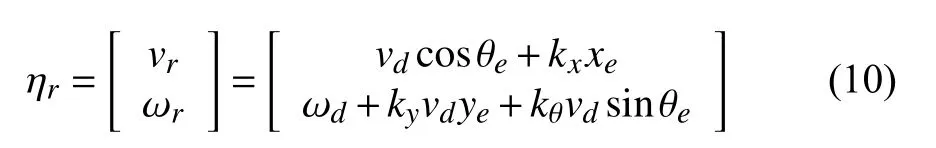
其中,vd、ωd為爬壁機器人設定軌跡的理想速度與角速度,kx、ky、kθ均為正數.此時定義Lyapunov 函數為:

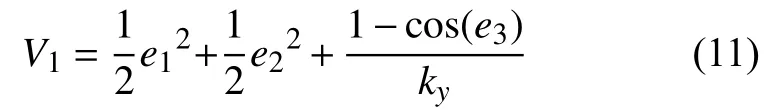
其中,e3∈[?π,π],顯然對于任意界限內0,有V1＞0,V1正 定.對V1求導得:

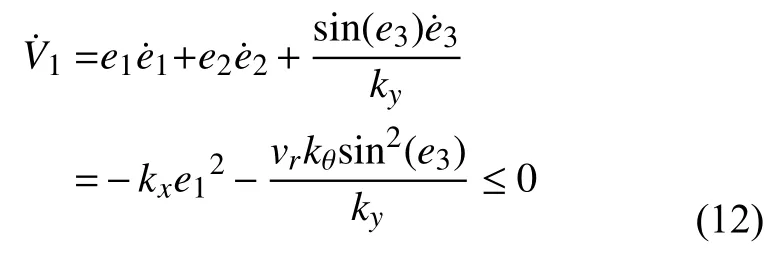
由于 sin(e3)的存在,存在e3≠0 時=0,故半負定,且不恒等于0,時V1→∞.故根據Lyapunov 定理可得平衡狀態是局部漸近穩定的.

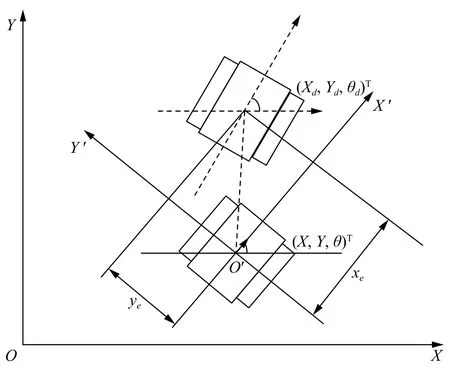
圖4 爬壁機器人軌跡跟蹤

2.2 改進型非線性干擾觀測器

對于外界干擾,普通非線性干擾觀測器一般將擾動d的導數近似成=0,而實際環境中一般不為0,故觀測效果始終存在誤差.根據機器人系統動力學模型,參考文獻[14,15],對于系統=f(x)+g(x)u+d,設計改進型非線性干擾觀測器如下所示:

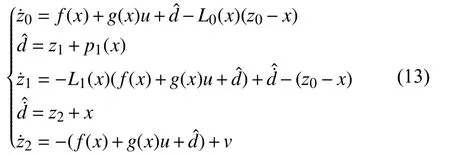
其中,為實際干擾d的估計值;為實際干擾導數的估計值;Li(i=0,1)為觀測器增益,v為引入的虛擬控制函數.

設計控制律[16]:相較于文獻[14,15],該觀測器對、、的設計進行了改進,對于在等式右邊增加“?(z0?x)”,修改=z2+L2x為=z2+x從而設計的控制律更為簡單.該觀測器相較于文獻[14,15]需設計的參數更少,并且采用了飽和函數替代符號函數,削弱抖振.

在實際環境中影響爬壁機器人位姿的原因主要為磁吸附力不足,并受重力影響從而造成爬壁機器人發生滑移.故干擾主要為磁吸附力及重力,其變化一般緩慢,其n階導滿足條件:

即干擾及其任一階導有界.

定義改進型非線性干擾觀測器的觀測誤差為:

則,

變換等式得:

令Lyapunov 函數為:

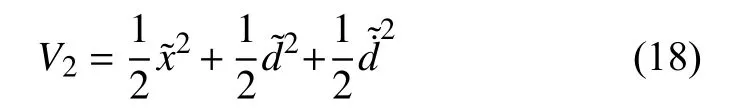
顯然V2≥0,有且僅當、、等于零時,V2=0,V2正定.對V2求導得:

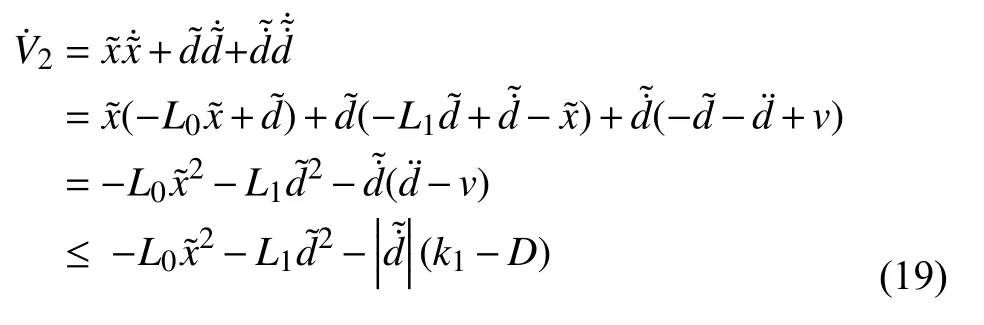
為滿足Lyapunov 定理,取L0＞0,L1＞0,k1≥D,使得≤0.

2.3 動力學控制器

通過設置增益將干擾觀測器觀測到的干擾轉化為相應干擾輸入控制量,即:

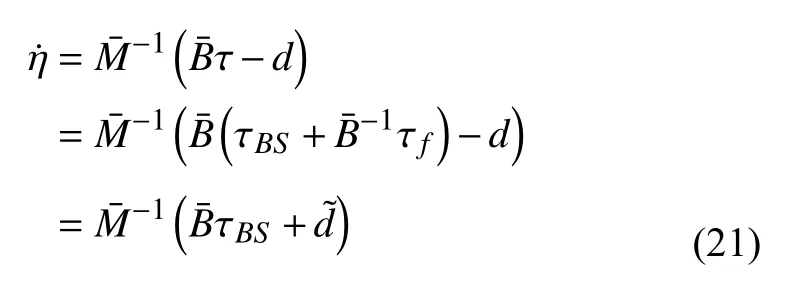
由上式可知,采用相應干擾觀測器后,系統的干擾減少,根據轉變后的系統設計動力學控制器.

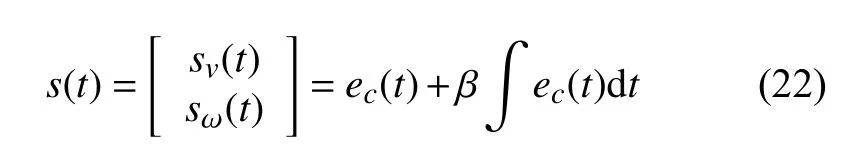
其中,β＞0.對滑動面求導得:

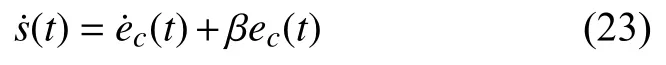
將式(21)代入式(23)得:

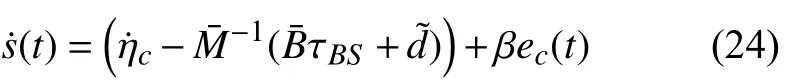
設計的滑模控制主要包括2 個部分:等效控制和切換控制,即:

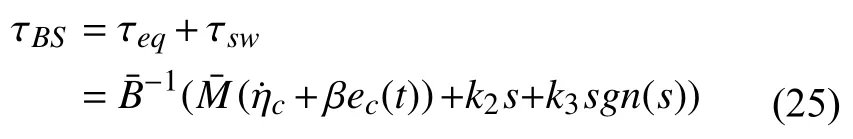
但為了削弱“抖振”現象,引入變速函數[17]vs(S,ε)=代替符號函數sgn(s).

令Lyapunov 函數為:

則有式(27):

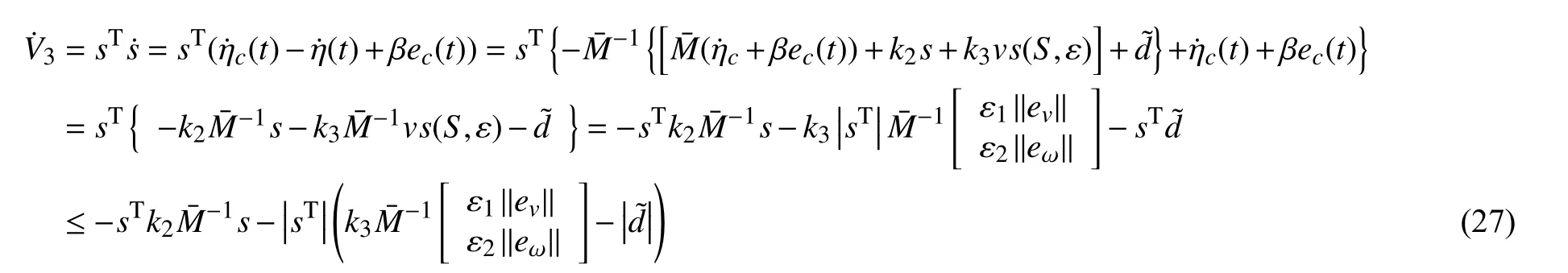
要使系統穩定則k2≥0且此時≤0.

綜上所述,對于整個閉環系統,考慮Lyapunov 函數:根據Lyapunov定律可知整個閉環系統是漸近穩定的.

3 Matlab 仿真驗證

以履帶式機器人為研究對象,機器人參數為:m=10 kg,I=5 kg·m2,r=0.05 m,L=1 m.

為了驗證該控制律的有效性,本文根據爬壁機器人一般在壁面上的爬行路徑,設計了“S”形路徑,公式如式(28)所示.

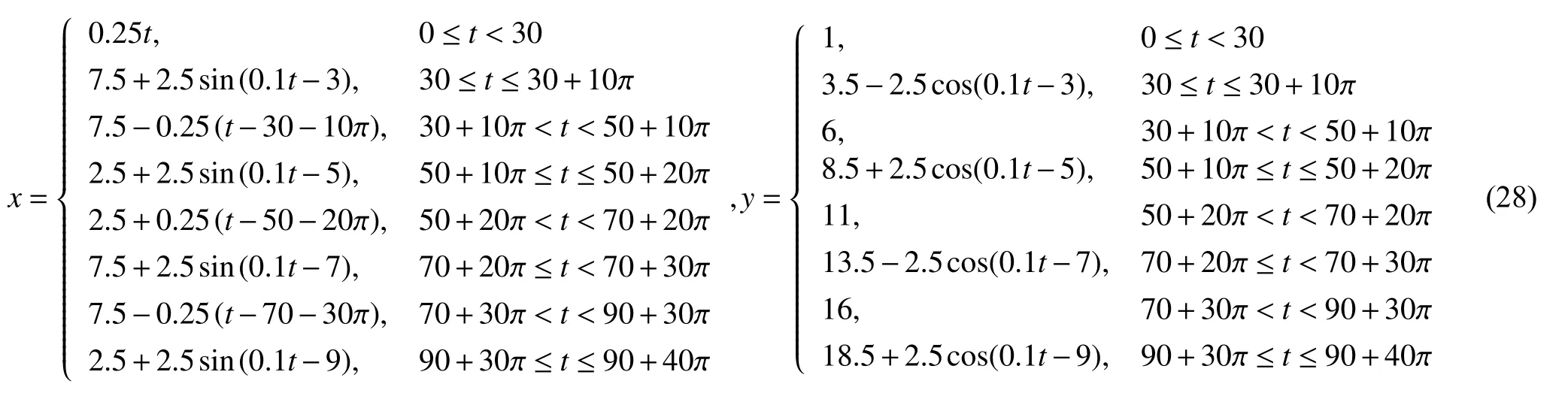
該路徑包括勻速直線運動,順時針勻速圓周運動及逆時針勻速圓周運動,初始姿態為假設外界干擾為d=5sin3(t)+e?t?cos(t),控制參數設計為:kx=0.1,ky=3,kθ=1,L0=1,L1=10,ε1=ε2=1,β=5,?=5,k1=85,k2=50,k3=1.仿真結果如圖5所示.

由圖5–圖7所示,可以觀察到雖然常規滑模控制也可以得到比較好的跟蹤效果,但常規滑模控制的誤差存在抖振,位置誤差為5 cm 左右,姿態角誤差也在?0.05°～0.05°內振蕩.相較而言,加入改進型干擾觀測器后的控制律位姿誤差趨近于0,魯棒性能更優,抗干擾效果也更好,跟蹤效果如圖8所示.

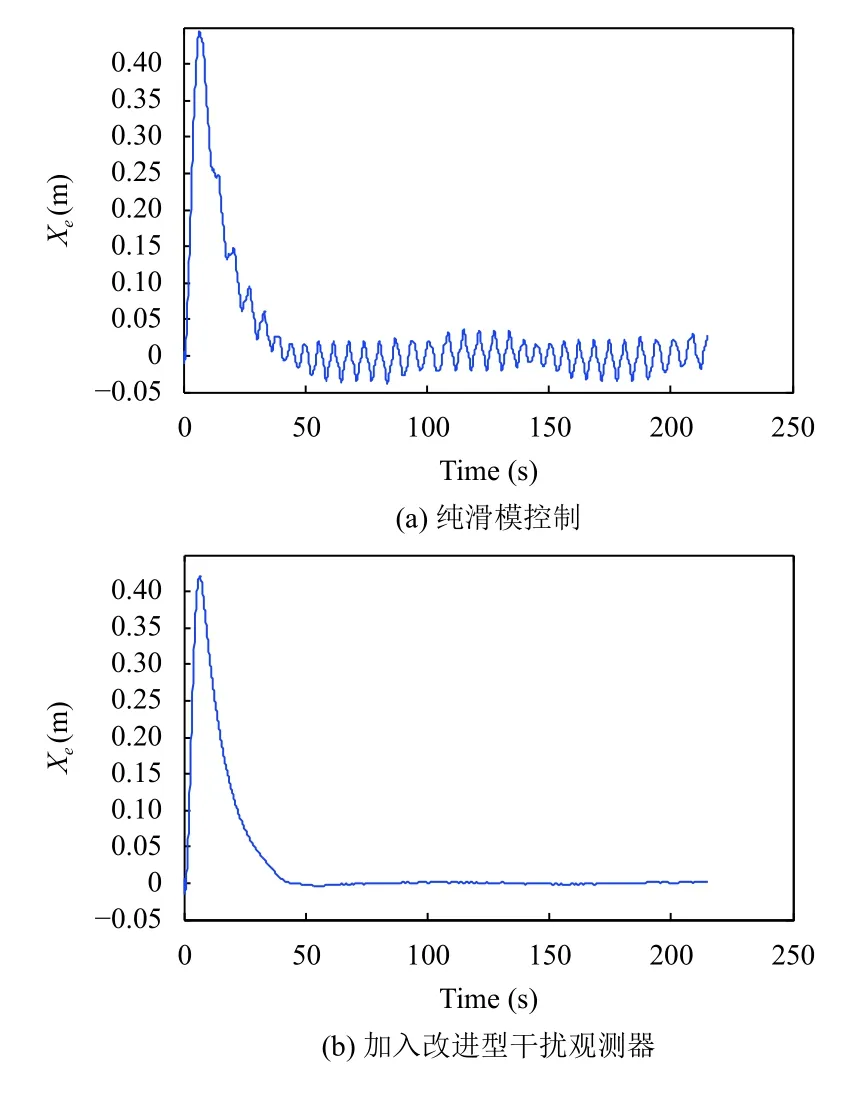
圖5 X 軸跟蹤誤差

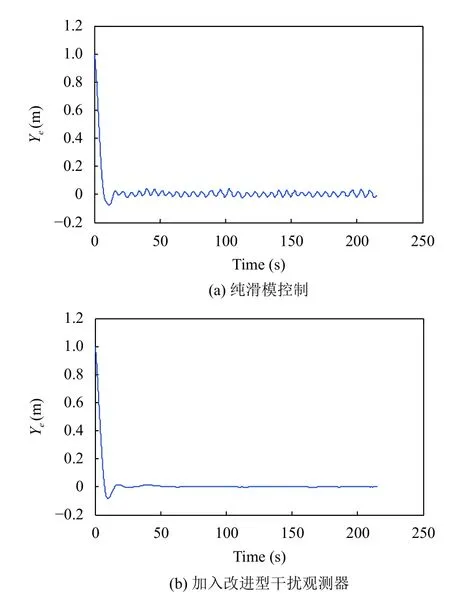
圖6 Y 軸跟蹤誤差

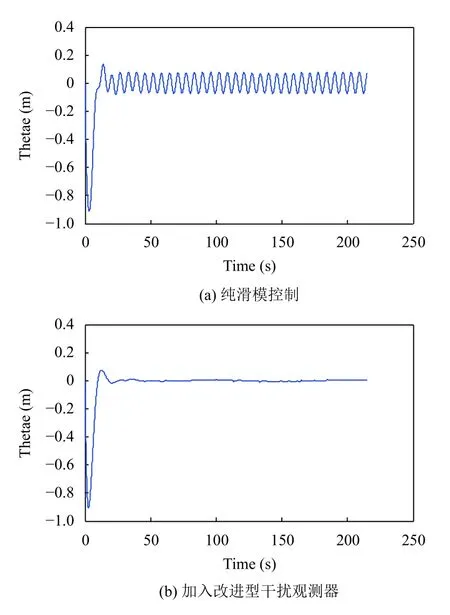
圖7 姿態角跟蹤誤差

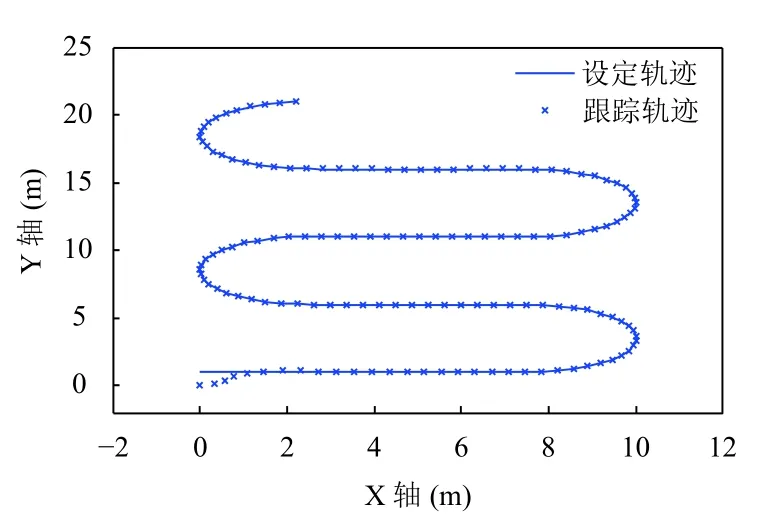
圖8 加入干擾觀測器軌跡跟蹤效果

而由圖9及圖10可知,改進型干擾觀測器基本可以擬合外界干擾,且與文獻[14]的干擾觀測器相比誤差的振蕩范圍更小,觀測效果更佳.

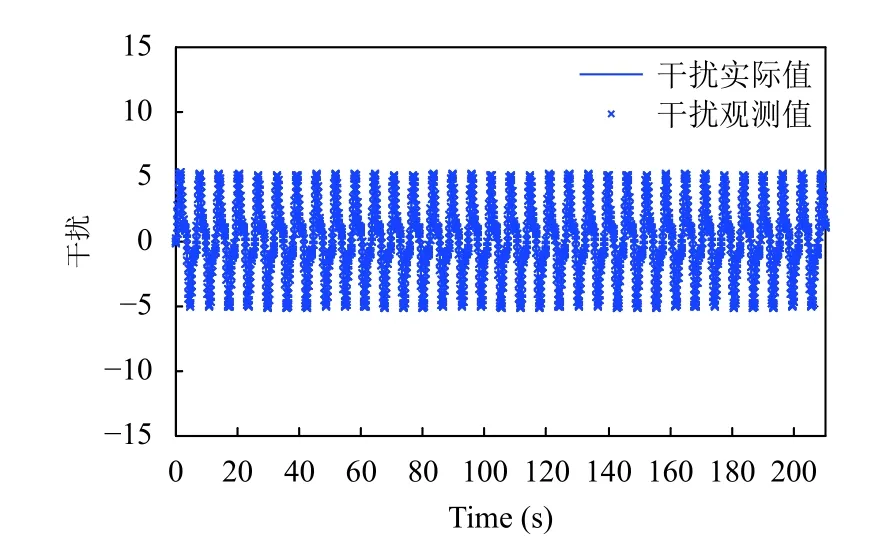
圖9 非線性干擾觀測器觀測效果

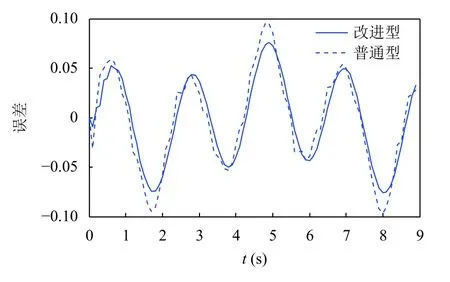
圖10 非線性干擾觀測器觀測誤差

4 結論

本文為了解決存在建模誤差和擾動未知的爬壁機器人軌跡跟蹤問題設計控制器,首先建立了爬壁機器人的運動學及動力學模型,其次引入干擾觀測器對系統建模誤差及外部干擾進行觀測,設計出一種基于改進型干擾觀測器的反演滑模控制方法.Lyapunov 函數證明了系統的穩定性,仿真結果表明了控制方案的有效性.