多尺度形態(tài)學的風電軸承故障診斷研究

田 軍,李勁濤

(1.吉林電子信息職業(yè)技術學院 電氣工程學院，吉林 132021 )

0 前言

由于近年來全球溫室效應越來越嚴重，清潔能源的使用受到人們廣泛的關注。風能是清潔、無污染的可再生能源之一。隨著我國經(jīng)濟快速發(fā)展， 國內用電量的增加，我國的風力發(fā)電機安裝量正在逐年增加。但是由于風力發(fā)電機常年服役在野外等復雜的工作環(huán)境，這給風機的安全運行維護帶來巨大難度。風力發(fā)電機的傳動系統(tǒng)承受著低速重載的作用，故其傳動系統(tǒng)經(jīng)常發(fā)生故障[1-4]。其中因軸承引發(fā)的風機事故占總事故的45%。當軸承發(fā)生局部故障時，會產(chǎn)生周期振動的沖擊信號。軸承的故障特征受到噪聲干擾而無法識別，這使軸承的故障診斷非常困難。因此如何從軸承的振動信號里提取有用的故障特征，對風機的安全維護起著至關重要的作用[5-7]。

數(shù)學形態(tài)學是一種形式簡單且計算效率高的數(shù)學方法。數(shù)學形態(tài)學早期被應用在圖像處理上，由于其優(yōu)越的濾波性能，現(xiàn)在被廣泛地應用在機械信號的信號處理上[8-11]。數(shù)學形態(tài)學由四種基本形態(tài)學算子組成，每種形態(tài)學算子能夠對信號產(chǎn)生不同的處理方式。膨脹算子能夠擴展波峰，腐蝕算子能夠擴展波谷，開算子提取負脈沖，閉算子提取正脈沖。由這四種基本形態(tài)學算子可以組合成具有濾波功能的差分算子。傳統(tǒng)的形態(tài)學采用單尺度處理信號。在處理信號的過程中由于單尺度形態(tài)學包含故障信息不完整。因此，本文在單尺度的基礎上研究多尺度形態(tài)濾波[12-14]。最終， 通過對實際風力發(fā)電機的故障信號分析，證明了該方法的有效性。

1 形態(tài)學分析

1.1 基本形態(tài)學算子

數(shù)學形態(tài)學主要由 4 種基本形態(tài)學算子組成。假設獲得的振動信號f(n)其表達形式為F=(0,1,…,n-1)， 結構元素g(m)的表達形式為G=(0,1,…,m-1) (n≥m), 則膨脹、腐蝕、開算子和閉算子分別定義如下：

(f⊕g)(n)=max[f(n-m)+g(m)]

(1)

(fΘg)(n)=min[f(n+m)-g(m)]

(2)

(3)

(f?g)(n)=(f⊕gΘg)(n)

(4)

圖1 四種基本算子性能

基于4種基本算子構建增強差分算子為EDO。

(5)

1.2 多尺度形態(tài)學分析

由于多尺度形態(tài)學比單尺度含有較豐富的故障特征信息，因此本文研究多尺度形態(tài)學的故障診斷方法。假設ε(ε=1, 2, 3, …,λ)是結構元素SE的尺度，多尺度形態(tài)學算子定義如下：

多尺度膨脹算子：

(6)

多尺度腐蝕算子：

(7)

多尺度開運算：

(8)

多尺度閉運算：

(f?λg)(n)=((f⊕λg)Θλg)(n)

(9)

則EDO算子在多尺度形態(tài)下的表達式為

(10)

2 結構元素的尺度選擇

2.1 結構元素

結構元素 SE 主要由高度、形狀和長度三部分組成。研究表明 SE 的高度和形狀對濾波結果影響較小[15]。因此，本文選擇高度為零的扁平型結構元素。SE 的長度與尺度的對應關系如表 1 所示。

表1 SE尺度與長度的對應關系

2.2 TEK評價因子

峭度是檢測沖擊信號的四階無量綱統(tǒng)計量。其表達式定義如下：

(11)

式中，E()表示數(shù)學期望；μ和σ分別表示均值和標準差。

Teager能量算子能夠跟蹤檢測信號的瞬時能量。對于離散信號x(t),其能量算子的表達式為

φ[x(t)]=[x(t)]2-x(t+1)x(t-1)

(12)

Teager 能量算子能夠同時考慮信號的瞬時頻率和幅值的影響，是一種有效的檢測沖擊信號的指標。為了最大限度提取沖擊信號，本文采用 TEK 指標進行選擇。TEK 指標[16]由峭度譜和Teager 能量算子組成，其表達式為

(13)

在通過TEK確定 MEDO 的最優(yōu)尺度后，把選則的尺度進行加權，輸出的最終信號為

(14)

其中，ωλ表示在不同尺度λ下的加權系數(shù)。

3 實驗驗證

本文提出一種風力發(fā)電機滾動軸承的故障診斷方法研究，其算法的技術路線如圖2所示。

圖2 本文算法的技術路線

實驗的測試數(shù)據(jù)來自黑龍江佳木斯的某企業(yè)風場。風機的型號為 D70 1.5MW雙饋異步發(fā)電機。測試時，風的切入速度為3 m/s，切出速度為25 m/s。發(fā)電機的轉速為1 200 r/min。發(fā)電機的額定功率為1 500 kW，實驗采用加速度傳感器收集振動信號，實驗設備的采樣頻率12 000 Hz。實驗測試裝置和傳感器的安放位置如圖3所示。

圖3 實驗測試裝置及傳感器安裝示意圖

通過圖3的加速度傳感器收集振動信號數(shù)據(jù)，測試的軸承型號及幾何參數(shù)如表2所示。通過表2計算得到風機軸承的故障頻率分別為： 內圈106.5 Hz, 外圈93.5 Hz, 保持架11.7 Hz, 滾動體190.9 Hz。測得的風機時域圖和頻域圖分別如圖4a和圖4b所示。

表2 滾動軸承的幾何參數(shù)

圖4 風機實驗信號的時域波形與頻域波形

在圖4b的頻譜中無法識別出滾動軸承有效的頻率成分，故障特征受背景噪聲干擾嚴重。對實驗信號進行包絡譜分析，分析結果如圖5所示。在圖5中可以識別到風機軸承微弱的外圈故障頻率106.9 Hz。但是外圈故障頻率的幅值較為微弱。

圖5 風機實驗信號的包絡譜

采用本文提出的方法對實驗信號進一步處理。首先應用MEDO處理實驗信號，得到的多尺度時域圖和多尺度頻域圖分別如圖6a和6b所示。從圖6b中可以發(fā)現(xiàn)，不同尺度下經(jīng)MEDO方法處理的結果不同，尺度越小故障信息越完整但是噪聲越多，相反尺度越大噪聲越小但是故障信息不完整。因此如何選擇最優(yōu)尺度對MEDO方法影響巨大。

圖6 實驗信號在多尺度下的時域圖和頻域圖

采用TEK衡量指標去選擇MEDO的最優(yōu)尺度，得到的TEK優(yōu)化曲線和在最優(yōu)尺度下最終獲得的加權結果分別如圖7a和7b所示。在7a中可以發(fā)現(xiàn)當尺度為21的時候，TEK值最大。因此MEDO的尺度加權范圍為1到21。在圖7b中，軸承外圈的故障頻率106.9 Hz、213.8 Hz以及三倍故障頻率320.7 Hz能夠清楚的被看到。并且軸承的2倍轉頻40 Hz也能清楚的看到。對比圖5和圖4b，本文提出的算法能夠更有效的識別出風機軸承的故障特征頻率。

圖7 MEDO方法處理實驗信號結果

為了進一步證明本文提出方法的優(yōu)越性，采用單尺度的EDO方法和EEMD方法[17]處理相同的實驗信號。處理結果分別如圖8和圖9所示。在圖8中，EDO方法處理實驗信號只能看到故障頻率106.9 Hz和213.8 Hz。但是從圖中可以看到213.8 Hz的軸承故障頻率受噪聲干擾嚴重。在圖9b中可以看到，經(jīng)EEMD方法處理后可以識別出106.9 Hz和213.8 Hz的軸承故障頻率。但是其故障幅值依然比較微弱。這兩種方法與本文提出MEDO方法進行對比，可以進一步表明本文提出算法的優(yōu)越性。

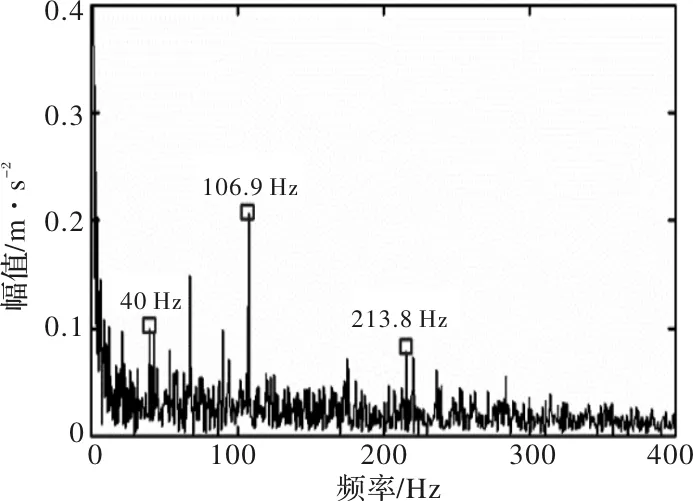
圖8 EDO 方法處理實驗信號的結果

圖9 EEMD方法處理實驗信號的結果

4 結論

為了檢測大型風力發(fā)電機滾動軸承的微弱故障，一種多尺度的MEDO形態(tài)學分析方法被提出。通過對風機實驗信號的檢測結果可以發(fā)現(xiàn)。FFT譜和包絡譜無法準確的識別出軸承故障。而MEDO方法可以有效地檢測出軸承外圈故障頻率106.9 Hz、213.8 Hz以及三倍故障頻率320.7 Hz。與EDO方法和EEMD方法的實驗對比結果表明，本文提出的方法具有優(yōu)越的滾動軸承故障特征提取能力。