無線光中繼通信在弱湍流時的性能估計方法

陳 曉，胡曉英

(上海申核能源工程技術有限公司，上海 200233)

0 引 言

自由空間光通信(Free-Space Optical Communications, FSO)運用激光視距鏈路可獲得每秒幾千兆的速率。天氣晴朗時，FSO系統的性能主要受制于湍流導致的信號衰落[1-2]。對于短距FSO信道，通常可以用對數正態分布描述其功率。對于溫度變化劇烈的環境，例如核電站內部，光通信信道也服從對數正態模型。當鏈路距離過長或存在障礙物時，可引入中繼節點來對抗湍流衰落[3]。對于強度調制/直接檢測(Intensity-modulation direct-detection, IM/DD)系統可使用放大-轉發(Amplify-and-Forward，AF)協議。

文獻[4] 提出了一種數值方法來估計AF系統的性能，但此類方法引入了物理意義不明的間接變量，無法直接揭示信道參數對整體系統性能的影響；文獻[5] 研究了FSO多跳中繼和平行中繼的性能近似表達，但無法得到閉式的AF中斷概率表達式。對此，不少文獻采用了針對對數正態變量求和的近似[5-6]，其中，Wilkinson和Fenton近似是目前應用最廣泛的兩類近似方法[7-8]。這兩類方法原理相通且運算復雜度相近，但其在不同條件下的選取準則并沒有文獻進行系統研究。

本文從原點矩的積分表達式上對比了Wilkinson和Fenton近似的特點，討論了在不同信噪比條件下的近似方法。仿真結果表明，在低信噪比情況下，Wilkinson近似的誤差小于Fenton近似；而在高信噪比情況下，Fenton近似的誤差則低于Wilkinson近似。

1 光通信中的對數正態信道模型

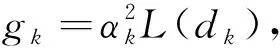
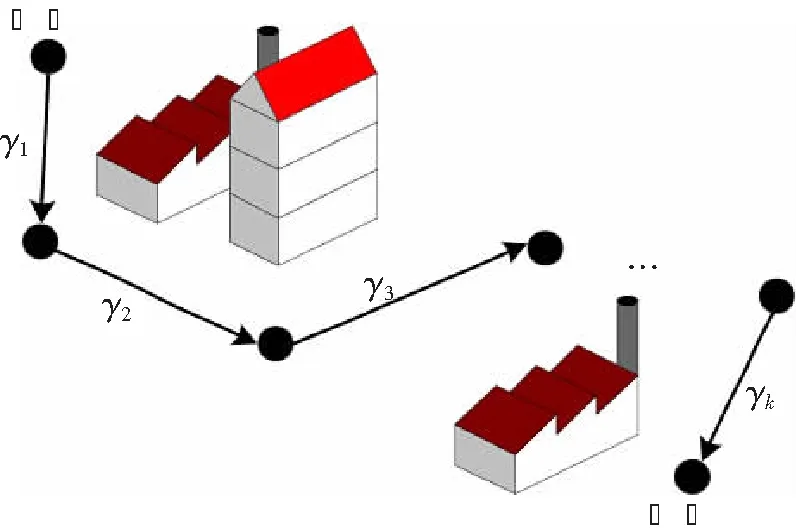
圖1 FSO多跳中繼系統

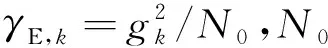
2 Wilkinson和Fenton近似

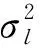
2.1 Wilkinson近似

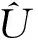
2.2 Fenton近似

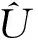
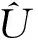
通過求解式(3)可得

2.3 Wilkinson和Fenton近似的積分表達式對比

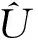
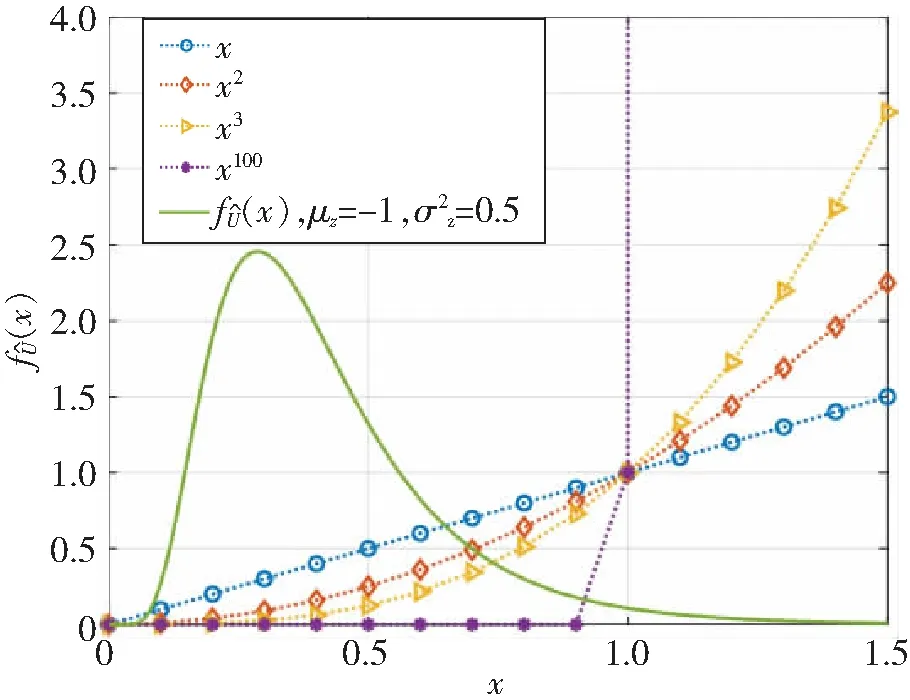
圖2 加權函數xr和概率密度函數

式中：n為求和項；Δx→0,N→。式(6)經化簡可得

上述的討論說明，由于匹配了低階矩，Wilkinson近似對于對數正態變量的和的概率密度函數具有較好的整體近似；而Fenton近似匹配了高階矩，因此更側重概率密度函數在x?1處的近似。該結論將為這兩類近似在性能分析中的應用提供準則。

3 Wilkinson和Fenton近似在多跳中繼系統中的應用

3.1 近似信宿處的信噪比

根據文獻[4] ，K跳AF網絡在信宿處的精確信噪比可表示為

式中，γk為第k條鏈路的瞬時隨機信噪比。通過展開，可將式(8)表示為

式中：γE,D為最終節點處經過光-電轉換后的電信號信噪比；γE,k為第k跳接收機處的電信號信噪比；o為高階無窮小項。假設γk→,?k=1,…,K。根據對數正態變量的性質可知，如果γE,k服從對數正態分布，則也服從對數正態分布，只是對應的μE,k參數需要取相反數。因此如果忽略式(9)中的高階小量，則可以用Wilkinson或Fenton近似來近似

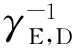
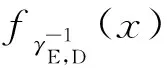
3.2 誤碼率和中斷概率近似公式

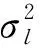
對于FSO多跳AF網絡來說，精確的誤符號率可通過如下公式計算[14]：

式中：a和b均為固定常數，取決于采用的調制方式；Q(x)為高斯積分函數，在Matlab和Mathematica等軟件工具中均為內置函數。例如，當采用二進制相移鍵控(Binary Phase Shift Keying，BPSK)時，a=1，b=2，式(11)的積分不可化簡，且fγE,D(r)的表達式包含K重無法化簡的積分。因此，即便利用數值積分方法，式(11)依然是低效且開銷巨大的。

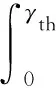
4 仿真結果

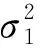
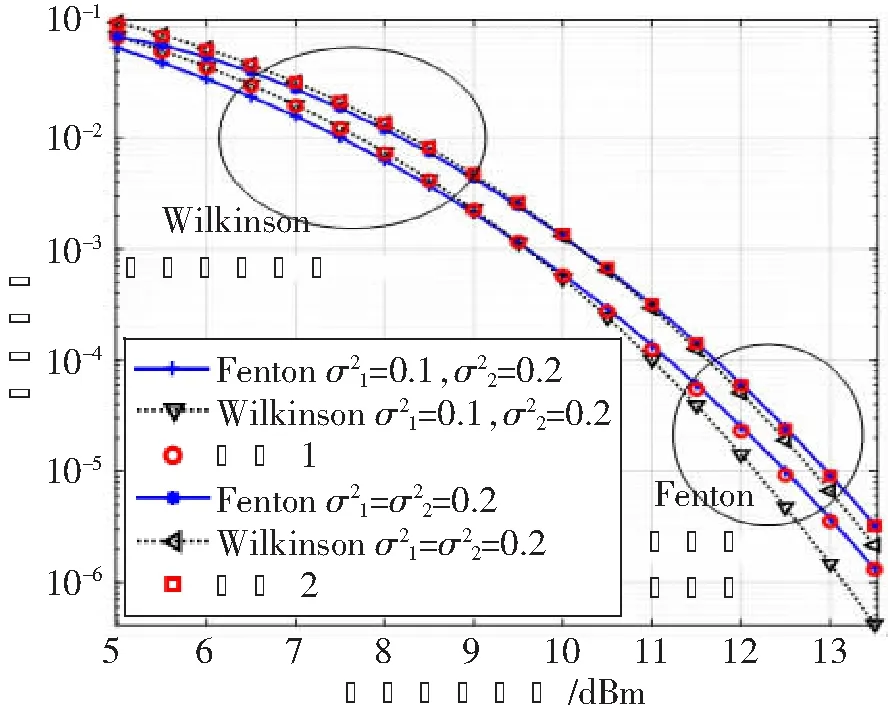
圖3 通過Wilkinson和Fenton近似得到的AF多跳系統誤符號率

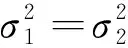
圖3和圖4共同指出，盡管Wilkinson和Fenton近似都是通過匹配原點矩來對對數正態變量的求和作近似，但由于所取得原點矩階數不同，因此其適用范圍不同。對于FSO AF中繼系統來說，在估計中低信噪比情況下的性能時應采用Wilkinson近似；而在估計高信噪比情況下的性能時應采用Fenton近似。

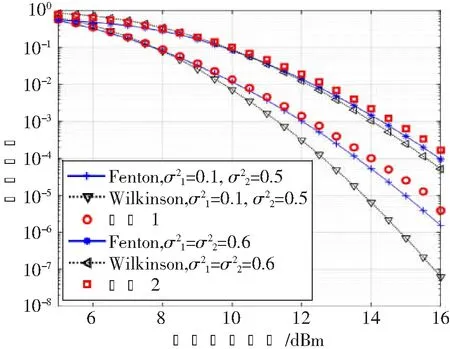
圖4 通過Wilkinson和Fenton近似得到的AF多跳系統中斷概率

5 結束語

本文對比了Wilkinson和Fenton算法用于近似對數正態和時的引入誤差。通過分析不同階的原點矩匹配公式，得出了Wilkinson方法能夠更好地近似概率密度函數的整體形狀，而Fenton方法能夠更好地近似概率密度函數的右端，即大值部分。在此基礎上，得出了AF中繼通信系統的近似誤符號率和近似中斷概率的公式，并指出高信噪比情況下應當采用Fenton近似，而中低信噪比情況下應當采用Wilkinson近似。本文方法回避了復雜的多重積分估計和蒙特卡洛仿真，為無線光中繼系統的設計提供了理論工具。