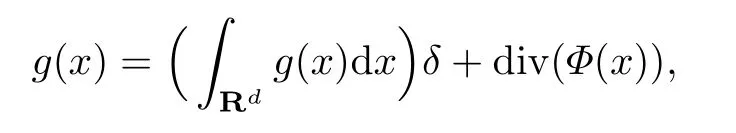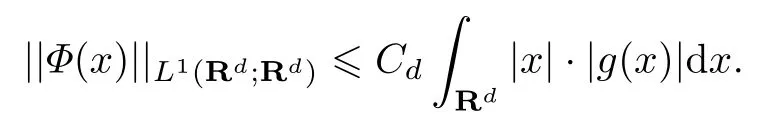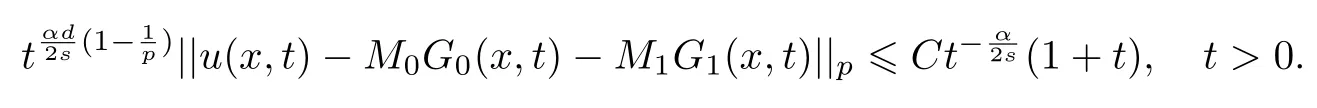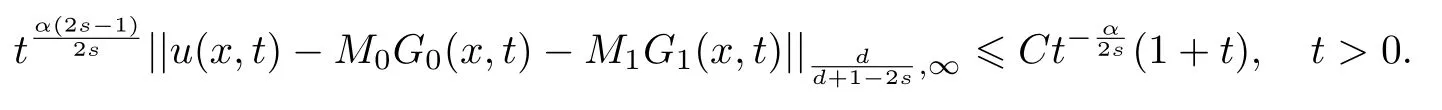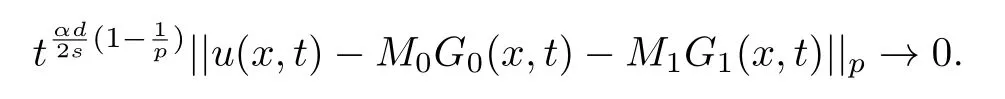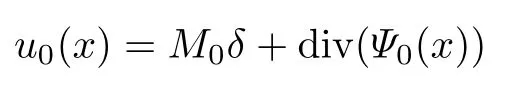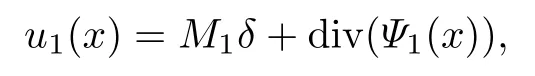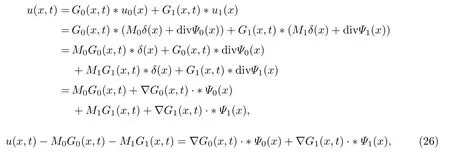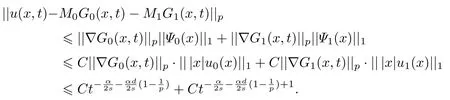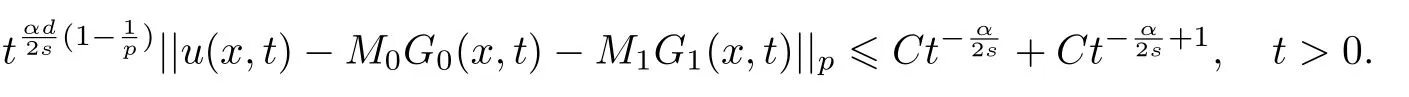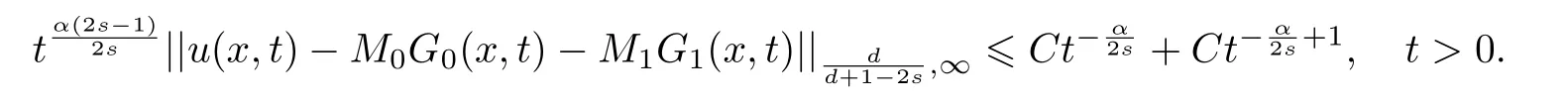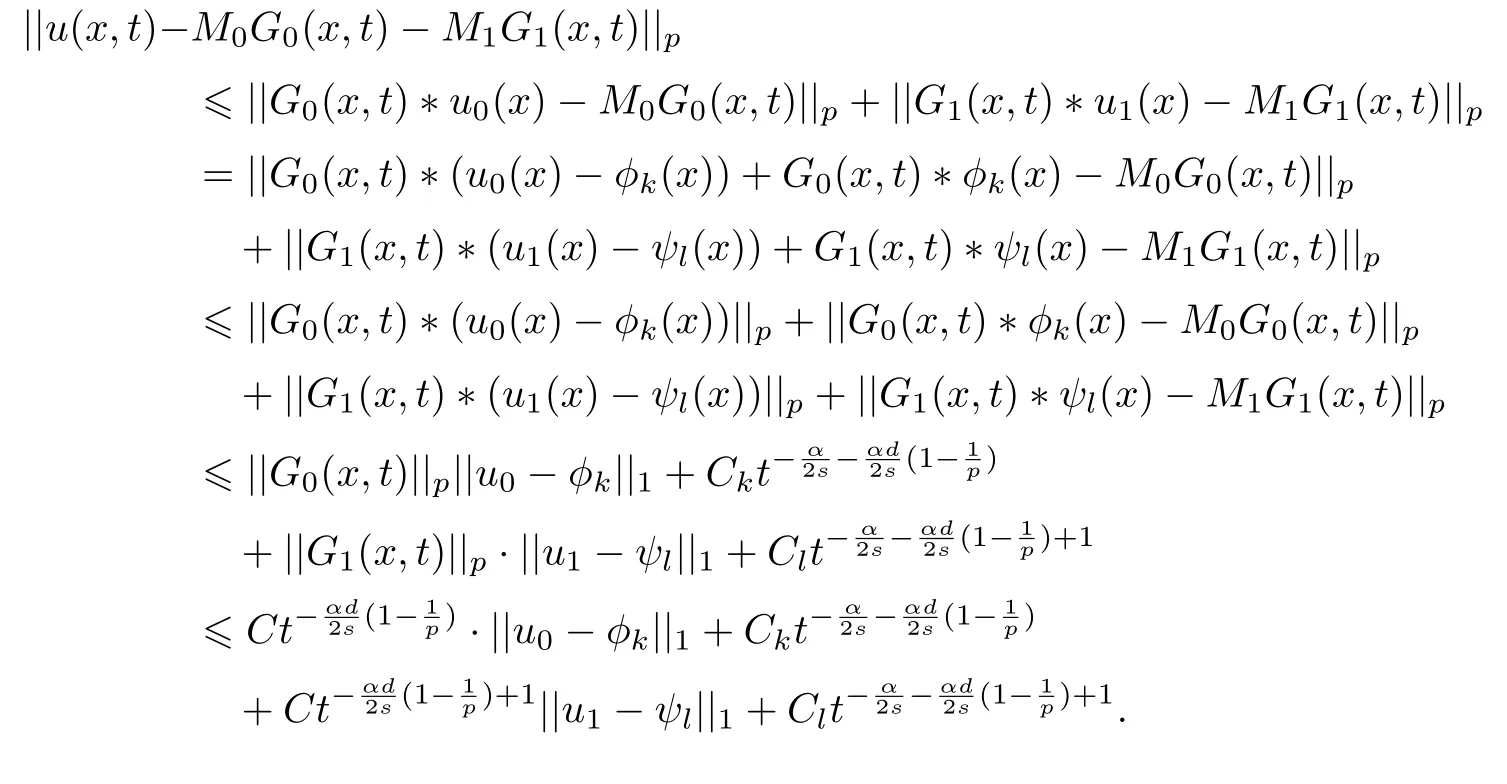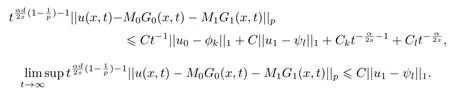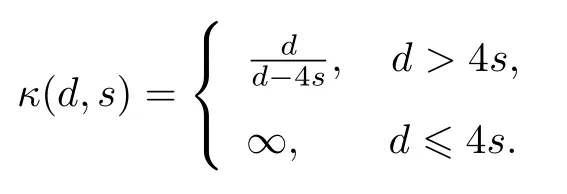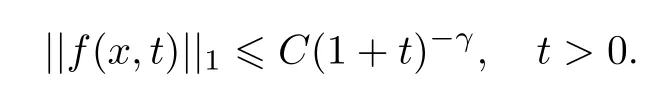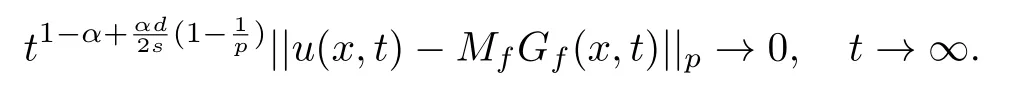時空分數階波方程解的漸近性與長時間行為
李志強
(1.上海大學理學院, 上海 200444;2.呂梁學院數學系, 山西呂梁 033001)
近幾十年來, 分數階微積分在科學與工程技術的各個領域獲得了廣泛的應用, 分數階(偏)微分方程的理論研究也得到極大發展[1-4].本工作研究時間-空間分數階偏微分方程
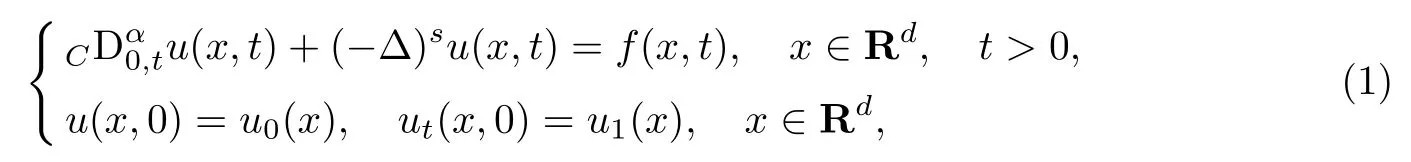
式中:表示α階Caputo 導數算子,α ∈(1,2);(??)s表示分數階Laplace 算子,s ∈(0,1);初值u0(x)、u1(x)和源項f(x,t)是已知函數;d ∈N.
函數f(t)(t>0)的α階Caputo 導數[2]定義為
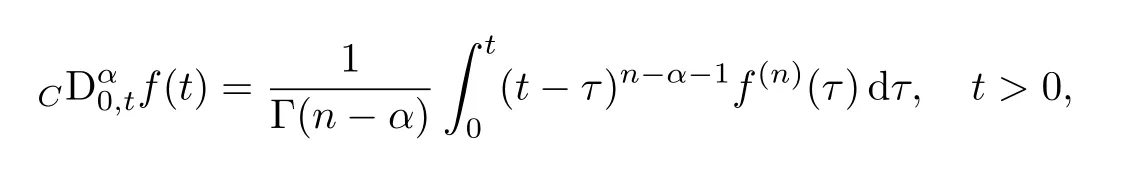
式中:n ?1<α 對于給定的函數v(x)(x ∈Rd), 積分形式的分數階Laplace[5]定義為 式中: P.V.表示積分取主值; 2013 年Ma 等[6]研究了時間分數階偏微分方程解的漸近性態, 其中時間分數階導數是在Caputo 和Riemann-Liouville 意義下的, 其導數階滿足0<α <1 或1<α <2, 而空間方向是標準的Laplace 算子.隨后, Kemppainen 等[7-8]拓展了已有結果, 并進一步討論了帶有分數階Laplace 算子的時間-空間分數階擴散方程解的漸近行為, 其中時間導數是α(0<α <1)階的Caputo 導數.最近, Li 等[9]研究了時空分數階偏微分方程, 其中時間導數是Caputo-Hadamard 分數階導數, 空間導數是分數階Laplacian.Djida 等[10]探討了時間-空間分數階偏微分方程解的估計等.本工作主要研究時間-空間分數階偏微分方程解的梯度估計和長時間行為. FoxH-函數[2,11-12]是一類重要的特殊函數, 可以用來表示方程(1)的基本解. 令m、n、μ、ν是整數且滿足0 ≤m≤ν和0 ≤n≤μ.對于al,bj ∈C 和αl,βj ∈R+(l=1,2,··· ,μ;j=1,2,··· ,ν), FoxH-函數(z)定義為 式中: 且極點 和 不重合, 即 L表示Mellin-Barnes 圍道積分曲線;極點τ=bjσ和極點τ=alk分別位于曲線L左右兩邊. H-函數具有以下兩個簡單的性質: (1) 如果存在l(l=n+1,n+2,··· ,μ)和j(j=1,2,··· ,m)使得al=bj, 那么有 (2) 令ζ,c ∈C,θ >0,k ∈N0=N∪{0}, 則H-函數有下列微分公式 接下來給出H-函數在無窮遠處和零點的漸近展開.令 引理1[11]假設式(6)成立且式(5)表示的極點是簡單極點.如果a?>0,z ?=0且則H-函數的冪級數展開式為 式中: 引理2[11]假設引理1 的條件成立, 則有 其中系數hl=hlk(k=0),hlk見引理1. 引理3[8]假設式(6)成立且滿足a?>0,z ?=0 和|argz|<, 那么有 式中: ∑′表示Gamma 函數在bj0(j=1,2,··· ,m)處對所有簡單極點的求和;∑′′是Gamma 函數在bj0(j=1,2,··· ,m)處對所有階極點的求和. 令X是測度空間,ω是X上的正測度.對于0 為弱Lp(X,ω)空間, 其中和df(γ) =ω({x ∈X:|f(x)| >γ})表示f的分布函數.弱Lp(X,ω)空間的Young 不等式[13]如下: (1) 設1 ≤p, q, r≤∞滿足則有 (2) 設1 ≤p<∞, 1 (3) 設1 文獻[10]已經給出了方程(1)解的表達式并討論了解的漸近行為, 因此本工作討論解的梯度估計.首先, 研究基本解在Lp(Rd)或弱Lp(Rd)范數意義下的估計;然后, 在初值和源項分別等于0 的情形下, 利用Young 不等式得到解的梯度估計. 方程(1)的解[10]為 式中: “?”表示空間卷積;“?”表示時間和空間同時進行卷積. 由于基本解用H-函數表達, 利用前述H-函數的性質和引理, 可求得基本解的梯度估計.令R=t?α|x|2s, 首先考慮基本解G0(x,t)的估計. 定理1已知d ∈N, 1<α<2, 0 證明 由式(8)可知 從而有 此時a?=2?α>0. 現在證明式(16).當R>1 時, 由引理1 和2 可得 因為 所以 且有 于是存在常數M(?1)使得 結合式(19)和(20), 可得 下面證明式(17). 當d>2s時, 因為b10=?1是簡單極點, 故由引理3 可知 因此, 存在常數δ0(0<δ0?1)使得 結合式(21)和(22), 可知 當d=2s時, 由式(7)和(18)可知 因為b10=?1和b20=?2是簡單極點, 由引理3 可以得出 同理, 可得 當d<2s時, 因為b10=?1 和是兩個簡單極點, 但 再次利用引理3, 可得 于是有 成立.進一步可以得到 綜合式(23)、(24)和(25)可知 定理證畢. 類似地, 可以證明下述定理. 定理2已知d ∈N, 1<α<2, 0 定理3已知d ∈N, 1<α <2, 0 (1) 如果R>1, 則有 (2) 如果R≤1, 則有 下面給出基本解G0(x,t)、G1(x,t)和Gf(x,t) 在Lp(Rd)和Lp,∞(Rd)意義下的梯度估計, 其證明方法可參考文獻[7-8], 故證明略. 為方便,記| 定理4已知d ∈N, 1<α<2, 0 定理5已知d ∈N, 1<α<2, 0 定理6已知d ∈N, 1<α<2, 0 (1) 設1 ≤p<λ(d,s), 則對任意的t>0, 有?Gf(x,t)∈Lp(Rd;Rd)且滿足估計 (2) 如果p=λ(d,s)和d+2>4s, 那么且成立不等式 注:若d+2<4s, 由定理3 可知, 對任意的t>0,?Gf(·,t)∈L∞(Rd;Rd) 且滿足 當源項f ≡0 時, 下面給出方程(1)解的梯度估計. 定理7已知d ∈N, 1<α <2, 0 (i) 如果1 (ii) 如果u0(x), u1(x)∈L1(Rd), 那么有 對于(ii), 同樣利用弱類Young 不等式(式(10))、定理4 和5, 可得 定理證畢. 在初值u0和u1恒等于0 的情況下,當源項f滿足一定條件時, 同樣可以得到解的漸近行為. 定理8已知d ∈N,1<α <2,0 那么對任意的t>0, 解u(x,t)=Gf(x,t)?f(x,t) 有估計式 證明略. 引理4[6]設g(x)∈L1(Rd)滿足∫Rd|x|·|g(x)|dx<∞.則存在Φ(x)∈L1(Rd;Rd)使得 其中δ是Dirac-Delta 函數, div(Φ(x)) 表示函數Φ(x)的散度且有 下面討論源項f ≡0 時解的長時間行為. 定理9已知d ∈N,1<α <2,0 (1) 若|||x|u0(x)||1<∞和|||x|u1(x)||1<∞, 那么有 (2) 當t →∞時, 有 證明 (1) 由條件u0(x)∈L1(Rd),|||x|u0(x)||1<∞和引理4, 存在函數Ψ0(x)∈L1(Rd;Rd), 使得 成立, 其中Ψ0(x)滿足||Ψ0(x)||1≤C|||x|u0(x)||1. 同理, 存在函數Ψ1(x)∈L1(Rd;Rd)使得 成立, 其中||Ψ1(x)||1≤C|||x|u1(x)||1.于是, 可得 式中:·?表示向量函數的卷積, 即 故有 (2) 選取序列{?k(x)(Rd) 使得并且滿足在L1(Rd)范數意義下?k(x)→u0(x).類似地, 可取序列{ψl(x)(Rd) 使得Rd ψl(x)dx=M1(l=1,2,···)且在L1(Rd)中ψl(x)→u1(x).由式(9)、定理(1)和文獻[10]中的引理4.4和4.5, 對于任意的k、l, 可得 因此, 令l →∞, 定理得證. 最后考察初值u0=u1≡0 時方程(1)的解在t →∞時的情況.為方便起見, 記 定理10已知d ∈N,1<α<2,0 如果1 ≤p≤∞(d<4s)或者1 ≤p<κ(d,s)(d≥4s), 那么對于u(x,t)=Gf(x,t)?f(x,t)成立 證明略. 致謝上海大學李常品教授對本工作提出了寶貴的意見, 在此致以衷心的感謝!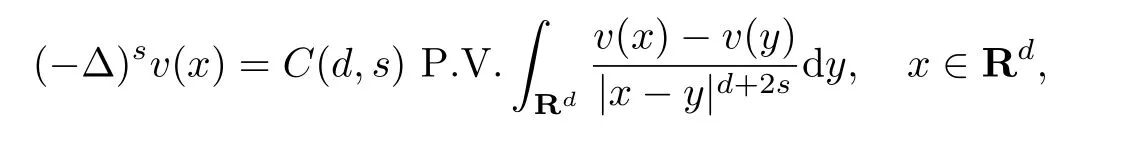
1 預備知識
1.1 Fox H-函數的定義與性質
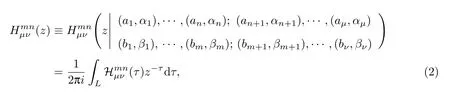
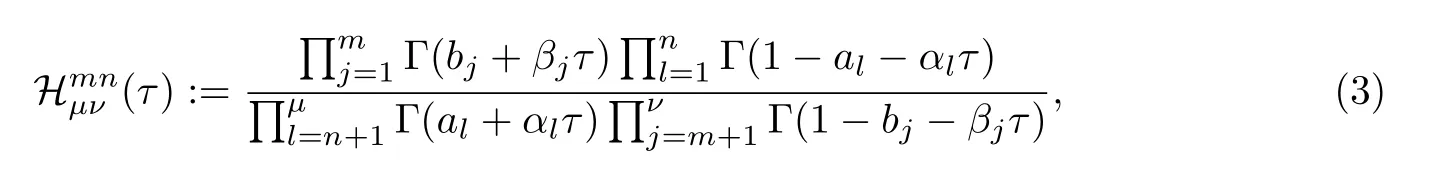
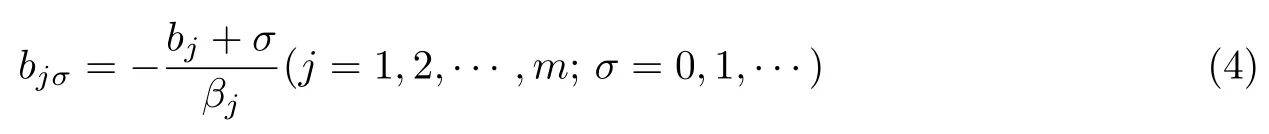
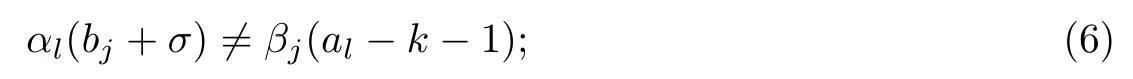
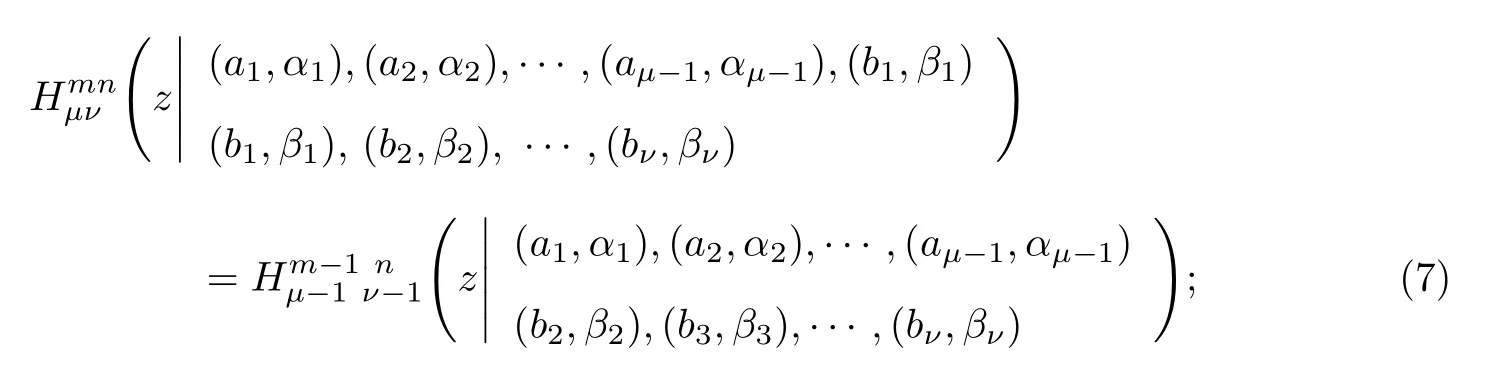
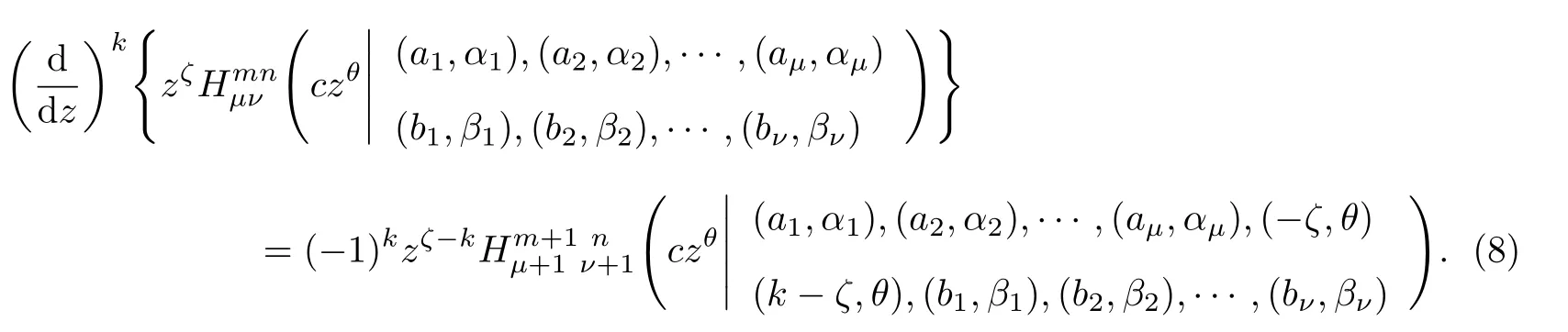

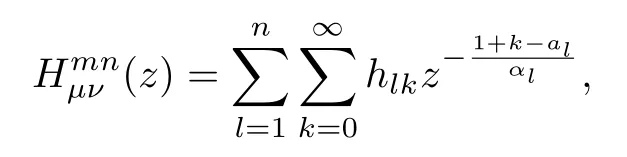
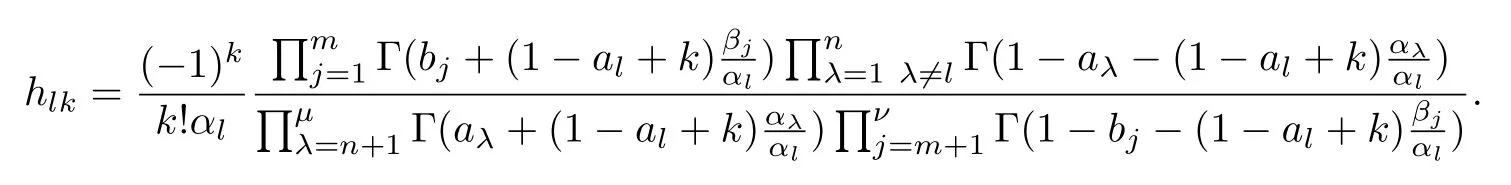
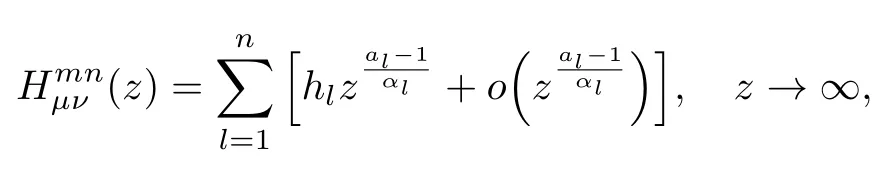
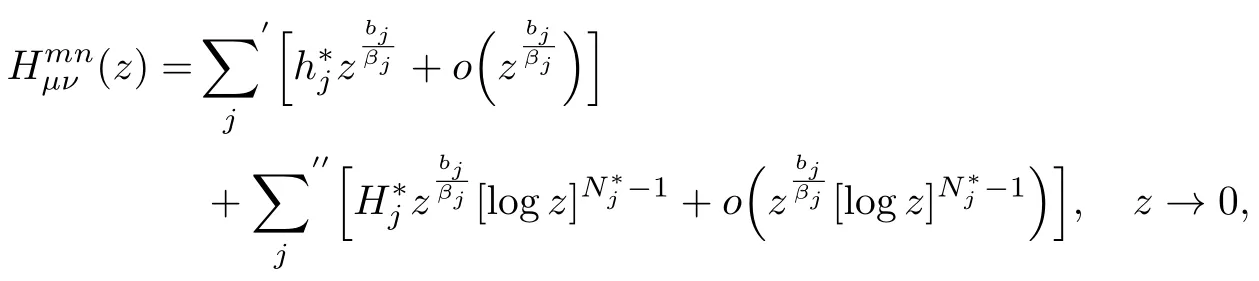
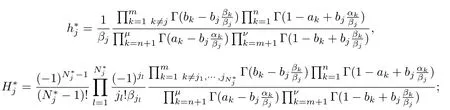
1.2 Lp 空間和Young 不等式
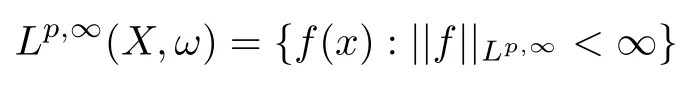
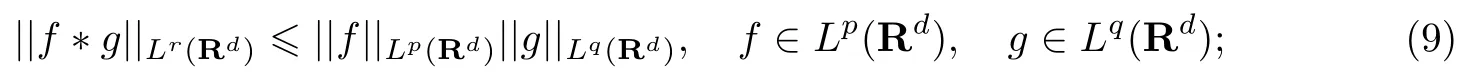
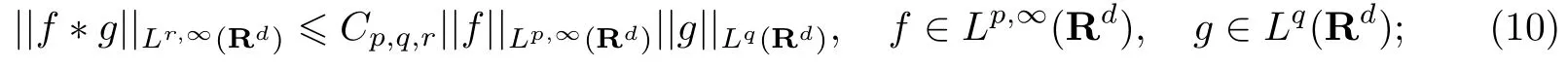
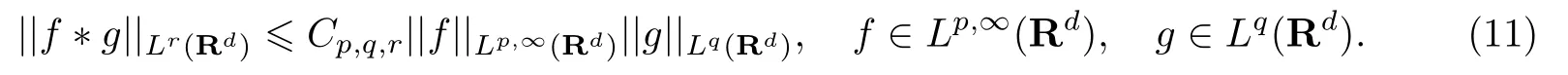
2 解的梯度估計
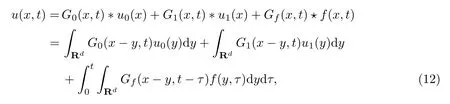
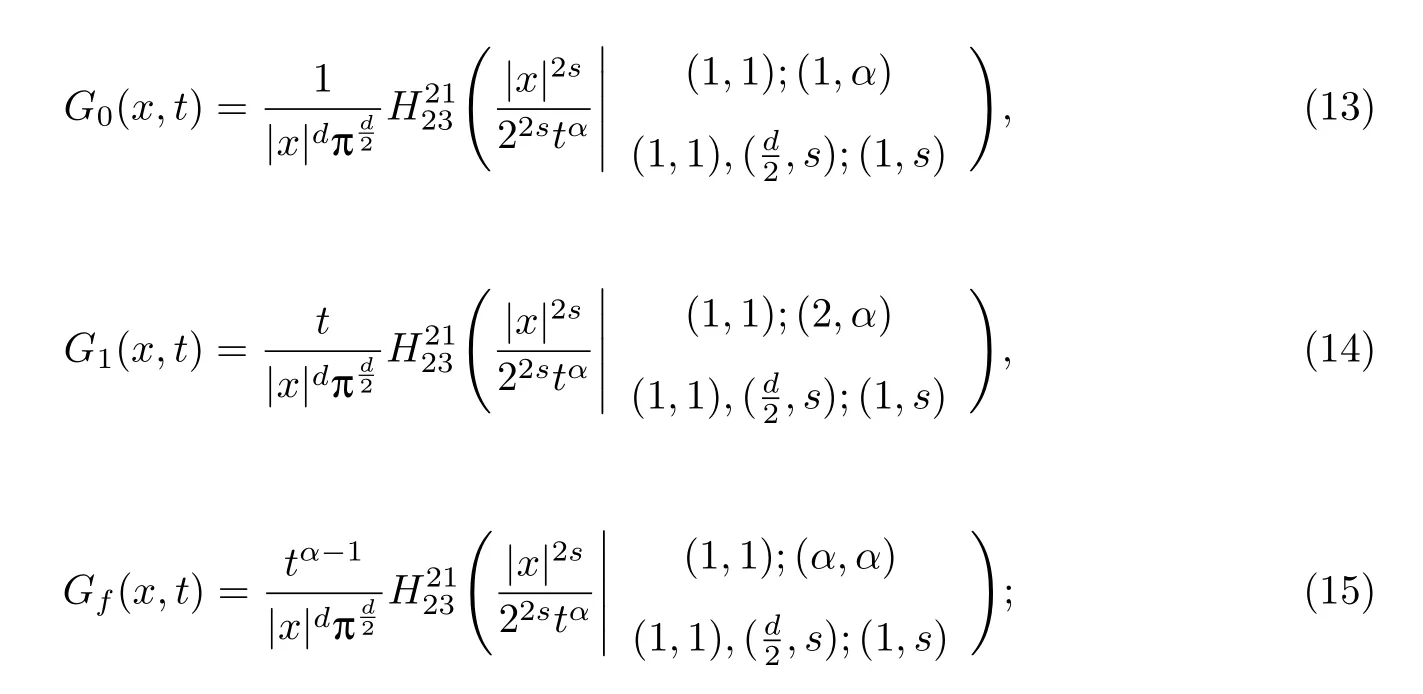
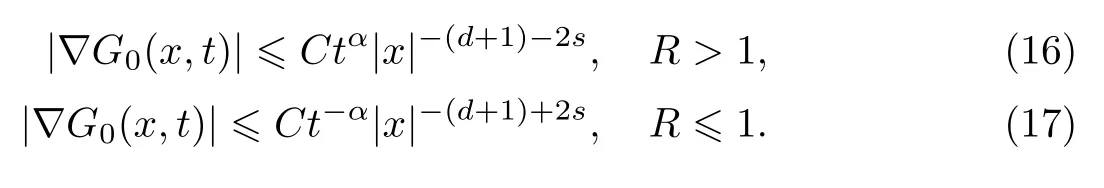
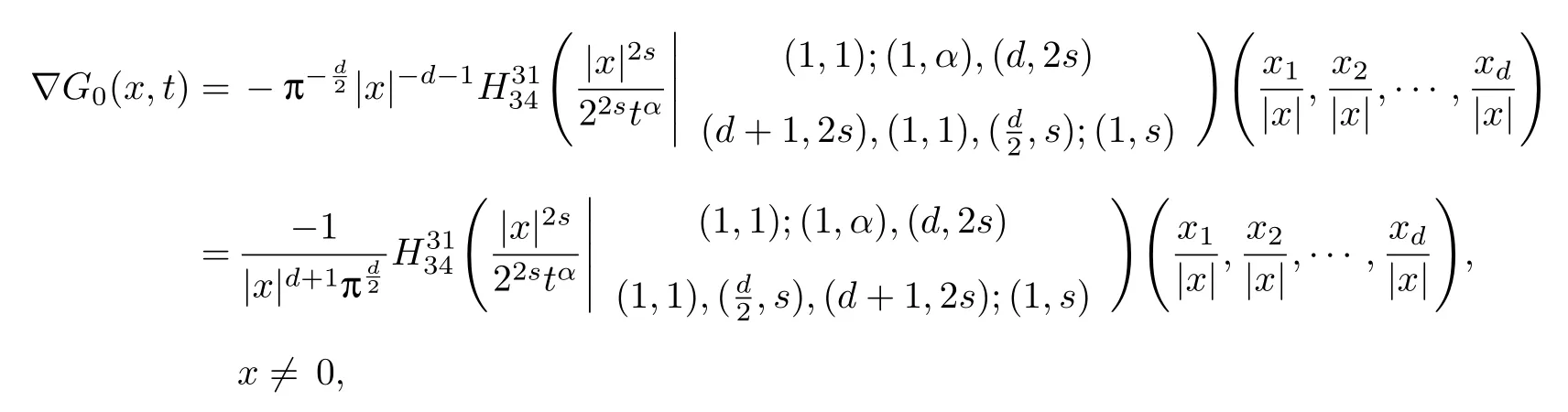
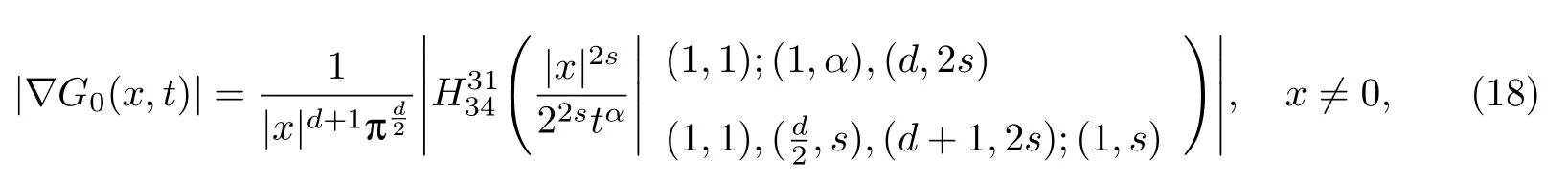
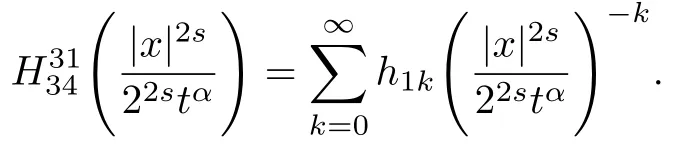
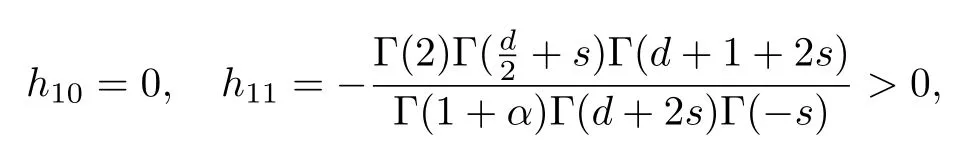
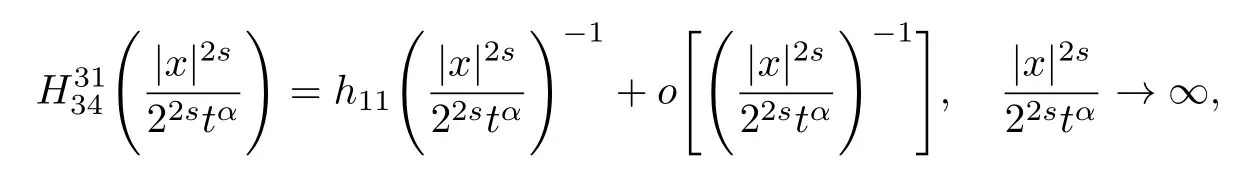
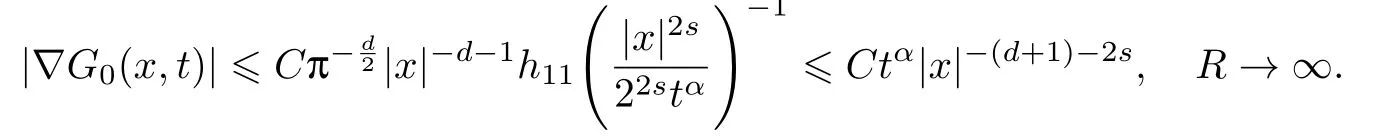
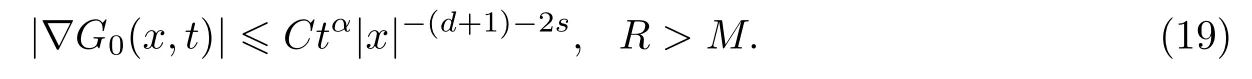
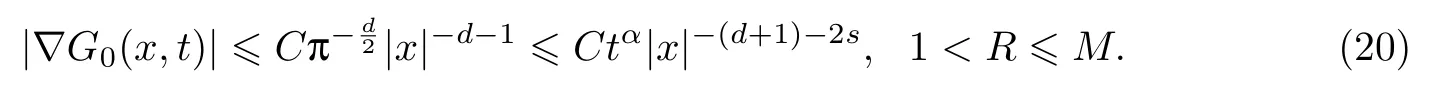

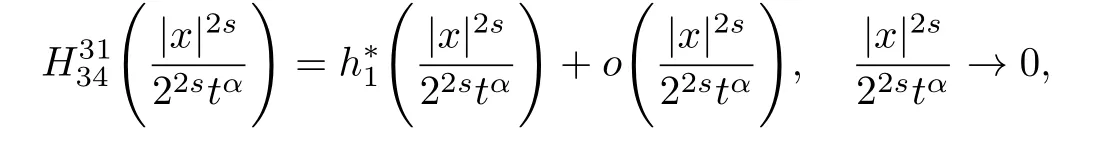
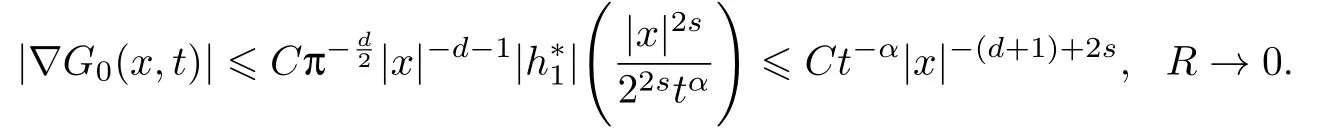
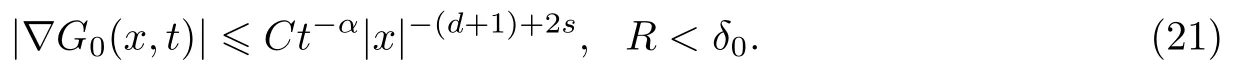
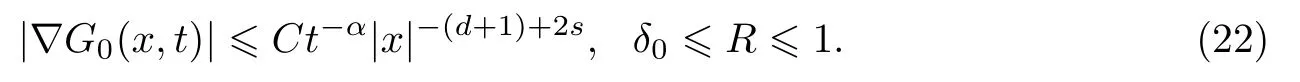
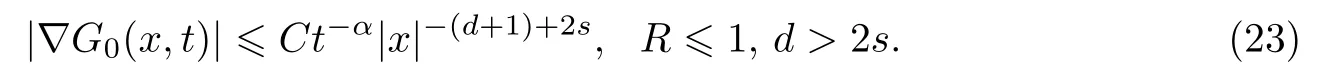
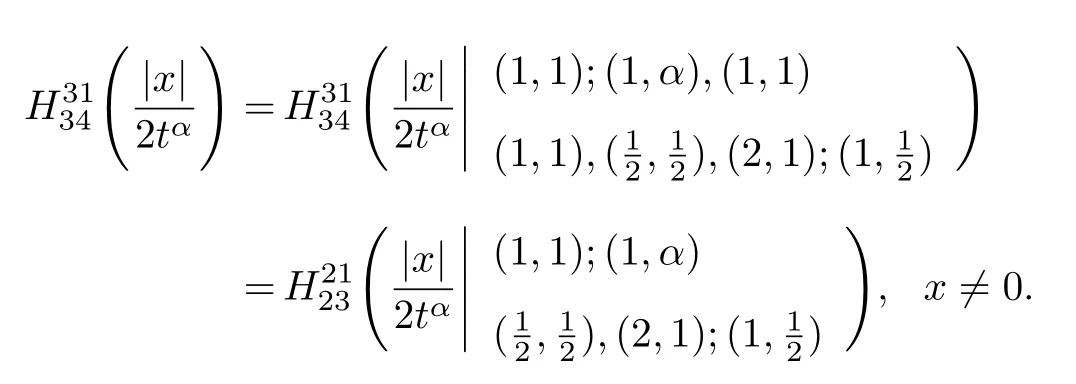
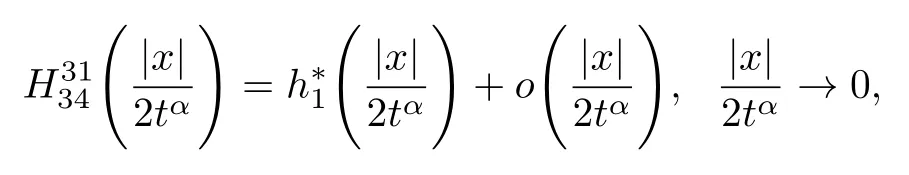

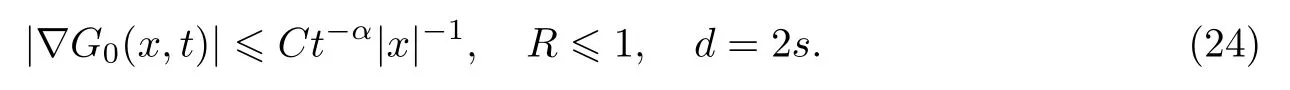
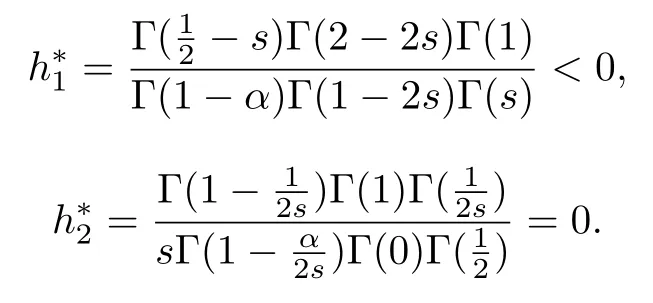
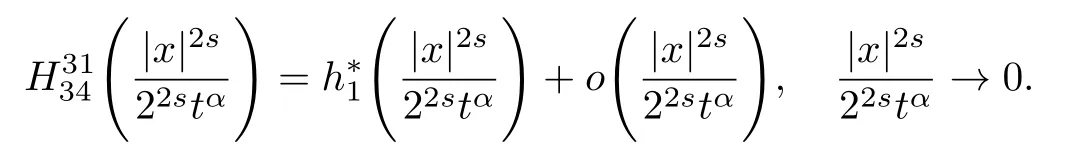
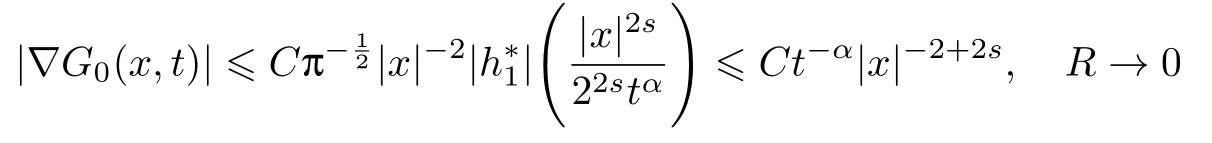
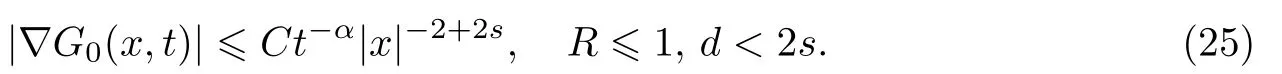
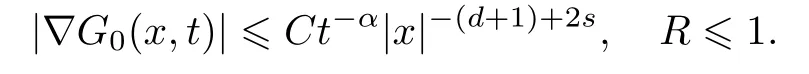
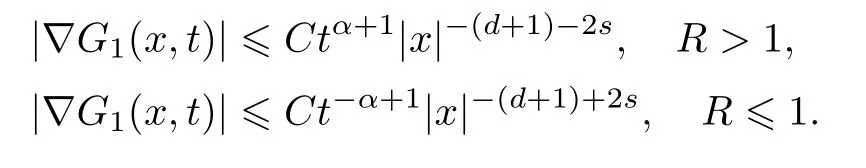
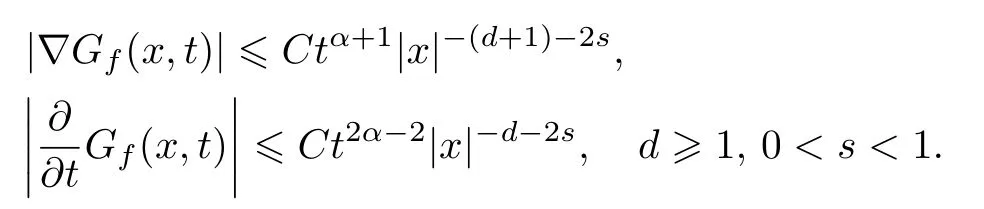
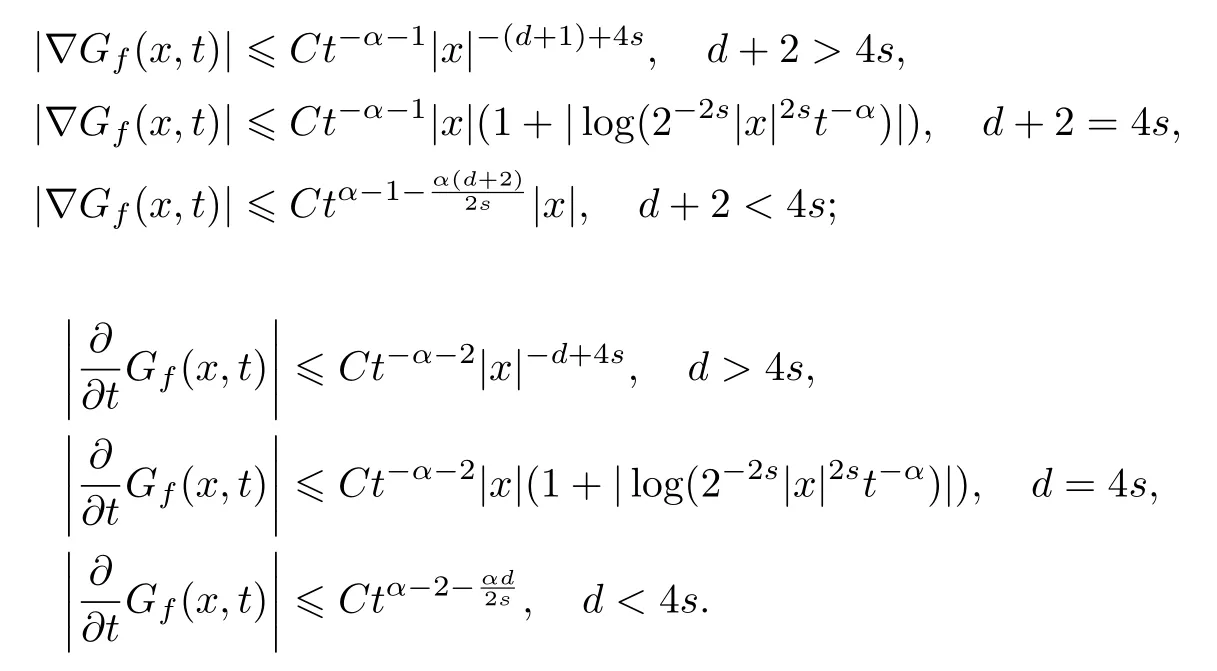
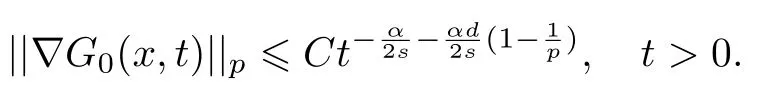
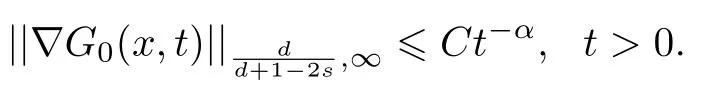
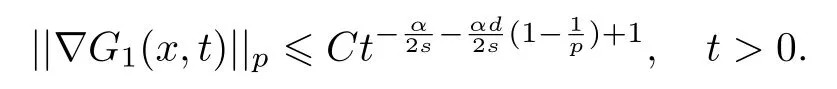
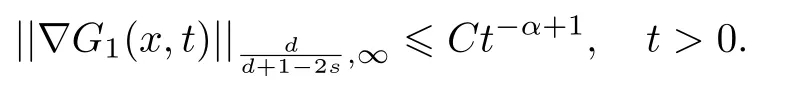
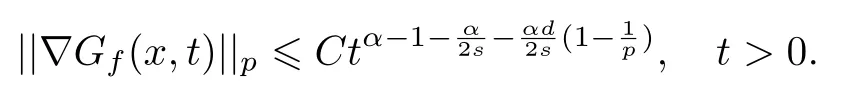
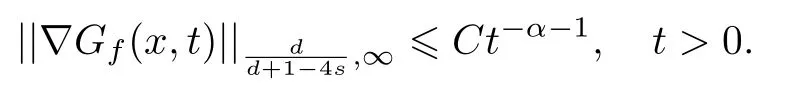
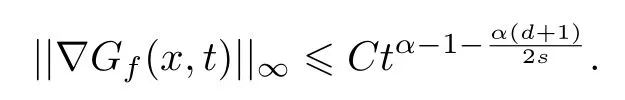
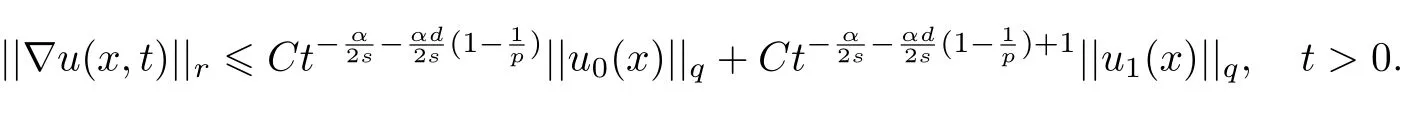
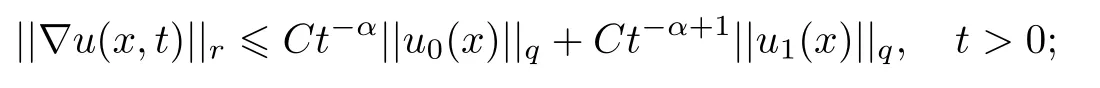
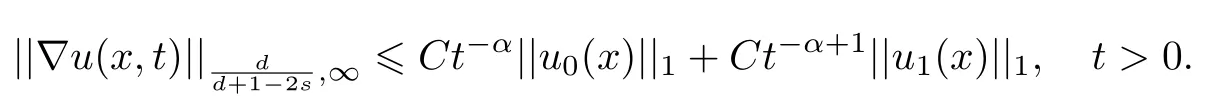
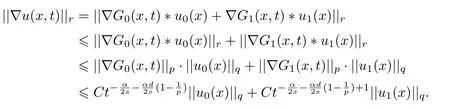
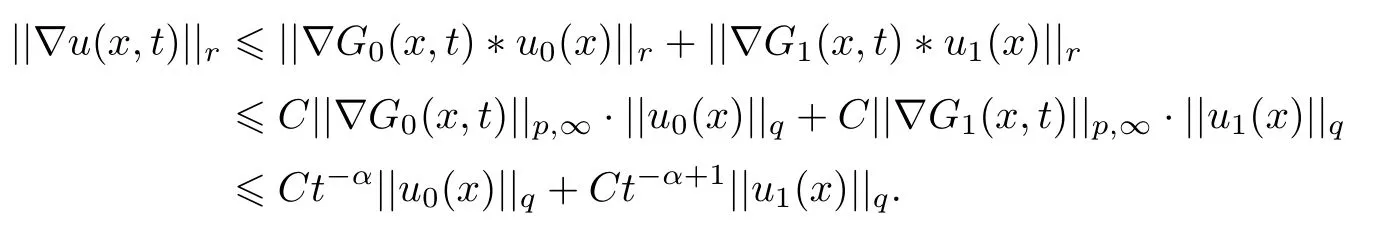
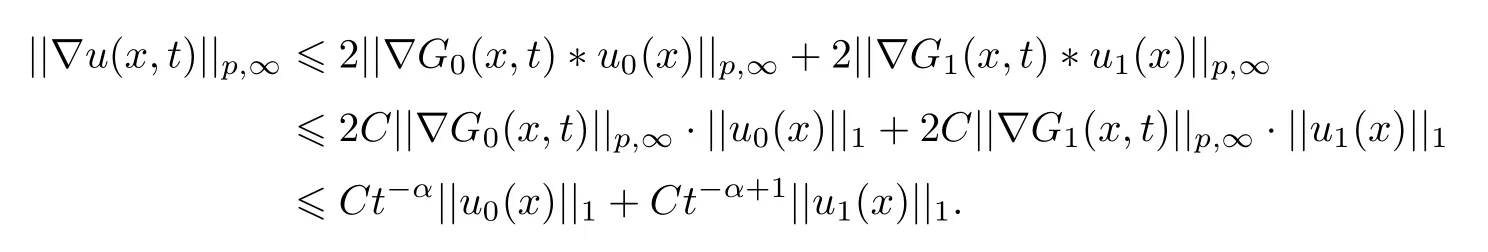
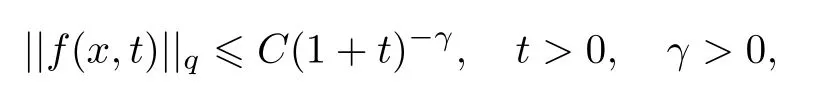
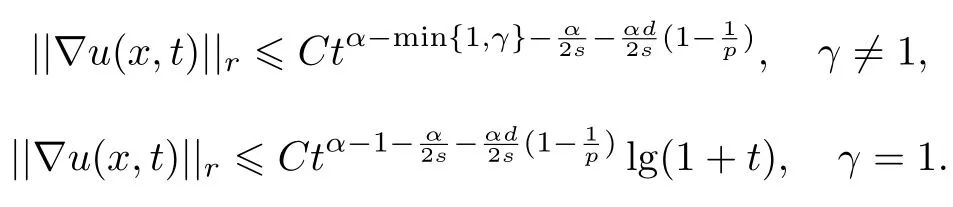
3 解的長時間行為