線性周期快速切換系統(tǒng)的平衡截?cái)嗄Ｐ徒惦A

杜 鑫, 胡 正, 王建英

(1.上海大學(xué)機(jī)電工程與自動(dòng)化學(xué)院, 上海 200444; 2.上海大學(xué)計(jì)算中心, 上海 200444)

許多工程實(shí)際中的系統(tǒng)通過(guò)機(jī)理建模通常會(huì)導(dǎo)致復(fù)雜的高階數(shù)學(xué)模型, 而直接使用這些高階模型通常會(huì)給后續(xù)系統(tǒng)仿真、分析、綜合帶來(lái)數(shù)值計(jì)算及物理實(shí)現(xiàn)上的困難, 因此需要通過(guò)模型降階方法來(lái)生成一個(gè)與原始系統(tǒng)具有相似響應(yīng)特性的低復(fù)雜度的降階模型[1-3].在控制理論、計(jì)算數(shù)學(xué)等領(lǐng)域中被廣泛接受的模型降階方法包括平衡截?cái)喾╗4]、矩匹配法(Krylov 子空間法)[5]、本征正交分解[6].起源于控制系統(tǒng)主元分析的平衡截?cái)喾ㄓ捎谄渌惴ê?jiǎn)潔, 同時(shí)可以給出合理的先驗(yàn)誤差上界, 被視為解決線性時(shí)不變系統(tǒng)以及諸多含有復(fù)雜動(dòng)態(tài)特性的類線性系統(tǒng)模型降階問(wèn)題的一個(gè)較好的理論框架.

切換系統(tǒng)是指由一組連續(xù)或離散動(dòng)態(tài)子系統(tǒng)組成, 并按某種切換律在各子系統(tǒng)間切換的動(dòng)力系統(tǒng), 許多工程系統(tǒng)如電力電子系統(tǒng)、輸電系統(tǒng)、飛行器控制系統(tǒng)、機(jī)器人控制系統(tǒng)等,都需要采用切換系統(tǒng)模型來(lái)描述其固有的動(dòng)態(tài)特性.切換系統(tǒng)在過(guò)去30 多年間一直是控制與系統(tǒng)領(lǐng)域的研究熱點(diǎn)之一[7-10].近年來(lái)切換系統(tǒng)的模型降階問(wèn)題得到了許多學(xué)者的關(guān)注, 并涌現(xiàn)出了一系列相關(guān)成果[11-28], 其中絕大多數(shù)工作都與平衡截?cái)喾ㄖ苯踊蜷g接相關(guān).Petreczky等[14-15]借助線性矩陣不等式定義并求解共同可控/可觀格拉姆矩陣, 進(jìn)而給出可生成與線性時(shí)不變系統(tǒng)情形下相同形式誤差界的平衡截?cái)嗨惴? Shaker 等[16-17]在此基礎(chǔ)上考慮了頻率受限情形下的切換系統(tǒng)模型降階.針對(duì)離散時(shí)間切換系統(tǒng), Birouche[18]提出了通過(guò)求解各子系統(tǒng)相關(guān)的可控/可觀格拉姆矩陣來(lái)實(shí)現(xiàn)平衡截?cái)嗄Ｐ徒惦A.通過(guò)矩陣不等式求解切換系統(tǒng)格拉姆矩陣的思想在馬爾可夫切換系統(tǒng)的模型降階問(wèn)題中也得到了相應(yīng)的推廣[19-22], 但這類方法需要通過(guò)線性矩陣不等式計(jì)算來(lái)求解所需格拉姆矩陣, 計(jì)算復(fù)雜度較高, 僅適用于求解小規(guī)模切換系統(tǒng)的模型降階問(wèn)題.Monshizadeh 等[23]針對(duì)狀態(tài)矩陣可交換的任意切換線性系統(tǒng), 將共同可控/可觀格拉姆矩陣定義為一組特殊矩陣方程的解, 進(jìn)一步給出了保持狀態(tài)矩陣可交換性的平衡截?cái)嗨惴?注意到切換系統(tǒng)與雙線性系統(tǒng)結(jié)構(gòu)上的相似之處, Duff等[24]提出了基于雙線性結(jié)構(gòu)描述下系統(tǒng)可控/可觀格拉姆矩陣的平衡截?cái)嗨惴? Strom 等[25]通過(guò)對(duì)切換系統(tǒng)無(wú)限能量格拉姆矩陣的深入研究, 給出了可提供L2 誘導(dǎo)范數(shù)意義下誤差界的平衡截?cái)嗨惴?

周期切換系統(tǒng)是一類在航空系統(tǒng)、開關(guān)電源、多速率采樣系統(tǒng)等領(lǐng)域具有重要現(xiàn)實(shí)意義的切換系統(tǒng)[26-29].對(duì)離散時(shí)間周期切換系統(tǒng)的模型降階的研究開展較早.如通過(guò)采用系統(tǒng)提升(lifting)技術(shù)將周期切換系統(tǒng)轉(zhuǎn)換為一個(gè)高維的線性時(shí)不變系統(tǒng), Varga[30]給出了相應(yīng)的平衡截?cái)嗄Ｐ徒惦A算法; Farhood 等[31]進(jìn)一步完善了該方法; Hossain 等[32]和Benner 等[33]針對(duì)廣義周期切換系統(tǒng)進(jìn)一步給出了該方法的推廣形式, 并給出了適用于大規(guī)模周期切換系統(tǒng)的Lyapunov 方程低秩快速求解數(shù)值算法; 通過(guò)引入“快照”法求解近似格拉姆矩陣的思想,Ma等[34]給出了一類可實(shí)現(xiàn)快速求解的離散時(shí)間周期切換系統(tǒng)模型降階方法.但是, 針對(duì)連續(xù)時(shí)間周期切換系統(tǒng), 目前還未見較好的模型降階方法報(bào)道.

在電力電子系統(tǒng)如Buck/Boost 變換器中, 子系統(tǒng)間的切換速率很快, 切換信號(hào)通常為高頻的周期性信號(hào), 本工作針對(duì)這類快速周期切換系統(tǒng)的模型降階問(wèn)題展開研究.一方面, 通過(guò)引入狀態(tài)平均法, 即首先求取給定周期切換系統(tǒng)的直流平均模型以及交流小信號(hào)平均模型來(lái)描述其在直流輸入和交直流輸入情形下的“平均”動(dòng)態(tài)特性[35-36]; 另一方面, 結(jié)合兩類平均模型中參數(shù)矩陣的結(jié)構(gòu)特性, 應(yīng)用奇異攝動(dòng)平衡截?cái)嗬碚摲謩e給出了相應(yīng)的降階周期切換各子系統(tǒng)模型參數(shù)的兩類求解算法.兩類算法均保持了快切換條件下的系統(tǒng)穩(wěn)定性, 同時(shí)在“平均”動(dòng)態(tài)特性意義下給出了相應(yīng)的模型逼近誤差性能先驗(yàn)分析.最后, 應(yīng)用仿真算例說(shuō)明了所提算法的有效性和優(yōu)越性.

1 問(wèn)題描述

考慮連續(xù)時(shí)間周期切換線性系統(tǒng)

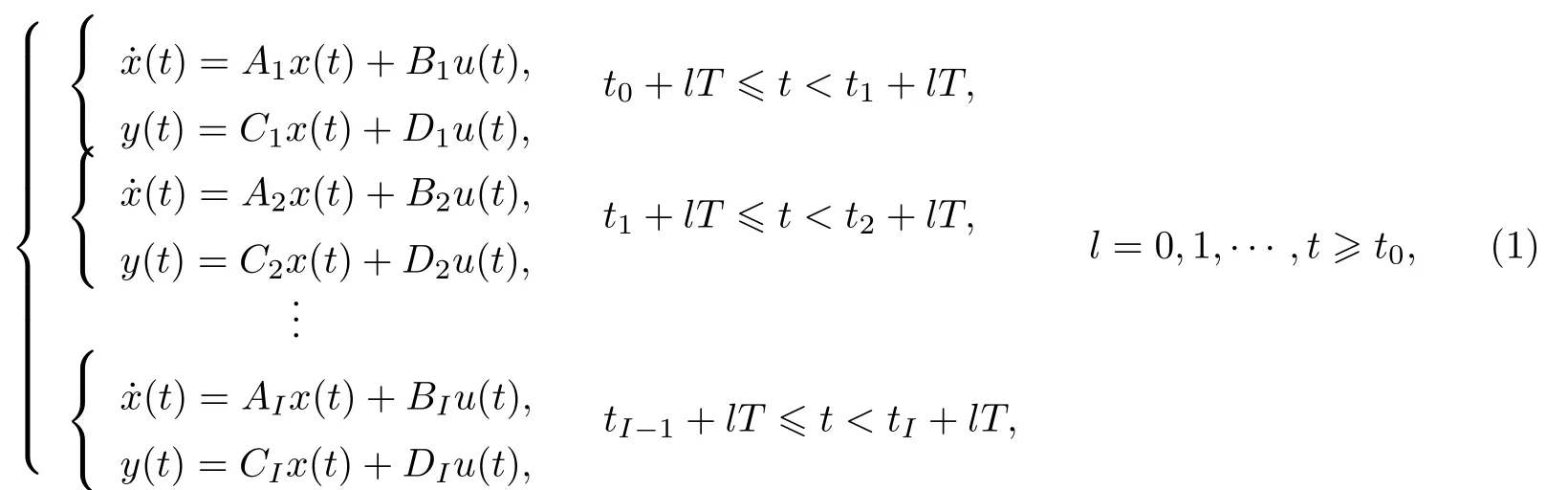
式中:x(t)∈Rn是狀態(tài)向量;y(t)∈Cp是輸出信號(hào);u(t)∈Rm是輸入信號(hào); 切換周期為T,在每個(gè)周期中第i個(gè)子系統(tǒng)(Ai,Bi,Ci,Di)的激活時(shí)長(zhǎng)為?tk=ti ?ti?1.定義一組周期切換信號(hào)pi(t),

則周期切換系統(tǒng)(1)可以表示為

式中:

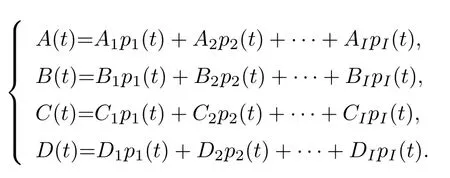
本工作主要考慮快周期切換系統(tǒng)(即切換周期T較小)的模型降階問(wèn)題, 即通過(guò)數(shù)學(xué)方法在已知給定切換系統(tǒng)模型的基礎(chǔ)上求取一個(gè)低階的快周期切換系統(tǒng)模型

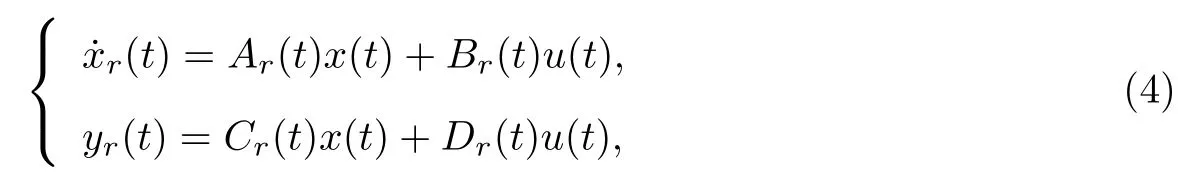
近似地描述給定周期切換系統(tǒng)(1)的輸入輸出動(dòng)態(tài)特性, 同時(shí)保持原系統(tǒng)的穩(wěn)定性等基本性質(zhì).(Ar(t),Br(t),Cr(t),Dr(t))由待求的低階子系統(tǒng)模型參數(shù)(Ari,Bri,Cri,Dri,i= 1,2,··· ,I)和與原系統(tǒng)相同的周期切換信號(hào)pi(t)組成, 即

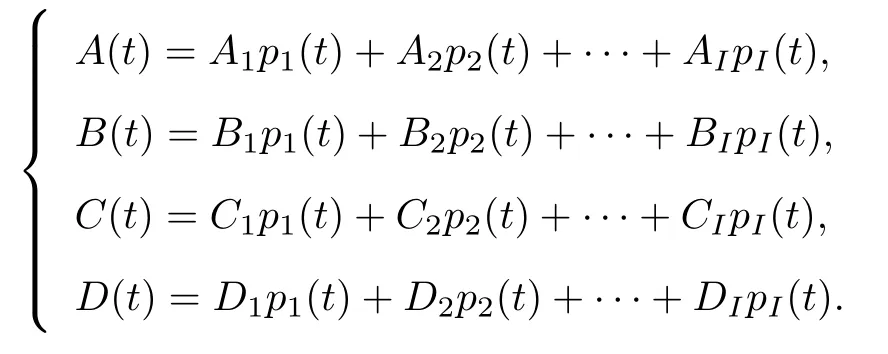
2 周期快切換系統(tǒng)平衡截?cái)嗄Ｐ偷慕惦A

2.1 基于穩(wěn)態(tài)線性平均模型

狀態(tài)空間平均法是平均法的一階近似, 是電力電子系統(tǒng)(如各種類型的DC-DC 轉(zhuǎn)換器)進(jìn)行瞬態(tài)建模分析的常用方法.定義第i個(gè)子系統(tǒng)的占空比為

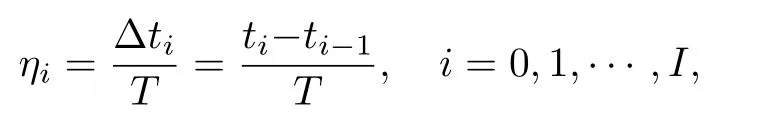
系統(tǒng)的平均狀態(tài)為

式中:x(t)為周期切換系統(tǒng)的真實(shí)狀態(tài).通過(guò)一階近似法, 容易得到周期切換系統(tǒng)的直流平均模型

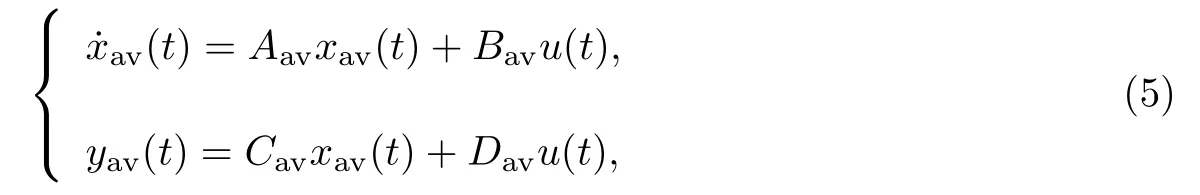
式中:

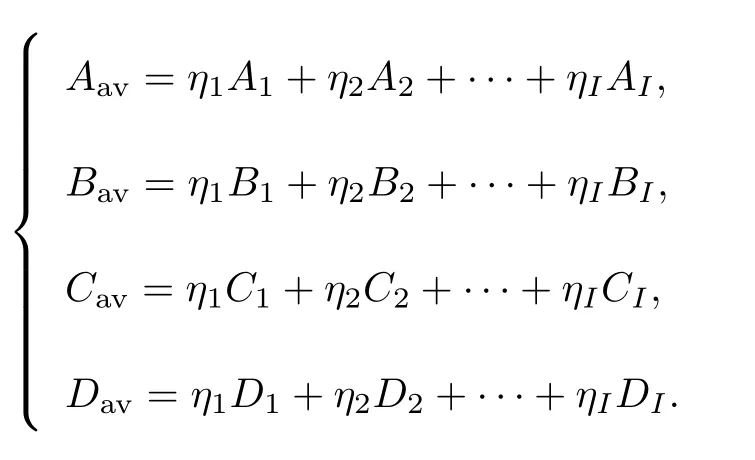
借助狀態(tài)空間平均模型(5), 可以采用線性時(shí)不變系統(tǒng)的方法和工具分析周期切換系統(tǒng)的穩(wěn)態(tài)特性, 同時(shí)還可以得到周期切換系統(tǒng)的一個(gè)弱穩(wěn)定性分析條件.

引理1[26-27]考慮周期切換系統(tǒng)(1), 如果其狀態(tài)空間平均模型穩(wěn)定, 即Aav為Hurwitz 矩陣, 則一定存在足夠快的切換頻率f=1/T使得周期切換系統(tǒng)(1)穩(wěn)定.

基于線性時(shí)不變的狀態(tài)空間平均模型(5), 給出借助奇異攝動(dòng)型平衡截?cái)嗟乃惴▉?lái)求解降級(jí)的各周期切換子系統(tǒng)模型參數(shù)矩陣.

算法1基于直流平均模型的切換系統(tǒng)平衡截?cái)嗄Ｐ徒惦A.

輸入: 給定線性切換系統(tǒng)模型(Ai,Bi,Ci,Di)以及降階模型數(shù)r.

(1) 求解關(guān)于平均狀態(tài)空間模型的可控/可觀Lyapunov 方程:

(2) 對(duì)矩陣進(jìn)行Cholesky 分解:=Uav.

(3) 對(duì)矩陣av進(jìn)行特征值分解:=Vav, 其中Σav= diag{σav1,σav2,··· ,σavn}.

(4) 計(jì)算相應(yīng)的坐標(biāo)變換矩陣:Tav=.

(5) 通過(guò)坐標(biāo)變換計(jì)算給定穩(wěn)態(tài)平均模型的平衡實(shí)現(xiàn)以及各切換子系統(tǒng)模型的平衡實(shí)現(xiàn):

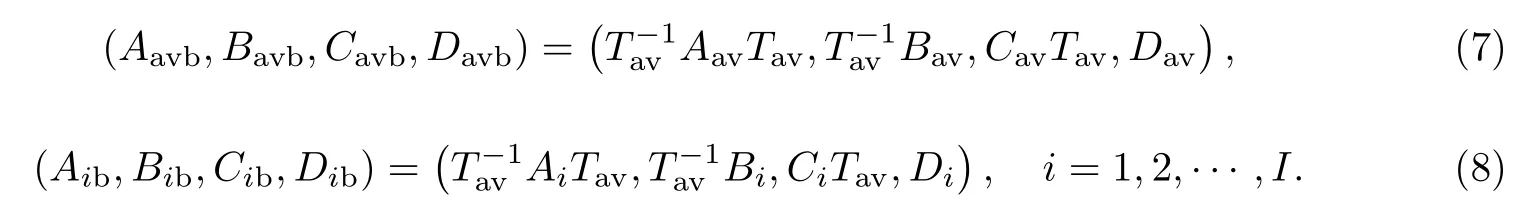
(6) 根據(jù)待求解降階模型階數(shù)r對(duì)各平衡實(shí)現(xiàn)下的狀態(tài)空間參數(shù)矩陣進(jìn)行分塊, 可得

式中:Aavb11,Aib11∈Rr×r;Bavb1,Cib1∈Rr×p;Cavb1,Cib1∈Rm×r.進(jìn)而, 根據(jù)

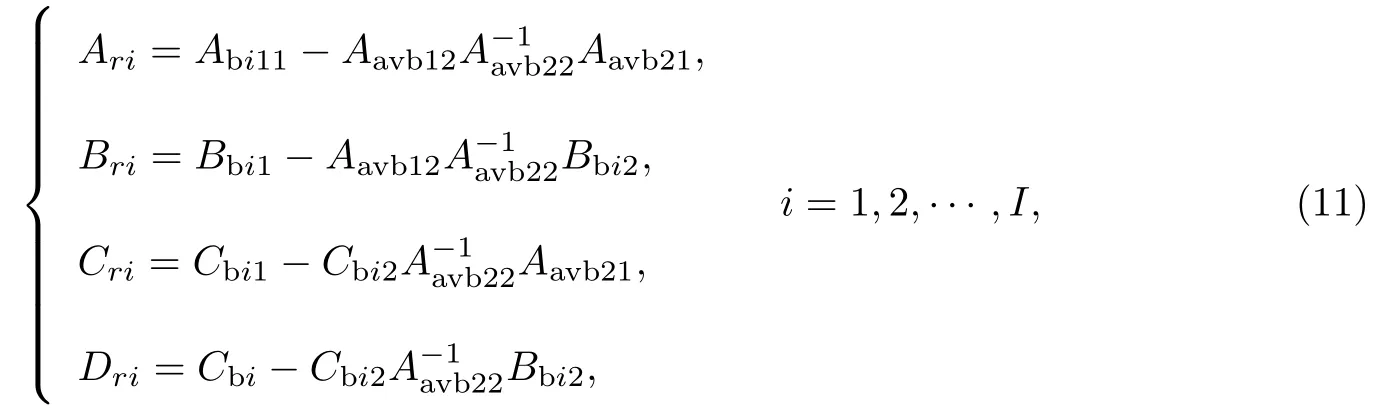
生成待求的降階快周期切換系統(tǒng)各子系統(tǒng)模型參數(shù)矩陣.

輸出: 低階線性切換系統(tǒng)模型(Ari,Bri,Cri,Dri).

定理1算法1 生成的降階周期切換系統(tǒng)同樣滿足弱穩(wěn)定性(即存在足夠高的切換頻率使得其穩(wěn)定), 降階周期切換系統(tǒng)的直流平均模型與原周期切換系統(tǒng)的直流平均模型(5)在直流輸入下的誤差為0, 即

同時(shí), 在全頻域上的逼近性能存在H∞范數(shù)意義下的誤差界:

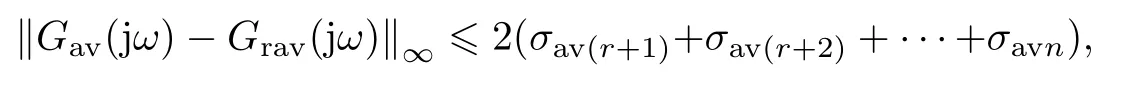
其 中Grav(jω) =Crav(jωI ?Arav)?1Brav+Drav為 降 階 周 期 切 換 系 統(tǒng) 直 流 平 均 模 型(Arav,Brav,Crav,Drav)的傳遞函數(shù).

證明 設(shè)()為直流平均模型(5)采用奇異攝動(dòng)平衡截?cái)嗨傻慕惦A模型.結(jié)合式(5)中關(guān)于周期切換系統(tǒng)直流平均模型的定義以及算法1 中降階周期切換系統(tǒng)各子系統(tǒng)模型參數(shù)的計(jì)算公式, 可推得

不難看出, 降階周期切換系統(tǒng)的直流平均模型Grav(jω)(Arav,Brav,Crav,Drav)與直接對(duì)原系統(tǒng)直流平均模型進(jìn)行奇異攝動(dòng)平衡截?cái)嗄Ｐ徒惦A所得線性時(shí)不變模型(jω)()完全一致, 根據(jù)奇異攝動(dòng)平衡截?cái)嗬碚揫1-3]可知,為Hurwitz 矩陣且滿足

其中(jω) =(j)?1+為相應(yīng)線性時(shí)不變降階系統(tǒng)的傳遞函數(shù).進(jìn)一步根據(jù)引理1 可知, 降階周期切換系統(tǒng)具有快切換條件下的弱穩(wěn)定性, 同時(shí)定理1 中描述的頻域逼近性能成立, 即有

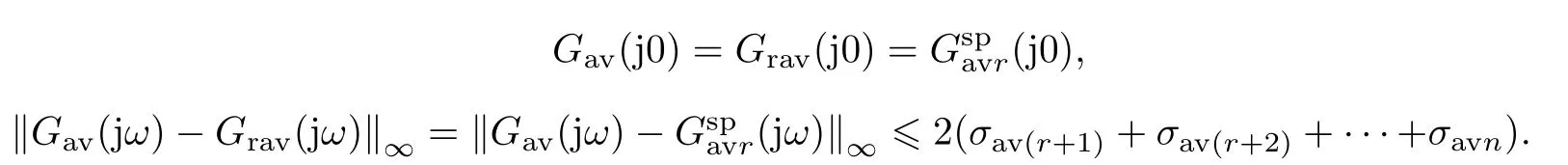
注1針對(duì)線性時(shí)不變系統(tǒng)的模型降階問(wèn)題, 平衡截?cái)喾ㄓ袠?biāo)準(zhǔn)型和奇異攝動(dòng)型2 種生成相同全頻域誤差上界的降階系統(tǒng)參數(shù)矩陣求解形式, 采用標(biāo)準(zhǔn)型平衡截?cái)喾傻玫捷^好的高頻段模型逼近性能(其中降階模型與原模型在ω=∞處完全匹配), 而采用奇異攝動(dòng)型平衡截?cái)喾▌t可得到較好的低頻段模型性能(其中降階模型與原模型在ω=0 處完全匹配), 關(guān)于這2種類型的平衡截?cái)嘣敿?xì)介紹見文獻(xiàn)[1,3].當(dāng)系統(tǒng)輸入為直流信號(hào)即零頻信號(hào)時(shí), 在算法1 中對(duì)直流平均模型采用奇異攝動(dòng)型平衡截?cái)囡@然更為合理.

2.2 基于交流小信號(hào)平均模型

對(duì)于許多實(shí)際周期切換系統(tǒng), 其輸入往往存在直流信號(hào)之外的交流攝動(dòng)信號(hào), 且交流攝動(dòng)信號(hào)的幅度遠(yuǎn)小于直流信號(hào).此外, 系統(tǒng)的切換時(shí)間也有可能存在攝動(dòng).在這種情況下通常采用小信號(hào)方法來(lái)建立周期切換系統(tǒng)的交流小信號(hào)平均模型, 進(jìn)行系統(tǒng)動(dòng)態(tài)分析[35].如果系統(tǒng)的切換頻率遠(yuǎn)大于系統(tǒng)的自然頻率以及交流攝動(dòng)信號(hào)的頻率, 則交流小信號(hào)平均模型可以很好地描述系統(tǒng)在交流攝動(dòng)情形下的動(dòng)態(tài)響應(yīng)特性[36].

首先, 假設(shè)周期切換系統(tǒng)在直流輸入u(t) =U會(huì)達(dá)到一個(gè)平衡態(tài)X, 該平衡態(tài)由下列方程建立:

當(dāng)輸入信號(hào)中疊加有小的交流攝動(dòng)攝動(dòng)信號(hào)時(shí)(即u(t) =U+uac(t), 其中uac(t)表示小的交流攝動(dòng)信號(hào)), 令ηi(t)=ηi+ηpi(t)表示第i個(gè)子系統(tǒng)在一個(gè)周期內(nèi)的激活時(shí)間函數(shù), 其中ηpi(t)上的攝動(dòng)相應(yīng)的系統(tǒng)的狀態(tài)x(t)、輸出y(t)以及占空比均可表示為下列穩(wěn)態(tài)加攝動(dòng)的形式:

將式(13)帶入系統(tǒng)的動(dòng)態(tài)方程(1), 可得

進(jìn)一步整理式(14), 可得

根據(jù)式(12), 可以消掉式(15)中的直流項(xiàng).此外, 基于交流攝動(dòng)為小信號(hào)的假設(shè), 忽略式(15)中微小的二次非線性項(xiàng)不會(huì)帶來(lái)嚴(yán)重的系統(tǒng)分析誤差, 因此可得到如下線性的交流小信號(hào)平均模型:

式(16)可進(jìn)一步整理為

式中: 系統(tǒng)矩陣(Aav,Bav,Cav,Dav)及輸入信號(hào)ˉup(t)分別為

其中

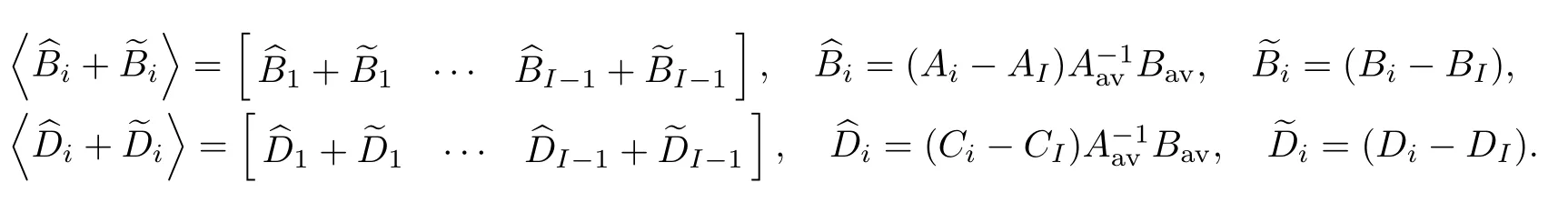
基于上述周期切換系統(tǒng)的交流小信號(hào)平均模型, 下面給出結(jié)合標(biāo)準(zhǔn)平衡截?cái)喾ǖ闹芷谇袚Q系統(tǒng)模型降階算法

算法2基于小信號(hào)交流平均模型的切換系統(tǒng)平衡截?cái)嗄Ｐ徒惦A算法.

輸入: 給定線性切換系統(tǒng)模型(Ai,Bi,Ci,Di)以及降階模型數(shù)r.

(1) 求解關(guān)于平均狀態(tài)空間模型的可控/可觀Lyapunov 方程:

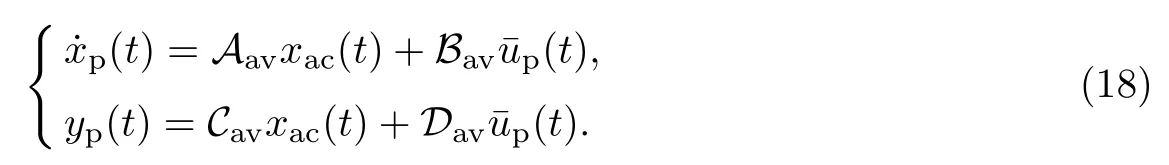
(2) 對(duì)矩陣進(jìn)行Cholesky 分解:=.

(3) 對(duì)矩陣進(jìn)行特征值分解:=, 其中Σav=diag{σav1,σav2,··· ,σavn}.

(4) 計(jì)算相應(yīng)的坐標(biāo)變換矩陣:Tav=.

(5) 通過(guò)坐標(biāo)變換計(jì)算給定切換系統(tǒng)小信號(hào)交流平均模型以及各子系統(tǒng)模型的平衡實(shí)現(xiàn):

(6) 根據(jù)待求解降階模型階數(shù)r對(duì)各平衡實(shí)現(xiàn)下的狀態(tài)空間參數(shù)矩陣進(jìn)行分塊, 可得

式中:Aavb11∈Rr×r;Bavb1,,∈Rr×p;Cavb1,,∈Rm×r.進(jìn)一步可根據(jù)下式

生成待求的降階快周期切換系統(tǒng)模型參數(shù)矩陣, 其中0< α <1為可調(diào)參數(shù), 通常選取為交流攝動(dòng)信號(hào)與直流信號(hào)之比的估計(jì)值, ()為交流小信號(hào)平均模型(17)采用奇異攝動(dòng)平衡截?cái)嗨傻慕惦A模型參數(shù)矩陣:

輸出: 低階線性切換系統(tǒng)模型(Ari,Bri,Cri,Dri).

定理2算法2 生成的降階周期切換系統(tǒng)同樣滿足弱穩(wěn)定性(即存在足夠高的切換頻率使得其穩(wěn)定), 降階周期切換系統(tǒng)的交流小信號(hào)平均模型與原周期切換系統(tǒng)的交流小信號(hào)平均模型(17)在全頻域上的逼近性能存在下列H∞范數(shù)意義下的誤差界:

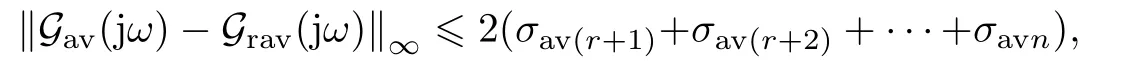
其中Grav(jω) =Crav(jωI ?Arav)?1Brav+Drav為降階周期切換系統(tǒng)交流小信號(hào)平均模型(Arav,Brav,Crav,Drav) 的傳遞函數(shù).

證明 結(jié)合式(17)中關(guān)于交流小信號(hào)平均模型的定義以及算法2 中各降階子系統(tǒng)模型參數(shù)的計(jì)算公式可得

進(jìn)一步, 可以證明

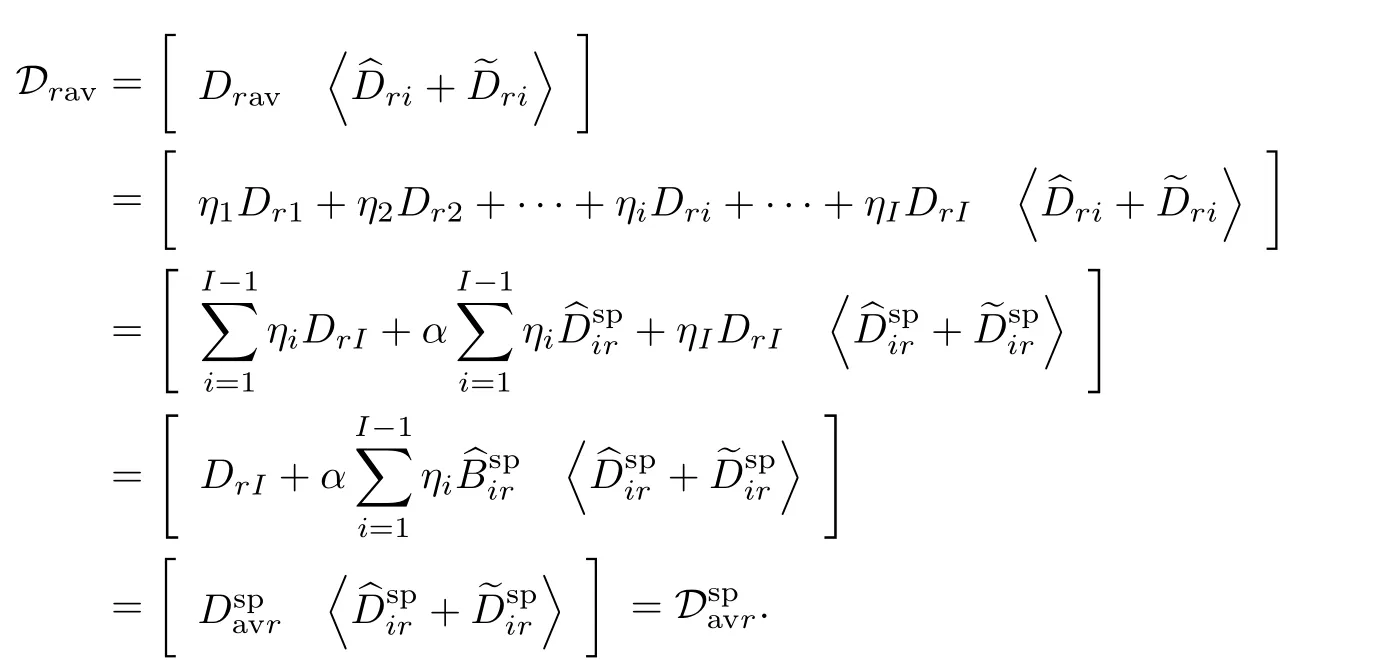
同樣不難看出, 降階周期切換系統(tǒng)的交流小信號(hào)平均模型Grav(jω)(Arav,Brav,Crav,Drav)與直接對(duì)原系統(tǒng)交流小信號(hào)平均模型(17)進(jìn)行標(biāo)準(zhǔn)平衡截?cái)嗄Ｐ徒惦A所得線性時(shí)不變模型(jω)()完全一致, 根據(jù)標(biāo)準(zhǔn)平衡截?cái)嗬碚摽芍獮镠urwitz 矩陣滿足

進(jìn)一步根據(jù)引理1 可知, 降階周期切換系統(tǒng)具有快切換條件下的弱穩(wěn)定性, 同時(shí)其交流小信號(hào)模型滿足全頻域下的逼近誤差性能:

注2與算法1 相同, 算法2 中同樣采用奇異攝動(dòng)型平衡截?cái)鄟?lái)對(duì)首先生成平均模型的降階系統(tǒng)參數(shù); 但由于直流平均模型與交流小信號(hào)模型結(jié)構(gòu)的不同, 算法2 中采用了與算法1 不同的方式來(lái)生成降階周期切換子系統(tǒng)的模型參數(shù), 但生成兩類算法的初衷都在于使其降階周期切換系統(tǒng)的平均模型與平均模型的降階系統(tǒng)相匹配.

注3 周期切換系統(tǒng)作為一類特殊的切換系統(tǒng), 采用針對(duì)一般切換系統(tǒng)開發(fā)的模型降階方法[14,23-24]在理論上是可行的, 但這些方法均需假設(shè)各子系統(tǒng)必須為漸進(jìn)穩(wěn)定, 且求解算法涉及多組Lyapunov 或廣義Lyapunov 方程, 甚至Lyapunov 矩陣不等式的求解.本工作中的兩類算法中均不需要假設(shè)切換系統(tǒng)的子系統(tǒng)漸進(jìn)穩(wěn)定, 只要其平均模型穩(wěn)定即可進(jìn)行求解, 同時(shí)算法中僅涉及到一組Lyapunov 方程求解以及一些簡(jiǎn)單的矩陣運(yùn)算, 可以更為方便地處理周期切換系統(tǒng)的模型降階問(wèn)題.

3 仿真算例

考慮Henry[37]給出的一個(gè)關(guān)于梯形拓?fù)浣Y(jié)構(gòu)下四級(jí)交換電容式直流對(duì)直流(DC-DC)轉(zhuǎn)換器的建模案例, 其電路結(jié)構(gòu)如圖1 所示.

圖1 梯形拓?fù)浣Y(jié)構(gòu)四級(jí)交換電容式轉(zhuǎn)換器電路結(jié)構(gòu)示意圖Fig.1 Schematic diagram of four-stage SC converter with a ladder topology

圖1 所示的10 個(gè)“開關(guān)/切換”元件為FDMS8460 MOSFETs, 其等效開關(guān)電阻用Rsw=0.003 表示, 8 個(gè)電容元件均為Nichicon 的陶瓷電容, 其電容值Cc= 25, 等效電阻為Rc=0.001.以各電容的兩端電壓作為狀態(tài),Vin,Vout2 個(gè)端口的電壓信號(hào)作為系統(tǒng)的輸入, 電容C1的兩端電壓信號(hào)作為系統(tǒng)的輸出, 根據(jù)其開關(guān)元件的狀態(tài)[37], 該切換電路的切換周期為0.50 s, 2 個(gè)切換模式即子系統(tǒng)的占空比均為0.5, 即各自在一個(gè)周期內(nèi)的激活時(shí)間均為0.25 s.借助基爾霍夫電壓電流定理對(duì)該電路進(jìn)行分析建模, 可求得該電路在切換模式1 和2 下的狀態(tài)空間方程為

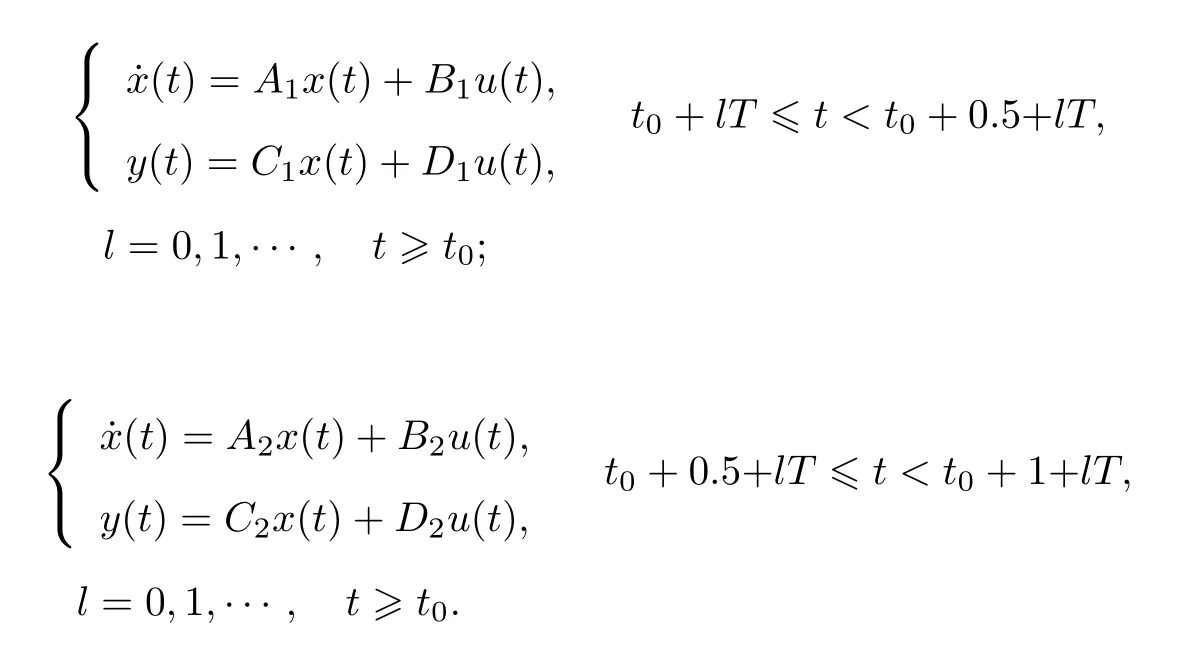
2 個(gè)切換模式下的子系統(tǒng)參數(shù)矩陣分別為

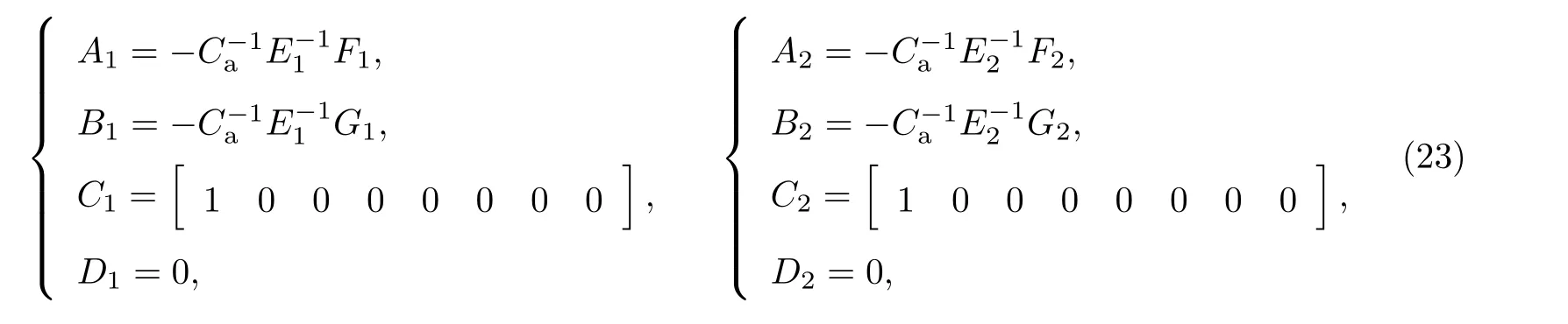
式中:Ca為由各電容的電容值組成的對(duì)角矩陣,Ca=diag{Cc,Cc,··· ,Cc};E1,F1,G1和E2,F2,G2包含了電路在2 個(gè)不同切換模式下的開關(guān)元件的狀態(tài)信息以及其他參數(shù)信息, 分別為

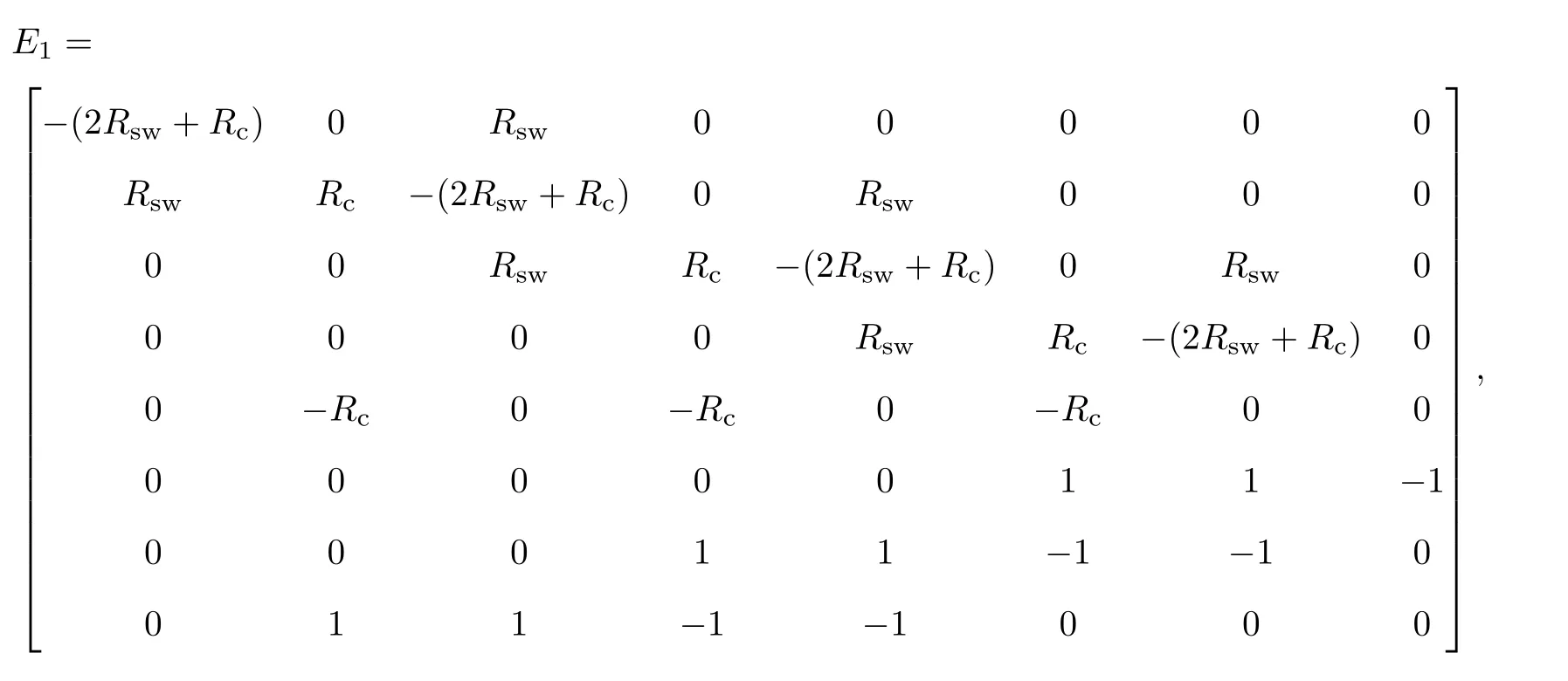
通過(guò)Matlab 計(jì)算不難發(fā)現(xiàn), 上述電路的2 個(gè)切換子系統(tǒng)均存在虛軸上的極點(diǎn), 無(wú)法直接應(yīng)用Petreczky 等[14]提出的線性矩陣不等式方法來(lái)求解其共同格拉姆矩陣, 也無(wú)法直接應(yīng)用Monshizadeh 等[23]給出的子系統(tǒng)格拉姆矩陣平均法進(jìn)行求解.幸運(yùn)的是, 該電路的直流平均模型/交流小信號(hào)平均模型中的平均狀態(tài)矩陣Aav=Aav=0.5A1+0.5A2為Hurwitz 矩陣, 可直接應(yīng)用本方法中的算法1 或算法2 進(jìn)行求解.

(1) 首先考慮輸入為直流信號(hào)的情況.設(shè)需要的降階模型階數(shù)為2, 則基于直流平均模型(5)通過(guò)算法1 生成2 階的周期切換子系統(tǒng)模型參數(shù)矩陣:

為直觀地展現(xiàn)降階后的2 階周期切換模型對(duì)原8 階周期切換系統(tǒng)的逼近性能, 可以通過(guò)Matlab 進(jìn)行仿真驗(yàn)證, 在仿真程序中輸入如下直流信號(hào):

圖2 為仿真所得2 階周期切換系統(tǒng)在直流輸入下的輸出信號(hào).

圖2 算法1 所得2 階周期切換系統(tǒng)在直流輸入下的逼近性能Fig.2 Approximation performance of the 2nd reduced switched systems obtained by using Algorithm 1 in the presence of DC input

從圖2 可以看出, 在相同的(零頻)直流輸入信號(hào)激勵(lì)下, 算法1 所得2 階降階周期切換模型對(duì)原8 階周期切換系統(tǒng)具有良好的逼近效果, 相應(yīng)的輸出誤差非常小, 充分說(shuō)明了算法1 在直流輸入情形下的有效性.同時(shí), 2 個(gè)周期切換系統(tǒng)的直流平均模型所得輸出誤差收斂為0, 這與定理1 給出的理論分析結(jié)果相符.

(2) 考慮輸入在直流信號(hào)之外存在交流攝動(dòng)信號(hào)以及切換時(shí)間存在攝動(dòng)的情況.同樣假設(shè)所需降階模型的階數(shù)為2, 則基于交流小信號(hào)平均模型(17), 可應(yīng)用算法2 得到相應(yīng)的2 階周期切換子系統(tǒng)模型參數(shù)矩陣:

令算法2 中的可調(diào)參數(shù)α=0.1, 即設(shè)交流攝動(dòng)信號(hào)與直流信號(hào)之比的估計(jì)值約為0.1.該2 階周期切換模型在存在交流攝動(dòng)以及切換時(shí)間攝動(dòng)情形下的逼近性能同樣可通過(guò)Matlab 進(jìn)行仿真驗(yàn)證.在直流信號(hào)的基礎(chǔ)上增加交流攝動(dòng)信號(hào), 式(24)變換為

令切換時(shí)間的攝動(dòng)值為

圖3 為標(biāo)準(zhǔn)周期切換信號(hào)和帶有切換時(shí)間攝動(dòng)的周期切換信號(hào).由圖3 可知, 子系統(tǒng)1 在T=0.5 s 的切換周期中的激活時(shí)間由0.250 0 s 攝動(dòng)為0.292 4 和0.207 6 s.

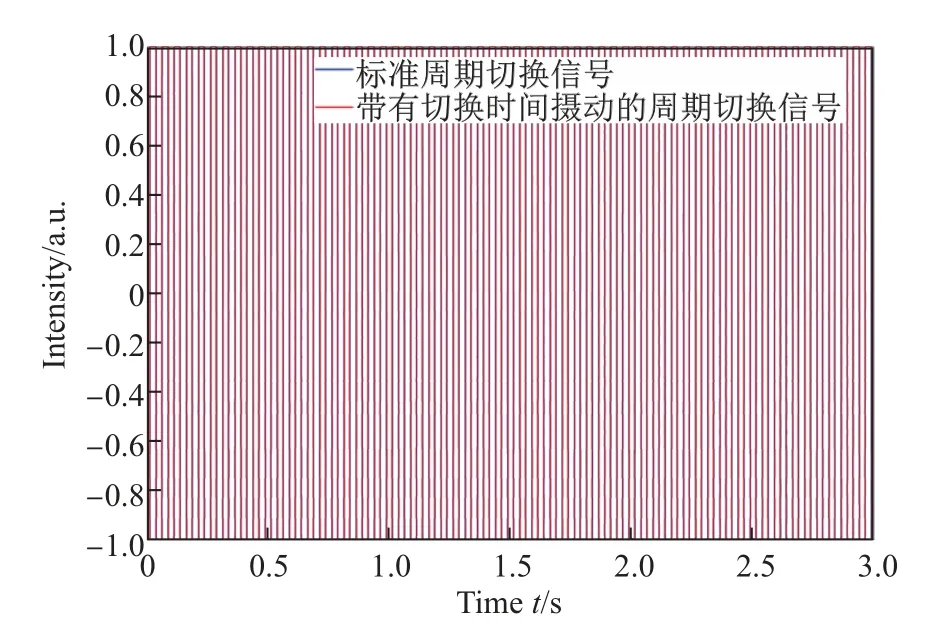
圖3 標(biāo)準(zhǔn)周期切換信號(hào)與帶有切換時(shí)間攝動(dòng)的周期切換信號(hào)Fig.3 Periodically switching signal and perturbed periodically switching signal

為與算法1 中所得降階模型進(jìn)行比較, 圖4 分別給出了通過(guò)算法2 以及算法1 分別得到的降階周期切換模型與原模型之間逼近性能的曲線, 包括原8 階周期切換系統(tǒng)與2 階周期切換模型的輸出曲線以及相應(yīng)的輸出誤差曲線.

通過(guò)圖4 可以看出, 相對(duì)于基于直流平均模型的降階算法1, 采用基于交流小信號(hào)平均模型的算法2 所得到的2 階降階模型在帶有交流攝動(dòng)輸入信號(hào)以及切換時(shí)間攝動(dòng)的情形下有著更好的逼近性能.這進(jìn)一步說(shuō)明了在考慮交流攝動(dòng)輸入信號(hào)以及切換時(shí)間攝動(dòng)的情況下設(shè)計(jì)算法2 的必要性.

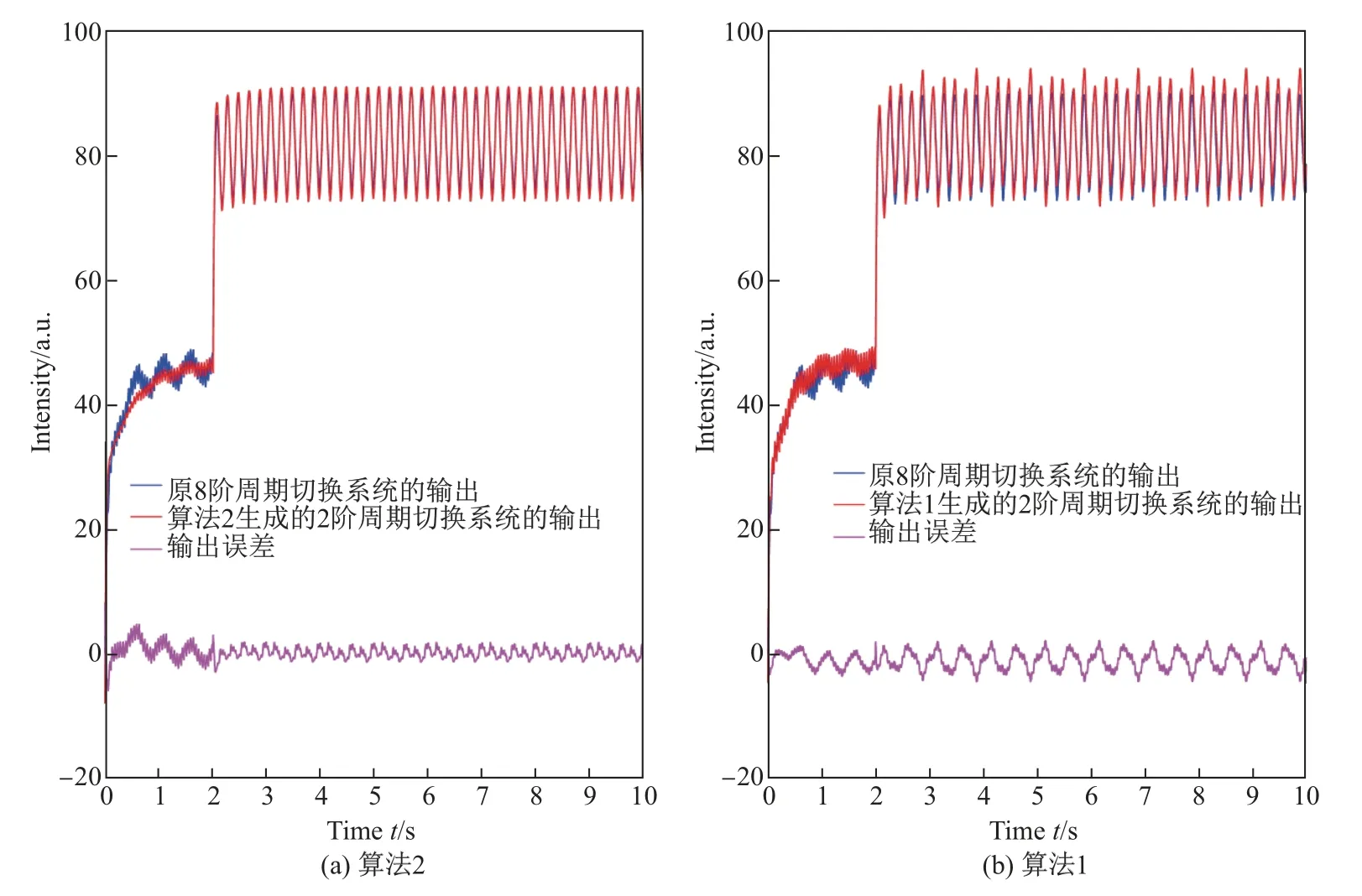
圖4 2 階周期切換系統(tǒng)在直流-交流輸入以及切換時(shí)間攝動(dòng)情形下的逼近性能Fig.4 Approximation performance of the 2nd reduced switched systems obtained by using Algorithm 2 and Algorithm 1 in the presence of DC-AC input as well as switched time perturbation

通過(guò)仿真算例可以得出, 算法1 非常適用于僅存在直流輸入情形下的快周期切換系統(tǒng)模型降階問(wèn)題, 而對(duì)存在交流攝動(dòng)輸入信號(hào)以及切換時(shí)間攝動(dòng)的快周期切換系統(tǒng)模型降階問(wèn)題,則可以考慮采用算法2 來(lái)求解相應(yīng)的降階周期切換系統(tǒng)模型參數(shù)矩陣.

4 結(jié)束語(yǔ)

針對(duì)快周期切換系統(tǒng)的模型降階問(wèn)題, 本工作通過(guò)引入其直流平均模型和交流小信號(hào)平均模型, 結(jié)合奇異攝動(dòng)平衡截?cái)嗬碚摲謩e給出了兩類求解降階周期切換模型參數(shù)矩陣的算法.這兩類算法均可保持原系統(tǒng)在快周期切換下的穩(wěn)定性, 同時(shí)可分別生成逼近系統(tǒng)在僅有直流輸入以及存在交流攝動(dòng)與切換時(shí)間攝動(dòng)輸入情形下輸入輸出相應(yīng)特性的降階模型.應(yīng)用仿真例子驗(yàn)證了所提算法的有效性以及兩類算法的不同適用范圍.