基于GRU循環神經網絡輔助的組合導航算法

陶毅峰，江金光，方 偉

(武漢大學 衛星導航定位技術研究中心，湖北 武漢 430079)

0 引 言

基于捷聯慣性導航系統和GPS(global positioning system)技術，在GPS信號良好的情況下可以有效地進行導航[1]。卡爾曼濾波(Kalman filtering)技術由于其高精度，設計簡單等優點成為了最廣泛使用的技術。因為高精度慣性測量單元(inertial measurement unit，IMU)成本昂貴，大部分情況下IMU只是MEMS(microelectro mechanical systems)級別的，這種級別的INS(inertial navigation system)/GPS組合導航系統的定位精度極大地依賴于GPS信號[2]，而GPS信號極易受到高樓、樹蔭等遮擋而失鎖[3-5]；此時INS/GPS組合導航系統僅能依靠純慣導進行機械編排，定位結果會隨著時間的積累發散[6]，導致解算精度迅速下降。而神經網絡作為近幾年火熱的技術，已有許多結合神經網絡與INS/GPS的研究[7,8]。如利用BP(back propagation)神經網絡[9]、多層感知器(multi-layer perceptron，MLP)[10]來輔助組合導航系統。這些模型將各時刻的輸入與輸出視為獨立的元素，但是實際的組合導航系統顯然是一個連續的、各時刻位置相關的系統。循環神經網絡(recurrent neural network，RNN)可以將過去時刻的位置信息與當前時刻的輸出聯系起來，恰好與上述問題契合。因此本文使用循環神經網絡中的一種變體結構GRU(gated recurrent unit)算法輔助組合導航系統，以解決GPS失鎖時定位精度迅速發散的問題。

1 組合導航卡爾曼濾波模型

INS/GPS組合導航系統的組合方式有：松組合、緊組合、深組合等。其中松組合是基于GPS導航結果的數據組合，即Kalman的觀測向量為GPS和INS的速度、位置的數據組合。松組合結構簡單，計算負擔低，易實現，可靠性很高，但所需衛星數最少為4顆，粗差探測能力弱。緊組合是基于GPS觀測量的數據組合，即Kalman的觀測向量為GPS的偽距、偽距率的數據組合。緊組合結構復雜，計算負擔較高，可靠性也不如松組合，但是其粗差探測能力強，可觀測衛星數少于4顆時也可以正常工作。深組合是基于GPS信號的組合，采用了矢量環路的方法，通道間互相輔助，提高了信號跟蹤環路性能和系統，降低了載體動態變化的影響[11]，但該技術還不成熟，實現難度高。

由于本文側重點為解決GPS失鎖時的精度問題，故本文選取了結構較為簡單，計算量小的松組合作為組合方式。INS/GPS松組合的結構如圖1所示，其中INS輸出慣導推算得到的信息PINS(位置)、VINS(速度)、AINS(姿態角)；GPS提供位置信息，與INS的位置信息相減作為觀測向量ZK[12]輸入到卡爾曼濾波模塊；卡爾曼濾波模塊輸出改正信息δp，δv，δA對INS的輸出值進行修正，得到最終的組合結果。

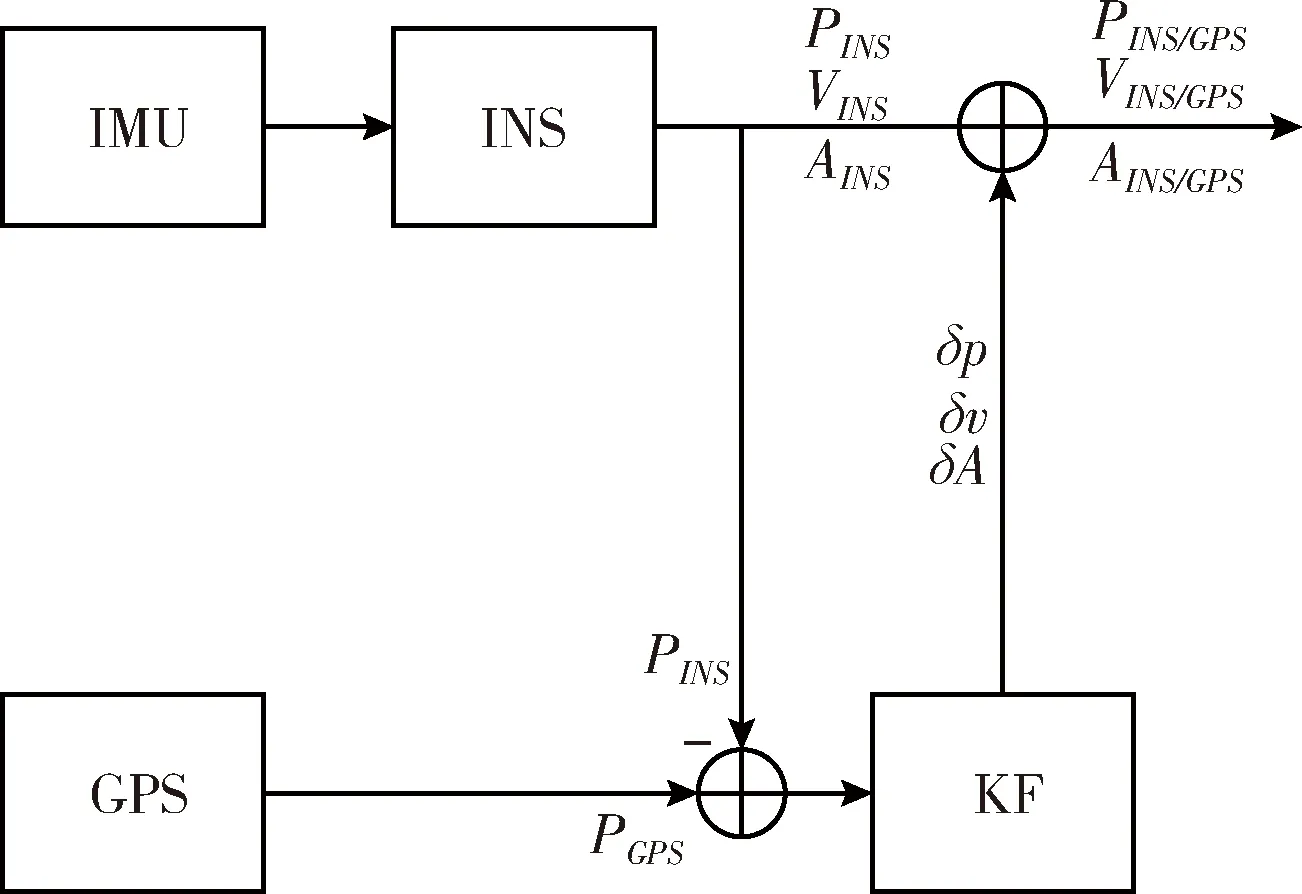
圖1 INS/GPS松組合結構框架

本文松組合采用15維卡爾曼濾波，坐標系采用北東地地理坐標系，狀態變量為

(1)

觀測向量為

Z=[PINS-GPS]

(2)

觀測值的量測矩陣為

(3)

狀態轉移矩陣為

(4)

卡爾曼濾波預測部分

(5)

更新部分

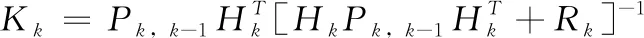
(6)

其中，φk,k-1為離散化后的狀態轉移矩陣，Qk-1為離散化后的系統狀態噪聲方差陣，Pk,k-1為一步預測狀態協方差矩陣，Kk為卡爾曼濾波增益，Pk為估計狀態協方差矩陣[13]。GPS信號正常時，每一秒內的純慣導推算帶來的誤差會被卡爾曼濾波后的δp，δv，δA所補償掉。但是一旦GPS失鎖，卡爾曼濾波就失去了觀測向量，無法繼續進行組合，也就無法產生δp，δv，δA對INS結果進行反饋。這部分的誤差一直累計，會隨時間產生二次發散。因此GPS失鎖時松組合退化為純慣導推算無法滿足正常的導航需求，需要其它觀測或算法輔助，本文的輔助導航方法在第3章中繼續詳細闡述。

2 GRU循環神經網絡模型

2.1 循環神經網絡結構

傳統的神經網絡為前饋神經網絡(feed-forward neural network，FNN)，通常包含輸入層、隱藏層和輸出層。各層之間互相連接，訓練時每一層的權值更新就是通過這些連接進行傳遞；但是每一層內的神經元互相獨立，不存在環路，因此FNN僅適用于觀測數據互相獨立的情況，而對于上下文有聯系的時間序列數據就效果欠佳。

為了彌補這一不足，RNN在隱藏層加入了回路連接，前一時刻的網絡狀態會傳遞到下一時刻，因此當前時刻的輸出不僅受到當前時刻的輸入影響，還與之前時刻的數據輸入產生了聯系。而對于權值參數的問題，RNN借鑒了隱馬爾可夫模型(hidden Markov model，HMM)參數共享的概念。HMM廣泛應用于語音處理、文字處理等領域，對于序列數據建模取得很好的效果。這二者利用內部狀態來衡量數據間的依賴關系，參數共享減少了訓練的參數，提高了效率。RNN的參數更新和傳統的神經網絡類似，使用了反向傳播算法(backpropagation algorithm)，其前向傳播如圖2所示，由于每個時刻的隱藏狀態都與前一時刻的產生聯系，因此進一步產生了長距離的依賴。

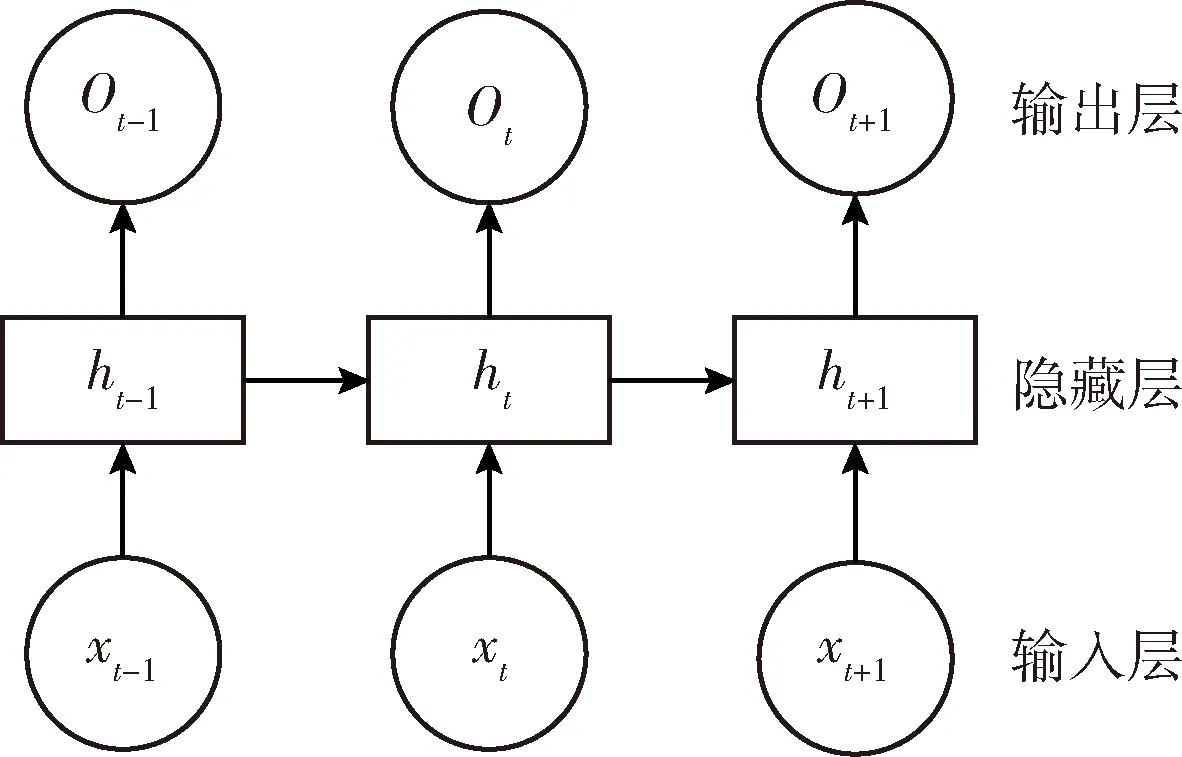
圖2 RNN前向傳播結構

2.2 GRU算法

RNN適用于處理時間序列數據，可以將當前時刻的輸出和狀態當作輸入傳遞到下一時刻，因此這種串型結構可以保持各時刻間的數據關系。但是RNN很難保持長期的依賴性，且存在梯度消失、梯度爆炸的問題[14]，因此在RNN基礎上進一步產生了許多優秀的演化模型，如長短期記憶網絡(long short-term memory，LSTM)和GRU。這些模型通過加入記憶單元來解決長期依賴的問題，通過門控單元來避免梯度爆炸。而GRU相較于LSTM參數更少，訓練更快，因此人工智能(artificial intelligence，AI)模塊選擇GRU算法。

GRU單元結構如圖3所示，ht-1是前一時刻的隱藏狀態，ht為當前時刻的隱藏狀態輸出，xt是當前時刻的數據輸入。該單元結構有2個門，更新門和重置門，更新門用于控制前一時刻的狀態信息對當前時刻的影響程度，輸出為rt，更新門的值越大，狀態信息保留越多；重置門用于忽略前一時刻的部分狀態信息，輸出為zt，重置門的值越小，狀態信息忽略越多。

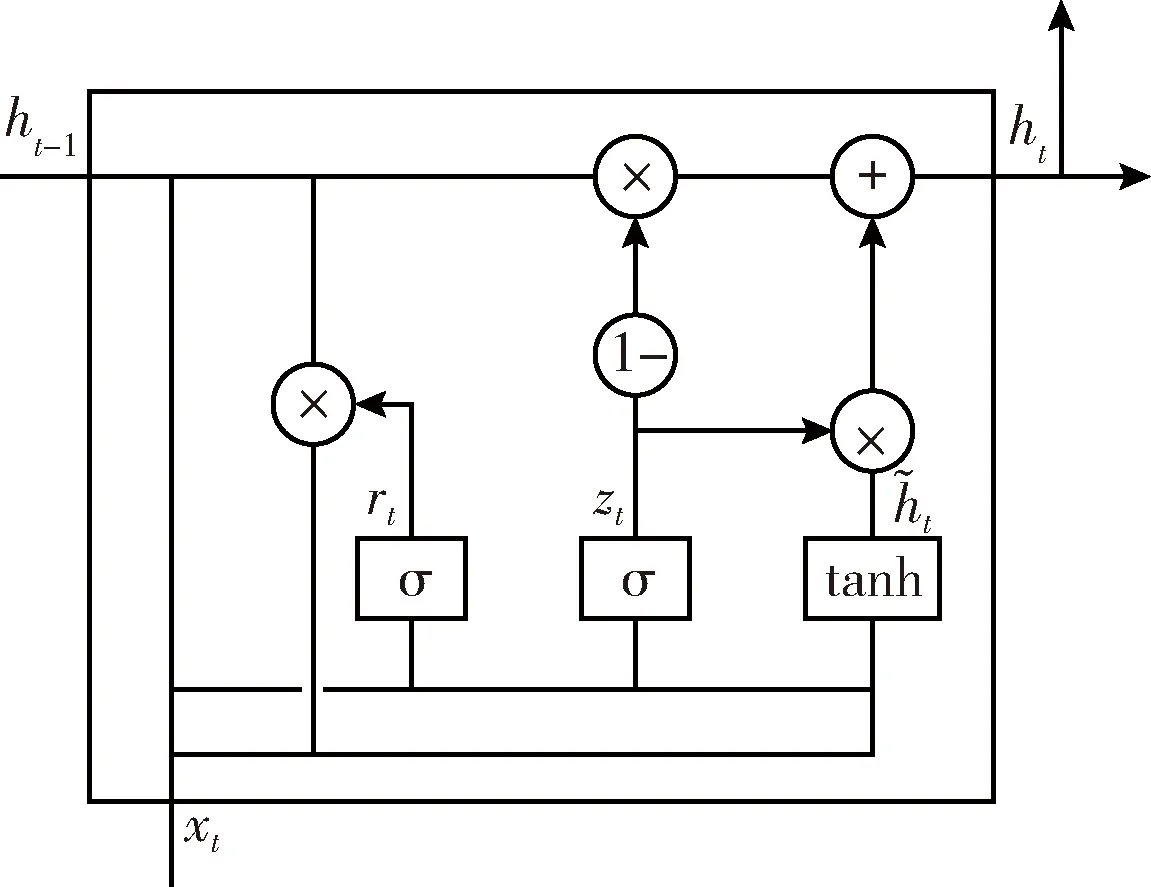
圖3 GRU單元結構

具體前向傳播公式如下

(7)

其中，Wxr為輸入層到更新門的權重矩陣，Whr為隱藏狀態到更新門的權重矩陣，Wxz為輸入層到重置門的權重矩陣，Whz為隱藏狀態到重置門的權重矩陣，Wxh為輸入層到隱藏狀態的權重矩陣，Whh為隱藏狀態之間的連接權重矩陣；br，bz，bh分別為更新門、重置門、隱藏單元的偏置向量。

循環神經網絡相較于普通神經網絡最大的區別就是存在time step(時間步長)參數，GRU也同樣存在這個參數。這個參數的選擇決定了訓練時利用多少步長內的時序關系，即輸出與前多少個陸續的數據輸入有關系。具體GRU和循環神經網絡的結構與推導公式見文獻[14]。

3 GRU循環神經網絡輔助INS/GPS組合導航

目前關于GPS失鎖時使用AI技術進行輔助的模型主要有3種，分別是OINS-δPINS模型、OINS-Xk模型和OINS-ΔPGPS模型，都有著不錯的效果[15]。OINS-δPINS模型輸入為INS信息，輸出為GPS和INS的誤差；OINS-Xk模型輸入為INS信息，輸出為Kalman濾波后的狀態向量；OINS-ΔPGPS模型輸入為INS信息，輸出為GPS增量信息。前兩種模型的預測值既包含INS信息，也包含GPS信息，而第三種模型的預測值僅與GPS信息相關，因此前兩種模型相較于第三種模型會引入額外的混合誤差，所以本文采用OINS-ΔPGPS模型。ΔPGPS的具體推導公式如下

(8)

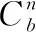
(9)

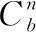
具體工作流程如圖4所示，在GPS信號鎖定時，使用GRU循環神經網絡進行實時訓練，輸入為IMU提供的三軸加速度計數據fb、三軸陀螺儀數據ωb、INS輸出的速度信息VINS和航向角ψINS。因此在GPS信號良好時GRU模塊可以找到IMU、INS信息與GPS增量信息之間的映射關系。

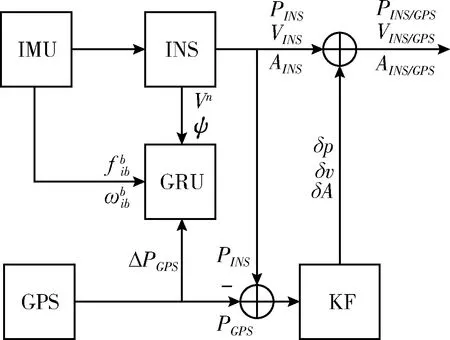
圖4 GRU輔助INS/GPS組合導航訓練過程

當GPS失鎖后，GPS模塊不再提供位置信息，IMU和INS模塊繼續向GRU模塊輸入傳感器數據，慣導推算結果等相關信息，由已訓練好的GRU循環神經網絡根據輸入來預測ΔPGPS。將上述GPS增量信息進行積分，就可以得到一個模擬的GPS位置信息[16]，也叫作偽GPS位置信息，效果等同于GPS信號鎖定時的GPS定位結果。將該結果與PINS作差后送入KF模塊即可繼續進行卡爾曼濾波，用來對位置、速度、姿態進行修正，如圖5所示。此時原本只能通過慣導進行推算的純慣導模塊，有了偽GPS信息對其進行修正，抑制了MEMS級慣導的誤差發散速度。

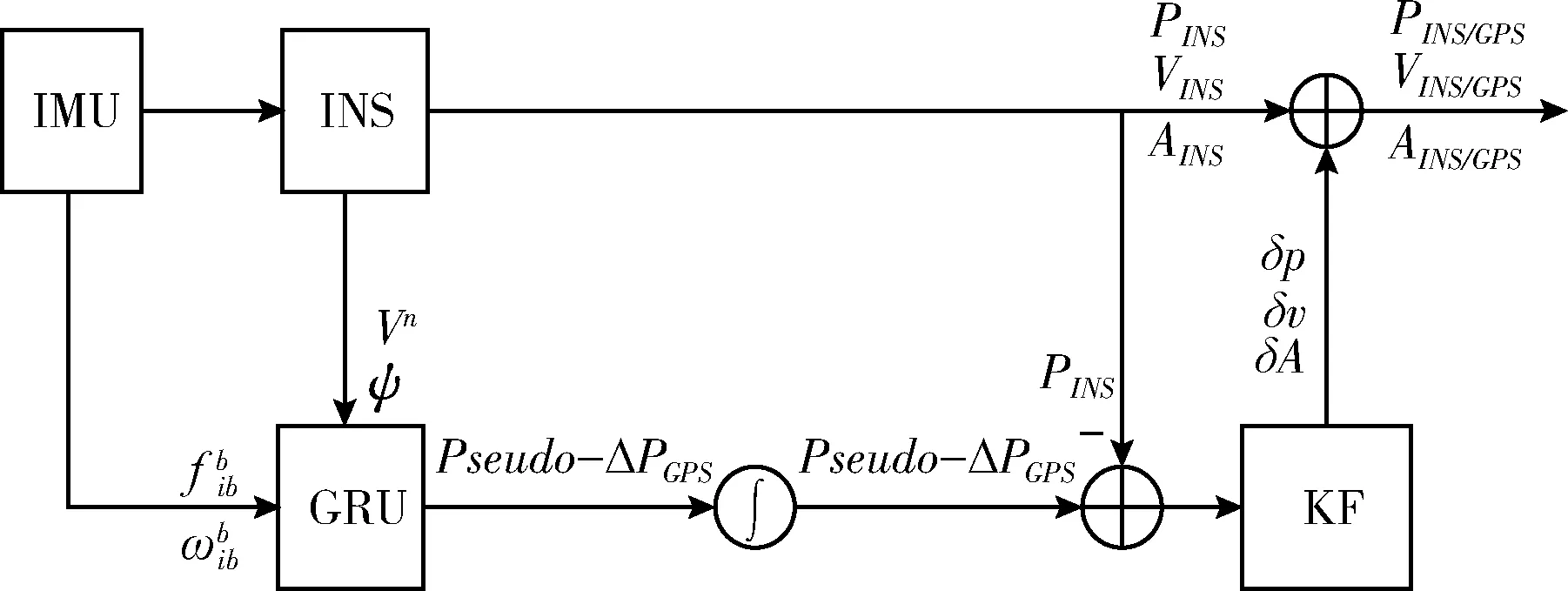
圖5 GRU輔助INS/GPS組合導航預測過程

4 算法驗證

為驗證算法，使用邁普時空的M39設備所采的數據進行仿真，采樣輸出頻率為200 HZ，利用SPAN-CPT設備作為參考系統，二者的IMU性能參數見表1。數據采集地點為武漢市佛祖嶺附近，所采數據共4500 s，選取中段的4000 s數據來進行仿真，前3000 s用于訓練，3000 s-3200 s用于驗證，3200 s-4000 s用于測試。

表1 仿真設備與參考設備的IMU性能參數

GRU模型的輸入為IMU的三軸陀螺儀數據、三軸加速度計數據、速度矢量、航向角共10個特征維度，輸出為GPS增量信息。訓練時由于輸入層的IMU傳感器數據、速度、航向角等INS信息為1 s 200次，而GPS增量信息1 s僅有1次，所以訓練時需要將1 s內的所有信息一起作為輸入層的輸入。進一步地，由于GRU模型存在time step參數，即存在時間上的維度，結合上述的10個特征和信息頻率以及訓練時長為3000 s，因此輸入層的數據為大小為(3000,time step,2000)；而輸出層的數據顯然為GPS增量信息，大小為(3000,3)。此數據量非常龐大，隱藏層的神經元個數，time step的參數選擇都會影響到訓練的效率和最終精度，因此本文先對輸入層和輸出層數據進行了歸一化處理，預測模型預測時再反歸一化，以加快訓練時的收斂速度。并且對于相關參數的調節也進行了實驗，見表2。

表2 不同time step和隱藏層單元數的性能對比

表2中為不同time step和隱藏層單元數的調節情況。考慮到效率和精度，最終本文中GRU模塊優化器選擇為adam算法，隱藏層神經元個數設置為128個，time step參數選擇為4，其它參數變量的值見表3。

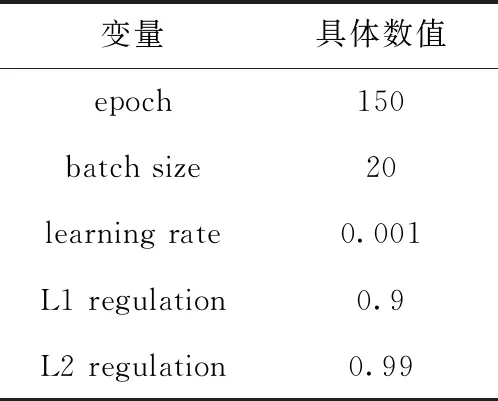
表3 GRU模塊參數設置

由于本文采用的實驗環境為車載環境，高程在精度上的變化與影響較小，因此下述實驗僅考慮和分析水平誤差。圖6、圖7分別為測試集GRU預測的緯度、經度增量和真實的緯度、經度增量的比較，可以看出二者趨勢基本一致。具體的平均絕對誤差(mean absolute error，MAE)和均方誤差(mean square error，MSE)統計見表4。

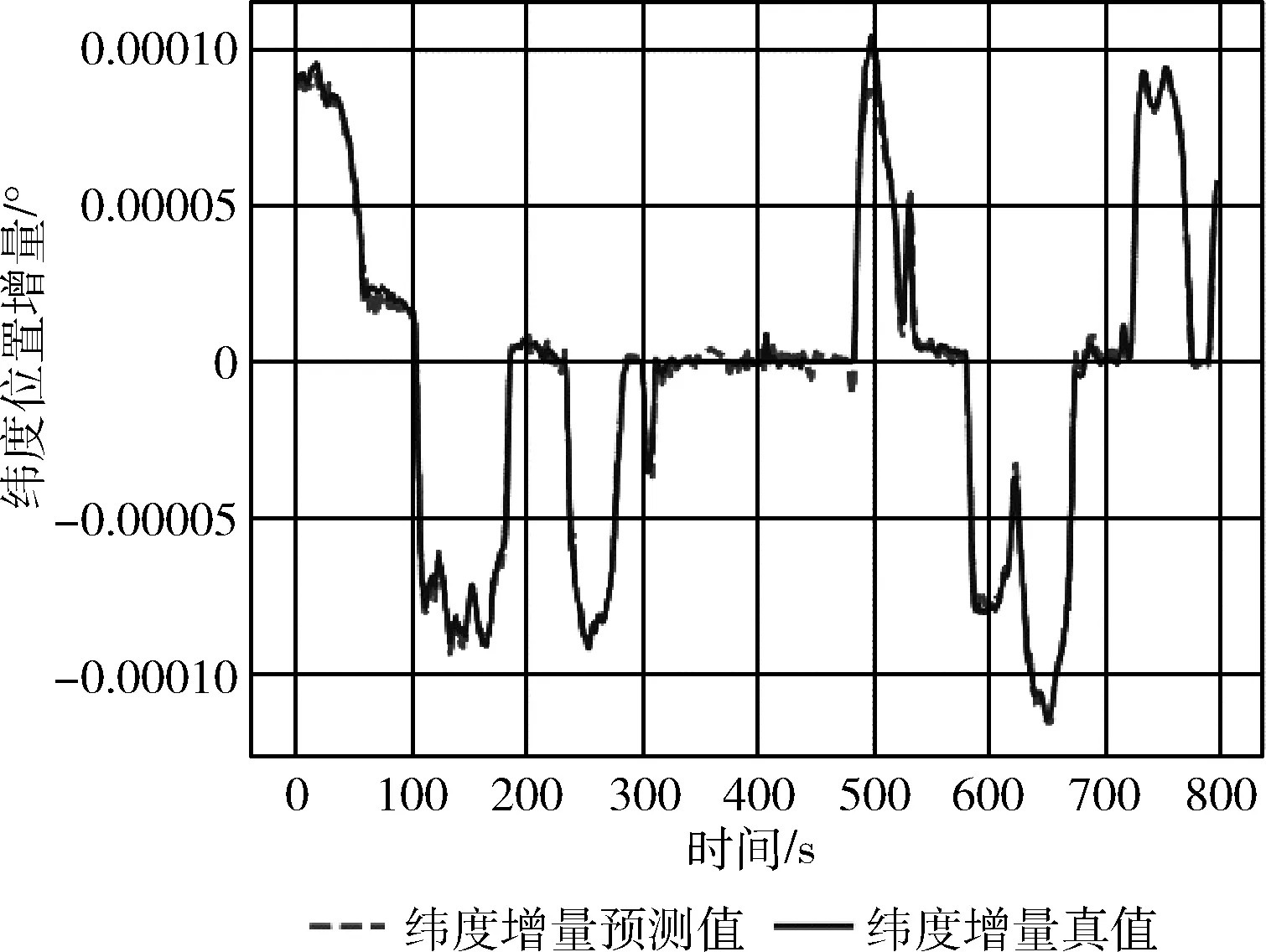
圖6 GRU預測緯度增量與真值的對比

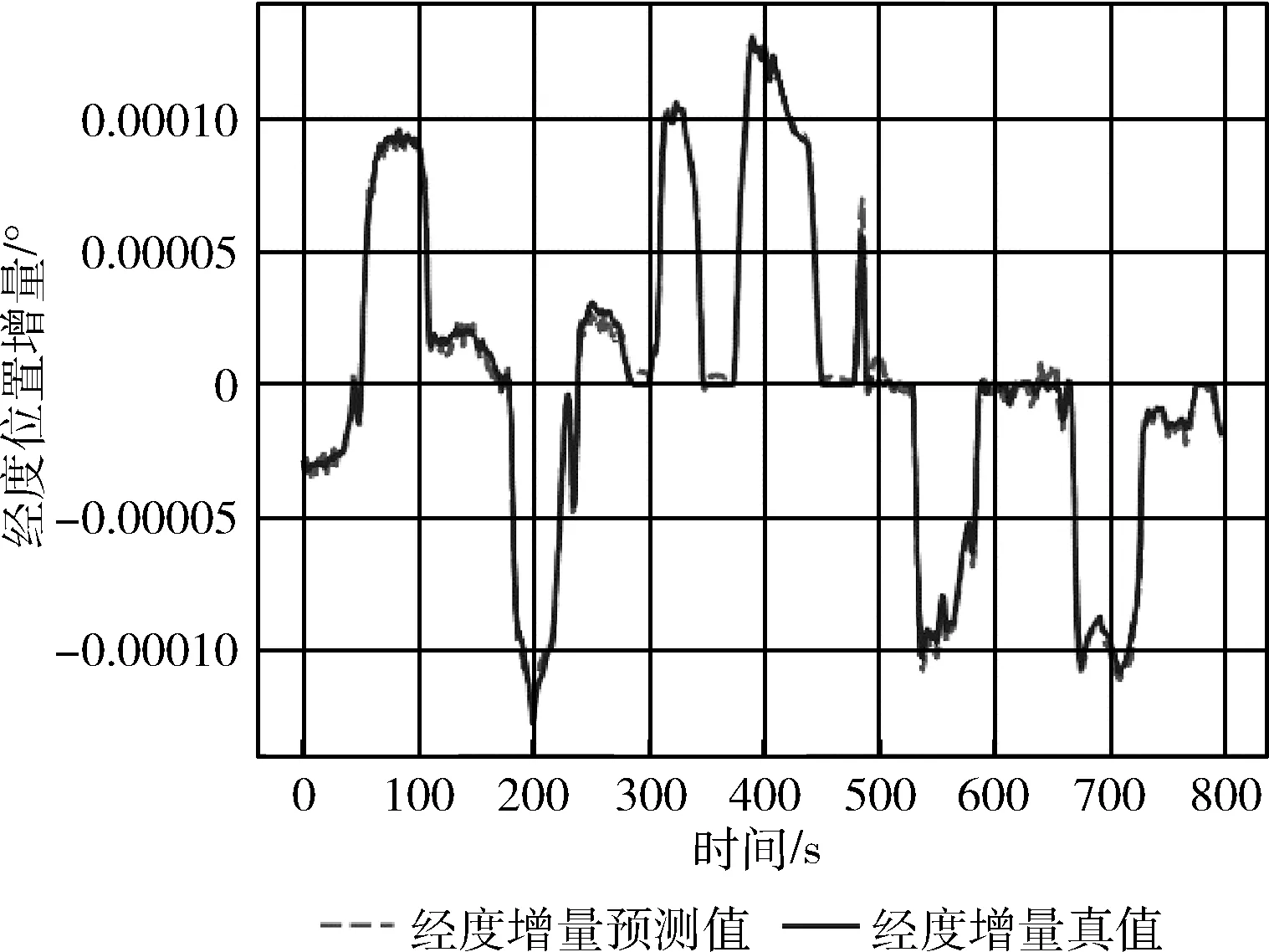
圖7 GRU預測經度增量與真值的對比

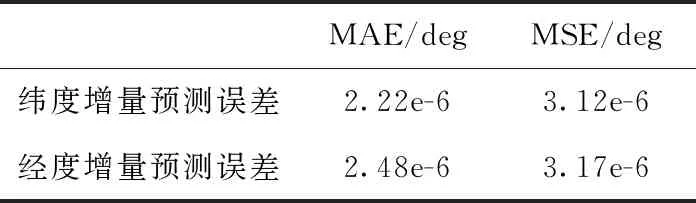
表4 GRU預測的經緯度增量誤差統計

圖8是將800 s預測的ΔPGPS累加畫出的水平軌跡圖與真實軌跡的比較。起點處二者重合，誤差逐漸增大，最大誤差不超過50 m。從圖8中也可以看出，雖然全程誤差都在發散，軌跡逐漸分離，但是誤差陡增的幾處基本為拐彎處，直線行駛時誤差增加很小。這是因為車載環境下直線行駛的情況較多，相應地，訓練集中直線行駛的數據就更豐富，GRU模型更容易找到直線行駛時INS、IMU信息和GPS增量的關系。同時，相較于拐彎，直線行駛時的IMU測得的數據更準，慣導推算結果也更精確，這也導致了上述結果。

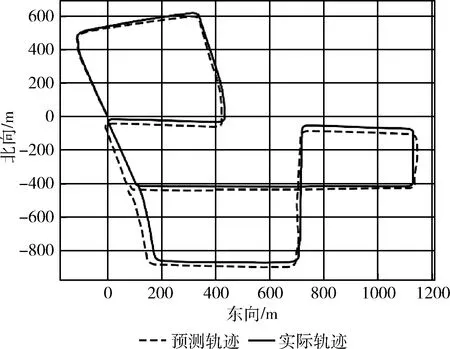
圖8 GRU預測的軌跡與實際軌跡對比

上述仿真是采用了組合導航的結果進行預測，目的是為了驗證GRU模型應用于GPS增量預測時的可行性，并調節GRU網絡的參數，使得該預測模型達到最優；實際使用本模型時，由于一次次的預測會導致速度、航向、位置等信息的誤差累積，因此選取其中200 s(202100 周秒-202300 周秒)的時間完整模擬本模型方法。為了進一步說明GRU循環神經網絡相較于普通神經網絡的優越性，下述圖中還加入了MLP的預測情況。圖9(a)、圖9(b)分別為GPS失鎖200 s時GRU循環神經網絡模型輔助的組合導航與GPS失鎖時純機械編排的北向/東向速度漂移對比。GRU、MLP算法輔助的北向、東向速度漂移要優于純慣導、其中GRU效果更好。純慣導推算北向、東向最大速度漂移分別為4.61 m/s，3.37 m/s；MLP輔助的北向、東向最大漂移分別為4.55 m/s、2.83 m/s，與純慣導推算相當，略小于純慣導結果，但是整體要優于純慣導；GRU輔助的北向，東向最大速度漂移為1.55 m/s，1.17 m/s。GRU輔助相較于純慣導推算，北向和東向最大速度漂移分別降低66.4%和65.3%。GRU輔助相較于MLP輔助，北向和東向最大速度漂移分別降低65.9%和56.7%。

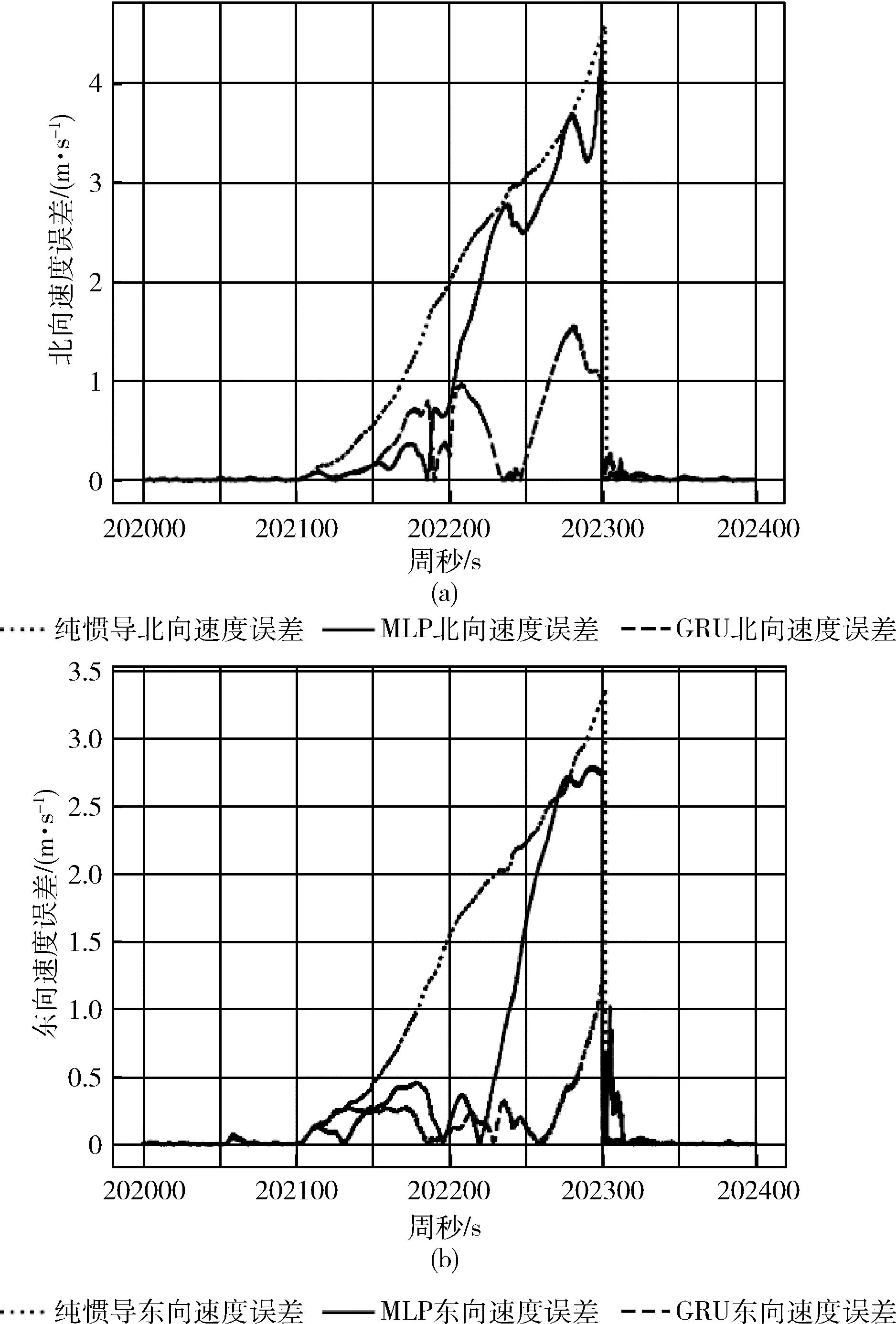
圖9 不同算法輔助的速度漂移

圖10、圖11、圖12分別為GPS失鎖200 s時GRU循環神經網絡模型輔助的組合導航與GPS失鎖時純機械編排的緯度、經度、水平位置漂移對比。純慣導緯度、經度、水平最大漂移分別為394.51 m、294.66 m、492.40 m；MLP輔助的緯度、經度、水平最大漂移分別為370.23 m、166.78 m、406.06 m；GRU輔助的緯度、經度、水平最大漂移分別為86.88 m、69.07 m、87.14 m。GRU輔助相較于純慣導推算、緯度、經度和水平方向最大位置漂移分別降低78.0%、76.6%和82.3%；GRU輔助相較于MLP輔助、緯度、經度和水平方向最大位置漂移分別降低76.5%、58.6%和78.5%。上述所有統計結果總結見表5。

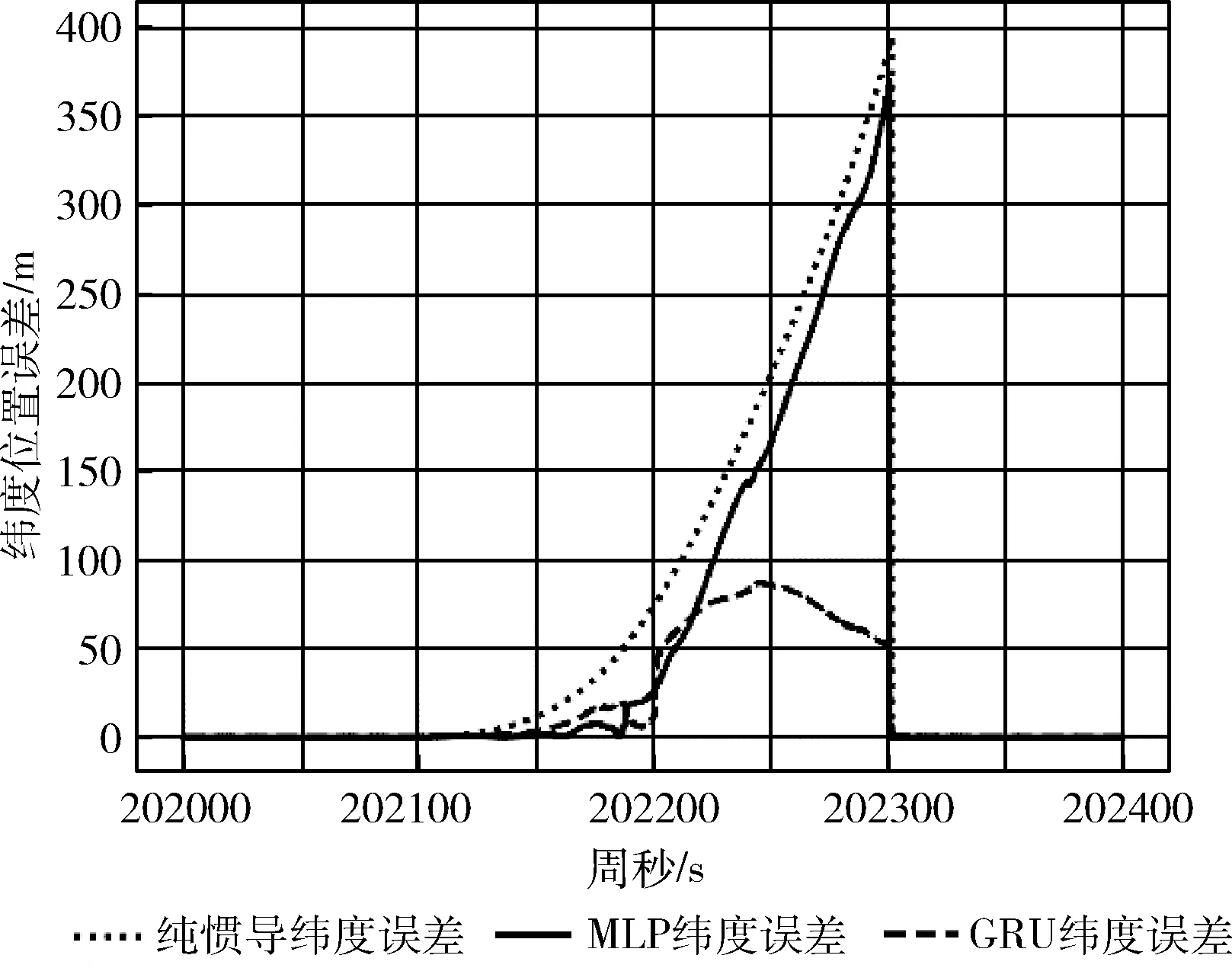
圖10 不同算法輔助的緯度位置漂移

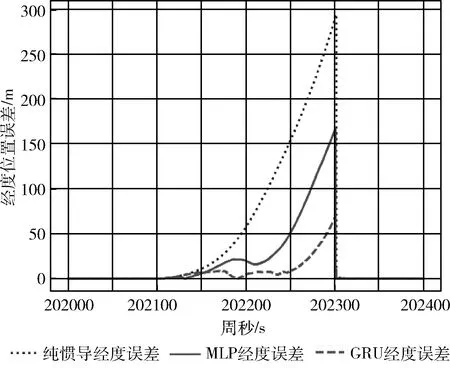
圖11 不同算法輔助的經度位置漂移

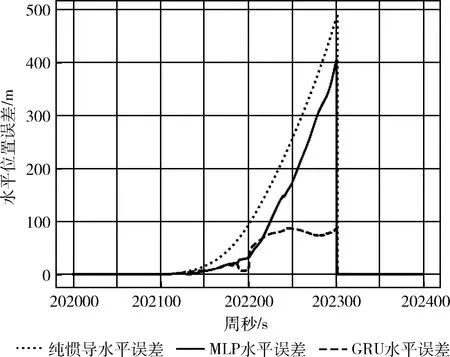
圖12 不同算法輔助的水平位置漂移

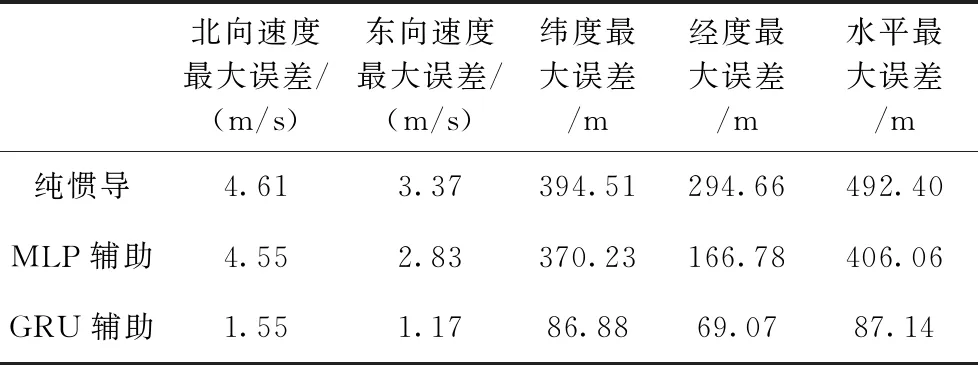
表5 GPS失鎖200 s的3種方法最大誤差統計結果

圖13為這200 s仿真結果在Google Earth上的軌跡。黑色的兩條線分別為真實軌跡和GRU輔助軌跡，其中真實軌跡的圖標為黑色實心圓，GRU輔助軌跡的圖標為黑色正方形；白色的兩條線為MLP輔助軌跡和純慣導軌跡，其中MLP輔助軌跡的圖標為白色空心三角形，純慣導軌跡的圖標為白色空心圓。可以看出經過一個彎道后，3種方法與真實軌跡的誤差已經有了明顯的差距，GRU輔助的最為接近，MLP輔助的次之，純慣導推算最差；經過2個彎道后只有GRU輔助的軌跡仍與真實軌跡趨勢接近，其它軌跡都發散嚴重。

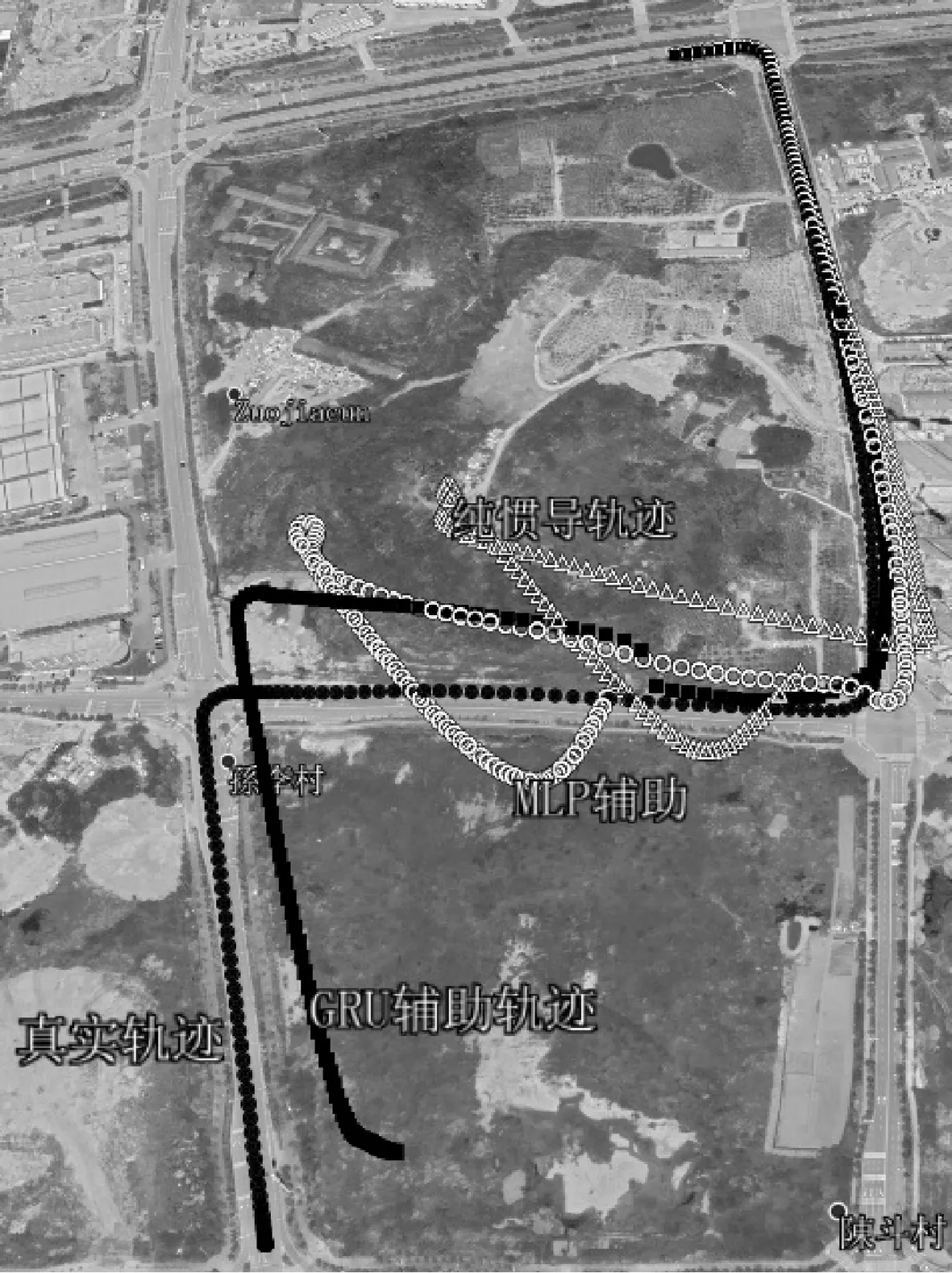
圖13 不同算法輔助的地圖軌跡

表6為GPS失鎖200 s的3種方法RMS統計結果，可以看出使用MLP、GRU輔助的結果各方面都要優于純慣導推算，其中GRU輔助最優，水平誤差54.20 m相較于純慣導的204.80 m和MLP輔助的153.40 m有巨大提升。

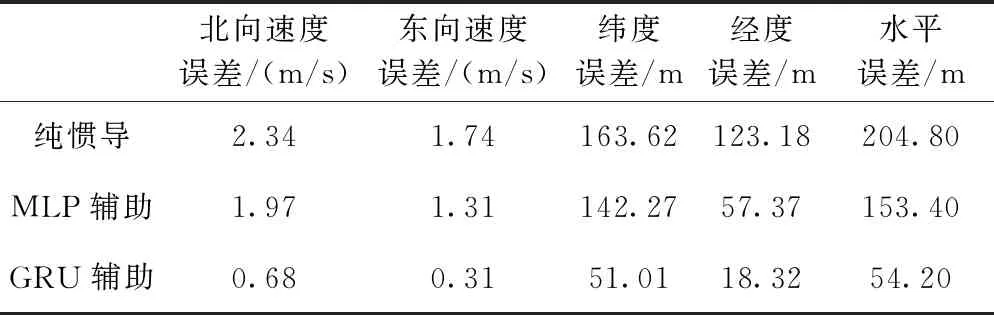
表6 GPS失鎖200 s的3種方法RMS統計結果

5 結束語

本文為了解決GPS失鎖時純慣導推算發散嚴重的問題，采用了GRU輔助INS/GPS的方法。在GPS鎖定時使用INS速度、姿態角信息、IMU加速度計、陀螺儀數據和GPS增量進行訓練，找到相應的映射關系；GPS失鎖后，向訓練好的GRU模型繼續輸入INS和IMU信息，該模型就可以提供預測的GPS增量信息，將之積分得到偽GPS位置。此時就可以進行卡爾曼濾波，以抑制原本純MEMS級慣導推算時的誤差快速發散。并且本文與MLP輔助INS/GPS的方法進行了比較，驗證了GRU循環神經網絡對于連續時間軌跡推算的優越性。由于GPS失鎖時，里程計在車載導航中對精度有著極為明顯的提升，且技術較為成熟，因此，下一步工作將結合里程計與本方法進行進一步實驗。