提高多芯片拼接線性度的新方法
高慧瑩,左 寧,艾 博
( 中國電子科技集團公司第四十五研究所,北京100176)
隨著光學探測技術的發展,感光元件的面積越來越大,精度越來越高,組成感光元件的芯片拼接尺寸越來越小、數量越來越多,尤其當成像尺寸到達15 000 像元的時候,不僅對芯片拼接的單行直線度要求越來越高,且對行與行之間的平行度要求也提出了嚴格的要求。傳統的通過CCD 觀察、手動拼接已遠遠不能滿足要求,迫切需要進行自動拼接、在線測量,以保證芯片拼接的質量及效率。
1 芯片集成拼接工藝流程
芯片集成拼接方法如圖1 所示,主要是為了保證芯片拼接后每一行的直線度和行與行之間的平行度。

圖1 芯片集成拼接示意圖
芯片拼接工藝流程如圖2 所示。拼接主要環節為五步:
(1)通過CCD 觀察進行第一片的拼接,并測量拼接后的芯片上兩個特征點位置坐標;
(2)根據第一片拼接的兩個特征點坐標,結合拼接允許誤差,確定第二片的拼接位置并進行第二片自動拼接,并進行第二片芯片的特征點位置測量;
(3)根據第一片、第二片四個特征點拼接位置,結合拼接誤差確定第三片芯片的拼接位置,并進行測量,以此類推,確定同一行第m個芯片的拼接位置并進行拼接和測量;

圖2 拼接流程示意圖
(4)根據第一行的芯片拼接特征點坐標,進行線性度擬合,確定第一行芯片拼接的直線度,并根據直線度允許誤差,確定第二行第一片的芯片拼接位置,并進行拼接;
(5)按照第二步、第三步的方法,完成第二行的芯片拼接并測量直線度。以此類推,進行第n行芯片的拼接和測量。
2 芯片拼接方法
芯片上選2 個特征點,將2 個特征點坐標分別定義為(xnm1,ynm1),(xnm2,ynm2),其中n代表從上到下的行順序,m代表行內的從左到右的芯片順序。同一行兩片芯片間的間距為a,每一行之間的間距為c。直線度允許誤差定義為(△x1、△y1),平行度允許誤差定義為(△x2、△y2),所有坐標的提取均通過CCD 掃描,圖像識別自動在線提取。
2.1 首片拼接后的處理
在基板上的固定位置將首片芯片拼接粘合后,通過CCD 掃描,圖像識別,得出其上兩個標記點的位置坐標:

通過這兩個坐標擬合出連接這兩點的直線方程式為:

該直線的斜率k為:

該直線的截距b為:
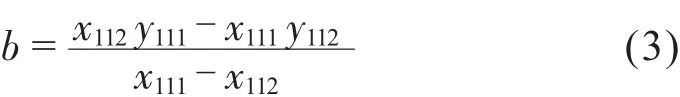
結合兩片芯片間的間距a和可接受的位置誤差△x1、△y1,可以通過如下公式確定出第二片芯片拼接兩個特征點的位置范圍。
(x121,y121)的坐標范圍為:


(x122,y122)的坐標范圍為:
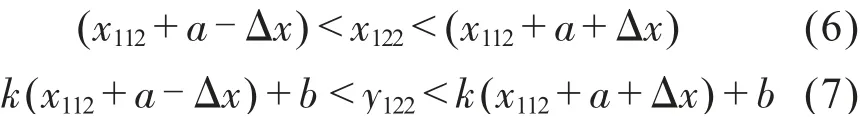
2.2 單行第n+1 片芯片的拼接方法
確定了第二片芯片的拼接位置后控制設備進行拼接操作,拼接后再使用CCD 相機對新拼接好后的芯片進行圖像掃描,從第三片起識別出每一個剛拼接好的芯片上的兩個標識點的具體位置坐標:

通過將前n片芯片上的2n個特征點坐標值代入最小二乘法公式進行計算,即可擬合出一條線性歸回直線方程,其用到的公式見式(8)~式(11):

線性回歸直線方程的表達式為y=kx+b,其中參數k為該條直線的回歸系數,可以用其描述該直線的傾斜程度,b為截距。要求出公式中的參數k和b,可以使用公式(12)、(13)進行計算:

繼續通過間距a和位置誤差范圍△x、△y,即可通過以下公式確定出第n+1 個芯片拼接的兩個特征點位置。
(x1(n+1)1,y1(n+1)1)坐標范圍為

(x1(n+1)2,y1(n+1)2)坐標范圍為:
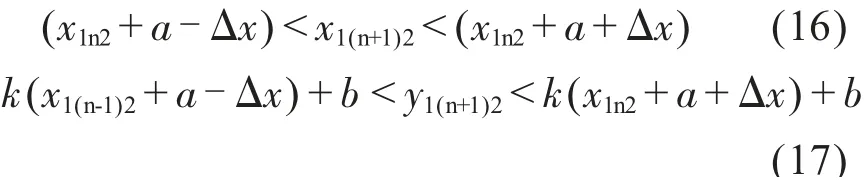
2.3 第n 行芯片的拼接方法
在拼接完成上一行的芯片后,通過將兩行芯片之間的垂直位置間距c代入計算方法,即可求得該行首片芯片第一個標記點的粘接坐標(xn11,yn11)。為了保證每行芯片的平行度達標,將坐標(xn11,yn11) 和上一行的線性回歸直線方程中的斜率k代入的表達式y=kx+bn中,即可求得參數bn的值如式(18):

將兩標記點之間的距離d引入,即可求出該行首片芯片的第二個標記點坐標(xn12,yn12)式為:

通過計算得出的該行首片兩標記點坐標,即可得出其拼接具體位置。拼接完成首片后,采用和單行拼接時首片拼接后的處理同樣方法來拼接第二片(同前述2.1 節),配合CCD 圖像掃描,從第三片起,使用反復迭代擬合直線的方式來對該行剩余芯片進行拼接(同前述2.2 節)。第n行芯片拼接流程如圖3 所示。
3 拼接后直線度平行度檢測
處理坐標數據擬合曲線的方法有多種,我們遵循設備工藝特點采用了最小二乘法來對每組坐標數據進行擬合,求出其線性回歸方程,通過分析該線性方程,即可比對出拼接后芯片的幾何位置直線度以及平行度。
獲得了每條直線方向拼接后芯片的位置坐標數據后,將每組坐標數據通過最小二乘法進行擬合求出其線性回歸方程。
通過計算得出拼接后芯片位置的線性回歸方程后,即可用以下方法計算求出芯片拼接的直線度和平行度:
直線度:對每一組坐標擬合出的直線進行擬合計算,如果第一個標識和最后一個的垂直位置相差在直線度允許范圍內,則該水平方向上的芯片拼接直線度符合要求,反之亦然。

圖3 多行芯片拼接流程
平行度:將兩組坐標數據擬合出的線性回歸方針的斜率k、k′進行對比,其誤差在平行度允許范圍內為拼接平行度合格,反之亦然。
在直線度、平行度的檢測過程中,我們設定直線度、平行度的范圍為±5 μm。
3.1 芯片水平位置檢測
通過內置模塊的自動計算處理,即可快速檢測出芯片拼接水平位置的放置誤差,并且實時傳遞給拼接設備對其進行校準,高效可靠。如下圖所示為使用通過圖像獲取到的坐標數據來計算直線度和平行度的算法流程。
3.2 檢測方法
對涉及的算法進行編程,最終求出線性回歸方程y=ax+b。
程序代碼中的變量dSumX、dSumY為識別點x、y坐標的和,dMeanX、dMeanY為識別點x、y坐標的平均值,通過對每一個識別點的x、y坐標分別進行累加后處理求得:

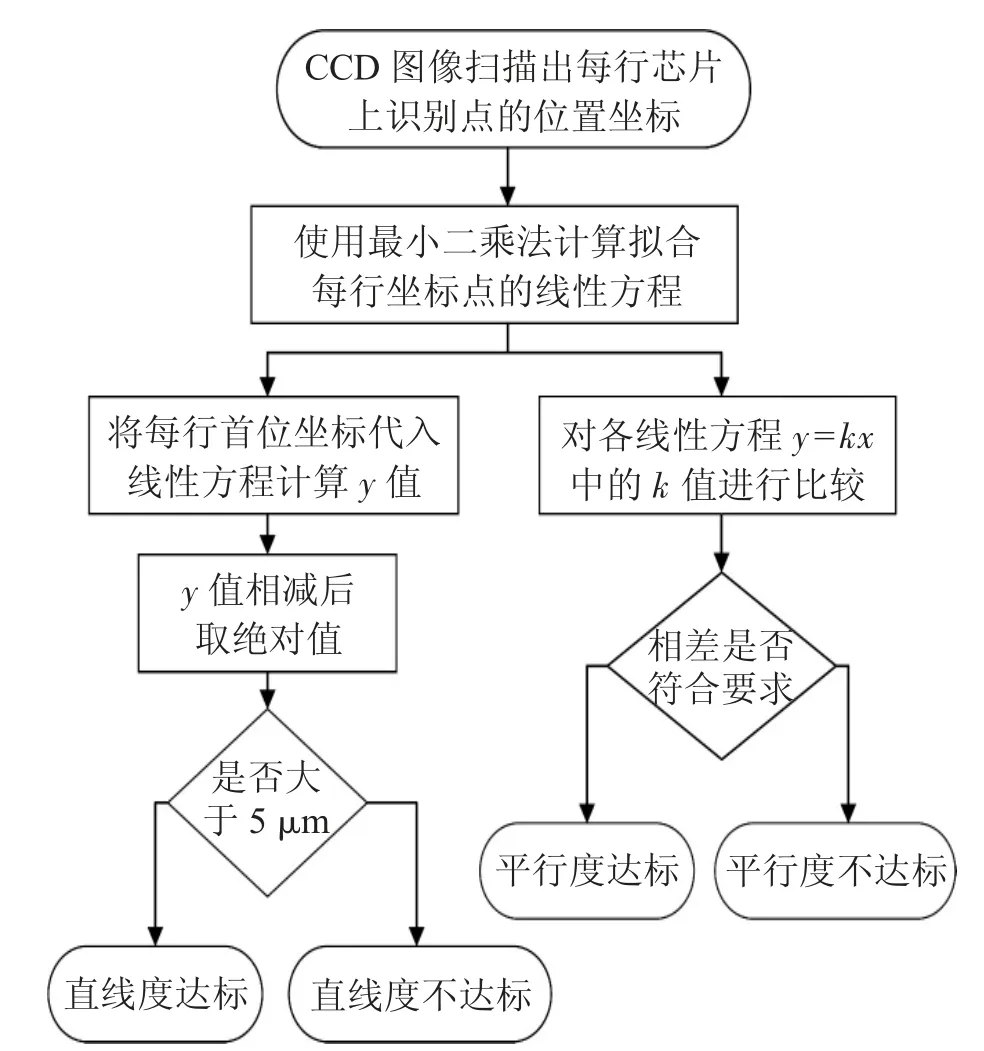
圖4 計算直線度和平行度算法流程
求得所有參數后,將最小二乘法求線性回歸方程的公式通過代碼實現,即可求得線性方程的斜率a以及截距b:
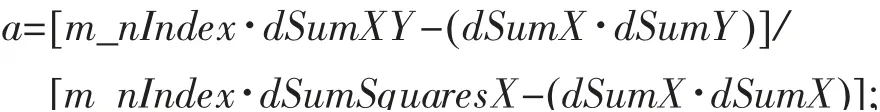
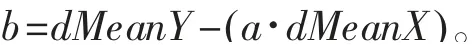
4 檢測算法仿真分析
為了驗證上述方法的可行性,通過CCD 提取拼接后需要檢測的2 行,每行各15 個特征點的位置坐標,數據如表1 所示。
利用特征點散點位置坐標,通過最小二乘法擬合出如圖5 所示的擬合直線,并得出線性回歸方程分別為:

分析圖5 中的2 條擬合直線及其方程,可見第一行在垂直方向的誤差為3.2,線性回歸方程斜率為0.058。第二行垂直方向的誤差為2.1,線性回歸方程斜率為0.038。假定設定的直線度誤差閾值為5,則該次拼接的直線度達標。將方程1 和方程2 的斜率進行對比即可求得其平行度數值。假定設定的平行度斜率差不能超過0.05,則模擬的兩行芯片因其拼接各自的線性回歸方程斜率差為0.02,則可判定其平行度達標。

表1 CCD 提取位置坐標數據表

圖5 仿真計算平行度
5 結束語
通過智能化、自動化的拼接方式解決手動拼接中的誤差過大、一致性不好、效率低等工藝問題已成為光學檢測領域多芯片拼接的主要發展趨勢。本文采用位置坐標擬合,拼接預定位等方法實現多芯片自動拼接,提升了芯片拼接的線性度,并通過仿真分析和實例驗證,證明該方法可有效提升芯片的拼接精度,確保拼接直線度、平行度在可控誤差范圍內。

