初始滲流場對渣土場邊坡降雨入滲特征及其穩定性的影響

李丞，蔡立明，張偉鋒，侯建香，董凱，蘇立君,2,3,4

(1.中國科學院 山地災害與地表過程重點實驗室；中國科學院、水利部成都山地災害與環境研究所，成都 610041；2.中國科學院 青藏高原地球科學卓越創新中心，北京 100101；3.中國-巴基斯坦地球科學聯合研究中心，巴基斯坦 伊斯蘭堡；4.中國科學院大學，北京 100049；5.北京航天控制儀器研究所，北京 100854；6.深圳信息職業技術學院，廣東 深圳 518127；7.深圳市城市公共安全技術研究院有限公司，廣東 深圳518000)

隨著城市化進程的加快，產生了以大量廢土和廢渣為主的余泥渣土，對城市固體廢棄物的管理和城市規劃提出了挑戰[1]，而填埋是最常見的渣土處理方法[2]。對于渣土場邊坡而言，其穩定性受填料性質、施工工藝、降雨、地下水位等影響[3-4]，在眾多因素中，降雨入滲將導致渣土場邊坡含水率增加、基質吸力降低和地下水位上升，這是渣土邊坡變形與穩定性下降的主要原因之一[5-7]。

降雨作用下渣土場邊坡的滲流特征和穩定性的研究主要集中在幾個方面：1)降雨強度和初始含水率對滲濾液產量的影響[8-9]；2)降雨模式和降雨強度對邊坡水分運移及其穩定性的影響[10-11]；3)降雨模式和降雨強度對填埋場覆蓋層滲流特性的影響[12-13]；4)降雨強度對渣土場邊坡變形破壞特征的影響[14-15]。以上成果對于理解渣土場邊坡的水分運移規律和穩定性計算起到了關鍵的作用。然而，上述研究鮮有涉及初始滲流場對渣土場邊坡降雨入滲機制的影響。值得注意的是，在常規邊坡的研究中，學者們分析了初始滲流場對降雨作用下邊坡滲流特征和穩定性的影響[16-18]。其中，唐棟等[17]研究了不同初始滲流條件對不同土體邊坡穩定性的影響，結果表明，初始滲流條件對邊坡安全系數影響很大，并建議將多年平均降雨量對應的穩態滲流場作為初始滲流條件。何忠明等[19]比較了4類初始滲流場對邊坡降雨入滲過程的影響，發現初始滲流場分布形式對降雨過程中邊坡表面孔隙水壓力的影響較小，且初始基質吸力越大，受到降雨入滲的影響程度則越小。然而，由于填筑材料的差異性，渣土場邊坡的降雨滲流特征和穩定性分析較常規邊坡復雜[14,20-21]，因此，初始滲流場對渣土場邊坡降雨入滲和穩定性計算的影響值得深入研究。

筆者以深圳市部九窩渣土場邊坡為研究對象，結合室內土工試驗及實際降雨資料，采用數值分析方法，在探討不同初始滲流場和不同降雨強度對渣土場邊坡的滲流特征影響的基礎上，研究了渣土場邊坡的安全系數變化規律。

1 計算原理

1.1 非飽和滲流原理

邊坡降雨入滲過程可認為是典型的飽和-非飽和滲流過程，通常認為，在非飽和狀態下達西定律依然適用，介質水力傳導度是含水率的函數，Richards等[22]建立了土體中液體瞬時流動的二維控制方程

(1)

式中：hm為基質吸力水頭，m；k(hm)為非飽和土滲透系數，m/s；C(hm)為比水容量，無量綱。

巖土體的滲透系數與土體體積含水率以及基質吸力相關，為了描述這三者之間的關系，通常需繪制土水特征曲線以及滲透系數曲線來說明。目前，確定土體滲透系數經常用到的方法是結合室內試驗結果和經典公式[23]

(2)

kw=ks·

(3)

式中：ua為孔隙氣壓力，kPa；uw為孔隙水壓力，kPa；θw為不同基質吸力條件下土體體積含水率，無量綱；θs為土體飽和體積含水率，無量綱；θr為殘余體積含水率，無量綱；α為土體達到進氣值時基質吸力的倒數，無量綱；n為孔隙尺寸分布參數，無量綱；ks為飽和滲透系數，m/s；kw為不同基質吸力條件下的滲透系數，m/s。

1.2 非飽和土強度理論

在考慮基質吸力的滑坡穩定性分析中，采用非飽和土抗剪強度理論對安全系數進行分析，它是莫爾-庫侖模型的一個擴展模型

τ=c′+(σ-ua)tanφ′+(ua-uw)tanφb

(4)

式中：c′為有效粘聚力，kPa；φ′為有效內摩擦角，(°)；σ為總法向應力，kPa；ua為孔隙氣壓力；uw為孔隙水壓力，kPa；ua-uw為基質吸力，kPa；τ為非飽和土抗剪強度，kPa；φb為隨基質吸力變化的內摩擦角，(°)。

2 有限元模型及計算方案

2.1 工程實例概況

選取深圳市部九窩人工渣土場邊坡作為研究對象，依據壓實度和施工工藝不同，可劃分為3個區：渣土區(壓實度為80%，坡比為1∶1.275)、填埋嚴控區(壓實度為85%，坡比為1∶1.25)和壩體區(壓實度為90%，坡比為1∶1.25)，圖1為渣土場邊坡2017年12月的平面圖。研究場地屬于亞熱帶季風氣候區，年平均溫度22 ℃，年平均降雨量1 900 mm，降水量集中在三月到九月。

圖1 深圳市部九窩渣土場邊坡平面圖Fig. 1 Top view of municipal solid waste landfill in

2.2 邊界條件及計算模型

根據工程地質調查確定圖1中的AB斷面為計算采用的剖面，剖面圖如圖2所示。采用理想彈塑性模型和Mohr-Coulomb屈服準則在Geo-studio中建立數值分析模型[24]，模型共劃分13 232個節點和13 250個單元。在模型中設置監測截面1、2、3，每個截面的高度為8.8 m，其中，在監測截面1和2坡面處各有一個監測點，在監測截面3坡面處設置監測點3，在離監測點3的豎直方向4.4 m處設置監測點4，各監測截面和監測點用來監測邊坡在降雨過程中的滲流特征，監測方案如圖2所示。初始地下水位位于巖土分界面，地下水位線以上土體處于飽和-非飽和狀態。在降雨滲流計算中，定義坡面為單位流量邊界以模擬降雨入滲過程，同時，保證兩側和底部為不透水邊界。

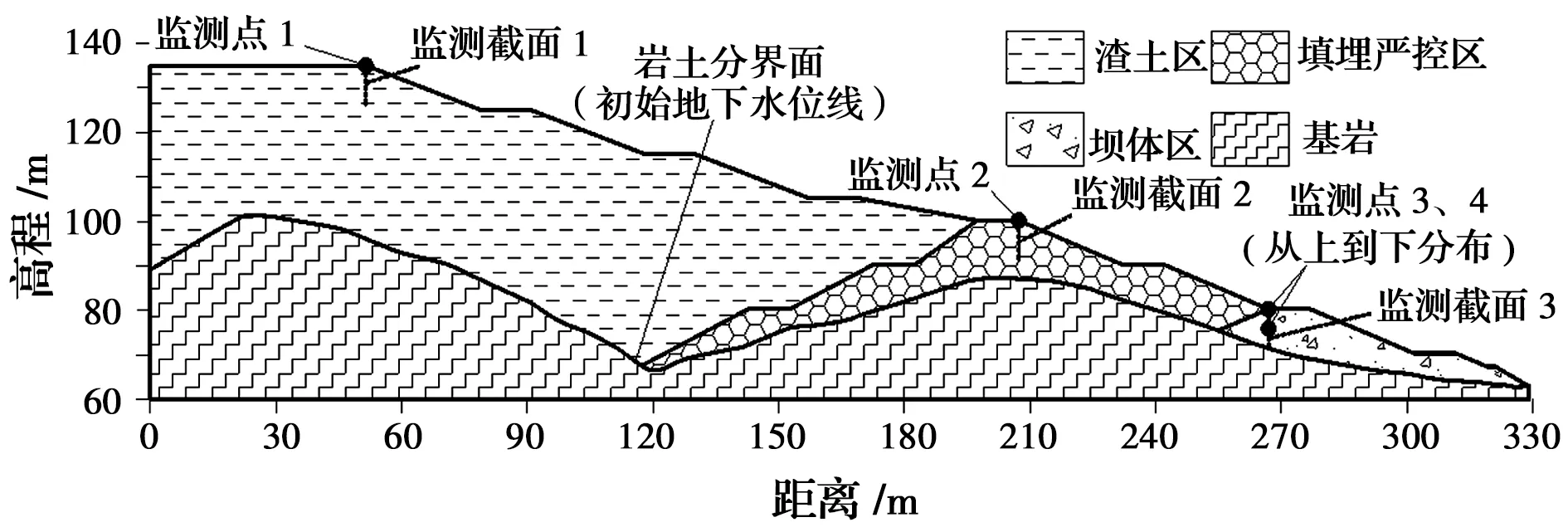
圖2 模型剖面圖和監測點布置Fig.2 Model section and layout of monitoring

根據室內土工試驗所得結果，測得各巖土體的飽和滲透系數值和飽和體積含水率，并用式(2)和式(3)所示VG模型擬合得到巖土體非飽和滲透系數與基質吸力的關系曲線，如圖3所示。此外，當土體的體積含水率達到其自身飽和體積含水率的90%時，則認為土體已經達到飽和狀態[19]，因此，沒有特別說明時，體積含水率大于或等于飽和含水率的90%的區域均視為飽和區范圍，即暫態飽和區(Transient Saturated Zone，簡稱TSZ)。巖土體物理力學參數見表1。

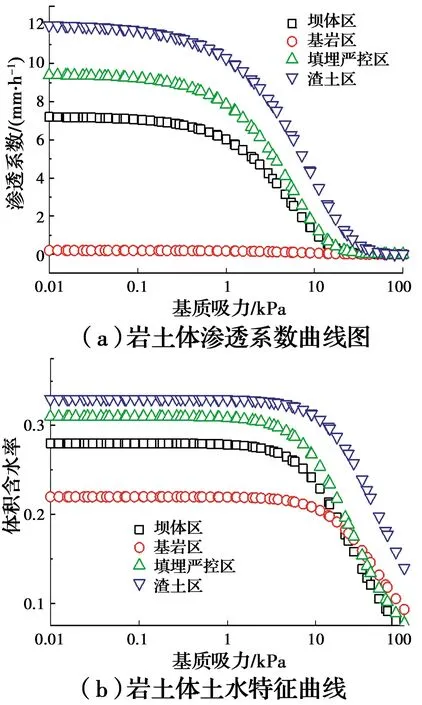
圖3 巖土體水力學參數Fig.3 Hydraulic parameters of rock and

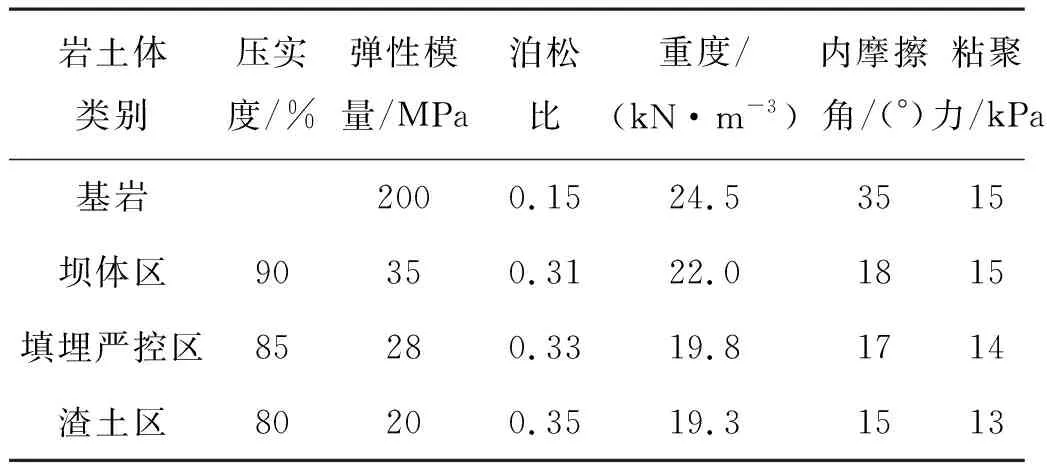
表1 巖土體物理力學參數Table 1 Physical and mechanical parameters of rock and soil

2.3 計算方案

結合深圳地區區域氣象條件，設計了如表2所示的3種工況。由于直接測定坡體內的初始基質吸力分布比較困難，而且費時費力[16]，為了研究初始滲流條件對邊坡滲透特性和穩定性的影響，參考前人研究[16-19]，假設地下水位以上土體基質吸力呈線性增加，達到吸力上限后保持常數。假設坡體內基質吸力上限分別為-25、-50、-75 kPa，并通過微小降雨量形成穩態滲流達到上限值[25]，將穩態滲流形成的基質吸力作為初始滲流條件，如圖4所示。3種工況在進行降雨入滲瞬態分析時均設置3種降雨強度q1、q2和q3，以此研究不同降雨強度下初始滲流場對邊坡降雨入滲特征和穩定性的影響。

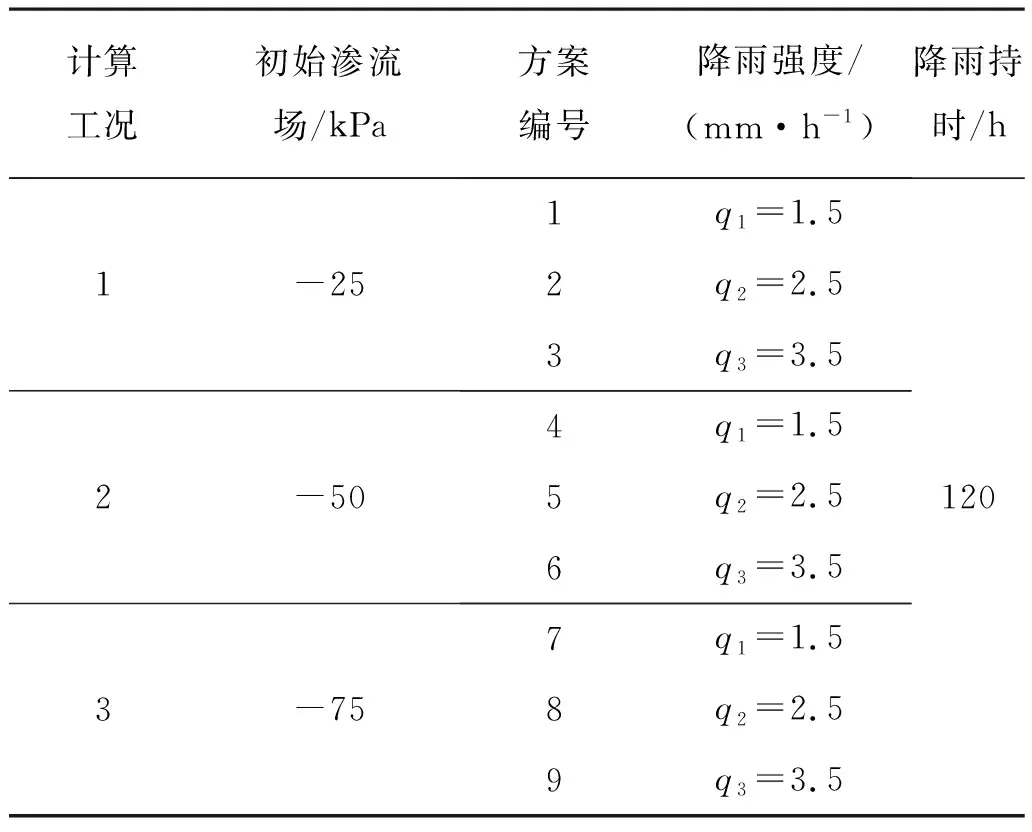
表2 計算方案Table 2 Calculation scheme

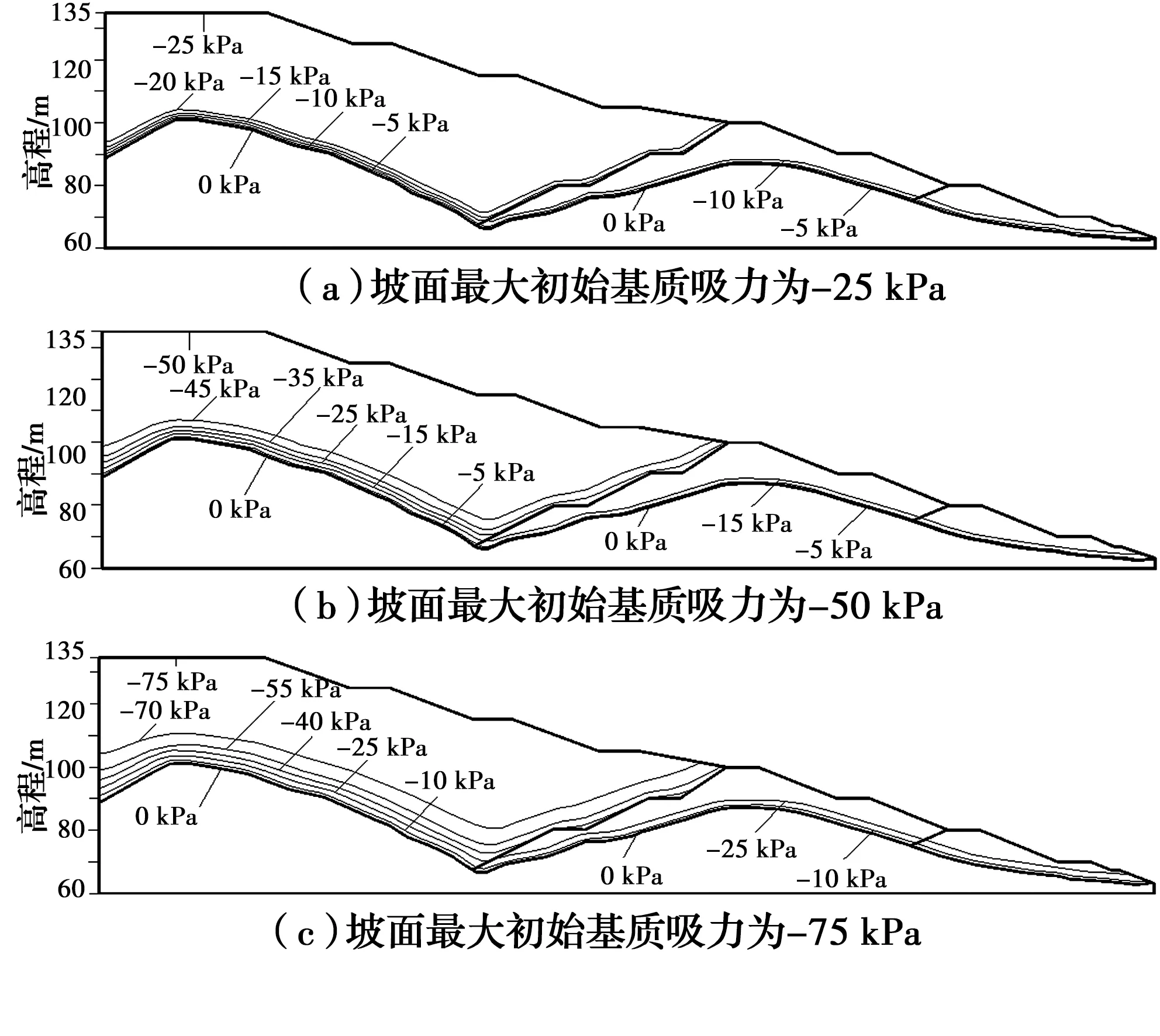
圖4 邊坡初始滲流場分布Fig.4 Initial seepage field distribution of

3 結果與分析

3.1 邊坡監測點流速變化規律

當降雨強度為q1～q3(1.5～3.5 mm/h)和不同初始滲流場時，監測點1、2、3處Y方向流速隨降雨持時的變化關系如圖5所示。由圖5可知，監測點1、2、3的流速均是先增大后減小，最后略大于降雨強度，且同一情況下，監測點2的流速最大，監測點3的流速次之，監測點1的流速最小；對于同一初始基質吸力和監測點，降雨強度越大，流速的峰值越大，且達到峰值的時間越短；對于同一降雨強度和監測點，初始基質吸力越大，流速的峰值越大，且達到峰值的時間越長。此外，當初始基質吸力為-25 kPa時，降雨強度越小，各監測點間流速的數值差距越小，而當初始基質吸力減小至-75 kPa后，各監測點間流速的數值差距越大。

3.2 邊坡監測點暫態飽和區形成時間規律

當降雨強度為q1～q3(1.5～3.5 mm/h)和不同初始滲流場時，監測點1、2、3處的體積含水率隨降雨持時的變化關系如圖6所示。由圖6可知，對于同一初始基質吸力和監測點，降雨強度越大，體積含水率上升速度越快，達到飽和的時間越短，降雨強度越小，暫態飽和區形成的時間越長，甚至不會出現暫態飽和區，以圖6(a)中的監測點1為例，監測點1在q2和q3時達到飽和的時間分別為29、10.9 h，而在q1時沒有達到飽和；對于同一降雨強度和監測點，初始基質吸力越大，體積含水率上升速度越慢，達到飽和的時間越長，以圖6中的監測點1為例(降雨強度q3)，監測點1在初始基質吸力為-25、-50、-75 kPa時達到飽和的時間分別為10.9、20.2、25.5 h。

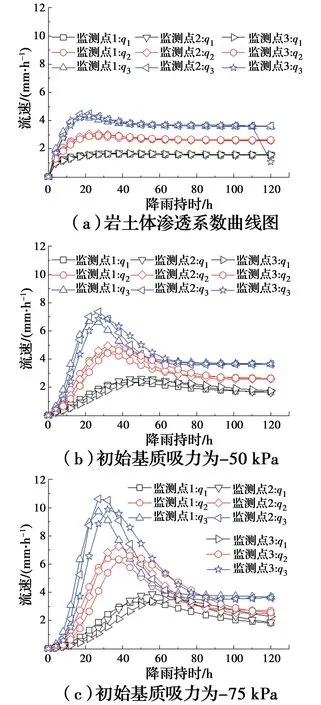
圖5 監測點1、2和3的Y方向流速變化Fig.5 Velocity changes in Y direction at monitoring

圖7為當降雨強度為q3時，不同深度監測點的體積含水率和Y方向流速的變化。由圖7可知，斜坡表面監測點(監測點3)的流速與體積含水率變化要快于坡體內部的監測點(監測點4)，表明暫態飽和區從坡表向坡內擴展；對監測點3而言，體積含水率隨著流速的增加而緩緩增大，當流速達到峰值時，體積含水率也達到絕對飽和(28%)，隨后流速開始下降，體積含水率開始保持不變。值得注意的是，監測點3在120 h時的流速和體積含水率發生了突變(A點和B點)，這是由于降雨導致了地下水位大幅度上升，且地下水已經淹沒了監測點3。

3.3 邊坡暫態飽和區形成深度規律

當降雨強度在q1～q3(1.5～3.5 mm/h)和不同初始滲流場時，監測截面1、2、3處的暫態飽和區深度隨降雨持時的變化關系如圖8所示。由圖8可知，對于同一初始基質吸力和監測截面，降雨強度越大，暫態飽和區深度越大；對于同一降雨強度和監測截面，初始基質吸力越小，入滲深度越大，截面處暫態飽和區出現的范圍越大，體積含水率變化范圍越小，體積含水率在同一位置增大的幅度也越大。此外，當降雨強度為q1時，截面1和2都沒有產生暫態飽和區，截面3的暫態飽和區深度也較小，最大值僅為1.15 m，而當降雨強度為q3時，截面3的暫態飽和區深度最大值卻達8.79 m，由此可見，降雨強度會顯著影響邊坡是否會出現暫態飽和區，而初始基質吸力則會對暫態飽和區深度的數值產生影響。

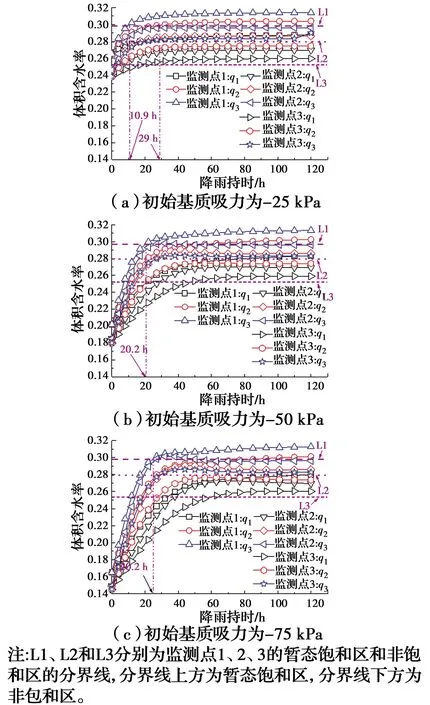
圖6 監測點1、2和3的體積含水率變化Fig.6 Change of volumetric moisture content at monitoring points 1, 2 and

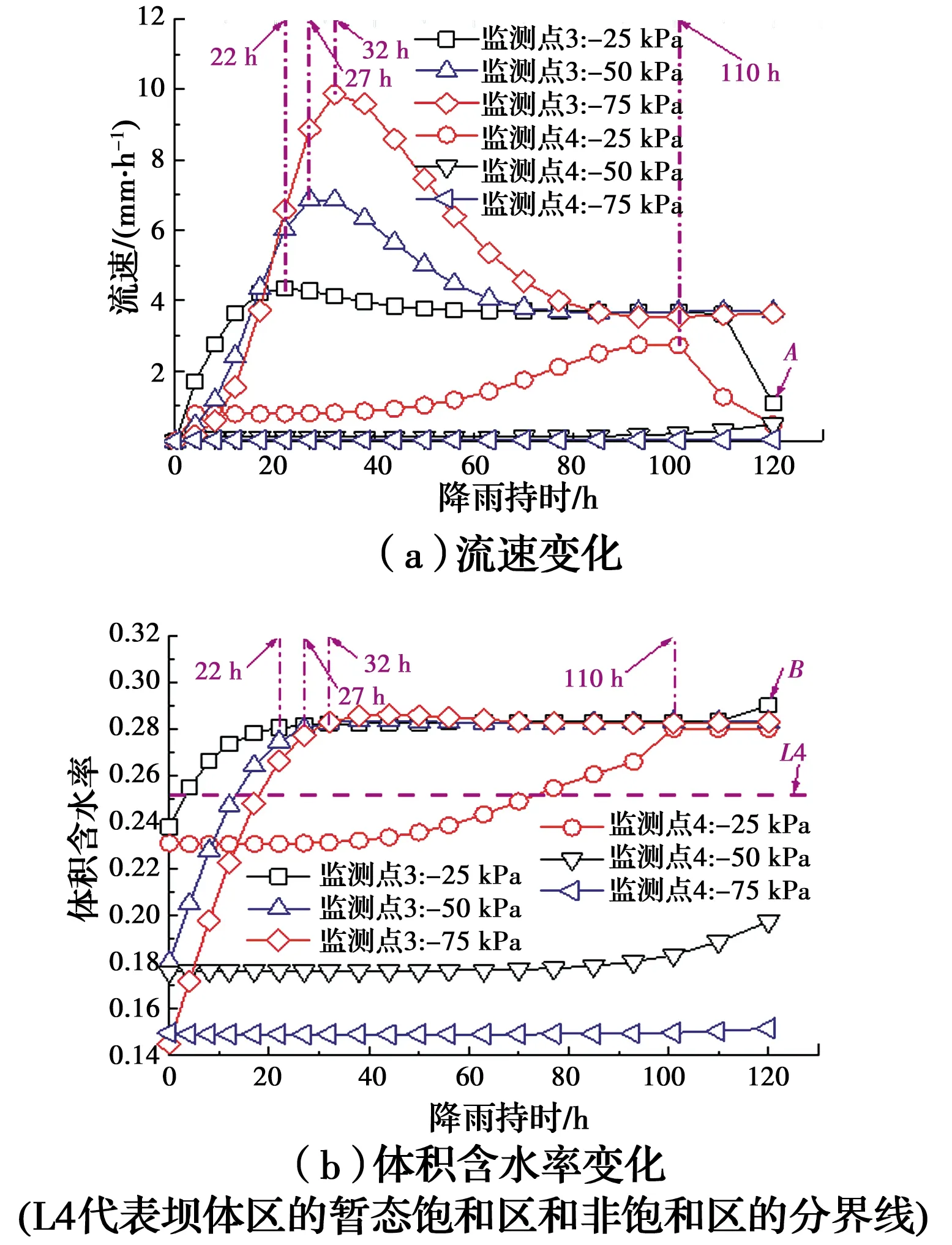
圖7 監測點3和4的體積含水率與流速變化Fig.7 Volume moisture content and flow rate change of

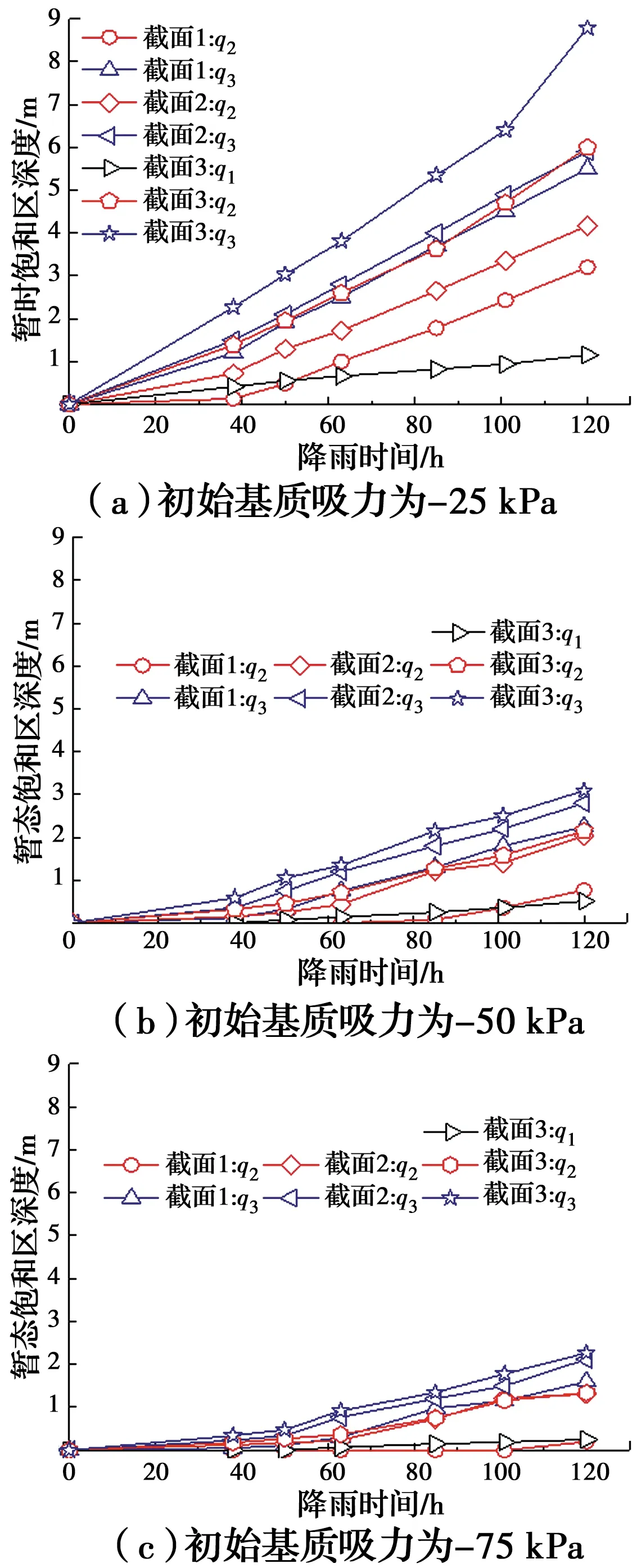
圖8 監測截面1、2和3的暫態飽和區深度變化Fig.8 Monitoring the depth variation of transient saturation zone at Sections 1, 2 and

3.4 邊坡孔隙水壓力變化規律

當降雨強度為q1～q3(1.5～3.5 mm/h)和不同初始滲流場時，監測點1、2、3處的孔隙水壓力隨降雨持時的變化關系如圖9所示。由圖9可知，隨著降雨時間的持續，坡面孔隙水壓力出現了升高的趨勢。具體表現為：對于同一初始基質吸力和監測點處，降雨強度越大，入滲深度越大，孔隙水壓力上升速率越快，降雨結束后的孔隙水壓力也越小；對于同一降雨強度和監測點處，初始基質吸力較大的邊坡孔隙水壓力上升速率快于初始基質吸力較低的邊坡，同時，坡面孔隙水壓力升高速率整體上逐漸減小并趨于水平，就降雨持續時間內孔隙水壓力的數值而言，初始滲流條件對各情況下降雨結束后的孔隙水壓力的影響較小。由此可見，降雨強度會顯著影響孔隙水壓力增長的快慢，而初始基質吸力影響較小。

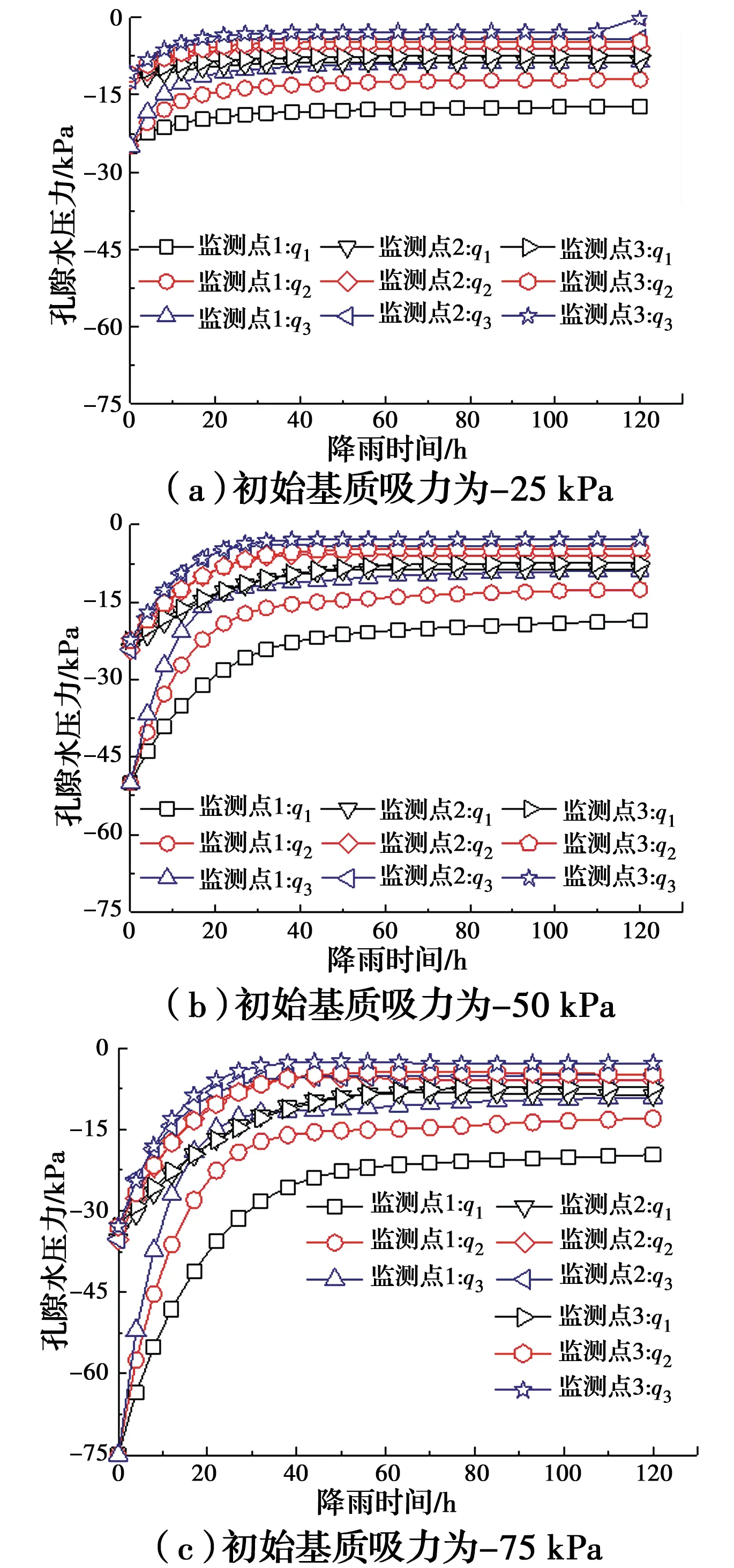
圖9 降雨時間過程中孔隙水壓力的分布Fig.9 Distribution of pore water pressure during rainfall

3.5 降雨條件下邊坡穩定性分析

由前述可知，在不同初始滲流場和降雨強度的影響下，降雨過程中邊坡的滲流特性和孔隙水壓力變化規律有所差異，因此，針對圖2所示邊坡，探討其邊坡穩定性的變化規律。當不考慮降雨時，對邊坡初始安全系數進行計算，最危險滑動面通過SLOPE/W程序自動搜索確定，采用有限單元應力法求解安全系數，以初始基質吸力為-25 kPa時為例，邊坡安全系數為1.623，最危險滑動面如圖10所示。由圖10可知，邊坡最危險滑動面同時位于壩體區和填埋嚴控區內，考慮到壩體潰決的可能性，為簡單起見，在降雨持續過程中，分析壩體區內(即監測截面3)的暫態飽和區厚度的變化規律對邊坡穩定性的影響。

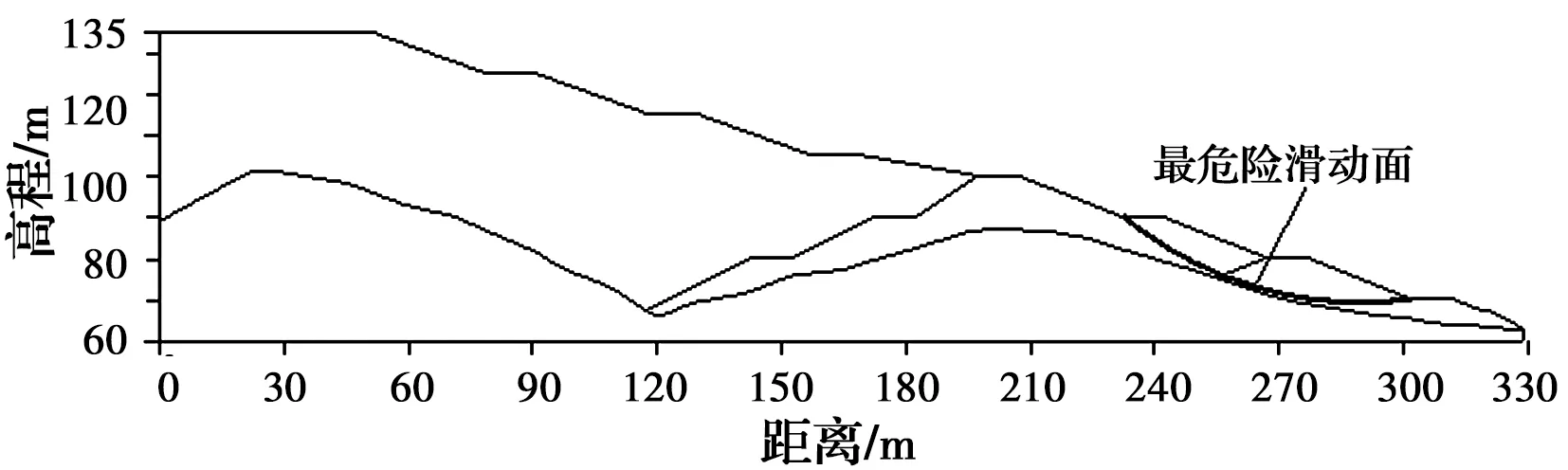
圖10 初始基質吸力為-25 kPa時的最危險滑動面Fig.10 The most dangerous sliding surface when the initial

降雨強度為q1～q3(1.5～3.5 mm/h)和不同初始滲流場時的邊坡安全系數變化如圖11所示。由圖11可知，暫態飽和區厚度對邊坡穩定性影響顯著，且邊坡初始基質吸力為-50、-75 kPa時，邊坡安全系數下降趨勢和暫態飽和區厚度增加趨勢均呈線性。此外，由圖11(a)可知，當降雨強度為q1時，邊坡沒有產生暫態飽和區，且初始基質吸力為-25 kPa時的安全系數下降速率最大；由圖11(b)可知，

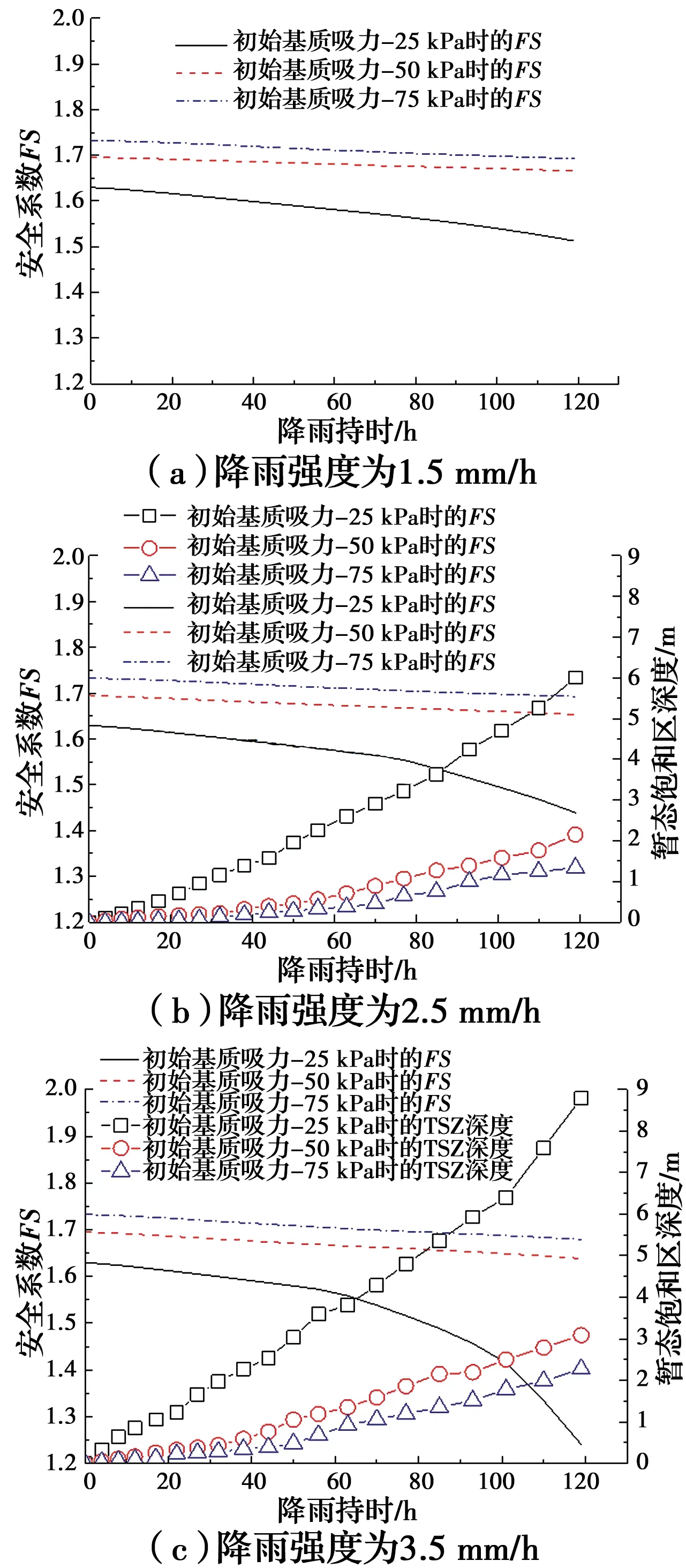
圖11 暫態飽和區厚度對邊坡安全系數的影響Fig.11 Influence of transient saturated zone thickness

降雨強度為q2時暫態飽和區的最大厚度分別為6.00、2.15、1.34 m，降雨結束后，邊坡安全系數分別為1.439、1.653、1.693；由圖11(c)可知，當降雨強度為q3時，初始基質吸力為-25 kPa的邊坡安全系數下降呈非線性趨勢，最小值為1.241，相應地，其暫態飽和區厚度增加也呈非線性趨勢，最大值為8.79 m。綜合圖11可知，在相同初始基質吸力條件下，暫態飽和區厚度為8.79 m時的安全系數與沒有暫態飽和區時的安全系數最大相差0.272，降幅約21.91%；在相同降雨強度下，暫態飽和區厚度為8.79 m時的安全系數與暫態飽和區厚度為2.27 m時的安全系數最大相差0.429，降幅約35.37%。

當初始基質吸力為-25 kPa時，邊坡初始安全系數為1.623，具備很好的安全儲備，而經歷120 h的強降雨后(q3=3.5 mm/h)，安全系數只有1.241，且結合監測點暫態飽和區形成時間規律可知，在降雨作用下，壩體區的地下水位大幅度上升，并已達到壩體區坡頂。目前，中國關于渣土場邊坡相關的設計規范還未成熟，若借鑒碾壓土石壩的設計標準：壩坡正常條件下的最小安全系數為1.25(簡化畢曉普法)，非正常運用條件Ⅰ時的最小安全系數為1.15(簡化畢曉普法)[26]。由此可知，在初始基質吸力更小或遭遇強度更大的降雨時，若沒有相應的工程措施，渣土場邊坡具有失穩風險。

4 討論

基于非飽和滲流原理和非飽和土強度理論建立數值模型，探討了初始滲流場和降雨強度對渣土場邊坡的降雨入滲特征及穩定性的影響，得到的結論為渣土場的長期運營及排水防滲工作提供了參考依據。

一般而言，在數值模擬研究中，常規邊坡多為單級邊坡，且構成物質單一，其在降雨作用下的滲流特征和穩定性分析已經比較明確。然而，渣土場邊坡基本為多級邊坡，其填筑過程分階段、分區域進行，這使得不同區域的巖土體力學參數存在差異，從而改變了渣土場邊坡的滲流特征，并顯著影響邊坡穩定性。具體體現為：需要綜合分析渣土場邊坡的整體穩定性和渣及其各自區域內單極邊坡的穩定性。從文獻[15]可知，在降雨作用下，渣土場邊坡下部的安全系數要小于其上部和中部的安全系數，為簡單起見，只計算了渣土場邊坡下部的安全系數，分析了渣土場邊坡發生“潰壩”的失穩隱患。綜合分析渣土場邊坡的多種失效模式將是下一步研究的工作重點。

另一方面，考慮初始滲流場影響的渣土場邊坡降雨入滲過程分析是從數值模擬的角度進行的，一定程度上可以為實際場地的相關分析提供理論支撐，在后續研究中應通過現場監測和模型試驗等手段對結果進行檢驗與修正。

5 結論

1)初始滲流場和降雨強度對渣土場邊坡的降雨入滲特征有顯著影響。初始基質吸力越大，Y方向流速的峰值越大，達到峰值的時間越長，且體積含水率上升速度越慢，達到飽和的時間越長。降雨強度越大，Y方向流速的峰值越大，達到峰值的時間越短，且體積含水率上升速度越快，達到飽和的時間越短。

2)渣土場邊坡暫態飽和區的滲流特征可描述為：壩體區坡面以下土體迅速飽和，暫態飽和區范圍由壩體區坡腳附近加速向上部土體擴散，并逐漸覆蓋整個壩體區，同時由壩體區向填埋嚴控區漫延。

3)初始基質吸力較大的邊坡孔隙水壓力上升速率快于初始基質吸力較低的邊坡。渣土區的孔隙水壓力上升速率最快，填埋嚴控區和壩體區的孔隙水壓力上升速率差別不大。降雨強度會顯著影響孔隙水壓力增長的快慢，而初始基質吸力影響較小。

4)初始滲流場對渣土場邊坡安全系數有顯著影響。邊坡安全系數與暫態飽和區厚度的關系為負相關。在初始基質吸力為-25 kPa時，經歷了120 h降雨后(3.5 mm/h)，渣土場邊坡安全系數下降明顯，具有一定的失穩風險，因此，在渣土場進行填筑的過程中，為確保壩坡長期穩定，應充分考慮區域氣象條件對渣土場運營期穩定性的影響，做好渣土場邊坡排水和防滲設施，防止發生壩體區潰壩。