基于思維導圖的“線性代數”形象化教學探究

[摘 要] 利用思維導圖把線性代數的抽象概念形象化。分別從行列式、向量組、零向量、秩及線性方程組出發，串聯出線性代數各個章節的知識點，加深同學對線性代數抽象概念的理解并認識前后各個知識點之間的關聯，培養學生解決復雜問題的綜合能力和高級思維。

[關鍵詞] 思維導圖;線性代數;形象化教學

[中圖分類號] G642.4? ?[文獻標識碼] A? ? [文章編號] 1674-9324（2021）01-0017-04? ?[收稿日期] 2020-03-10

線性代數是高等學校理、工、農、醫、經、管等學科大學生的一門重要基礎課程，也是后繼相關課程和將來科技工作的數學基礎。該課程包含了幾何概念與代數方法的聯系、嚴謹的邏輯推理、巧妙的歸納綜合等數學思想，對于培養學生的數學素養具有重要的作用。隨著計算機技術的飛速發展與廣泛應用，作為離散化和數值計算理論基礎的線性代數就顯得日益重要。

線性代數的學習對象都是大學低年級學生，他們在學習線性代數的過程中極易掉進中學數學慣性思維的陷阱，對很多概念和運算很容易搞錯、搞混淆。另外，抽象的概念、眾多的公式及煩瑣的運算使得線性代數課程成為學生學習中的“攔路虎”。所以，如何把線性代數的抽象概念形象化，是線性代數任課教師的首要任務[1]。

思維導圖是20世紀70年代英國學者提出的一種表達發散性思維的有效圖形思維工具，它既簡單，又很有效，是一種實用性很強的思維工具。思維導圖運用圖文并重的技巧，充分運用左右腦的機能，利用記憶、閱讀、思維的規律，協助人們在科學、邏輯與想象之間平衡發展，從而開啟人類大腦的無限潛能[2]。

線性代數知識的思維導圖是以某一個線性代數知識點為中心，將此知識點相關的定義、求法、性質、特點、關系、判定及應用等內容以圖的形式展現，有效激發學生腦神經，促進學生記憶、理解、關聯相關知識，達到對線性代數知識系統的整體把握[3]。

一、用行列式串聯線性代數各個章節內容

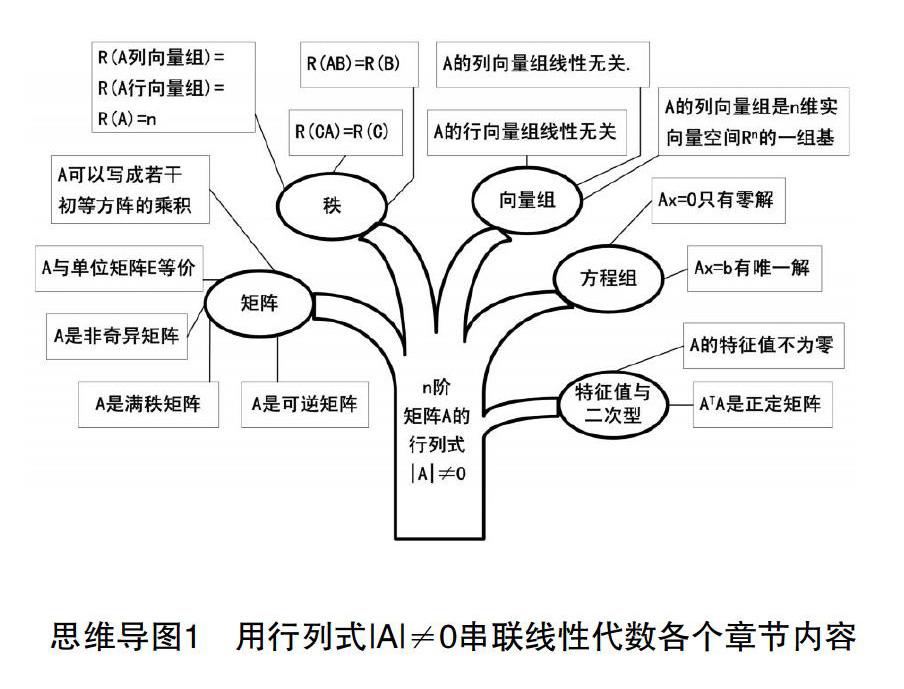
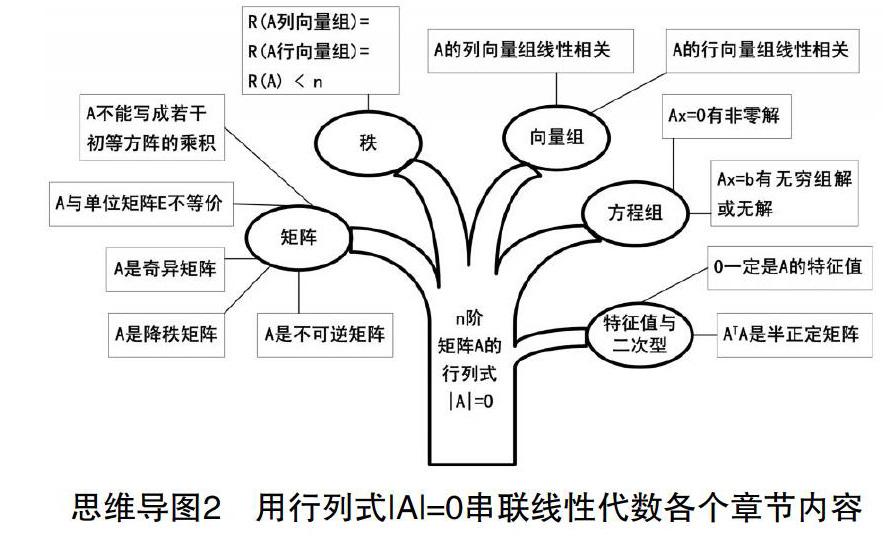
行列式是大多線性教材的第一章內容，但它貫穿在線性代數的各個章節中，把線性代數各個章節內容之間的相互關系搞清楚是學好線性代數的關鍵。思維導圖1和思維導圖2分別從n階行列式|A|不等于零和等于零兩種情況出發，串聯出線性代數各個章節所相關的知識點[4]。

二、零向量在線性代數章節中充當重要角色

零向量是一個非常特殊的向量，在向量組的線性相關性的定義、矩陣秩的計算、線性方程組、向量空間及特征值特征向量等知識中起到非常重要的作用。思維導圖3分別從零向量的作用、特點、唯一性和“不能作為的角色”出發，闡述了零向量在線性代數知識體系中的重要性[4]。

三、用秩的概念來闡述線性代數各個章節內容

秩是線性代數知識體系中一個非常重要的概念，矩陣有秩，向量組有秩，二次型也有秩，它們之間既有區別又有聯系，初學線性代數的同學往往對秩的概念理解不深刻，出現各種錯誤。思維導圖4給出了矩陣秩、向量組秩及二次型秩的定義和求法;給出了矩陣秩和向量組秩之間的關系;給出了矩陣秩的含義;給出了利用秩判定線性方程組解的定理;給出了向量空間與秩的關系[5]。

四、用向量組的線性相關性串聯線性代數各個章節內容

向量組的線性相關性是線性代數課程中的重點和難點，當很多同學學到這一概念時，就開始對線性代數課程產生了畏懼心理。在線性代數知識的學習中，不能完全獨立地學習某一個知識點，而是應該把各個章節知識點聯系起來學習，思維導圖5從三個三維線性無關的列向量出發，串聯出各個章節所相關的知識點;思維導圖6從三個三維線性相關的列向量出發，串聯出各個章節所相關的知識點[5]。

五、用齊次線性方程組解的情況串聯線性代數各個章節內容

線性方程組是線性代數的核心，它是整個線性代數知識體系的主線。思維導圖7從只有零解的齊次線性方程組出發，串聯出線性代數各個章節所相關的知識點;思維導圖8從有非零解的齊次線性方程組出發，串聯出線性代數各個章節所相關的知識點[6]。

六、思維導圖在教學中的應用

在2020年的疫情防控期間，全國各個高校都大力開展了網絡教學，使得教師的教和學生的學在時間和空間上都發生了很大變化。在這種特殊情況下，利用思維導圖開展教學，收到了非常好的教學效果。

首先，線性代數很多概念抽象難懂，教師把思維導圖應用到線性代數課程的教學中，很好地實現了線性代數的形象化教學，增加了學生對概念的深入理解，搞清了各個概念間的邏輯關系，并有助于同學記憶相關知識，大大提高了教學質量，得到了同學的好評。

其次，線性代數課程有一個非常大的特點就是各個章節內容相互關聯、相互滲透，教師把思維導圖運用到線性代數各個章節的教學中，使學生掌握了各個章節知識點之間的關聯，并且增強了知識點的趣味性，激發了學生的自主學習意識，大大加強了師生之間的溝通，提高了學生團結協作的學習能力。

最后，教師還應該引導和鼓勵學生親自動手制作線性代數各知識點的思維導圖，進一步培養學生解決復雜問題的綜合能力和高級思維。

參考文獻

[1]楊威，高淑萍，陳懷琛，等.新工科背景下線性代數教學改革與探索[J].高教學刊，2020（5）：8-12.

[2]陳云輝，謝百治，趙麗.思維導圖與學生創新思維能力培養[J].中國醫學教育技術，2006（2）：10-12.

[3]楊鑫剛.思維導圖在線性代數課堂教學中的應用[J].教育教學論壇，2018（14）：190-191.

[4]楊威.線性代數輔導講義[M].北京：電子工業出版社，2011.

[5]楊威.線性代數名師筆記[M].西安：西安電子科技大學出版社，2014.

[6]陳懷琛，高淑萍，楊威.工程線性代數[M].北京：電子工業出版社，2007.