面向多星區域觀測調度的改進型自適應遺傳算法

樊育，劉瑩瑩，周軍

西北工業大學 航天學院，西安 710072

地球觀測衛星(Earth observation satellite, EOS)可以實現對指定點目標或區域目標的觀測成像。但是，如果衛星不具有側擺能力，那么衛星僅能對其星下點軌跡上視場角范圍內的目標實現觀測；而實際任務目標中的大部分區域都是沒有在指定衛星星下點軌跡上及其視場角范圍內的。因此在衛星不具有側擺能力的情況下，對指定區域目標的覆蓋效率是很低的。為了解決這個問題，可將星載相機在垂直于衛星星下點軌跡的方向上進行擺動，以此實現對未在星下點軌跡上及其視場角范圍內的目標進行觀測，大大提高衛星的對地覆蓋效率。另外，隨著微小衛星的發展，大大降低了衛星的制作成本，使得越來越多的衛星組成衛星星座[1-2]去完成對指定區域目標的觀測成為各個國家和企業的研究重點。

當今資源充分利用的環境下，如何利用一定的衛星資源實現對目標區域最大程度的覆蓋[3]，已經是研究對地觀測衛星的熱點問題，引起眾多學者的關注。伍國華等[4-5]提出了動態聚類調度算法(dynamic clustering scheduling algorithm, DCSA)來解決多星多軌道圈次的觀測調度問題，并使用模擬退火算法搜索全局最優解；李仕學等[6]面向月表大區域成像任務需求，提出了拼接成像側擺角優化方法，并提出基于sigmoid函數的自適應遺傳算法(sigmoid adaptive genetic algorithm, SAGA)對其進行求解；Wang等[7]為了提高計算效率，考慮了當前任務與歷史任務的相似性，提出具有檢索、匹配和修正的相似性學習法，并結合遺傳算法對實際觀測任務進行求解，大大加快了任務的求解速度； Fei等[8]考慮衛星傳感器的實際側擺能力，結合貪婪算法的思想提出一種動態劃分目標區域的算法；Xu 等[9]針對多衛星區域調度問題，提出一種3階段解決框架，即離散、分解和調度階段，在最后一階段利用遺傳算法進行求解；Zhu等[10]綜合考慮地球觀測衛星調度中的成像與數據傳輸問題，提出了一種兩階段遺傳模擬退火算法去解決調度問題；Wu等[11]針對調度任務中的重要緊急任務調度處理，提出一種結合局部搜索的混合蟻群算法對調度問題進行優化；劉華俊等[12]針對現有覆蓋算法低效耗時的技術瓶頸，提出了一種針對成像衛星區域覆蓋的自適應規劃方法，包括自適應的網格劃分、平衡成像精度和覆蓋效率的最大可視覆蓋計算以及窗口優化的衛星區域覆蓋策略。

在以上研究中還存在以下不足：1)文獻[4-5]只研究了點目標任務的聚類調度問題，針對區域目標的調度問題還未研究；2)文獻[6]只研究了單星成像問題，并未對多星成像問題進行研究；3)文獻[12]提出的優化方法只找到一個局部最優解，并不能保證其全局最優性；4)都是通過STK(Satellite tool kit)獲得時間窗口，沒有通過軌道六要素自主計算星下點軌跡，從而獲得對目標觀測的時間窗口，使得程序算法缺乏靈活性；5)都是僅僅以衛星對地觀測的覆蓋率作為唯一的收益指標，均未考慮對目標區域總覆蓋時間這一指標；而這一指標直接反映了衛星在規定時間內對指定目標的觀測時間長短，是一個重要的覆蓋指標。

基于以上情況，本文根據衛星的軌道六要素計算出星下點軌跡，并采用網格點法自主劃分區域目標，在指定的最大側擺角范圍內計算出每顆衛星每次過境的時間窗口，得出每顆衛星在每次過境時段內的側擺角集合。最后將問題轉化為多個時間窗口和多個側擺角集合的動態組合調度優化問題，為了更高效地實現目標收益的最大化，提出了結合平均Hamming距離、神經元激活函數sigmoid和高斯函數的改進型自適應遺傳算法(Hamming distance sigmoid Gauss function adaptive genetic algorithm, HSGAGA)對此動態組合調度優化問題進行求解，并通過算例與其他常用的優化算法,包括標準遺傳算法(genetic algorithm，GA)、改進型遺傳算法(improved genetic algorithm,IGA)、標準模擬退火算法(simulated annealing algorithm,SA)、改進型模擬退火算法(improved simulated annealing algorithm，ISA)進行對比，驗證了本文所提出的HSGAGA算法的優良性能。

1 衛星對目標的側擺角度計算

1.1 星載遙感器的覆蓋能力

在衛星具有側擺能力的情況下，衛星在軌道上對地的觀測角指的是衛星在垂直于星下點軌跡的方向上，視場角與側擺角的結合。如圖1所示。

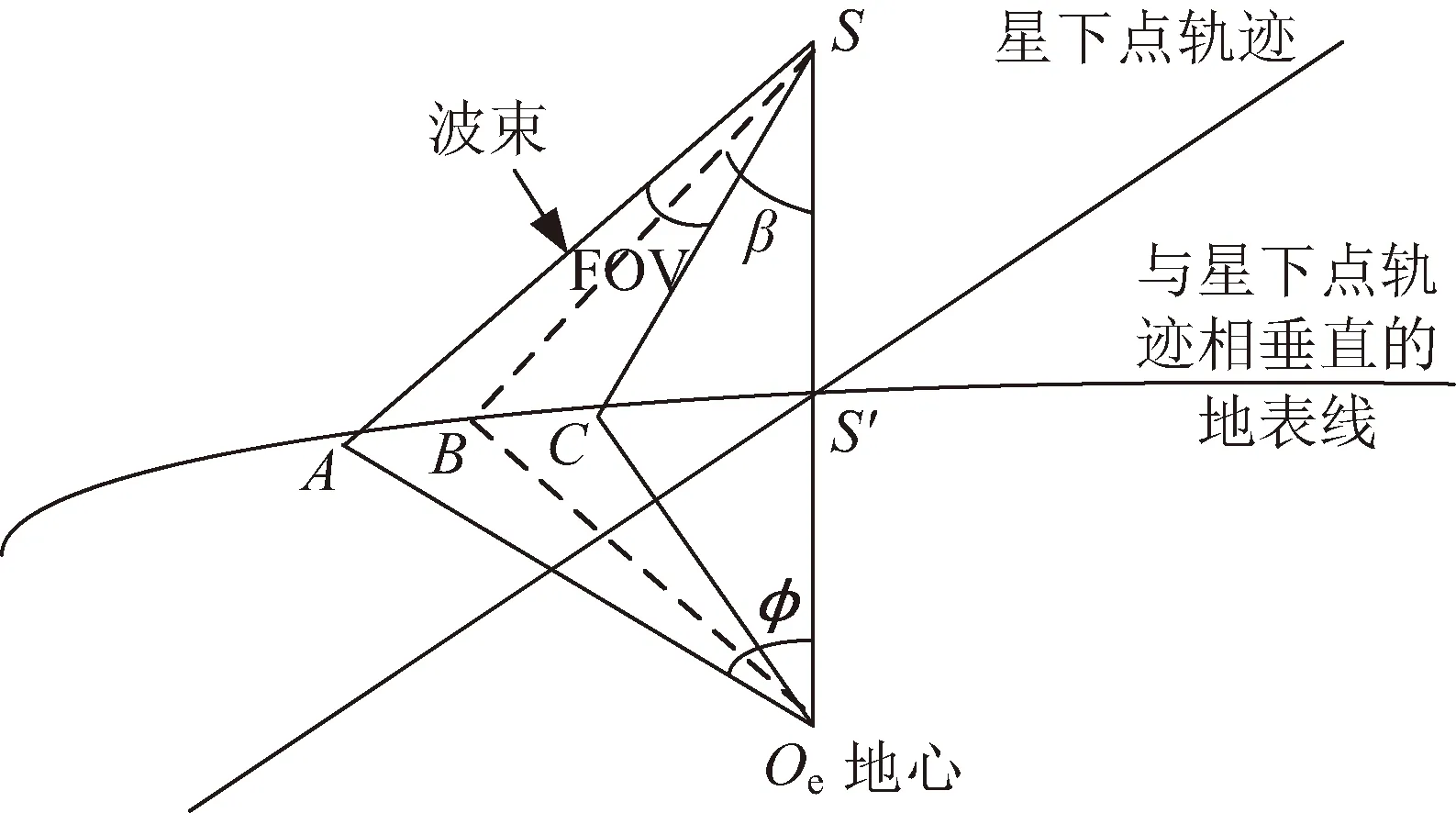
圖1 衛星對地覆蓋示意Fig.1 Illustration ofsatellite coverage

若衛星某時刻t的瞬時軌道高度為h，相應星下點為S′，星載遙感器的側擺角度為β，視場角為FOV(field of view)，則衛星對地觀測角為β+FOV/2。假設地球是一半徑為Re的均勻圓球體，h為衛星軌道高度，衛星距地心距離SOe=h+Re，由幾何關系，此時弧段AS′對應的地心覆蓋角φ為：

(β+FOV/2)

同時，由地心覆蓋角可得覆蓋幅寬為：

AS′=φ·Re

當然，對于不同高度的軌道衛星，觀測角β+FOV/2也有其相應的約束范圍，如圖2所示。

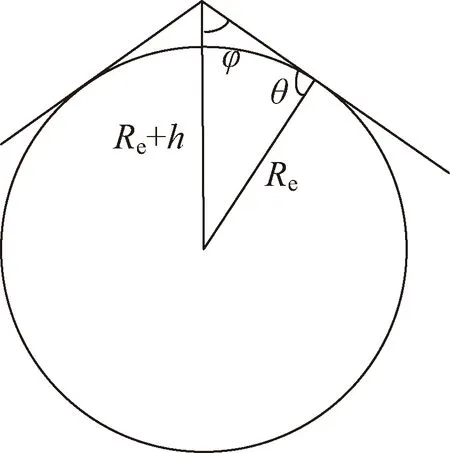
圖2 衛星對地觀測范圍示意Fig.2 Illustration of satellite observation range

最大觀測角即就是觀測邊界與地球相切，即θ=90°，根據幾何關系，軌道高度為h的衛星對地最大觀測角為：

即有觀測角約束：

β+FOV/2≤φ

而且，對于不同高度、不同相機幅寬的軌道衛星，對地觀測的視場角FOV也不同，如圖3所示，其中l為相機半幅寬。

根據幾何關系，軌道高度為h，相機幅寬為2l的衛星對地觀測的視場角大小為：

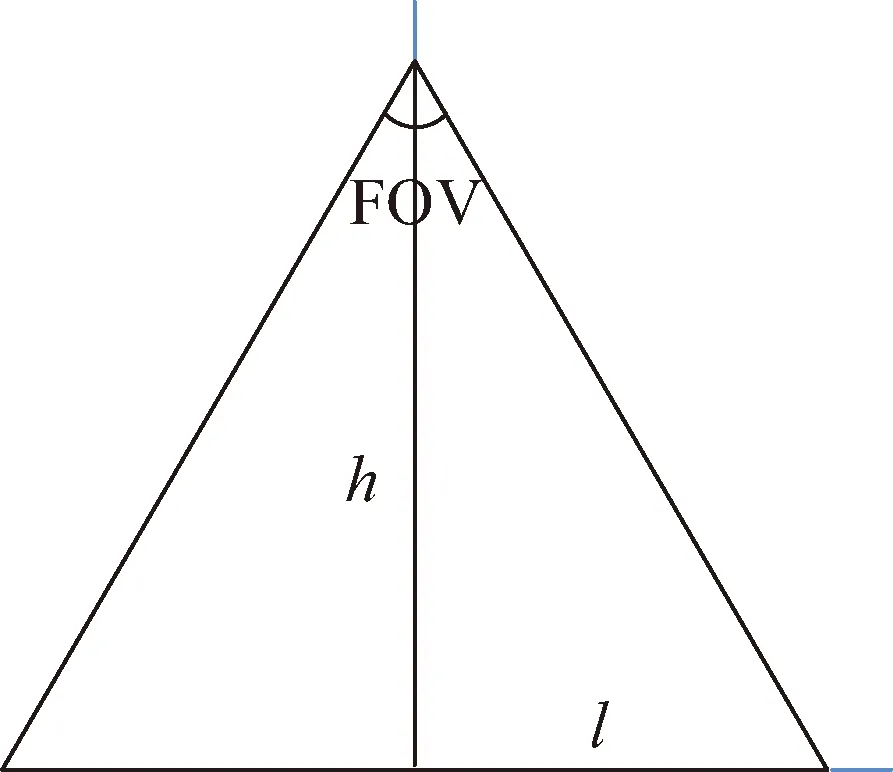
圖3 衛星相機半幅寬l與視場角FOVFig.3 Satellite camera width l and field of view FOV

1.2 側擺角度的計算

對于衛星對區域目標的側擺角度計算，可采用經典的網格點法將區域目標轉化為點目標集合，進而將問題轉化為衛星對區域點集合中各個點的側擺角度計算。此時，采用點的包含性檢驗來判斷是否可見，同時計算出側擺角集合。

如圖1所示，若目標點位于B(λ,φ)，則過B點作垂直于衛星星下點軌跡的垂線，并與其交與S′(λx,φx)。根據幾何關系，采用基于球面三角學的大圓距離求解算法，得目標點B與衛星星下點S′的弧長BS′為：

BS′=arccos[sinλsinλx+

cosλcosλxcos(φx-φ)]·Re

則地心覆蓋角∠BOeS為：

∠BOeS=BS′/Re

最后，在三角形BOeS中，根據幾何關系，求得處于S處的衛星對目標點B的側擺角度β為：

2 多星觀測調度模型

2.1 問題特點及約束分析

對于本文所研究的多星觀測調度問題，具有如下的特點及約束。

1)衛星調度方式：所有衛星僅在垂直于星下點軌跡的方向上具有側擺能力。

2)衛星機動能力約束：限制衛星在同一過境時段內，只能以單一的側擺角進行過境，在不同過境時段內，可以以不同的側擺角進行過境。

3)光照條件約束：為了獲得衛星對指定目標更好的的觀測信息，必須要保證衛星對指定目標觀測時的太陽高度角，即任一顆衛星對區域目標內的任意一個子目標進行觀測時，太陽高度角[13]都必須大于所要求的保證良好光照條件的臨界值。

2.2 調度模型中的參數含義及表示

1)Sat={S1,S2,…,SNS}表示衛星資源集合，即在調度任務中共有NS顆對地觀測衛星資源可執行目標區域的觀測任務。

2)O={oi|i=1,2,…,Ni}表示衛星對目標區域進行過境的軌道圈次資源，Ni表示多顆衛星的總的過境次數。

3)T={ti|i=1,2,…,N}是待觀測的目標集合，N表示總任務數量。

4)Twrj={twrj1,twrj2,…,twrjNrj}表示在考慮天氣條件的情況下，衛星r對目標j的Nrj個可見時間窗口，其可寫為twrjm=[Strjm,Etrjm]。其中Strjm、Etrjm分別表示衛星r對候選任務j的第m個可見時間窗口的開始時間和結束時間。

(5)βr,i={βr,i,1,βr,i,2,…,βr,i,Ng}表示衛星r在第i次過境下可供選擇的Ng個側擺角集合。

(6)v={v1,v2,…,vi,…,vr}表示衛星r上的傳感器要對準待觀測目標時的側擺速率。

(7)a={a1,a2,…,ai,…,ar}表示衛星r在對某個目標觀測之前的傳感器開機時間。

(8)wr={wr,1,wr,2,…,wr,oi,…,wr,N}表示衛星r在過境圈次oi上對地觀測活動消耗星上存儲資源的速率。

(9)Wr={Wr,1,Wr,2,…,Wr,oi,…,Wr,N}表示衛星r在過境圈次oi上允許消耗的最大存儲資源。

(10)Xr,i,j={Xr,i,j,1,Xr,i,j,2,…,Xr,i,j,N}表示衛星r在第i次過境第j次側擺情況下對各個目標點的可見性集合。若Xr,i,j,k=1，則表示衛星r在第i次過境第j次側擺情況下對目標點k可見；反之，若Xr,i,j,k=0，則表示對目標點k不可見。

(11)tmr,i,j={tmr,i,j,1,tmr,i,j,2,…,tmr,i,j,N}表示衛星r在第i次過境第j次側擺情況下對各個目標點的觀測時刻集合。若tmr,i,j,k=t(t≠0)，則表示衛星r在第i次過境第j次側擺情況下對目標點k的觀測時刻為t；反之，若tmr,i,j,k=0則表示對目標點k不可見。

(12)tcr,i={tcr,i,1,tcr,i,2,…,tcr,i,Ng}表示衛星r在第i次過境且采用各個側擺角的情況下對目標區域的覆蓋持續時間。若tcr,i,j=t(t≠0)，則表示衛星r在第i次過境第j次側擺情況下對目標區域的持續覆蓋時間為t；反之，若tcr,i,j=0則表示對目標區域不可觀測。

2.3 調度模型的建立

在指定時間段內，衛星對地觀測的覆蓋指標主要有兩個：一是對目標區域的覆蓋率；二是對目標區域總的覆蓋時間。為了綜合考慮這兩種覆蓋指標，此多星觀測調度問題的目標收益取為：

式中：{x1,x2,…,xN}為決策向量集，xi表示多顆衛星第i次過境時選擇第xi個側擺角；wk為各覆蓋指標的權值；fk{x1,x2,…,xN}為在決策向量集{x1,x2,…,xN}下的第k個覆蓋指標的值，f1、f2分別表示覆蓋率和總的覆蓋時間。

調度過程中需要滿足復雜的約束條件，如下所示。

1)側擺角約束：考慮機動能力，任意側擺角都必須不大于最大側擺角，否則將不能側擺成功。

2)側擺時間約束：任意一顆衛星在對指定目標相鄰兩次過境觀測過程中，所間隔的時間必須不小于衛星星載設備所需機動調整的時間，即：

3)存儲容量約束：在第oi次過境觀測中，衛星所獲得的觀測信息容量必須不大于衛星單軌運行所允許的最大存儲容量，即：

3 改進型自適應遺傳算法

3.1 算法實現流程

遺傳算法(GA)是由Holland[14]于20世紀70年代提出的一種基于自然選擇法則的搜索尋優算法。但標準遺傳算法在交叉操作和變異操作中的交叉率和變異率為固定值，對于耦合性較高的復雜優化問題，不利于種群的進化而易于陷入局部最優。

為了改進這一缺陷，Srinivas、任子武等[15-16]提出了自適應遺傳算法，但在進化初期或后期，都存在易陷入局部最優的問題。

為了更快更高效地搜索到全局最優解，實現目標收益的最大化，本文提出了結合平均Hamming距離、神經元激活函數sigmoid和高斯函數的改進型自適應遺傳算HSGAGA對動態組合調度優化問題進行求解，其算法流程如圖4所示，其中R表示染色體長度。

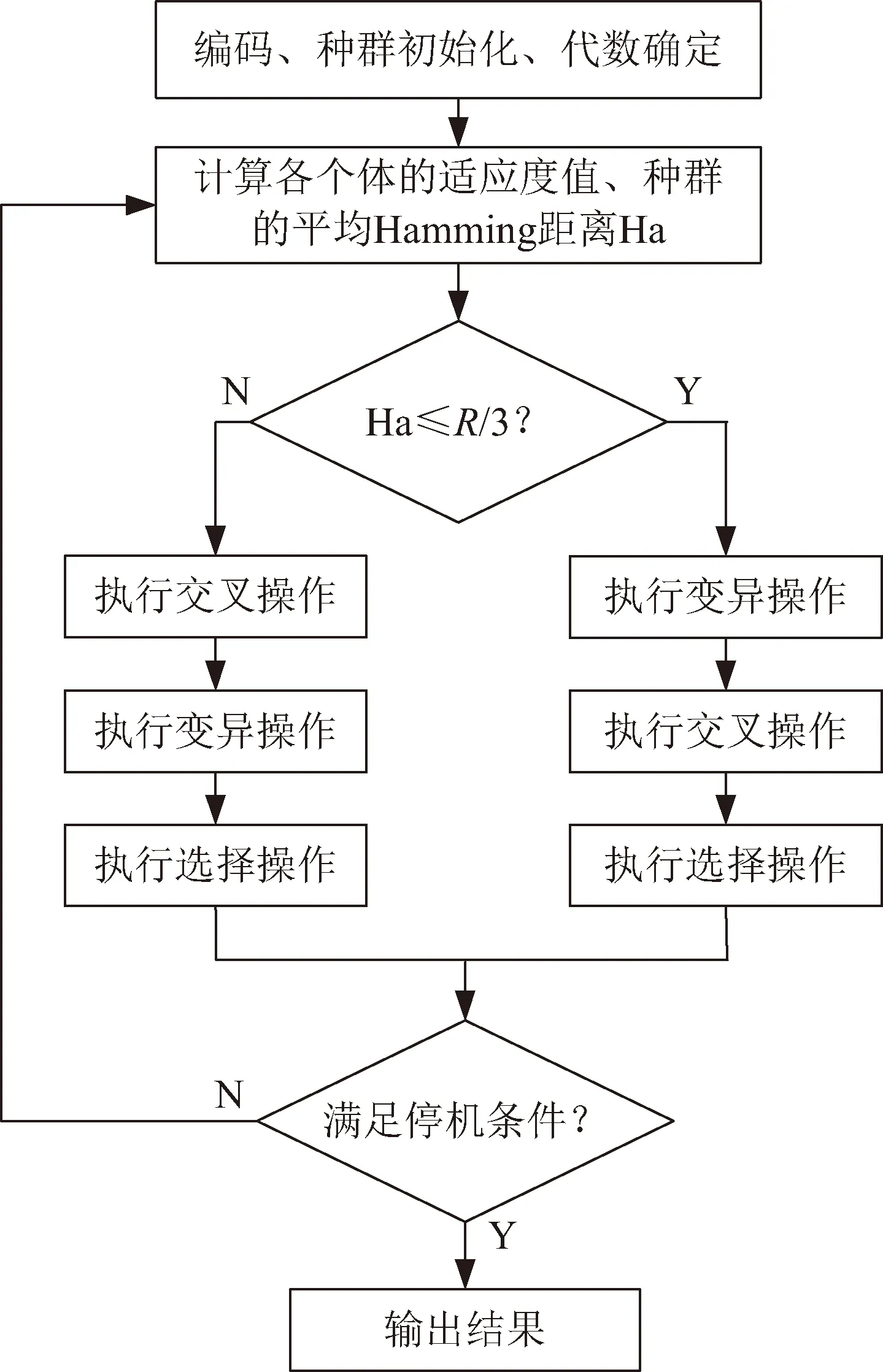
圖4 改進型自適應遺傳算法HSGAGA的流程Fig.4 Flowchart of improved adaptive genetic algorithm HSGAGA

3.2 算法典型步驟

(1)編碼

采用k進制編碼，直接將決策向量集x={x1,x2,…,xN}作為染色體，x中的元素xi作為基因。k編碼類似于十進制編碼，唯一不同的是十進制編碼中基因的取值為0～9之間的整數，而k編碼中基因的取值為1～k之間的整數。

(2)種群初始化

使用蒙特卡洛方法逐步生成初始種群中的個體，并且通過比較兩個k進制編碼的染色體對應基因不同的個數作為Hamming距離，以此來控制初始種群的個體差異，改善初始種群的活力，以擴大種群的多樣性。具體方法如下：若新產生的個體與前面已產生的某一個體的Hamming距離小于染色體長度的三分之一，則摒棄此新個體，重新產生新的個體，直到種群初始化結束。

(3)交叉、變異操作的順序確定

基本的遺傳算法不論種群適應度如何變化，都是先進行交叉操作，后進行變異操作。這在種群的進化中，易于導致種群早熟而陷入局部最優解。如在種群進化后期，種群個體差異很小，此時倘若先進行交叉操作，則對優良個體的產生基本沒有作用，縮小了搜索空間，使得種群陷入局部最優。

因此提出一種根據當代種群平均Hamming距離對交叉與變異操作的順序進行確定的方法：

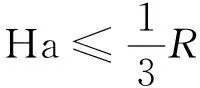
(1)

式中：Ha為當代種群的平均Hamming距離。若式(1)成立，說明此時種群多樣性較小，應先進行變異操作，后進行交叉操作；反之，應先進行交叉操作，后進行變異操作。

(4)改進型的交叉操作、變異操作

本文中的交叉操作選擇以“門當戶對”原則且結合混沌序列[17]的多點交叉，利用混沌序列產生待交換位置串，進而實行多點交叉。變異操作選擇結合混沌序列的多點變異。

交叉操作和變異操作中的交叉率和變異率是決定算法收斂速度、穩定程度的關鍵參數。交叉率是種群進化的基礎，交叉率越大，種群越豐富，算法搜索空間越大，但優良個體被破壞的可能性也越大；交叉率過小，不易產生新個體，而最后陷于早熟現象。變異率則是產生全局最優解的關鍵一步，變異率過小，不易產生新個體，而最后陷于局部最優；變異率過大，又會使遺傳算法趨近于隨機搜索算法，大大增加了運算開銷。

本文基于sigmoid函數[18]和高斯基函數[19]對交叉率和變異率進行改進，設計出一種自適應非線性調整交叉率和變異率的調節公式，如下所示：

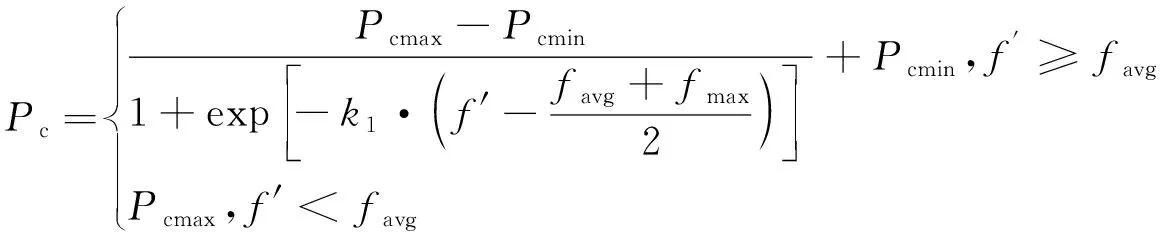
(2)

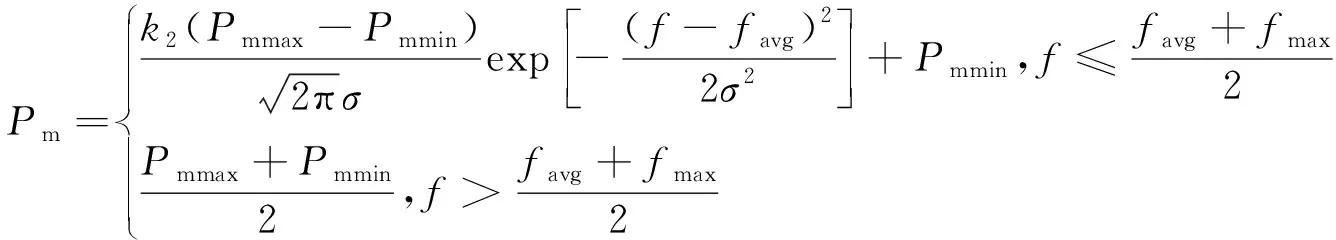
(3)

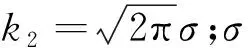
根據式(2)和式(3)繪制本文HSGAGA算法中自適應交叉率和變異率的調整曲線，如圖5和圖6所示。

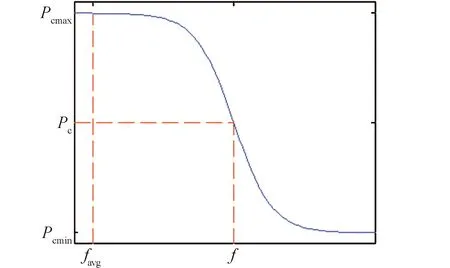
圖5 自適應交叉率調整曲線Fig.5 Curve of adaptive crossover rate

圖6 自適應變異率調整曲線Fig.6 Curve of adaptive mutation rate

由圖5和圖6可以看出：首先，在種群進化初期，由蒙特卡洛方法和Hamming距離生成的種群多樣性可以在較大的交叉率下充分發揮作用，產生初始的優良個體；并且，較小的變異率可以阻止對初始優良個體的破壞，增加了算法的收斂速度。其次，在種群個體適應度與種群平均適應度favg相近時，為了防止種群產生“早熟”現象而陷入局部最優，給予了較大的交叉率Pc和變異率Pm，增加種群的多樣性，避免了算法停滯不前。最后，當種群個體適應度接近種群最大適應度fmax時，說明種群的多樣性很低，此時通過交叉操作已經不能產生更優的個體，應給予較小的交叉率Pc，而為了增加種群的多樣性，防止種群“早熟”而陷入局部最優解，應適當地增加變異率Pm。

(5)選擇操作

結合雙精英保留策略和錦標賽選擇策略[20]對經過交叉和變異之后的種群進行選擇操作，構成新的種群。

雙精英保留策略：為了防止遺傳算法在運行過程中，由于交叉和變異等遺傳操作破壞了當前種群中的最優個體，大大影響遺傳算法的收斂速度，這里提出一種雙精英保留策略，主要思想是，若下一代種群中的最優個體適應度小于當代種群中的最優個體適應度，則用當代種群中最優的兩個個體替換掉下一代種群中最差的兩個個體，以保證種群的收斂能力，增大種群的收斂速度。

錦標賽選擇策略：模擬錦標賽競爭的方式，通過隨機選擇多個個體，并在多個個體中通過擇優錄取的方式實現選擇操作。

(6)停機條件

采用雙重停機條件。傳統的遺傳算法通常采用單一的g停機條件，即若進化代數達到預先給定的總的進化代數g，則結束算法運行。但若初始種群較優且參數選取非常理想，使得遺傳算法很快能夠搜索到最優解，倘若此時仍采取單一的g停機條件，便會額外增加算法的運行時間。

因此，本文算法在執行過程中，采用雙重停機條件：進化代數達到總的進化代數g；連續N次進化的最優結果不變。在遺傳進化過程中，滿足上述兩個條件中的任何一個，都結束算法的運行，大大提高了算法的收斂速度，減少了額外的計算時間。

4 仿真實驗

4.1 衛星及目標區域參數設置

為了驗證本文多星調度模型以及改進型自適應遺傳算法HSGAGA的性能，進行仿真實驗的衛星及目標區域參數設置如下。

(1)衛星軌道參數

由于對地觀測衛星要求較好的光照條件以及一定的回歸特性和穩定性[13]，因此本文使用的3顆衛星軌道均是作者設計的太陽同步回歸凍結軌道，降交點地方時均為早上10:30:00，具體軌道參數如表1所示。

a,e,i,Ω,ω,f指軌道六要素，分別為軌道半長軸、偏心率、傾角、升交點赤經、近地點幅角、真近點角。衛星上傳感器的相機幅寬均為2l=20 km；各衛星機動能力所限制的最大側擺角為βmax=±30°；各衛星上傳感器的側擺速率為v=1(°)/min ；各衛星對地觀測消耗星上存儲資源的速率為w=1.5 Mbyte/s；各衛星單軌運行所允許的最大存儲容量為W=90 Mbyte；能夠清晰地觀測到目標所要求的太陽高度角不小于10°；調度模型中目標收益的權值分別取為ω1=0.9，ω2=0.1。

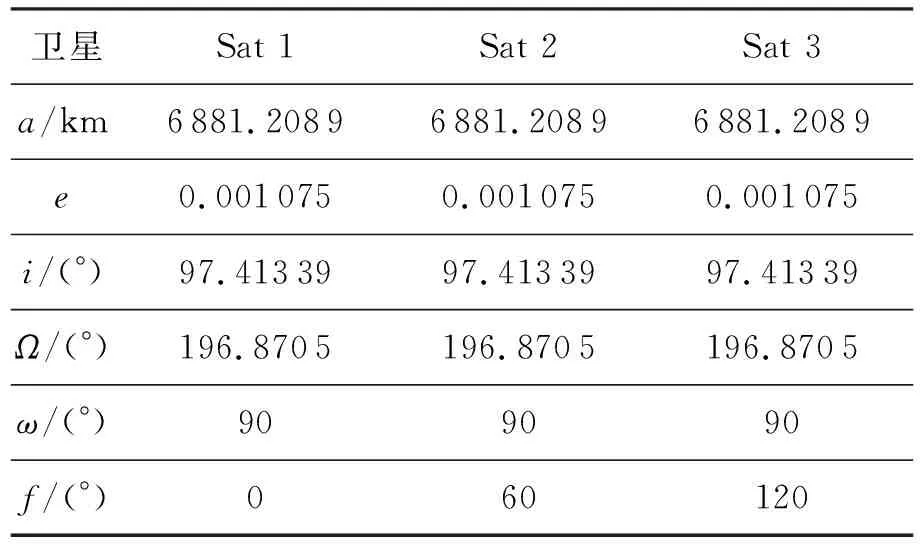
表1 衛星參數

(2)目標區域參數

目標區域選擇包括西安市在內的一個矩形區域，其4個頂點的經緯度坐標分別為(100°,30°)(110°,30°)(110°,40°)(100°,40°)。通過網格化方法，對此區域進行網格化，一共劃分為13×13=169個網格點；且觀測開始時間為2018-05-01 12:00:00，結束時間為2018-05-06 12:00:00。

4.2 算法參數設置及計算結果

為了驗證本文改進型自適應遺傳算法HSGAGA的性能，將其與標準遺傳算法(GA)、結合改良圈、混沌序列的改進型遺傳算法(IGA)、文獻[6]中所提出的基于sigmoid激活函數的自適應遺傳算法(SAGA)、模擬退火算法(SA)、結合蒙特卡洛方法的改進型模擬退火算法(ISA)進行對比，分別對此次調度問題進行求解。

算法采用Matlab r2012a實現，計算機的CPU為Pentium E5800，內存為3.00 Gbyte。其中各算法的參數設置如下：

SA算法：初始溫度為T0=1，降溫系數為α=0.999，終止溫度為e=0.130，退火最大次數為T=40000。

ISA算法：初始溫度為T0=1，降溫系數為α=0.999，終止溫度為e=0.130，退火最大次數為T=40 000。

GA算法：種群大小為w=30，最大進化代數為g=1 000，交叉率為Pc=0.7，變異率為Pm=0.1。

IGA算法：種群大小為w=30，最大進化代數為g=1 000，交叉率為Pc=0.7，變異率為Pm=0.1。

SAGA算法：種群大小為w=30，最大進化代數為g=1000，最大交叉率為Pcmax=0.8，最小交叉率為Pcmin=0.5，最大變異率為Pcmin=0.2，最小變異率為Pcmin=0.05。

HSGAGA算法：種群大小為w=30，最大進化代數為g=1 000，最大交叉率為Pcmax=0.8，最小交叉率為Pcmin=0.5，最大變異率為Pcmin=0.2，最小變異率為Pcmin=0.05，停機代數為150。

分別使用以上6種算法對本文的多星觀測調度問題進行求解。其中，SA算法、ISA算法獲得退火次數與每次退火后個體適應度值的關系如圖7所示；HSGAGA算法、GA算法、IGA算法、SAGA算法獲得進化代數與每代種群最大適應度值的關系如圖8所示。

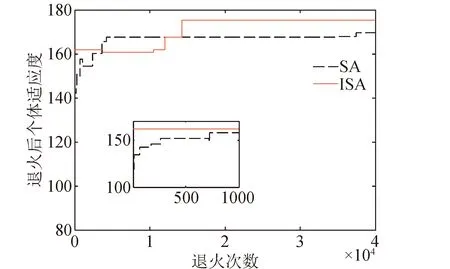
圖7 SA、ISA算法的性能比較Fig.7 Performance of SA and ISA

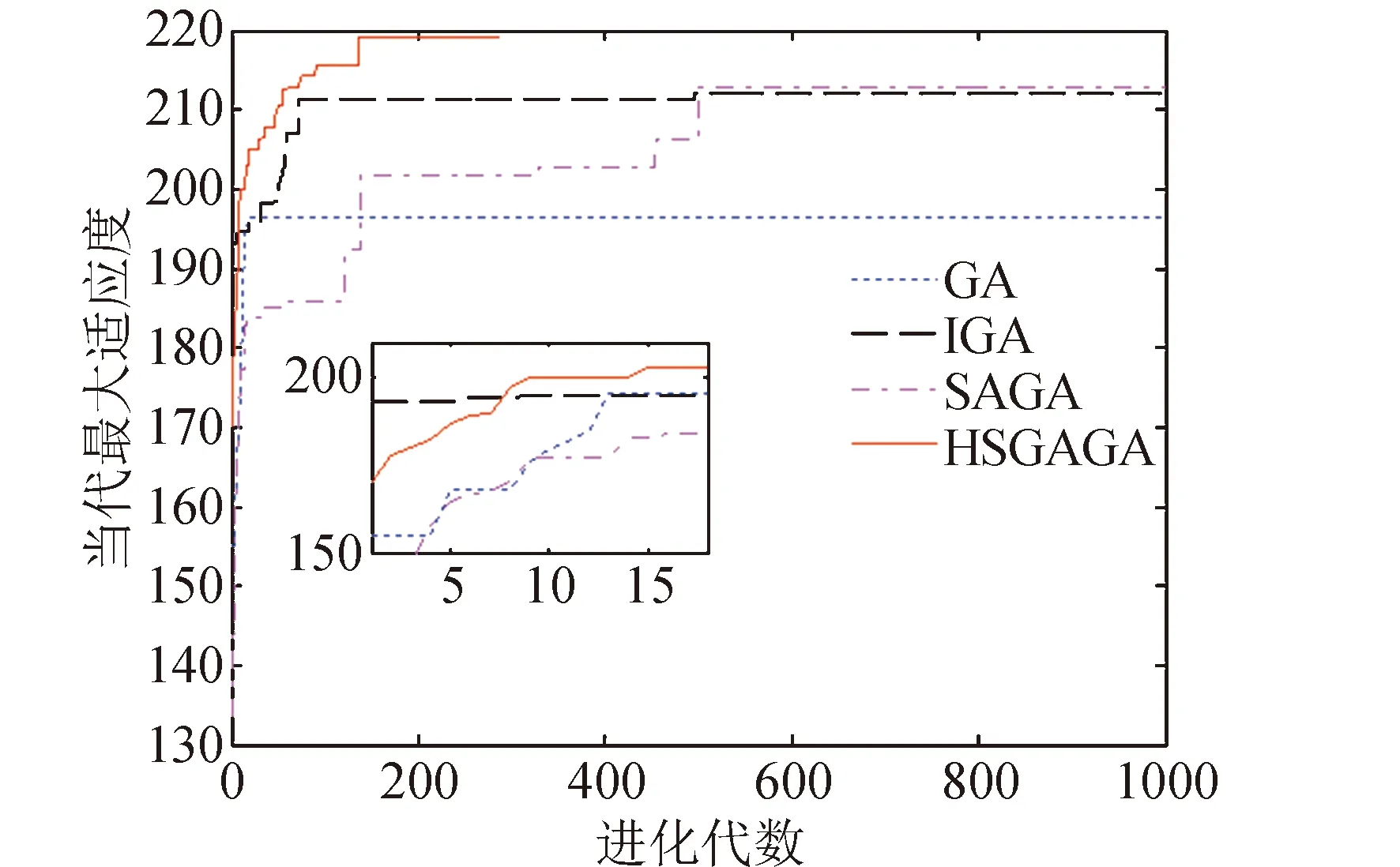
圖8 GA、IGA、HSGAGA算法的性能比較Fig.8 Performance of GA, IGA and HSGAGA

在HSGAGA算法下，這3顆衛星開始觀測到區域目標的時間、側擺角和覆蓋持續時間如表2所示。

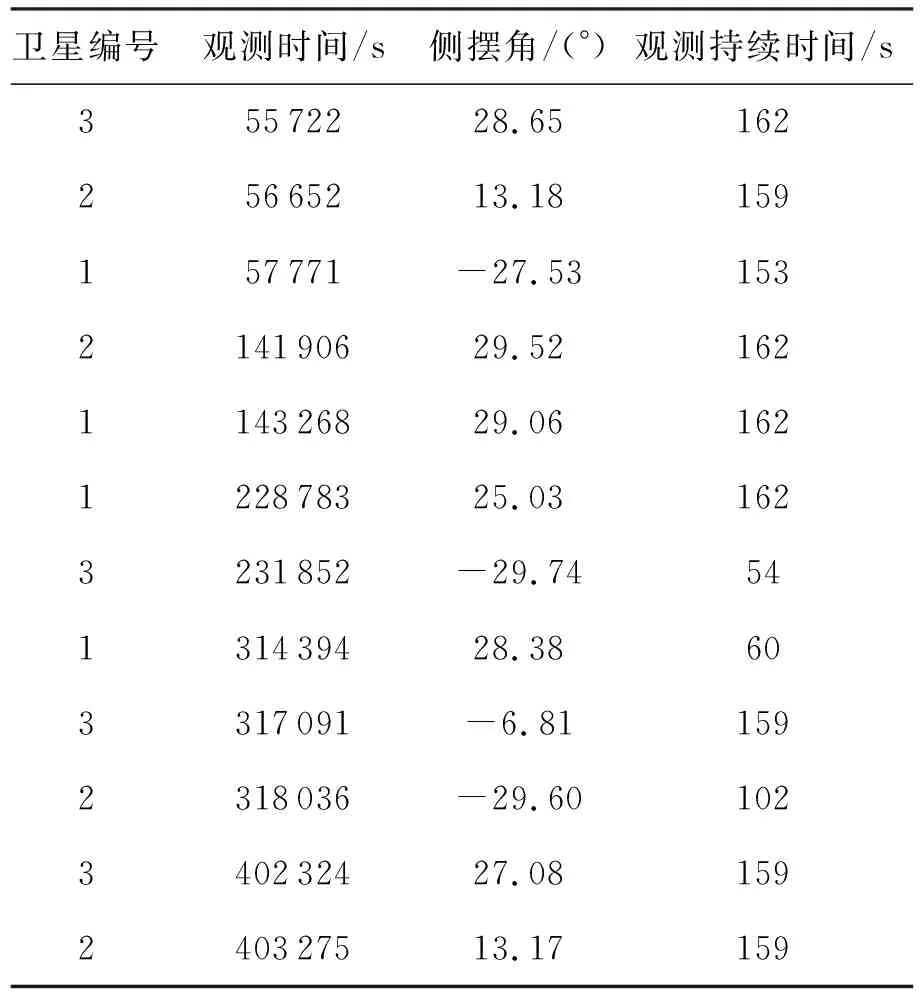
表2 HSGAGA算法下各衛星的觀測結果

使用這6種方法對問題進行50次求解，所得到的對地觀測衛星對目標區域進行觀測的兩個覆蓋指標(覆蓋率、總的覆蓋時間)以及各個算法求解的執行時間，分別求其平均值，如表3所示。

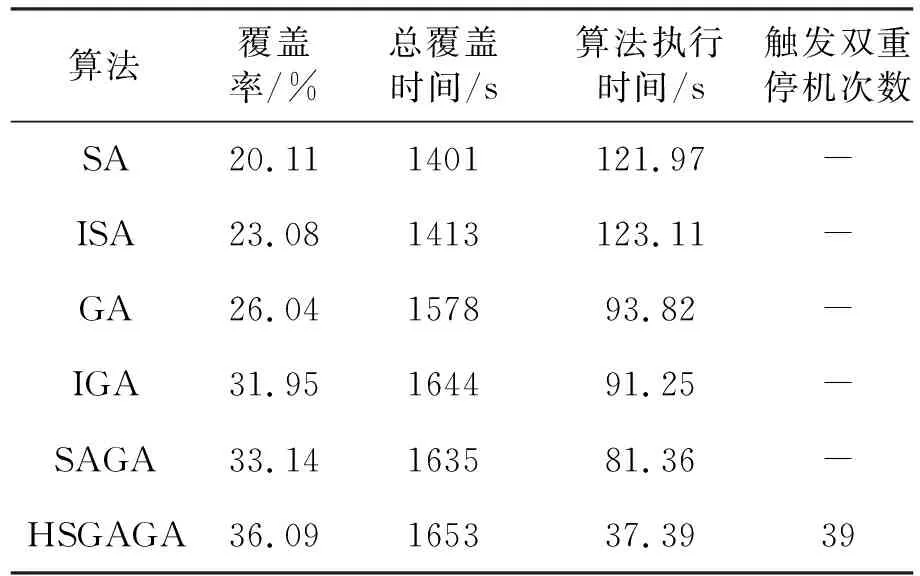
表3 各算法求解所得覆蓋性能及執行時間

由圖7、圖8和表3可以看出：

1)本文提出的HSGAGA算法執行了37.39 s，在287代時即達到全局最優解，而GA、IGA、SAGA算法分別執行了93.82 s、91.25 s、81.36 s，依然在1 000代仍進入了局部最優解，SA、ISA算法分別執行了121.97 s、123.11 s，依然在40 000次退火之后也仍進入了局部最優解。

2)應用HSGAGA算法對問題進行50次求解中，總共觸發了39次雙重停機條件，說明了在對問題進行優化求解中，使用雙重停機條件的必要性；并且，其所求得的全局最優解使得衛星對地覆蓋率達到了36.09%，比次好的SAGA算法高了2.95%；并且總的覆蓋時間1 653 s也是最高的，比次好的SAGA算法高了18 s；而且算法的執行時間也最短，為37.39 s，僅是次好的SAGA算法執行時間的45.96%。

結合圖8也可以看出，本文所設計的改進型自適應遺傳算法HSGAGA可以在種群初期充分利用種群的多樣性，通過交叉得到較好的個體，并且在種群中期，同時通過交叉和變異操作增加種群的多樣性，避免種群“早熟”而陷入局部最優，最后在種群末期，能夠以一定的變異率繼續進行全局尋優，避免了種群停滯不前。這也充分說明了本文所提出的HSGAGA算法對于解決復雜動態組合優化問題的快速性與有效性。

5 結束語

本文提出了一種改進型自適應遺傳算法(HSGAGA)，高效地解決了面向多星區域觀測調度問題。具體的實驗用例表明，相較于其他現代優化算法，HSGAGA算法所求得的側擺調度方案不但大大提高了衛星對目標區域進行觀測的覆蓋率和總的覆蓋持續時間，而且算法本身的執行時間很短，說明該算法既有效也高效。此外，該算法具有通用性，適用于其他動態組合調度優化問題的求解。

本文研究了只在垂直于星下點軌跡方向上側擺的衛星調度問題，后續的工作是進一步研究敏捷衛星(agile earth observation satellite, AEOS)對地觀測調度問題。