注漿、襯砌作用下非線性滲流隧洞彈塑性解
周 建,蔡 鍵,楊 帆,楊新安
(1.道路與交通工程教育部重點實驗室(同濟大學),上海 201804; 2.浙江溫州沈海高速公路有限公司,浙江 溫州 325000)
隨著中國公路、鐵路隧道的交通建設蓬勃發展,山嶺隧洞穿越富水環境的工況急劇增加[1-3],此環境中的深埋山嶺隧洞主要采取“堵水限排”支護設計準則[4-5],一般通過“注漿圈+襯砌”的堵水方式實現. 現階段,地下水在圍巖中的滲流特征尚不明朗,設計人員不能準確把握水壓隧洞支護設計[6]. 文獻[7]指出:要在堵水限排情況下進行襯砌結構設計研究,必須從理論上研究水作用下圍巖和襯砌結構的力學特征,弄清二者相互作用的機制,才能合理提供隧洞支護設計參數. 關于隧洞在滲流條件下圍巖與支護結構的作用理論解析國內外諸多學者進行了研究,如文獻[8]基于廣義有效應力原理,提出了水壓隧洞不同類型襯砌與圍巖作用的解析解;文獻[9]將數值試驗與解析解相結合,為深埋隧道在地下水包圍下初期支護與二次襯砌的初步設計提供了合理的途徑;文獻[10]研究了考慮襯砌和滲流場作用下海底隧道的彈塑性位移和應力解析解;文獻[11]推導了圍巖、注漿圈、襯砌和地下水共同作用下隧洞的彈塑性解,并提出了最優注漿圈厚度的確定方法;文獻[12]基于統一強度理論,給出隧洞滲流壓力、襯砌、注漿與巖體的相互作用的彈塑性解;以上支護設計研究均是基于達西定律基礎上進行的,部分試驗[13-14]表明:致密砂巖、破碎巖石等介質中的滲流呈現明顯的非達西流特征. 為了得到合理的支護設計,必須分析巖土材料的滲流屬于線性還是非線性,部分學者對非線性滲流進行了研究,如文獻[15]建立二次型高速非達西本構模型,預測了深埋隧洞的涌水量;文獻[16]開展了不同顆粒粒徑多孔介質在高水力梯度條件下的高速非線性滲流規律試驗研究,并確定了非線性滲流模型參數與顆粒粒徑之間的關系;文獻[17]建立巖體破壞突水非達西滲流模型,模擬了突水瞬態流動全過程,并認為巖體破壞突水問題采用非達西流模型計算十分必要;文獻[18]進行了切向位移作用下粗糙單裂隙的高速非達西滲流數值模擬分析,并給出了非線性滲流模型的經驗公式;文獻[19]建立了粗糙巖石裂隙低速非線性滲流模型并通過試驗驗證;文獻[20]建立了低滲透巖石非線性滲流的運動方程,并通過實驗數值驗證了所建立運動方程的正確性.
綜上所述,巖石滲流可能是低速非線性的、線性的,或是高速非線性的,這取決于地下水在圍巖中的分布和隧洞開挖巖體破壞程度. 目前,關于隧洞圍巖非線性滲流理論分析鮮少被關注,因此,亟待給出隧洞處于低速非線性滲流或是高速非線性滲流狀態下的彈塑性解析解,以便精確地指導隧洞支護設計. 本文將Izbash非線性滲流模型引入隧洞滲流理論,基于統一強度理論,推導深埋隧洞在注漿、襯砌作用下的應力場和位移場解析公式,并討論了非線性滲流對隧洞圍巖應力、位移和塑性區半徑的影響.
1 理論基礎
1.1 力學模型及基本假定
建立如圖1所示的圓形隧洞力學模型,并作出如下假定:1)深埋隧洞處于地下水包圍中;2)圍巖為均質﹑各向同性的連續介質;3)水流經圍巖和支護材料時流向以徑向為主;4)初始地應力為p0,rp、r3、r2和r1分別為塑性區半徑、襯砌內半徑、襯砌外半徑和注漿圈外半徑,rw為遠場水頭半徑,文獻[21]認為隧洞遠場水頭半徑rw一般大于30倍r1時,可保證工程精度,因此,可將隧洞在rw處的徑向應力視為p0,圍巖遠場、彈塑性區邊界、注漿圈外邊界、襯砌外邊界、襯砌內邊界的水頭分別為hw、hp、h1、h2和h3,圍巖、注漿圈和襯砌的滲透系數分別為k1、k2和k3,圍巖與注漿圈、注漿圈與襯砌、襯砌內邊界和塑性區邊界處的壓力分別為p1、p2、p3和pp.

圖1 力學模型
1.2 滲流場水頭分析
本文考慮的非線性滲流即圍巖(或注漿圈、襯砌)的水力梯度呈非線性變化,因圍巖遠場水壓與襯砌內水壓可確定,則在邊界處水頭[22]有
(1)
式中:hs為不同位置處的水頭,hs=ps/γ,其中ps為不同位置處的水壓力,γ為地下水重度. 水頭一般通過監測水壓并根據水頭、水壓的關系式獲得.
冪函數型Izbash方程因其公式簡單明了被廣泛應用于研究巖土材料的非線性滲流特征,Izbash方程的水力梯度公式[23]為
Js=Asvsms.
(2)
式中:s=1、2、3,分別代表圍巖、注漿圈和襯砌材料;J1、J2、J3分別為圍巖、注漿圈和襯砌內某點水力梯度;A1、m1為圍巖的水力梯度待定系數,A2、m2為注漿圈的水力梯度待定系數,A3、m3為襯砌的水力梯度待定系數,其中1﹤m1﹤2時,式(2)反映了顯著的慣性效應而導致的非線性滲流特征,當0﹤m1(或m2、m3)﹤1時,式(2)反映了低滲透巖石介質中固液界面效應導致的非線性滲流特征,而當m1(或m2、m3)=1時,式(2)服從達西定律;v1、v2、v3分別為圍巖、注漿圈、襯砌內某點滲流速度.
根據文獻[24],平面徑向滲流速度方程有
(3)
式中r為任意一點距離洞心的距離.
求解式(3),代入式(2)后等式兩邊積分,并根據Js=?hs/?r,可得
(4)
式中c1、c2均為待定系數.
當r1 (5) 式(5)為二元一次方程,可解出Asc1ms和c2,代入式(4)繼而求出hs. 同理,r2 (6) 統一強度理論自俞茂宏創立以來,廣泛應用于巖石、混凝土等拉壓特性不同的材料,彌補了Mohr-Coulomb準則未能考慮中間主應力致使計算結果偏于保守的遺憾. 統一強度理論在平面應變狀態下的表達式為 (7) 式中:σ1、σ3為第一主應力、第三主應力;c、φ為材料粘聚力、內摩擦角,ct、φt為材料統一粘聚力、內摩擦角,將圍巖、注漿圈和襯砌的粘聚力分別設為c1、c2和c3及內摩擦角分別設為φ1、φ2和φ3,則材料統一粘聚力可對應為ct1、ct2和ct3,材料統一內摩擦角對應為φt1、φt2和φt3;b為參數,反映中間主應力對材料強度的影響程度,取值為0≤b≤1,b的具體值可根據材料的力學試驗確定. 假設σθ(徑向有效應力)>σr(切向有效應力),令σ1=σθ、σ3=σr,則式(7)中第1式可改寫為 (8) 根據彈性力學理論,材料考慮滲透力時的平衡微分方程為 (9) 幾何方程為 (10) 式中u為材料的徑向位移. 彈性區服從虎克定律的平面應力應變方程為 (11) 式中:Ej、μj分別為彈性模量和泊松比,且圍巖、注漿圈和襯砌的彈性模量分別為E1、E2、E3,圍巖、注漿圈和襯砌的泊松比分別為μ1、μ2、μ3. 將式(9)與式(11)聯立,并根據邊界條件σr|r=rw=-p0,σr|r=r1=-p1,σr|r=r2=-p2,σr|r=rp=-pp,圍巖、注漿圈和襯砌有彈性位移分別為 (12) (13) (14) 其中hp在所處材料中按照差值法計算. 將式(12)~(14)代入式(11),則圍巖、注漿圈和襯砌徑向、切向應力分別為 (15) (16) (17) 將式(8)與式(9)聯立,并根據邊界條件σr|r=r3=-p3,則襯砌內塑性徑向、切向應力分別為 (18) 式中 假定材料塑性階段體積應變為0,根據幾何方程式(10),則襯砌塑性區位移為 (19) 聯立式(12)~(14),并根據位移在邊界處連續: u11|r=r1=u12|r=r2. (20) 可求得p1和p2. 將襯砌內壓p3視為0,由徑向應力連續: σr3|r=rp=σrp4|r=rp. (21) 可求得rp,從而獲得圍巖應力,下文參照此法求p1、p2和rp. 圍巖仍處于彈性狀態,則圍巖位移u21=u11,圍巖徑向、切向應力σr21=σr11、σθ21=σθ11. 將式(9)代入式(11),根據邊界條件σr|r=r1=-p1,σr|r=rp=-pp,注漿圈彈性部分位移為 (22) 材料塑性階段位移參照式(19),則注漿圈、襯砌塑性部分位移分別為 (23) (24) 將式(22)代入式(11),將式(8)代入式(9),并根據邊界條件σr|r=r2=-p2、σr|r=r3=-p3,注漿圈彈性部分、注漿圈塑性部分和襯砌的徑向、切向應力分別為 (25) (26) (27) 式中: 將式(9)與式(11)聯立,并根據邊界條件σr|r=rw=-p0,σr|r=rp=-pp,圍巖彈性位移有 (28) 式中: 材料塑性階段位移參照式(19),則圍巖、注漿圈和襯砌塑性部分位移分別為 (29) (30) (31) 將式(28)代入式(11),圍巖彈性部分徑向、切向應力分別為 (32) 將式(8)代入式(9),并根據邊界條件σr|r=r2=-p2、σr|r=r3=-p3,圍巖塑性部分和注漿圈的徑向、切向應力分別為 (33) (34) 式中: 襯砌的徑向、切向應力與式(27)相同,即σrp34=σrp24、σθp34=σθp24. 為了驗證本文的理論解答,借助文獻[15]實例參數,隧洞襯砌內半徑r1=4 m、外半徑r2=5 m,注漿圈外半徑r3=5.2 m,初始地應力p0=10 MPa,遠場水頭半徑rw=200 m,α=1,遠場水壓力pw=1 MPa,地下水重度γ=10 kN/m3,h1=50 m,h2=h3=0 m,圍巖、注漿圈和襯砌參數見表1. 理論計算時,將隧道已知參數代入上述公式,當求得塑性區半徑rp與某一種彈塑性邊界情況一致時,則位移場與應力場按照該情況計算. 利用ABAQUS有限元軟件模擬文獻[15]工況,為了減少模型邊界效應,建立模型如圖3所示,模型為210 m×210 m監測斷面為隧洞縱向中心斷面. 為模擬隧洞的非線性滲流,根據地下水流速公式: ksJs=vs, (35) 式中ks為材料的滲透系數, 并結合式(2)可得 表1 圍巖、注漿圈和襯砌參數 圖2 隧道模型圖 (36) 假設在隧洞遠端的滲流速度vs和水力梯度參數As一定,且取vs為1×10-4m/s,根據式(36),可得m1=0.5、m1=1.5的圍巖等效滲透系數分別為5×10-6m/s、0.05 m/s,則隧洞監測斷面洞壁的位移、切向應力的數值解與本文理論解對比見表2、3. 表2 隧洞洞壁位移對比 表3 隧洞切向應力對比 從表2可以看出,本文理論解較數值解略大,隨著m1增大,洞壁位移誤差在8.8%以內,隧洞切向應力誤差最大為14.1%,理論解與數值解吻合性較好,驗證了理論解的可靠性. 一般來說,材料的滲透系數越小,水流穿過材料裂隙的難度越大,水力梯度待定系數越小,由于表1中注漿圈和襯砌的滲透系數遠小于圍巖,不難判斷,m1值大于m2和m3,假設m2=m3,分析非線性滲流對隧洞塑性區半徑、圍巖應力和位移的影響,如圖3、4、5所示. 圖3 本文方法得到的塑性區半徑與Li解對比圖 圖4 考慮非線性滲流的隧洞應力分布 從圖3可以看出,隨著b值增大,塑性區半徑rp逐漸減小且最大減小幅度為13.2%,而工程實踐中rp的精確性直接影響支護結構設計,說明考慮中間主應力是必要的,否則誤差較大;m1對rp值的影響遠大于m2和m3,且m1越大rp越大. 根據上述分析,圖4僅探討m1對圍巖應力的影響,因此假定m2=m3=0.4. 當b=0.4時,隨著m1越大,圍巖徑向、切向應力越小. 結合圖3和圖4,當m1=1.0、m2=m3=0.4時,圍巖滲流服從達西定律,塑性區半徑、圍巖應力與文獻[15]較為接近,從而進一步驗證了本文理論方法的可行性. 綜上所述,當圍巖滲流為高滲透性非線性滲流時,若采用達西定律則低估塑性區半徑、高估實際圍巖應力,不利于支護設計;圍巖滲流為低滲透性非線性滲流時,達西定律計算得到塑性區半徑偏大、圍巖應力偏保守. 圖5顯示了b=0.4時隧洞位移與支護厚度的關系,D1、D2分別為注漿圈、襯砌厚度,當支護厚度一定時,圍巖滲流從低滲透性非線性滲流向高滲透性非線性滲流轉變時,隧洞位移逐漸增大,因此,當隧洞圍巖處于高水壓、突水嚴重地層時,傳統的達西定律計算的洞壁位移偏于保守,不利于隧洞施工安全. 另外,隨著注漿圈和襯砌厚度的增大,洞壁位移能夠得到有效控制,但襯砌厚度超過1 m時,洞壁位移的控制并不顯著,則支護設計時應合理設定支護材料厚度,以免造成較大浪費. 圖5 隧洞位移與支護厚度曲線 1)在注漿、襯砌支護條件下,基于Izbash非線性滲流模型,求得圍巖及支護材料的水頭分布,并運用統一強度理論,推導了塑性區在不同材料位置時的應力和位移彈塑性解. 2)考慮非線性滲流的理論位移解較等效后的ABAQUS解略大,切向應力誤差在允許范圍之內,吻合性較好;中間主應力和圍巖的水力梯度系數m1對隧洞塑性區半徑的影響顯著,而對圍巖應力的影響較塑性區半徑略小. 3)圍巖水力梯度系數m1對隧洞位移的影響不容忽視,當隧洞圍巖處于高速非線性滲流時,達西定律計算的隧洞位移偏保守,體現了研究非線性滲流作用下隧洞彈塑性分析的重要意義;另外,不能盲目追求安全性而增加支護材料厚度,否則導致支護不經濟.1.3 統一強度理論
2 非線性滲流作用下的隧洞圍巖應力、位移分析

2.1 彈塑性交界處位于襯砌內


2.2 彈塑性交界處位于注漿圈內


2.3 彈塑性交界處位于圍巖內


3 實例驗證



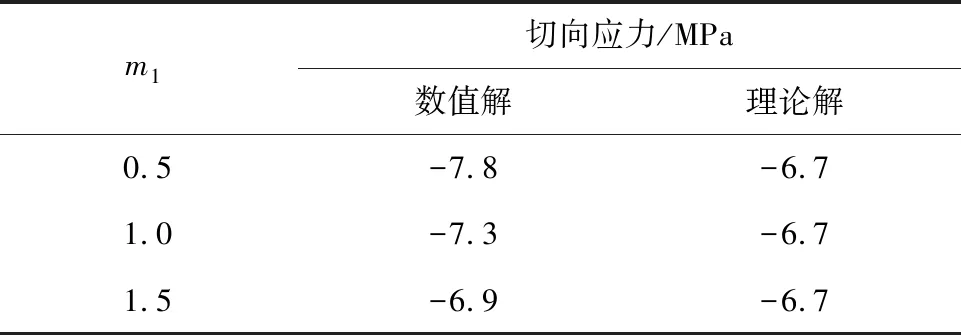
4 非線性滲流對隧洞塑性區半徑、圍巖應力和位移的影響



5 結 論

