受剪應(yīng)力影響的CFRP-鋼界面蠕變本構(gòu)模型

徐佰順，姚亞東，常建梅，張長江，宋 帥

(1. 內(nèi)蒙古大學(xué) 交通學(xué)院，呼和浩特 010070；2.內(nèi)蒙古自治區(qū)橋梁檢測與維修加固工程技術(shù)研究中心，呼和浩特 010070；3.青島理工大學(xué) 土木工程學(xué)院, 山東 青島 266033)

CFRP具有重量輕、強(qiáng)度高、易于加工成形、便于施工、耐腐蝕等優(yōu)點(diǎn)，廣泛用于混凝土結(jié)構(gòu)及鋼結(jié)構(gòu)的加固補(bǔ)強(qiáng)工程中[1-2]. 黏貼CFRP加固鋼結(jié)構(gòu)技術(shù)通過膠粘劑將CFRP片材與鋼材連接成一體共同受力.該技術(shù)鋼材不需要開孔或焊接，避免了焊接連接引起的焊接殘余應(yīng)力或栓接連接導(dǎo)致的截面削弱[3]. CFRP與鋼材之間的黏結(jié)界面是整個(gè)加固體系的薄弱環(huán)節(jié)，其黏結(jié)性能是加固成功的關(guān)鍵，這方面學(xué)者們已經(jīng)開展了大量卓有成效的試驗(yàn)研究[4-6]和理論分析[7-8]，包括界面黏結(jié)失效形式、黏結(jié)滑移本構(gòu)關(guān)系、極限承載力計(jì)算方法和數(shù)值模擬分析等.在長期荷載作用下，結(jié)構(gòu)加固工程中常用的膠粘劑表現(xiàn)出黏彈性特性[9]，既有固體的彈性又有流體的黏性. 膠粘劑隨時(shí)間而變化的變形過程，主要表現(xiàn)為蠕變和應(yīng)力松弛. 膠粘劑的蠕變變形會導(dǎo)致加固結(jié)構(gòu)界面發(fā)生內(nèi)力重分布[10]，致使黏結(jié)界面發(fā)生蠕變損傷，這種損傷會影響?zhàn)そY(jié)界面的黏結(jié)性能[3,11]. 在CFRP加固體系中若要明確膠粘劑的黏彈性特性對加固結(jié)構(gòu)影響，關(guān)鍵在于得到準(zhǔn)確表征膠粘劑剪切蠕變行為的黏彈性本構(gòu)方程.

近年來研究者們對CFRP-混凝土單面搭接試件或雙面搭接試件進(jìn)行長期加載試驗(yàn)，并考慮多種因素影響以獲得表征膠粘劑蠕變變形的本構(gòu)模型.文獻(xiàn)[12]認(rèn)為界面剪應(yīng)力水平和膠層厚度對膠粘劑蠕變行為有顯著影響. 文獻(xiàn)[13]在文獻(xiàn)[12]研究基礎(chǔ)上引入了膠粘劑養(yǎng)護(hù)齡期的影響，采用改進(jìn)的Maxwell模型和Findley冪律方程預(yù)測界面的蠕變變形.文獻(xiàn)[14]采用廣義的Maxwell模型預(yù)測界面的蠕變變形以及界面的蠕變斷裂發(fā)展. 文獻(xiàn)[15]和文獻(xiàn)[16]應(yīng)用時(shí)間-溫度等效原理(TTSP)，通過短時(shí)間高溫條件下雙剪試件拉伸蠕變試驗(yàn)獲得界面的黏彈性特性，并用串聯(lián)的標(biāo)準(zhǔn)線性固體模型模擬界面的蠕變變形. 文獻(xiàn)[17]利用TTSP原理進(jìn)行了短期膠體拉伸蠕變試驗(yàn)得到了Burgers本構(gòu)模型，基于此模型對持續(xù)拉伸荷載作用下CFRP-混凝土雙剪試件進(jìn)行了試驗(yàn)驗(yàn)證和有限元分析.

在CFRP加固鋼結(jié)構(gòu)方面，文獻(xiàn)[10]采用有限元分析方法研究了膠粘劑黏彈性對CFRP-鋼界面應(yīng)力的影響，考慮膠粘劑黏彈性后，界面剪應(yīng)力和剝離應(yīng)力隨時(shí)間增加而減小.本文對CFRP-鋼雙剪試件進(jìn)行了長期蠕變試驗(yàn)，采用Burgers模型和Findley冪律方程表征CFRP-鋼界面膠粘劑的剪切蠕變行為，基于Burgers模型特性及膠層剪應(yīng)變-時(shí)間曲線推導(dǎo)了各參數(shù)的求解方法，結(jié)合試驗(yàn)結(jié)果進(jìn)行了擬合分析，得到了本構(gòu)模型中考慮剪應(yīng)力影響的各參數(shù)表達(dá)式，并對模型的預(yù)測結(jié)果進(jìn)行了對比和驗(yàn)證.

1 黏彈性本構(gòu)模型

1.1 Burgers模型

圖1所示為典型的Burgers模型，該模型屬于流變力學(xué)模型的一種，具有概念清晰以及物理意義明確的特點(diǎn).Burgers模型由Maxwell模型和Kelvin模型串聯(lián)而成.Maxwell模型由“彈簧”元件和“黏壺”元件串聯(lián)而成，GM為剪切彈性模量，ηM為黏度系數(shù).Kelvin模型由“彈簧”元件和“黏壺”元件并聯(lián)而成，GK為剪切彈性模量，ηK為黏度系數(shù).

圖1 Burgers模型

在恒定的剪應(yīng)力τ0作用下，任意t時(shí)刻Burgers模型的總應(yīng)變γ(t)可表示成3部分：Maxwell模型中“彈簧”元件的剪切彈性應(yīng)變γ1和“黏壺”元件的黏性應(yīng)變γ2(t)，Kelvin模型的延遲彈性應(yīng)變γ3(t).根據(jù)流變力學(xué)理論γ1、γ2(t)、γ3(t)的表達(dá)式分別為

γ1=τ0/GM，

(1)

(2)

(3)

式中：γ1為瞬時(shí)彈性應(yīng)變，γ2(t)和γ3(t)的和為蠕變應(yīng)變.

t時(shí)刻的總應(yīng)變γ(t)為

γ(t)=γ1+γ2(t)+γ3(t).

(4)

將式(1)～(3)代入式(4)得

(5)

在正常使用階段的荷載作用下，黏彈性材料的應(yīng)變-時(shí)間關(guān)系如圖2所示.在加載瞬間黏彈性材料產(chǎn)生瞬時(shí)彈性應(yīng)變，此時(shí)為彈性階段.隨后加載大小不變而應(yīng)變隨時(shí)間逐漸增加，增加的應(yīng)變即為蠕變應(yīng)變，大致可分為兩個(gè)階段：一個(gè)是過渡蠕變階段，在此階段黏彈性材料的應(yīng)變速率(曲線的斜率)隨加載時(shí)間的增加而不斷降低；一個(gè)是穩(wěn)態(tài)蠕變階段，在此階段曲線基本為一條直線，即曲線的斜率保持不變，也就是說蠕變應(yīng)變與加載時(shí)間成正比例關(guān)系.

圖2 應(yīng)變-時(shí)間關(guān)系

根據(jù)Burgers模型特性以及黏彈性材料的應(yīng)變-時(shí)間關(guān)系曲線特點(diǎn)，可通過下列步驟逐步求解Burgers模型的各參數(shù).

步驟1將加載時(shí)間t=0，代入式(5)中得，瞬時(shí)彈性應(yīng)變γe為

γe=τ0/GM.

(6)

對應(yīng)于圖2中的彈性階段，式(6)變換后可得參數(shù)GM=τ0/γe.

(7)

在式(7)中取t= 0，有γ(0)=τ0/GM+τ0/GK，表示穩(wěn)態(tài)蠕變階段曲線的延長線與應(yīng)變軸的交點(diǎn)到原點(diǎn)的距離，如圖2所示.在步驟1中求得參數(shù)GM后，繼而可求參數(shù)GK.

步驟3對式(5)求導(dǎo)，得

(8)

(9)

式(9)表示穩(wěn)態(tài)蠕變階段曲線的斜率k=τ0/ηM，如圖2所示.根據(jù)曲線斜率k，可求參數(shù)ηM=τ0/k.

步驟4當(dāng)t= 0時(shí)，式(8)簡化為

(10)

式(10)表示過渡蠕變階段曲線的初始應(yīng)變速率為tanα=(τ0/ηK+τ0/ηM)，如圖2所示.在步驟3中求得參數(shù)ηM后，繼而可求參數(shù)ηK.

1.2 Findley冪律方程

Findley冪律方程最早是由Findley[18]提出的.因其公式簡單，參數(shù)較少，在表征高分子聚合物的黏彈性方面應(yīng)用廣泛.Findley冪律方程的剪切應(yīng)變γ(t)形式為

γ(t)=γ0+m·tn.

(11)

式中:γ(t)為時(shí)間為t時(shí)的總剪應(yīng)變;γ0為初始彈性剪應(yīng)變;m和n為相關(guān)系數(shù)，由試驗(yàn)結(jié)果確定.

2 長期加載試驗(yàn)

2.1 試件設(shè)計(jì)及制作

試驗(yàn)采用的鋼板為熱軋Q235B，寬度為50 mm，長度為300 mm，厚度為6 mm，抗拉強(qiáng)度為309 MPa，彈性模量為190 GPa. CFRP布采用密度為300 g/mm2的東麗UT70-30型，寬度為30 mm，長度為420 mm，厚度為0.167 mm，抗拉強(qiáng)度為3 920 MPa，彈性模量為237 GPa，伸長率為1.71%. 膠粘劑采用愛牢達(dá)XH 180型，抗拉強(qiáng)度為47 MPa，彈性模量為2.86 GPa鋼-鋼拉伸抗剪強(qiáng)度為16 MPa，伸長率為1.90%.

為方便試驗(yàn)加載及有效采集試驗(yàn)數(shù)據(jù)，試驗(yàn)中采用雙剪試件. 試件制作時(shí)首先用電砂輪打磨鋼板除去表面銹跡和油污，并用800目砂紙磨掉表面毛刺，用丙酮擦拭鋼板，待干燥后用毛刷均勻地涂抹膠粘劑，利用刮板均勻擠壓CFRP布趕出氣泡. 制作好一面后，24 h后再黏貼另一面. 待試件制作完成后，在實(shí)驗(yàn)室條件下養(yǎng)護(hù)7 d.

試件尺寸及應(yīng)變片布置如圖3所示.試件每面各布置12個(gè)應(yīng)變片，每個(gè)試件黏貼24個(gè)應(yīng)變片.為方便試驗(yàn)結(jié)果表達(dá)，將測試面分別定義為Q面和H面，應(yīng)變片編號從加載端到固定端依次定義為Q0#～Q11#及H0#～H11#.其中編號Q0#和H0#兩個(gè)應(yīng)變片位于兩塊鋼板空隙處的CFRP布上.

圖3 CFRP-鋼板雙剪試件及應(yīng)變片布置(mm)

2.2 試驗(yàn)方案及加載裝置

試驗(yàn)共設(shè)計(jì)并制作27個(gè)CFRP-鋼雙剪試件. A組3個(gè)試件，待養(yǎng)護(hù)完成后進(jìn)行靜力破壞試驗(yàn)，得到極限承載力Pu分別為27.4、28.8、31.6 kN，Pu平均值為29.3 kN，標(biāo)準(zhǔn)差為2.1. 平均極限剪切強(qiáng)度τu=Pu/(2bclc)， 其中bc為CFRP寬度30 mm，lc為CFRP黏結(jié)長度200 mm，可計(jì)算得到τu=2.44 MPa. B、C、D、E組每組6個(gè)試件，持續(xù)施加的界面名義剪應(yīng)力τ0分別取0.22τu、0.44τu、0.60τu和0.73τu，即分別為0.54、1.07、1.46、1.78 MPa.試驗(yàn)的分組情況、黏結(jié)界面上長期施加的界面名義剪應(yīng)力τ0和加載時(shí)間見表1.

長期加載采用自制的加載裝置，與文獻(xiàn)[19]一樣.該裝置根據(jù)杠桿原理制作，整個(gè)裝置由底梁、立柱、橫梁組成，底梁與立柱通過焊接連接，立柱與橫梁通過螺栓連接.橫梁一端加載重物，一端連接試件，為減小重物的重量，兩力臂的比值為10∶1. 重物為澆筑的立方體混凝土塊. 一個(gè)底梁對稱分布兩套加載裝置，兩套裝置之間通過與立柱焊接的連接桿進(jìn)行連接以保證結(jié)構(gòu)的穩(wěn)定性. 不同重量的混凝土塊進(jìn)行組合后，通過絲桿串聯(lián)，絲桿頂部采用花籃螺栓與加載橫梁相連. 通過調(diào)節(jié)旋緊花籃螺栓的速度，可以控制加載重物的提升速度，以保證勻速加載.

表1 試件分組

2.3 試驗(yàn)結(jié)果

2.3.1 CFRP表面應(yīng)變分布

試件B22D90、C44D90、D60D90、E73D90的CFRP表面應(yīng)變分布(每組僅示出一個(gè)試件)如圖4所示.觀察各圖中CFRP應(yīng)變分布曲線可知，在荷載作用下僅在測點(diǎn)Q1#～Q5#范圍內(nèi)CFRP布應(yīng)變響應(yīng)較大，測點(diǎn)Q1#(加載端部)應(yīng)變值最大，距測點(diǎn)Q1#越遠(yuǎn)，應(yīng)變值急劇減小，測點(diǎn)Q5#后各測點(diǎn)應(yīng)變較小.表明荷載僅在CFRP-鋼界面端部一部分區(qū)域內(nèi)傳遞，且CFRP應(yīng)變呈現(xiàn)非線性減小.對比圖中同一測點(diǎn)在不同加載時(shí)間的應(yīng)變數(shù)值，可知隨著加載時(shí)間的增加，測點(diǎn)Q1#～Q5#范圍應(yīng)變數(shù)值逐漸增大.

(a) B22D90 Q面

(b) C44D90 Q面

(c) D60D90 Q面

(d) E73D90 Q面

2.3.2 CFRP各測點(diǎn)應(yīng)變隨時(shí)間變化

為更直觀表達(dá)各測點(diǎn)應(yīng)變隨加載時(shí)間的變化情況，將圖4中試件C44D90、D60D90、E73D90(試件B22D90應(yīng)變變化較小)測點(diǎn)Q1#、Q2#、Q3#在整個(gè)試驗(yàn)周期內(nèi)的應(yīng)變數(shù)值進(jìn)行整理如圖5所示.由圖5可知，測點(diǎn)Q1#、Q2#、Q3#的應(yīng)變值均隨著加載時(shí)間的增加而增大.各組曲線具有相似的特點(diǎn)，由3個(gè)階段組成，以圖5中(b)圖中測點(diǎn)Q1#為例，第1階段，圖中OA段，荷載施加瞬時(shí)CFRP發(fā)生彈性變形，應(yīng)變與荷載大小成正比；第2階段，圖中AB段，彈性變形完成后，CFRP應(yīng)變隨著時(shí)間的增加逐漸增大，但增大速率不斷減小，即曲線斜率變小；第3階段，圖中BC段，應(yīng)變增大速率減小到一定值后，在剩余試驗(yàn)周期內(nèi)基本不發(fā)生變化或變化很小.圖5中CFRP應(yīng)變隨時(shí)間變化關(guān)系與圖7中膠粘劑的剪應(yīng)變-時(shí)間關(guān)系曲線具有相似特性，即應(yīng)變在前期增大較快，后期增大逐漸減緩，最后應(yīng)變增加速率保持不變.這是因?yàn)樵诔掷m(xù)荷載作用下膠粘劑層發(fā)生了蠕變變形，致使試件發(fā)生了內(nèi)力重分布，表現(xiàn)為CFRP應(yīng)變增加，為保持受力平衡與膠粘劑層臨近的鋼板表面應(yīng)變應(yīng)減小.

另外，經(jīng)過2 160 h后，試件C44D90、D60D90和E73D90測點(diǎn)Q1#的蠕變應(yīng)變(總應(yīng)變減去第1階段彈性應(yīng)變)與彈性應(yīng)變比值的分別為0.122、0.153和0.206，表明在測試周期內(nèi)CFRP應(yīng)變分別增加了12.2%、15.3%和20.6%.說明界面名義剪應(yīng)力τ越大，膠粘劑蠕變變形就越大，CFRP應(yīng)變增加的就越多.

(a) C44D90 Q面

(b) D60D90 Q面

(c) E73D90 Q面

3 膠粘劑層的剪切變形

CFRP-鋼雙面搭接試件在受到拉伸荷載作用后，膠層的變形如圖6所示.

圖6 膠層剪切荷載作用

由圖6中的幾何關(guān)系可知，加載瞬時(shí)γ0為

γ0=Y0/ta.

(12)

式中：ta為膠層的厚度，γ0為加載瞬時(shí)膠層的剪應(yīng)變，Y0為膠層上、下表面的之間相對變形.

隨著加載時(shí)間的增加膠粘劑將發(fā)生蠕變，則γ(t)為

γ(t)=Y(t)/ta，

(13)

式中：γ(t)為t時(shí)刻膠層總的剪應(yīng)變，Y(t)為膠層上、下表面的總的相對變形.

假設(shè)CFRP-膠粘劑界面不發(fā)生相對滑動(dòng)且CFRP全截面上應(yīng)變不變，對CFRP表面應(yīng)變進(jìn)行積分可得Y(t)為

(14)

式中ε(x)為CFRP表面應(yīng)變.

本試驗(yàn)中測得的CFRP表面應(yīng)變是不連續(xù)的，可通過數(shù)值積分的方法近似計(jì)算Y(t)[20]為

(15)

式中：εc,i為第i個(gè)CFRP表面應(yīng)變測點(diǎn)的數(shù)值，Li為第i個(gè)CFRP表面應(yīng)變測點(diǎn)到加載端的距離.

結(jié)合式(13)和式(15)，可以得到任意t時(shí)刻γ(t)為

(16)

根據(jù)長期加載試驗(yàn)實(shí)測數(shù)據(jù)，可通過式(16)得到膠層剪應(yīng)變與加載時(shí)間的關(guān)系.試件B22D90、C44D90、D60D90、E73D90的膠層剪應(yīng)變隨時(shí)間變化(每組僅示出1個(gè)試件)如圖7所示.觀察圖7中各條曲線可知，曲線特征與圖2類似，可分為3個(gè)階段：彈性階段、過渡蠕變階段和穩(wěn)態(tài)蠕變階段.

圖7 膠層剪應(yīng)變與加載時(shí)間關(guān)系

4 模型參數(shù)的求解與驗(yàn)證

4.1 Burgers模型參數(shù)

根據(jù)第2節(jié)的試驗(yàn)結(jié)果及式(16)，可得各組試件膠層剪應(yīng)變隨時(shí)間變化曲線，結(jié)合第1節(jié)中Burgers模型中各參數(shù)的求解方法，可得到Burgers模型中各參數(shù)的數(shù)值.GM通過式(6)計(jì)算得25.44 MPa，其他參數(shù)見表2. 表2中各參數(shù)求解時(shí)以各組試件的Q面應(yīng)變數(shù)據(jù)為依據(jù).

表2 Burgers模型計(jì)算結(jié)果

以表2中參數(shù)ηM、GK和ηK的數(shù)值為縱坐標(biāo)，各組試件的界面名義剪應(yīng)力τ為橫坐標(biāo)繪制Burgers模型參數(shù)與名義剪應(yīng)力關(guān)系曲線，如圖8所示.由圖8可看出，各組試件參數(shù)ηM、GK和ηK的數(shù)值的大小與界面名義剪應(yīng)力有一定關(guān)系.根據(jù)最小二乘法原理，采用MATLAB實(shí)現(xiàn)曲線擬合得到參數(shù)ηM、GK和ηK與界面名義剪應(yīng)力τ的函數(shù)關(guān)系分別為

ηM(τ)=-29 728τ+783 379，

(17)

GK(τ)=-10τ+25.5，

(18)

ηK(τ)=254.3τ2-633.4τ+637.2.

(19)

則Burgers模型的表達(dá)式為

(20)

圖8 Burgers模型參數(shù)與名義剪應(yīng)力關(guān)系

4.2 Findley冪律方程

根據(jù)各組試件膠層剪應(yīng)變隨時(shí)間變化曲線，同樣可采用最小二乘法回歸分析得到Findley冪律方程中的參數(shù)，結(jié)果見表3. 從表3中可知，各組試件的m與n大小不同，說明界面名義剪應(yīng)力的大小對參數(shù)有影響.參數(shù)m、n與界面名義剪應(yīng)力τ的關(guān)系如圖9所示.采用MATLAB對數(shù)據(jù)進(jìn)行擬合分析，可得到參數(shù)m與n為因變量，剪應(yīng)力τ為自變量的函數(shù)方程為

m(τ)=0.045 5τ-0.017 6,

(21)

n(τ)=0.059 9τ2-0.14τ+0.287 8.

(22)

4.3 本構(gòu)模型的校核

在得到Burgers模型和Findley冪律方程各參數(shù)表達(dá)式后，為檢驗(yàn)兩類模型的預(yù)測能力，采用H面的試驗(yàn)結(jié)果進(jìn)行驗(yàn)證.通過均方根誤差(RMSE)的大小反映預(yù)測值與試驗(yàn)值的偏離程度，RMSE越小表示模型的預(yù)測精度越高.RMSE的表達(dá)式為

(23)

圖9 Findley冪律方程參數(shù)與名義剪應(yīng)力關(guān)系

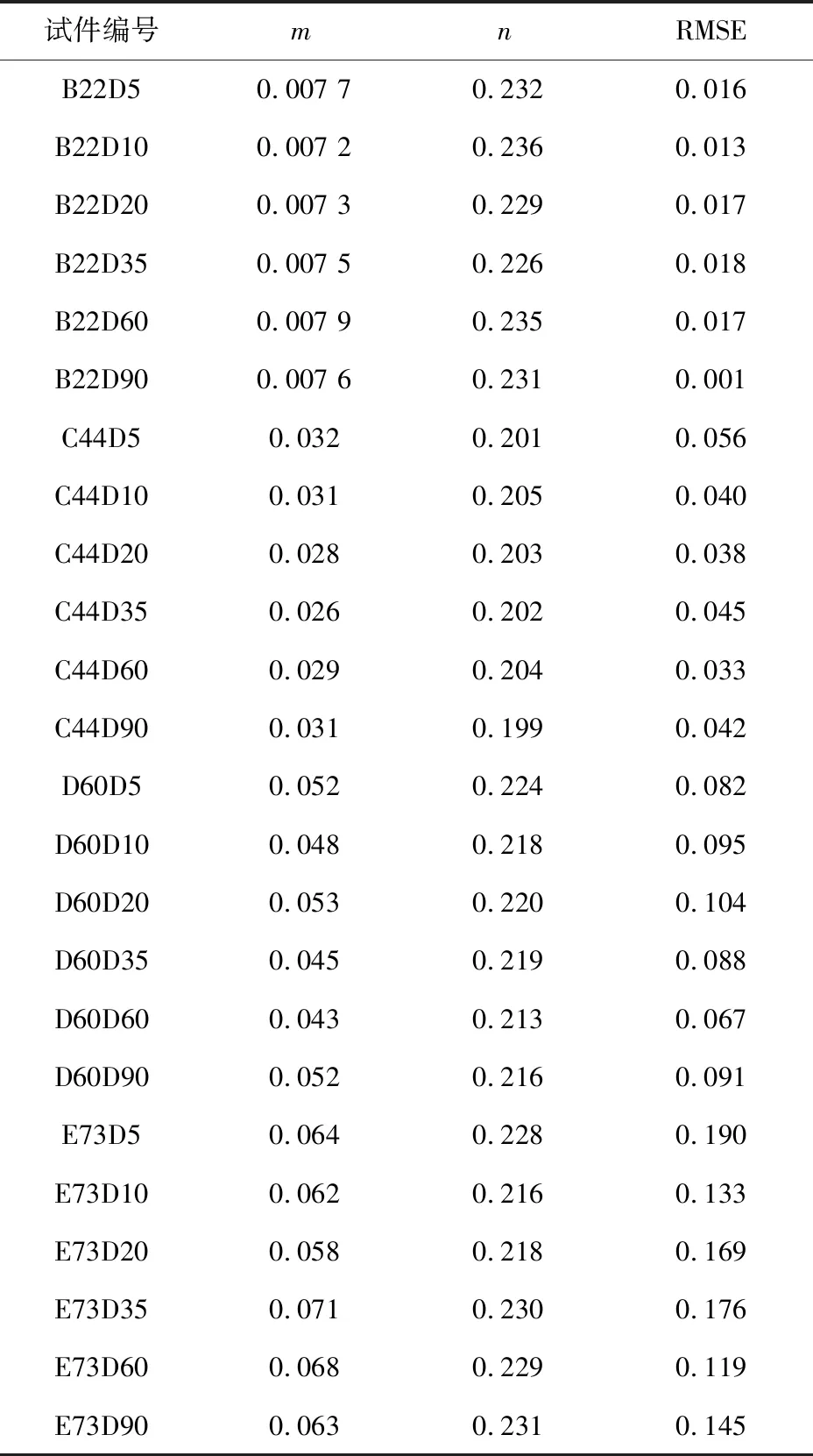
表3 Findley冪律方程計(jì)算結(jié)果

選取試件B22D20、C44D60、D60D35和E73D60作為每組的代表，將膠層剪應(yīng)變的試驗(yàn)值、Burgers模型的預(yù)測曲線及Findley冪律方程的預(yù)測曲線繪制于圖10中.由圖10可知，兩類模型的RMSE均較小，表明模型預(yù)測值與試驗(yàn)值偏離較小，兩類模型都可以很好地預(yù)測CFRP-鋼界面的剪切蠕變變形.

(a)B組與D組試件

(b)C組與E組試件

各組試件膠層剪應(yīng)變Burgers模型的預(yù)測值與H面試驗(yàn)值之間的RMSE見表2，F(xiàn)indley冪律方程的預(yù)測值與H面試驗(yàn)值之間的RMSE見表3.對比表2與表3中的RMSE大小可知，Burgers模型得到的RMSE普遍小于Findley冪律方程得到的RMSE，尤其對于D組和E組試件表現(xiàn)更為明顯.這可能是因?yàn)镕indley冪律方程中參數(shù)m擬合方程的R2較小，即擬合曲線對觀測值的擬合程度一般，D組和E組試件的界面名義剪應(yīng)力較高，這種影響就會越大.說明對于CFRP-鋼界面膠粘劑的剪切蠕變變形的表征上Burgers模型要優(yōu)于Findley冪律方程.這點(diǎn)也可從圖10中直觀看出，Burgers模型的預(yù)測曲線更接近于試驗(yàn)值.

5 結(jié) 論

1)在長期界面剪切應(yīng)力作用下CFRP-鋼界面膠粘劑發(fā)生了蠕變變形.膠層蠕變導(dǎo)致黏結(jié)界面發(fā)生了內(nèi)力重分布，直觀表現(xiàn)為同一位置處CFRP應(yīng)變隨加載時(shí)間增加而增大，CFRP應(yīng)變前期增大較快，后期增大較慢.另外，不同組試件之間對比發(fā)現(xiàn)界面名義剪應(yīng)力τ越大，膠粘劑蠕變變形就越大，CFRP應(yīng)變增加的就越多.

2)可采用Burgers模型和Findley冪律方程表征剪應(yīng)力作用下CFRP-鋼界面膠粘劑的蠕變變形.兩類本構(gòu)模型中參數(shù)與界面剪應(yīng)力τ的大小有一定關(guān)系. Burgers模型中參數(shù)ηM和GK均與剪應(yīng)力τ具有線性關(guān)系，參數(shù)ηK是剪應(yīng)力τ的二次函數(shù). Findley冪律方程中參數(shù)m是剪應(yīng)力τ的一次函數(shù)，參數(shù)n是剪應(yīng)力τ的二次函數(shù).

3)Burgers模型和Findley冪律方程的RMSE均較小，即預(yù)測值與試驗(yàn)值偏離較小，說明兩類模型都可以很好地預(yù)測CFRP-鋼界面的剪切蠕變變形.相對而言，Burgers模型的RMSE要小于Findley冪律方程的RMSE，尤其是當(dāng)界面剪應(yīng)力較高時(shí)更為明顯，說明Burgers模型預(yù)測的CFRP-鋼界面膠粘劑蠕變變形與試驗(yàn)結(jié)果吻合更好.