腐蝕電場的力學化學耦合模型

徐慶林，王向軍，童余德，宋玉蘇

(1.海軍工程大學 電氣工程學院，武漢 430033；2.海軍工程大學 基礎部，武漢 430033)

艦船腐蝕及防腐電流在其附近產生的電流場稱為艦船腐蝕電場[1]，隨著水下電場探測技術的不斷發展，艦船腐蝕電場已成為一種新型的水下信號源[2-3]. 目前，艦船腐蝕電場主要有實船測量、物理縮比模型等實驗研究方法和等效電偶極子模型、邊界元等仿真研究方法，實驗研究不僅成本高、周期長，且難以測得艦船周圍全空間的電場分布. 邊界元法是一種非常適合求解開域問題的高精度數值計算方法[4]，已被廣泛應用于石油鉆井平臺、艦船等海洋結構件的腐蝕防護技術的仿真[5-6]，近年來，已有學者將其應用于艦船腐蝕電場的仿真研究[7-9]. 學者們研究了海床電導率、海水電導率、溫度、流速、深度等海洋環境因素對艦船腐蝕電場的影響[2,10-11]，建立了艦船腐蝕電場等效電偶極子模型，并分析了水平和垂直電偶極子在多層介質中產生的電磁場[12-14].

船舶和海洋工程結構的復雜性及其服役環境的特殊性，使得結構產生復雜的應力應變，如肋骨與船體的焊接處和船體表面的腐蝕缺陷處等都會產生應力集中[15-17]，另外，潛艇在下潛與上浮的過程中，結構應力會隨著靜水壓力的變化而發生顯著的改變[18]. 載荷和腐蝕介質的交互作用被定義為金屬腐蝕的力學化學效應，它主要包括在載荷和腐蝕介質的協同作用下金屬腐蝕電位的降低和腐蝕速率的增大[19-20]. 已有研究[21]表明，在結構應力接近160 MPa時，Q235B鋼在質量分數為3.5%的NaCl溶液中的腐蝕速率增大了約44%，因此，金屬在海水中腐蝕的力學化學效應不容忽視. 然而，這些研究并沒有考慮力學因素對腐蝕電場的影響，而載荷與腐蝕介質協同作用下的腐蝕電場的研究具有重要的工程意義和實用價值，因此，本文旨在研究艦船在服役過程中產生的復雜應力應變對其腐蝕電場的影響規律.

隨著服役時間的增加，船殼的防腐涂層不可避免地會遭到破損，涂層破損處發生嚴重的腐蝕而形成腐蝕缺陷，在外界作用力下，腐蝕缺陷處會產生應力集中. 因此，本文基于腐蝕缺陷，將結構應力應變耦合到電極反應的平衡電位和交換電流密度表達式以建立腐蝕電場的力學化學耦合模型，得到了拉伸位移對力學化學耦合效應下腐蝕電位、電流密度以及腐蝕電場的影響規律.

1 數值仿真模型

采用COMSOL Multiphysics仿真軟件建立基于腐蝕缺陷的力學化學耦合模型，仿真模型主要分析以下3個方面內容：一是船體鋼的彈塑性固體應力分布；二是在固體應力和腐蝕介質協同作用下溶液中的電位分布以及金屬/溶液界面的腐蝕電位分布；三是在力學化學效應下溶液中的腐蝕電場分布，前者采用固體力學模塊求解，后兩者采用二次電流分布模塊求解.

1.1 結構應力仿真

由于圓柱殼體的對稱性，將船體結構的三維模型簡化為二維模型，如圖1所示，取船體鋼的長度為兩肋骨間的單跨長度(0.6 m)，殼體厚度為28 mm，腐蝕缺陷為橢球型，其長度為200 mm，深度為12 mm. 考慮到船體結構腐蝕缺陷處的應力集中可能會導致局部的塑性變形，因此，使用小塑性應變模型和von Mises屈服準則來實現船體結構的彈塑性應力仿真，并采用各向同性硬化模型，相應的硬化函數(σyhard)定義[20]為

σyhard=σexp(εeff)-σys=σexp(εp+σe/E)-σys.

(1)

式中：σexp為由船體鋼應力應變曲線得到的實驗應力函數，εeff為彈塑性應變，σys為船體鋼的屈服強度，εp為塑性應變，σe為彈性應力，E為彈性模量，σe/E為彈性應變.

圖1 基于腐蝕缺陷的力學化學耦合模型示意圖

由拉伸實驗得到船體鋼的應力-應變曲線如圖2所示，采用控制位移的方式對試樣進行加載，加載速度為1 mm/min，拉伸過程中并沒有出現明顯的屈服現象，故取塑性應變為0.2%所對應的應力值為船體鋼的屈服強度，因此，船體鋼的屈服強度和抗拉強度分別為708、754 MPa，彈性模量為200 GPa，泊松比為0.3. 邊界條件：考慮到船體結構的受力較為復雜，將船體鋼右端簡化為沿X方向的拉伸位移d，在Y方向為自由移動，利用COMSOL軟件中參數化掃描功能實現拉伸位移的變化，位移取值分別為0、0.4、0.8、1.2、1.6、1.8 mm；船體鋼的左端為固定約束；船體鋼的內壁在Y方向的位移為0，在X方向為自由移動. 網格類型為自由三角形網格，且在腐蝕缺陷處進行了細分處理，最大和最小單元尺寸分別為2.00、0.18 mm，三角形單元總數為22 538個.

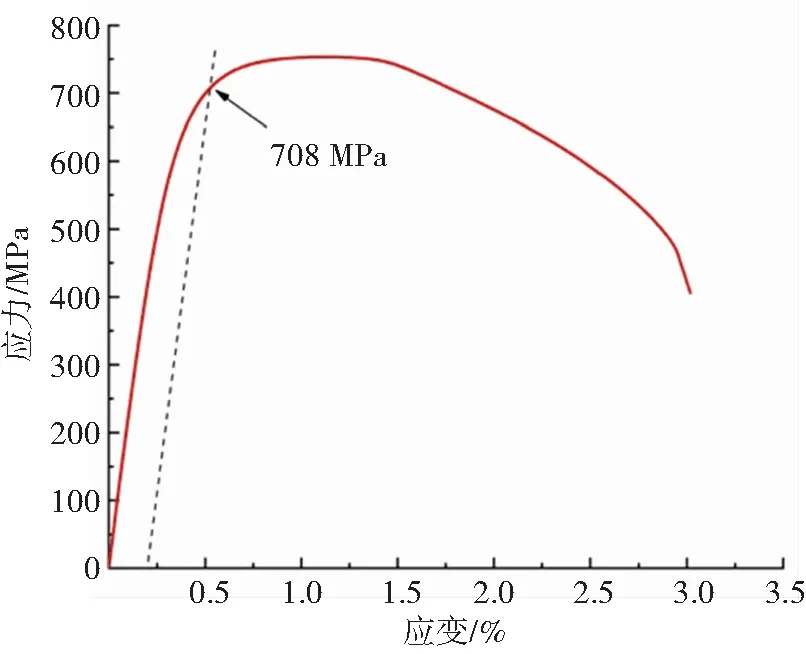
圖2 船體鋼應力應變曲線

1.2 力學化學耦合模型

考慮到實際情況，對模型進行以下假設：1)船體鋼的主要成分為鐵，故認為陽極溶解反應只有鐵的氧化反應而忽略其他雜質元素的溶解；2)船體鋼在自腐蝕電位下，氧還原和鐵氧化反應均屬于高過電位下的電極反應，因此，電極過程動力學由Butler-Volmer方程簡化為Tafel方程；3)鋼/溶液界面同時發生鐵的氧化與氧的還原兩個共軛反應，而溶液的其他邊界為電絕緣.

鐵陽極氧化溶解的局部電流為

(2)

ηa=φ-φa,eq，

(3)

其中φ為鋼/溶液界面的電極電位，φa,eq為應力狀態下陽極反應的平衡電位，并由下式[15]計算

(4)

(5)

(6)

研究表明，應力的存在會加速陰極反應的交換電流密度，描述力學化學效應對陰極反應交換電流密度影響的半經驗公式[20]為

(7)

采用三電極體系在CS310電化學工作站上測試船體鋼的動電位極化曲線，實驗介質為質量分數為3.5%的NaCl溶液. 工作電極為采用環氧樹脂封裝的圓柱形船體鋼，其直徑為1.1 cm，高度為1 cm，金屬暴露面積為1 cm2，用SiC濕砂紙逐級打磨至1 000目，丙酮脫脂，并依次用乙醇和蒸餾水沖洗，然后置于干燥箱中烘干；參比電極為Ag/AgCl電極；輔助電極為鉑片電極. 工作電極先在待測溶液中浸泡一段時間，等到開路電位基本穩定后開始測試，極化曲線的掃描電位為-1.1～-0.1 V(相對參比電極)，掃描速率為1.0 mV/s. 圖3為船體鋼在質量分數為3.5%的NaCl溶液中的極化曲線，由極化曲線得到船體鋼的腐蝕電化學參數見表1.

圖3 船體鋼在質量分數為3.5%的NaCl溶液中的極化曲線

表1 船體鋼的腐蝕電化學參數

1.3 溶液中的電場分布

對于二維腐蝕電場問題，電極/溶液界面的電極電位和溶液中的電位分布符合拉普拉斯方程[8]：

(8)

根據電場與電位的關系式E=-φ，則

(9)

式中：EX、EY分別為溶液中電場的X和Y分量，|E|為電場模量.

2 結果與討論

2.1 腐蝕缺陷處的應力分布

圖4為由力學化學耦合模型計算得到的不同拉伸位移下腐蝕缺陷處的von Mises應力分布，由圖可知，應力對稱分布于腐蝕缺陷中心兩側，且最大應力出現在腐蝕缺陷中心，而腐蝕缺陷的兩端點則出現應力最小值. 結構的von Mises應力水平隨著拉伸位移的增大而增大，當拉伸位移為1.6 mm和1.8 mm時，腐蝕缺陷中心區域的局部應力值超過了船體鋼的屈服強度(708 MPa)，此時，腐蝕缺陷中心區域發生了一定程度的塑性變形，而其他區域則仍處于彈性應力階段.

圖4 不同拉伸位移下腐蝕缺陷處的應力分布

2.2 力學化學效應對腐蝕電位的影響

圖5為不同拉伸位移下溶液中的電位分布和船體鋼中的應力分布，由圖可知，船體鋼中的腐蝕缺陷處發生了明顯的應力集中，且拉伸位移越大應力集中效應也越明顯，缺陷的其他區域的應力分布則較為均勻. 溶液中的電位隨著拉伸位移的增大而負移，由于船體鋼中腐蝕缺陷處的應力集中，導致了溶液中電位分布的不均勻性，且拉伸位移越大，溶液中電位分布的不均勻性越明顯. 當拉伸位移為1.6 mm和1.8 mm時，腐蝕缺陷附近的溶液與其他區域的溶液形成了明顯的電位差，這與2.1節中分析的腐蝕缺陷中心區域發生的塑性變形有關.

圖5 不同拉伸位移下溶液中的電位分布和船體鋼中的應力分布

圖6為由力學化學耦合模型計算得到的不同拉伸位移下金屬/溶液界面的腐蝕電位分布，當拉伸位移為0 mm時，電極表面的腐蝕電位處處相等，當拉伸位移不為零時，缺陷兩邊的腐蝕電位隨著拉伸位移的增大均勻地負移，而缺陷處腐蝕電位的負移量大于兩邊，尤其是拉伸位移為1.6 mm和1.8 mm時，缺陷中心區域的腐蝕電位負移量遠遠大于兩邊，這是因為此時缺陷中心區域發生了塑性變形. 根據電化學理論推導，可得由于應力引起的金屬腐蝕電位的變化值[21]為

(10)

式中Δφa,eq為力學化學效應所引起的陽極氧化反應平衡電位的負移量，即

(11)

圖6 不同拉伸位移下金屬/溶液界面的腐蝕電位分布

由式(10)、(11)可知，當金屬結構不發生塑性變形(εp=0)時，由于力學化學效應引起的金屬腐蝕電位的負移量與Von Mises應力存在線性關系，當結構發生塑性變形時，式(11)中的ΔP為屈服強度，且腐蝕電位負移量與塑性應變之間存在對數關系，因此，腐蝕電位負移量明顯增大，文獻[22]也證實了彈塑性應變所引起的力學化學效應明顯大于彈性應力. 在彈性變形范圍內，當原子由晶格節點的平衡位置做較小的位移時，受激的金屬原子將增加其位能，該位能使受激的金屬原子的電化學位增加，電化學位的改變將引起平衡電位的改變. 金屬在塑性變形范圍內，產生新的位錯并形成位錯平面塞積群，從而引起電化學位的增大，在塑性滑移條件下，單位體積內完成的機械變形功等于系統在單位體積中形成位錯時熱力勢的增加，由此可以得到位錯密度與因位錯產生的電化學位之間的關系. 因此，不論是彈性變形還是塑性變形都會導致金屬的電化學電位增大，從而使得金屬的平衡電位降低，由式(10)可知，金屬的腐蝕電位相應降低.

2.3 力學化學效應對電流密度及腐蝕電場的影響

圖7為由力學化學耦合模型計算得到的不同拉伸位移下腐蝕缺陷處的陰陽極電流密度分布以及凈電流密度分布. 當拉伸位移為0 mm時，船體鋼表面的鐵陽極氧化溶解反應電流密度處處相等，都為85 mA/m2，當拉伸位移從0.4 mm增大到1.2 mm時，鐵陽極氧化電流密度也隨之增大，且電流密度在整個腐蝕缺陷的長度上分布較為均勻，當拉伸位移進一步增大到1.6 mm和1.8 mm時，腐蝕缺陷中心的陽極氧化電流密度急劇增大，分別為130 mA/m2和142 mA/m2，由于腐蝕缺陷兩端點的應力值最小，因此，這兩點的陽極氧化電流密度也最小. 當不存在拉伸位移時，船體鋼表面的氧陰極還原的電流密度都為-85 mA/m2，這與陽極氧化電流密度的大小相等，陰極電流密度大小隨著拉伸位移的增大而增大，塑性變形對陰極還原反應力學化學效應的影響也大于彈性變形. 當腐蝕缺陷處發生彈性變形時，缺陷長度上的凈電流密度均小于5 mA/m2，而發生塑性變形時，缺陷中心的凈電流密度急劇增大，分別為21、28 mA/m2，而缺陷兩邊的凈電流密度為負，說明由于缺陷附近應力分布的不均勻引起了局部的應力腐蝕電偶.

圖8為不同拉伸位移下溶液中的腐蝕電場模量和船體鋼中的應力分布，圖中箭頭方向為溶液中的電流流向，箭頭大小正比于電流大小. 由圖可知，隨著拉伸位移的增大，腐蝕缺陷處的應力增大，導致溶液中的腐蝕電場明顯增大，且電流由腐蝕缺陷中心流向兩邊，這是因為缺陷中心的應力集中使得溶液中的電位負移，溶液中電位梯度的存在為溶液中的電流流動提供了驅動力，從而形成應力腐蝕電偶，且缺陷中心為陽極而缺陷兩邊為陰極. 另外，腐蝕缺陷的面積遠遠小于非缺陷區域，形成了小陽極大陰極的現象，這使得應力腐蝕電偶效應進一步增強，因此產生的腐蝕電場也越大.

(a)陽極電流密度

(b)陰極電流密度

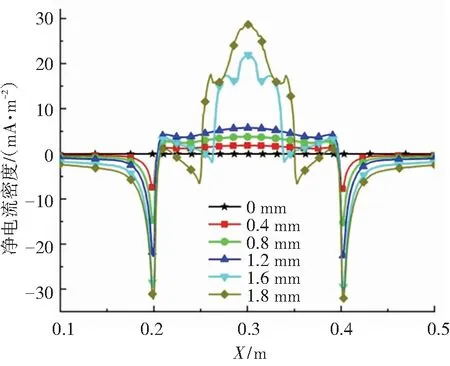
(c)凈電流密度

圖9為由力學化學耦合模型計算得到的不同拉伸位移下腐蝕缺陷處的電場模量分布，當拉伸位移為零時，船體鋼不存在應力，其表面發生均勻腐蝕，陽極電流密度與陰極電流密度大小相等符號相反，因此不產生腐蝕電場. 當拉伸位移不為零時，腐蝕缺陷處的應力集中導致了應力腐蝕電偶的形成，從而產生腐蝕電場，彈性變形范圍內，腐蝕電場在缺陷長度上均勻分布，電場模量隨著應力的增大而均勻增大，且電場模量值均較小，發生塑性變形時，腐蝕電場顯著增大，這是因為金屬在塑性變形的易滑移階段和形變強化階段產生新的位錯并形成位錯平面塞積群，導致力學化學效應急劇增大[23].

圖8 不同拉伸位移下溶液中的腐蝕電場模量分布

圖9 不同拉伸位移下腐蝕缺陷處的電場模量分布

3 結 論

1) 應力對稱分布于腐蝕缺陷中心兩側，缺陷中心存在應力集中，當拉伸位移為1.6 mm和1.8 mm時，缺陷中心區域發生了一定程度的塑性變形.

2)力學化學效應使得金屬腐蝕電位負移，缺陷處的應力集中導致了溶液中電位分布的不均勻性，當發生塑性變形時，腐蝕缺陷附近的溶液與其他區域的溶液形成了明顯的電位差.

3)溶液中電位梯度的存在為電流流動提供了驅動力，從而形成應力腐蝕電偶，且缺陷中心為陽極而缺陷兩邊為陰極，由于腐蝕缺陷的面積遠遠小于非缺陷區域，因此形成了小陽極大陰極的現象，這使得應力腐蝕電偶效應進一步增強.

4)塑性范圍內的力學化學效應明顯大于彈性階段.