指向提升學力的“問題鏈”教學策略

孟凡亮

[摘 ?要] “問題鏈”可以觸動教學目標，可以激活教學過程，基于“問題鏈”的教學設計是生動的，也是具有魅力的. 文章首先對“問題鏈”進行解讀，進而展示了“垂直平分線性質(zhì)的逆定理”一課的教學設計. 該教學設計以問題鏈的形式呈現(xiàn)，提出對準教學目標設計問題和以問題驅(qū)動為設計理念的教學策略.

[關鍵詞] 問題鏈;學習能力;策略

問題是思維的動力，更是數(shù)學的靈魂，離開了問題的數(shù)學課堂是失去靈氣的，沒有問題的數(shù)學課堂無法激活學生思維. 可見，問題是提升數(shù)學課堂效率和發(fā)展學生思維能力的關鍵所在. 初中數(shù)學對學生抽象思維的要求較高，很多時候有待解決的問題具有較大的難度或具有較強的靈活性，此時需要教師設計一連串的問題來啟智導學，這樣的一連串的問題就是“問題鏈”. “問題鏈”作為一種常見的問題設計方式，在初中數(shù)學教學中意義重大，可以激發(fā)學趣，可以引導學生進行積極的思維活動，可以有效化解教學重難點，可以訓練并發(fā)展思維，可以促進學生自主構建，可以提高學生的數(shù)學學習能力.

“問題鏈”的解讀

那么，什么是“問題鏈”？筆者認為，“問題鏈”是問題結(jié)構的表現(xiàn)形式之一，通常就是基于數(shù)學本質(zhì)，對原問題進行特殊化處理，將其分為層層深入的多個小問題，這多個小問題之間具有隱性的內(nèi)在聯(lián)系卻又相對獨立，通常前一個問題是后一個問題的鋪墊，后一個問題是前一個的遞進，就這樣，將新知學習轉(zhuǎn)化為解決一系列問題，讓學生在一步步的問題解決中，自然地進行新知的攝取和能力的攀登，以實現(xiàn)自主建構，完善數(shù)學的知識體系.

“問題鏈”教學策略案例

既然“問題鏈”教學可以引導學生主動思考、自主探究和自主建構，那么該如何將其落實于具體的教學實踐中去？本文，筆者在深鉆教材和深入了解學情的基礎之上，以“垂直平分線性質(zhì)的逆定理”的課堂教學為例，談談教學中如何以“問題鏈”為導向去揭示數(shù)學概念的形成過程和數(shù)學知識的內(nèi)在關聯(lián)，讓學生經(jīng)歷“思考—探究—發(fā)現(xiàn)—反思”的思維過程，提高學習能力.

1. 溫故知新——指向?qū)W生經(jīng)驗，引發(fā)思考

問題1：一起回憶一下，上節(jié)課我們學習了什么？請試著用幾何語言進行表達.

問題2：誰能說出垂直平分線性質(zhì)的逆命題？這是一個真命題嗎？

設計意圖 ?溫故而知新，這里將“問題鏈”作為教學的起點，教師的問題設計具有一定的指向性. 教師探尋到學生學習心理與問題的聯(lián)系，問題1以回憶舊知來引入新課，可以充分調(diào)動學生的知識儲備，讓學生去動手操作和積極思考，為問題2的解決奠基. 問題2的提出則是為了指導學生展開合情猜想，并適時引出課題，培養(yǎng)學生的逆向思維.

2. 數(shù)學探究——指向探究過程，獲得建構

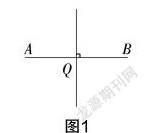
問題3：請找出圖1中到線段AB兩端距離相等的點.

問題4：請利用圓規(guī)在圖2中找出一點Q，使得QA=QB，并說一說你作圖的方法.

問題5：利用圓規(guī)在圖2中再找出一點E，使得EA=EB. 請畫出直線QE，并說一說線段AB和直線QE有何關系.

問題6：諸如點E的點有幾個？這些點都在哪個位置？

問題7：如圖1，試證明到線段AB兩端距離相等的點都在其垂直平分線上.

問題8：試著畫出線段AB的垂直平分線.

設計意圖 ?問題鏈的呈現(xiàn)將完整地再現(xiàn)知識的發(fā)生和發(fā)展歷程，讓數(shù)學知識的價值得以最大化，使得數(shù)學課堂變得生動而流暢. 本環(huán)節(jié)中，教師首先讓學生自我嘗試著去解決問題，學生經(jīng)過思考易想到利用刻度尺進行探究的策略;接著，讓學生進行動手操作，在反復嘗試的過程中獲得更一般的方法，以滲透從特殊到一般的數(shù)學思想;然后，鼓勵學生進行猜想，并獲得發(fā)現(xiàn)“這樣的點有無數(shù)個，且位于線段AB的垂直平分線上”，這樣的感覺僅僅是學生的猜想，顯然需要進一步進行驗證;之后，引領學生討論和歸納得出逆定理，并作圖以符號語言表示;整個探究過程中，問題7是教學的重難點，要知道任何定理的得出都需要經(jīng)歷嚴密的推理，那么下一步自然是進行推理驗證，此處應引導學生分成兩種情況討論，即在線段AB上和在線段AB外，借機滲透分類討論的數(shù)學思想，并培養(yǎng)演繹推理能力;最后，通過作圖，讓學生回憶作圖經(jīng)歷，總結(jié)作圖步驟，深化認識.

3. 應用提升——指向應用與拓展的深加工

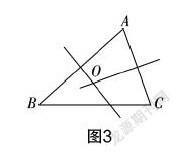
問題9：已知△ABC，在圖3中分別作出邊AB與AC的垂直平分線l和l，且l與l交于點O，那么點O是否在邊BC的垂直平分線上？請予以作圖觀察.

問題10：請試著證明點O也在邊BC的垂直平分線上.

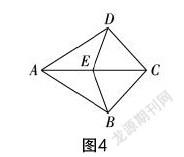
問題11：請試著用盡可能多的方法解決以下問題：如圖4，已知AB=AD，BC=DC，且點E在AC上，證明：EB=ED.

設計意圖 ?以問題9為載體，為學生打造鞏固作垂直平分線方法的要素，同時鼓勵學生直觀猜想結(jié)論，為進一步證明奠基;問題10則再一次從合情推理向著演繹推理邁進，讓學生在證明中獲取認識. 最后拋出一道應用問題，不少學生拿到題目立刻想到用全等知識進行證明，此處筆者提出用多種方法解決的要求，就是為學生嘗試利用新知來解題提供動力，讓學生體會創(chuàng)新解法的簡潔性和靈活性，同時有助于學生實現(xiàn)自我突破，發(fā)展邏輯推理素養(yǎng).

4. 課堂小結(jié)——指向?qū)W力提升和思想感悟

問題12：通過今天學習，你收獲了什么？

設計意圖 ?以問題為驅(qū)動，讓學生在回憶中感悟知識間螺旋上升的關系，感悟數(shù)形結(jié)合、分類討論及符號化數(shù)學思想是數(shù)學教學的精髓，在基于“問題鏈”教學的過程中不斷浸潤，發(fā)展空間觀念和演繹推理能力，最終提高學生的學習能力. 此處，學生由于認知水平、學習經(jīng)驗和學習能力等方面的差異對本節(jié)課會有不同的感悟.

基于課例的幾點思考

問題作為課堂教學的一個重要支點，承載著激趣引思、啟迪思維和質(zhì)疑問難等重要作用，從現(xiàn)代理論所倡導的“問題鏈”教學模式不難看出，問題設計是教學的必要環(huán)節(jié)，是課堂教學的驅(qū)動所在，在數(shù)學教學中設計“問題鏈”，筆者認為有如下策略：

1. 對準教學目標設計問題

教學目標是教學過程所需達成的結(jié)果，也是展開課堂教學的總綱. 傳統(tǒng)教學中，我們所設計的教學目標往往籠統(tǒng)而寬泛，這樣的教學缺乏目的性，從而使得教學缺乏實效性. 從而，教師應在課堂做好充足準備，所設計的問題要對準教學目標，這樣才能徹底摒棄傳統(tǒng)教學的目標過于寬泛的情形. 本節(jié)課中，教師基于教材與學情準確定位教學目標和重難點，立意時做了雙重考慮，一方面，通過解決問題鏈中的系列問題來突破本課的重難點“證明到一線段兩端距離相等的點在該線段的垂直平分線上”，這是對逆定理深化理解的一個必要步驟，是學生繼續(xù)建構的過程. 另一方面，通過問題鏈的指引，不僅完成了重難點的突破，更是有效滲透了多個數(shù)學思想方法.

2. 以問題驅(qū)動為設計理念

問題鏈的序列性有效克服了傳統(tǒng)教學中提問的細碎、零散和隨意，讓學生在解決問題鏈的過程中習得知識、獲得解決問題的策略及提高學習能力. 本課中，教師僅僅是提供了問題鏈，并在學生問題解決中及時、適時做出評價，問題解決的主動權在于學生，歸納提煉的工作也是在師生交流中完成的，并在主動參與和積極討論中將每個學生的觀點納入課堂. 由于在解決問題中獲得的方法，深化了學生的理解，更重要的是轉(zhuǎn)化成了學習能力，以便在之后的學習中有效提取.

總之，指向提升學力的問題串設計并非易事，在實施“問題鏈”教學的過程中，教師需要深入鉆研教材和學生，所設計的問題要對準教學目標，突出教學重難點，需問于學生有疑問的地方，促進其對問題的理解. 更重要的是以問題驅(qū)動為設計理念，引領學生積極思考，在主動參與和積極討論中將每個學生的觀點納入課堂，只有這樣，才能讓數(shù)學課堂更具活力，從而有效提高學生的學習能力.

3033501908208