借助幾何直觀促進學生數(shù)學知識建構(gòu)

付文英

《義務教育數(shù)學課程標準（2011版）》指出：“幾何直觀可以幫助學生直觀地理解數(shù)學，在整個數(shù)學學習過程中都發(fā)揮著重要作用。”直觀模型作為建立幾何直觀的重要載體，在教學中發(fā)揮著不可忽視的作用。近年來，筆者在課堂教學中不斷探索，借助圖形或?qū)嵨锏戎庇^模型，引導學生直觀地進行數(shù)學的思考和想象，幫助學生經(jīng)歷和感受建模過程，體會模型思想。

一、借助直觀模型，建立等量關(guān)系

實物模型以其直觀的形式容易為人們所接受，給人們帶來無窮無盡的直觀源泉，也為研究數(shù)學和解決問題提供了工具。尤其是小學生以形象思維為主，借助實物模型更加有利于他們對知識的理解和掌握。教學中可以借助實物模型，使學生在觀察與操作中明晰數(shù)量間的關(guān)系。

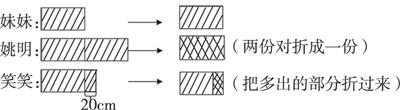
如教學北師大版《數(shù)學》四年級下冊“等量關(guān)系”這一課時，由于數(shù)學知識較為抽象，學習基礎(chǔ)又相對欠缺，學生受以前學習經(jīng)驗的影響，習慣了看信息后列式計算，對等量關(guān)系式這種陌生的表示方法不習慣，也不易理解。為了讓學生明確姚明、笑笑、妹妹三者之間的身高關(guān)系，筆者還設(shè)計了三個長方形紙條，借助紙條進行演示：以妹妹身高為標準，其他兩個量以“折疊-對比-展開”的方式進行動態(tài)演示。通過直觀操作，學生不僅直觀地感受到兩個量之間的倍數(shù)關(guān)系或相差關(guān)系，建立了等量關(guān)系，寫出了兩個量之間的等量關(guān)系式，而且進一步理解了每一個等量關(guān)系式的具體意義，有效地突破了教學的重難點（如圖1）。

在上述演示過程中，不僅清楚地看出“姚明的身高是妹妹的2倍，笑笑身高比妹妹多20厘米”，而且還架起了姚明身高與笑笑身高之間關(guān)系的橋梁，即“姚明身高÷2”和“笑笑身高-20厘米”都可以表示妹妹的身高，所以學生就直觀地理解了“姚明身高÷2=笑笑身高-20厘米”“ 姚明身高÷2+20厘米=笑笑身高”“（笑笑身高-20厘米）×2=姚明身高”這一系列的等量關(guān)系式。幾個簡單的比劃動作，勝過千言萬語，一系列等量關(guān)系式的由來及意義盡收眼底。三張小紙條，發(fā)揮了大作用。

二、借助直觀模型，理解算理算法

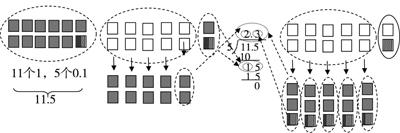
在計算教學中，算理的理解是教學中的一大難點，借助直觀的模型操作可以幫助學生明白每一步計算的意思、每一個數(shù)字的由來及書寫位置確定的根據(jù)，使學生在理解的基礎(chǔ)上更好地掌握算法，從而提高計算能力。如教學北師大版《數(shù)學》四年級下冊“小數(shù)除以整數(shù)”一課時，在運用“元、角、分”的生活經(jīng)驗解決“11.5÷5”這一問題以后，為了讓學生更深入地從數(shù)值的角度理解計算過程，筆者借助課件演示分圖形的活動，利用“數(shù)形結(jié)合”的方法，結(jié)合活動過程，使學生進一步體會小數(shù)除法也是“平均分”這一本質(zhì)意義。結(jié)合分圖形活動的每一步，引導學生觀察、思考、發(fā)現(xiàn)并建立數(shù)學符號與操作活動的聯(lián)系，理解直觀操作與豎式間的一一對應關(guān)系。結(jié)合圖形的動態(tài)演示，使學生明白：豎式只不過是把平均分的操作活動用數(shù)學符號記錄下來的一種形式。讓學生經(jīng)歷將操作活動抽象為豎式的數(shù)學

化過程，體會豎式中每一步的合理性，從而達到借助直觀模型理解小數(shù)除以整數(shù)的算理，實現(xiàn)算理直觀（如圖2）。

三、借助直觀模型，探索數(shù)學規(guī)律

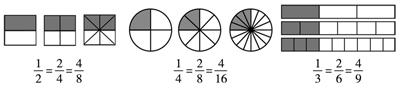
很多數(shù)學知識具有雙重性，既具有數(shù)的特征，又具有形的特征，實際教學中，可以借助直觀模型把兩個方面結(jié)合起來，幫助我們發(fā)現(xiàn)并掌握其本質(zhì)意義以及內(nèi)在的規(guī)律。如在教學北師大版《數(shù)學》五年級上冊“分數(shù)基本性質(zhì)”這一課時，為了引導學生探索并發(fā)現(xiàn)分數(shù)的基本性質(zhì)這一規(guī)律性知識，筆者借助折紙活動，把靜態(tài)的知識變?yōu)閯討B(tài)的操作活動，使學生在動態(tài)的探索過程中發(fā)現(xiàn)不同分數(shù)之間分子、分母的變化規(guī)律。第一個層次，由數(shù)到形，給出一組三個分數(shù)，并根據(jù)分數(shù)大小進行涂色，學生在涂色后通過觀察圖形中涂色部分的面積是一樣的，發(fā)現(xiàn)三個分數(shù)大小是相等的。第二個層次，由形到數(shù)，每人準備三張形狀大小相同的紙片，通過自己動手折紙創(chuàng)造出一組大小相等的分數(shù)，通過觀察和比較，再次發(fā)現(xiàn)每組圖形涂色面積一樣，因此三個分數(shù)大小也一樣。最后通過紙條間的份數(shù)對比，發(fā)現(xiàn)涂色部分份數(shù)擴大的倍數(shù)與總份數(shù)擴大的倍數(shù)是一致的。這樣的設(shè)計，運用數(shù)形結(jié)合，為學生建構(gòu)知識搭起了橋梁，為探索分子分母之間的變化規(guī)律提供了必要的素材及理解上的直觀支撐（如圖3）。

四、借助直觀模型，理解概念內(nèi)涵

數(shù)學知識的抽象性，使以形象思維為主的小學生學習起來有一定難度，特別是對一些概念性知識理解起來困難更大。教學過程中可以借助直觀實物模型，在動態(tài)的操作變化中幫助學生理解概念的本質(zhì)意義。如，教學北師大版《數(shù)學》四年級下冊“平均數(shù)”一課時，教學的難點是對“平均數(shù)”意義的理解。雖然學生可以通過計算得出結(jié)果，但對“平均數(shù)表示一組數(shù)據(jù)的平均水平”這一本質(zhì)意義的認識和理解的深度還不夠。為了讓學生理解這個數(shù)的由來及其意義直觀展示出來的狀態(tài)，教學中，可以借助直觀實物模型幫助學生理解概念的本質(zhì)所在。在創(chuàng)設(shè)情境收集出一組數(shù)據(jù)后，用直觀的象形統(tǒng)計圖表示出來。在分析這組數(shù)據(jù)“哪個數(shù)可以代表小明的投籃水平”的過程中，借助“移多補少”的操作活動，讓學生明確平均數(shù)的由來;借助“水平線”的產(chǎn)生，讓學生清楚平均數(shù)代表一組數(shù)據(jù)平均水平的科學性。在用直觀的實物模型的操作過程中，學生共同經(jīng)歷了探尋平均數(shù)的過程，而且理解了平均數(shù)的意義，較好地突破了教學難點（如圖4）。

五、借助直觀模型，促進數(shù)感發(fā)展

數(shù)感在小學數(shù)學教學中有著非常重要的作用。借助直觀模型可以促進學生數(shù)感的發(fā)展，力圖從表象到實質(zhì)，實現(xiàn)數(shù)感的有效建立。如教學北師大版《數(shù)學》四年級下冊“小數(shù)的大小比較”一課時，為比較2.97，3.13，3.08這三個小數(shù)的大小，除了從小數(shù)的意義和化成低級單位比較外，為了便于學生直觀感知三個數(shù)的大小，可以利用知識的遷移，借助數(shù)位順序表，從位值的角度比較，得出多個小數(shù)大小比較的方法。還可以借助數(shù)線圖，利用數(shù)與數(shù)軸上點的一一對應關(guān)系，呈現(xiàn)這三個小數(shù)的前后位置，從它們在數(shù)軸上所在的位置直觀發(fā)現(xiàn)并理解三個小數(shù)的大小，感受數(shù)的大小關(guān)系與點的位置關(guān)系之間的密切相聯(lián)。

幾何直觀是一種思維方式，在課堂上我們充分借助直觀模型，讓學生對幾何直觀多一些感性的體驗，讓學生的不同思維方式有機共存、相互補充，以凸顯數(shù)學本質(zhì)，促進知識構(gòu)建，提升高效課堂。

[責任編輯：陳國慶]