高中數學教學效率的案例研究

[摘 ?要] 文章通過對2019年高一新生在人教A版必修1函數模塊的入門教學的案例研究，發現學生個體和班級整體對數學題型學習與發展的規律及教學效率的影響因素，并根據案例分析和教學經驗提出了高效的高中數學教學的基本原則和策略.

[關鍵詞] 高中;數學教學;效率

研究背景

從20世紀80年代以來，我們進行了一系列的數學教學改革，但大多數都銷聲匿跡了，其中最致命的原因是缺乏效率意識. 這告訴我們，改革者有無效率意識，改革方案能否實施高效的數學教學，乃是一項硬指標，是具有否決權的“一票”[1]. 國內有關數學教學的效率和有效性的研究文獻很多，說明對這個問題的關注度高，但縱觀國內外關于數學教學效率的研究，尚存在以下問題或不足：（1）脫離具體的教學內容和教學目標而空談效率;（2）缺乏課堂教學后學生實際學習效果的跟蹤調查研究，教學效果如何是由學生的學習成果來決定的. 文章就是對自然教學情境中高中數學教與學案例進行的跟蹤調查研究.

研究方法

1. 采取行動研究法，質性和量化分析結合

由于教育的高度復雜性，嚴格控制的對比實驗研究在學校難以進行，所以在自然、真實的教育環境中進行“行動研究”就成了可行和必要的方法. 籠統的教育量化分析可以看到外部的整體特征，但難以洞察到復雜的教學現象的內在本質，所以教育研究要將質性和量化結合. 案例分析對發現教育的問題和本質是不可或缺的，有道是“一個好的案例，勝過一千次說教”.

2. 研究對象和過程

研究對象主要是2019年9月新入學的筆者任教的高一（13）班的學生. 這所福建省一級重點高中每年高考的一本上線率在35%左右，本科上線率在90%左右. 這個普通平行班（共50人）預計能達到一本上線十幾人的水平. 重點是調查研究高一上學期期中考試前2個月的教與學的情況，此時正是高一新生的數學入門學習階段，學習的內容又是比較抽象、難學的人教A版必修一的函數，學生的學習困難很多，易于發現問題. 筆者對（13）班學生使用了自己設計的數學作業和相應的教學方法，用作對比的是采取傳統的教學方式和教輔作業的另一筆者任教的（11）班和其他平行班，年段有2～14共13個平行班.

研究結果與分析

1. 案例1：復合函數的單調性問題

（1）課后作業訓練的變式進程——分析復合函數的單調性：第一次，f（x）=;第二次，f（x）=;第三次，y=;第四次，y=;第五次，y=;第六次，f（x）=log（1-x2）;第七次，f（x）=lg（3-2x-x2）.

（2）高一（13）班整體教與學的進程及分析：

第一次（9月12日），課堂上教師講析一個范例后，學生做了一個匹配練習題（沒有板演）;教師再講析，此題作為課后作業的正確率是34%.

教學反思：教師認為這種題型的解法步驟簡單明確，講解也很清晰，出現這么差的教學效果真是出乎意料. 經過深入的訪談等調查分析，發現主要原因是高一新生難以理解這種初中沒有學過的形式化的抽象代數推理. 不理解的內容易忘記，也無法自己推求，晚自習做匹配練習時就記憶模糊、混亂，無所適從了.

第二次（9月17日），課堂上對前函數的單調性和奇偶性進行階段性復習，并匹配相應的課后作業，此題屬于作業中的“錯題再練”，結果是54%的正確率，進步顯著.

第三次（9月21日），此題作為最后的“預習探究”作業，結果只有12%的正確率. 可見高一新生應對較新的變式問題時處理能力很差，在此入門階段的學習，多數學生還是處于模仿的學習狀態.

第四次（9月23日），在上課的最后講析了此類范例，但因時間不足，沒有當堂匹配練習，結果是此題作為課后作業只有26%的正確率，教學效果很差.

第五次（9月24日），此題作為課堂上講評后的課后作業之“錯題再練”，結果是82%的正確率，進步顯著.

第六次（9月28日），課堂上講析了范例，此題作為課后作業是70%的正確率，說明（13）班大多數學生對此類題型的掌握漸入佳境.

第七次（10月30日），作為當天下午第二節的課堂測試，此題的結果居然是只有34%的正確率. 進一步對學生的訪談發現，不會做或做錯的主要原因是淡忘了教師教的此類題型的解法. 經過教師的提示，學生回想起來之后，多數學生又能解答出來了.

（3）代表性的學生個案學習進程與分析.

①數學成績是班級的后10名，悟性較差，但學習認真的女生吳：第一次的作業正確，第二次的作業錯誤，第三次、第四次、第五次的作業都正確，第六次、第七次的作業又錯誤了. 調查和訪談發現，此女生因學習認真，課堂筆記做得較清楚，即使不怎么理解，也可以通過逐步模仿正確解答，但間隔時間一長就容易因為淡忘而不會做或做錯.

②數學成績在班級10名至20名之間，悟性較好，但作業馬虎的男生林：第一次、第二次、第三次、第四次、第五次、第六次的作業都錯了，第七次測試過程雖不規范，但結論正確. 錯因主要是其不按照教師示例的三步去推求，訂正也不認真，總是習慣于隨心亂寫，思維不嚴謹.

③數學成績在班級前10名的優秀男生黃：除了在第四次的作業因“跳步”、太匆忙而發生了錯誤外，其他幾次作業全部正確. 這樣多次的重復訓練對此水平的優秀學生有些不必要了.

教學反思：對比女生吳和男生林的學習過程發現，嚴格落實學生規范解答的要求對促進學生掌握數學和提高教學效率具有必要性. 因為數學是研究模式的科學，大多數常規題型的基本解題過程都可以“算法化”分步操作，這樣易于學生先學會模仿操作和減少錯誤，然后在操作中逐步理解，而且規范化操作有利于促進學生快速準確地解答基本題型.

案例分析后發現，雖然學生的最后答案是在正確與錯誤之間擺動，但在總體上其理解和掌握是對錯誤的反思糾正而前進的.

2. 案例2：分段的奇函數問題

（1）課后作業訓練的變式進程：第一次，作業為“設f（x）是定義在R上的奇函數，已知當x≤0時，f（x）=2x2-x，求f（x）的解析式”;后繼的變式作業只是對“已知”做了諸如“當x>0時，f（x）=lgx+x-1”等方式的改變，其他不變（詳略）.

（2）高一（13）班整體教與學的進程及分析：

第一次（9月14日），課堂上講析了此類范例，但沒有時間做匹配練習，課后此題作為作業只有34%的正確率.

第二次（9月16日），在前14日“講練評”一輪后，課后此題作為作業仍然只有38%的正確率.

教學反思：就一步如“當x>0時，-x<0，則f（x）=-f（-x）…”的推理就可以解答的問題，學生居然會學得如此困難，出乎教師的預料. 對學生解答的分析和訪談發現，根源是學生難以理解這種形式化推理的必要性和合理性. 教師自覺此題的解法簡單明了，認為只要示范講明，學生模仿著做就可以掌握了. 豈料學生總是傾向于用自己的理解（即學習過程中形成的思維表象）來解題，因為學生頭腦中的“表象”是思考時最先跳出來的、最活躍的心理因素[2]. 案例一和案例二都表明了對數學的理解是學生自主建構的，把學生當作知識的容器，一味地講授灌輸式的數學教學效果是很差的.課堂上要注意通過學生獨立嘗試練習后的師生互動，通過正例與反例的對比分析及獨立練習等用來豐富和完善學生的“基本活動經驗”和認知表象，這樣才能真正提高學生的理解水平和解題應變能力，這樣才是真正高效率的數學教學.

第三次（9月17日），在前“錯誤”課堂講評后，此題作為“錯題再練”，結果是68%的正確率，進步顯著.

第四次（9月19日），課堂的單元考試，此題是72%的正確率.

第五次（9月23日），此題是79%的正確率.

第六次（10月30日），當天下午第二節的課堂測試，此題居然只有26%的正確率. 絕大多數學生因為淡忘、沒有思路或思路不清而錯.

（3）代表性的學生個案學習進程與分析：

①同上，后進生吳：第一次、第二次屬于思路不清的錯誤，第三次正確，第四次考試錯誤，第五次正確，第六次屬于思路不清的錯誤.

②同上，中等生林：第一次、第二次、第三次、第四次都是屬于思路不清、邏輯混亂的錯誤，雖有訂正，但總是不按照教師示例的步驟推理，習慣于自己亂寫而錯. 第五次正確，第六次測試沒有思路，顯示空白.

③同上，優秀生黃：每次都正確.

3. 案例3：分段函數的單調性問題

（1）課后作業訓練的變式進程：第一次，作業為“已知f（x）=x2-2x-3a，x≥2，（a+2）x-1，x<2 是（-∞，+∞）上的單調遞增函數，求實數a的取值范圍”;后繼的變式作業只是對區間劃分和函數稍作了改變，比如加入了后面學習的指數函數或對數函數，形式和難度基本不變（詳略）.

（2）高一（13）班整體教與學的進程及分析：

第一次（9月12日），當天只在課堂上講析了一個范例，沒有匹配練習，結果是此題作為課后作業只有34%的正確率. 課堂范例分析能使學生對解決此類題目有一個大致的思路，但從作業效果來看，對這類較復雜的問題，沒有當堂的獨立練習和講評，大多數學生難以掌握思路.

第二次（9月17日），這是階段復習后的“錯題再練”作業，此題的結果還是34%的正確率.

第三次（9月19日），在課堂的單元考試中，此題作為填空題的第12題，只有38%的正確率.

第四次（9月21日），試卷講評后的“錯題再練”，此題是40%的正確率.

第五次（9月24日），又是“錯題再練”，此題是70%的正確率，終于取得了顯著的進步.

第六次（10月30日），課堂測試，此題居然只有18%的正確率，可怕的遺忘！

教學反思：通過作業分析和訪談發現，雖然課堂上學生聽懂了大致思路，但具體操作仍是生疏易錯，有些學生對含參數的函數畫示意圖感到困惑. 教師反思后再次講析此類題型時，把解法進行了“算法化”的分步操作處理，并且是講析一步讓學生做好一步的筆記，這樣易于學生模仿. 經過反復變式訓練后，終于取得了顯著的進步;但進步還是太慢，效率低下，如果早點改進教法，并集中、強化變式訓練，效率會更高.

（3）代表性的學生個案學習進程與分析（詳略）.

4. 案例4：班級整體的對比分析

第一次是在10月8日的高一年段月考中（考試內容是第一章到第二章的對數的運算，滿分120），（13）班的數學平均分是69.2分，比（11）班高6.6分，比其余12個平行班的總平均分高6.5分. 第二次是在11月16日的高一年段期中數學考試中（考試內容出自必修一，滿分150），（13）班的數學平均分是117.4分，比（11）班高6.4分，比其余12個平行班的總平均分高8.4分. 可見（13）班的數學平均分顯著高于其他對比班，進一步的各試題所得平均分的對比分析都表明了短期內造成如此顯著差距的一個主要原因就是（13）班的數學教學采取了教師自己設計的預設與生成結合的作業，實現了對核心重點的內容或題型的循環鞏固，以及變式遞進的訓練.

研究結論與建議

1. 研究結論

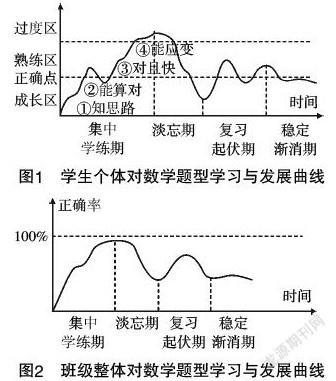
對基本題型的掌握是學生數學理解和能力發展的基礎，是數學教學的重要內容.結合上述案例分析和教學經驗，從一般性來看，學生個體或班級整體對數學相對較難題型的學習發展具有以下曲線顯示的階段和特征：

從數學題型學習與發展曲線可知，要提高教學效率，一是開始的學習要趁熱打鐵，集中連續地學練到位（以“講練糾”或“練糾”的方式變式遞進），并達到一定的熟練度，為后繼的變式提升奠定基礎;二是要科學設計練習讓知識循環鞏固，提升“長作業”練習體系. 而下列的數學教學方式是低效的：（1）課堂上一味地講授，缺乏師生互動和學生獨立的嘗試練習;（2）傳統的知識本位的線性前進的教與練，缺乏對前面所學知識的循環鞏固，這樣會導致學生學了后忘了前的“漏勺”式的低效教學現象的出現;（3）沒有系統的“長作業”式的鞏固提升變式訓練，這樣會導致學生的學練不到位，加之遺忘而功敗垂成;（4）訓練到位后的再重復訓練可能就是過度低效了;（5）學生缺乏新知識學習所必要的基礎，這是高一數學入門教學困難的首要原因.

2. 教學建議

結合研究結果和長期的教學經驗，筆者提出以下高效的高中數學教學的基本原則和策略：

（1）“以學為本，教服務于學”是保證教學效率的基本理念和前提. 教師頭腦中存在的潛意識的知識本位和教師本位的觀念使得教師認為教學就像“扔包袱”一樣把知識講清楚教給學生就行了，不關心學生實際的接受情況，結果是教學低效到不如自知. 所以保證教學效率首先是要樹立“以學為本，教服務于學”的理念，教師始終要有意識地“稚化”自己的思維，想學生之想，預學生之困，并跟蹤調查學情，這是發現學習問題和獲得適合學生的高效教學的前提.

（2）一條主線——螺旋上升，分層前進式的學生學練活動. 數學教學的落腳點不是教師“教完”，而是學生“練會”. 從前面“對數學題型學習與發展曲線”可知，適合學生數學認知發展規律的循環鞏固，螺旋上升式的數學學練活動對保持和提高數學教學效率是不可或缺的. 從案例研究中也會發現分層教學，盡量使每個學生獲得與之相適應的教與練，對提高教學效率，特別是防止和轉化學差生是不可或缺的.

（3）一個依托——教練一體系統優化的課后作業[3]. 傳統的線性前進的數學作業，無法滿足螺旋上升、分層遞進的數學教學要求，所以設計出一套高質量的教練一體系統優化的課后作業是高效數學教學的依托，也是破除低效的“題海戰術”的關鍵. 循環往復變式遞進的訓練是必需的，但要把握好“度”，這就是要根據作業中學生反饋的信息來看學練是否到位，還存在哪些問題，并據此及時調整后繼的教與練，所以課后數學作業要將預設和生成結合才能最好地適合學生，避免盲目低效的“題海”訓練，從而獲得高效的教學成果.

（4）一個保障——激勵與督促結合的教學管理. 從案例分析中可知，教師的嚴格管理，努力使每個環節的教學要求落實到位，是學生個體和班級整體有效學習進步的保障.

參考文獻：

[1] ?于新華，王新兵，楊之. 對“數學教學效率”研究的幾點思考[J]. 數學教育學報，2006（15）.

[2] ?李士锜. PME：數學教育心理[M]. 上海：華東師范大學出版社，2001.

[3] ?鐘志敏. 教練一體系統優化的三角函數教學[J]. 數學通報，2016，55（06）.