鋼板-高延性混凝土組合低矮剪力墻抗震性能試驗研究

鄧明科，劉俊超，張陽璽，劉海勃，景武斌

(1. 西安建筑科技大學土木工程學院，西安 710055；2. 西安建筑科技大學結構工程與抗震教育部重點實驗室，西安 710055；3. 中國電建集團西北勘測設計研究院有限公司，西安 710065；4. 西安五和土木工程新材料有限公司，西安 710055)

鋼板-混凝土組合剪力墻是高層及超高層建筑采用的一種新型組合結構，它具有減小墻體厚度、減輕結構自重等優勢[1]，還可以提高構件的承載力和變形能力[2]。但是，當剪跨比較小時，組合剪力墻的抗震性能和變形能力明顯降低，導致結構的地震損傷程度較大。

國外學者[3 ? 4]對帶加勁肋的雙鋼板剪力墻進行了試驗研究，結果表明此類剪力墻抗震性能良好，但是由于構造復雜、施工困難、造價偏高，其在工程應用中受到極大限制。呂西林等[5]對內置鋼板鋼筋混凝土剪力墻進行了試驗研究，結果表明鋼板對于提高構件的抗震性能效果十分明顯。陳麗華等[6]提出了一種新型的配置L 形拉結件的雙鋼板-混凝土組合剪力墻，結果表明此新型組合剪力墻具有較高的承載力和較好的延性。李小軍和李曉虎[7 ? 8]研究了應用于核電工程的雙鋼板-混凝土組合剪力墻，并提出了剪力墻試件的受彎承載力計算公式。聶建國等[9 ? 10]進行了低剪跨比雙鋼板-混凝土組合剪力墻擬靜力試驗研究，結果表明雙鋼板-混凝土組合剪力墻具有良好的承載能力、抗側剛度。但是，在低矮剪力墻的研究中發現，由于混凝土的脆性和開裂軟化特點，墻體內部的混凝土破損嚴重，導致結構的延性較差，且地震損傷后難以修復。

高延性混凝土[11 ? 14](high ductile concrete，簡稱HDC)是一種具有高韌性、高抗裂性能和高耐損傷能力的新型結構材料，具有明顯的受拉應變硬化和多裂縫開展特性。基于HDC 的力學性能優勢，采用HDC 替換混凝土應用于鋼框架組合剪力墻[15]，可使構件的抗震性能顯著提高，實現具有延性的剪切破壞；在鋼板-HDC 組合連梁的擬靜力試驗研究[16]中發現，連梁基體采用HDC 可提高構件的塑性變形和耐損傷能力，HDC 與鋼腹板的協同工作性能良好，有利于鋼腹板抗剪作用的發揮。基于以上研究，將HDC 與鋼板進行組合，提出外包鋼板-HDC 組合低矮剪力墻，并通過擬靜力試驗，研究不同軸壓比、不同配鋼形式對低矮剪力墻的破壞形態、滯回性能、承載能力、變形能力、耗能能力和剛度退化的影響，為鋼板-HDC 組合低矮剪力墻的工程應用提供依據。

1 試驗概況

1.1 試件設計

本試驗共設計了5 片低矮剪力墻，其中1 片HDC 低矮剪力墻(HW)，2 片內置鋼板-HDC 組合低矮剪力墻(SHW-1，SHW-2)，2 片外包鋼板-HDC組合低矮剪力墻(DHW-1，DHW-2)。HDC 的強度等級按C50 設計，所有試件的剪跨比均為1.0，墻體截面尺寸均為1000 mm×100 mm，剪力墻高度均為900 mm。頂部加載梁的高度為200 mm，水平荷載加載點至墻體底部的距離為1000 mm，底部加強區高度為200 mm，采用槽鋼進行約束及對拉螺栓進行有效連接，以便試件與底梁連接，底梁采用可替換式鋼底梁裝置。

試件HW 兩端設置分段約束箍筋[17]；試件SHW-1、SHW-2、DHW-1、DHW-2 兩端設置方鋼管HDC 端柱，方鋼管內布置4 根直徑16 mm 的豎向受力鋼筋；試件SHW-1、SHW-2 鋼板兩側分布有直徑6 mm 的水平和豎向分布鋼筋，DHW-1、DHW-2 試件外包鋼板通過對拉螺栓與內填HDC 形成有效連接，對拉螺栓布置尺寸為100 mm×100 mm。方鋼管和鋼板均采用Q235 鋼材。鋼筋和鋼板與端柱及底板均采用焊接連接。

試件SHW-1、DHW-1 的設計軸壓比為0.7，豎向荷載為1294 kN (12.94 MPa)，試件HW、SHW-2和DHW-2 的設計軸壓比為0.5，豎向荷載為924 kN(9.24 MPa)。其中，設計軸壓比 n=Nc/(fcAw)， Nc為軸壓力設計值(可取Nc=1.25 N ， N為軸壓力試驗值)； fc為混凝土軸心抗壓強度設計值；Aw為剪力墻總截面面積。5 片低矮剪力墻的具體參數如表1所示，各試件的尺寸及配筋見圖1。

1.2 材料力學性能

HDC 主要由PVA 纖維、Ⅰ級粉煤灰、P·O 42.5R普通硅酸鹽水泥、精細河砂、礦物摻合料、水和

高效萘系減水劑按一定比例制備而成。PVA 纖維的體積摻量為1.5%，纖維各項力學性能指標如表2所示。

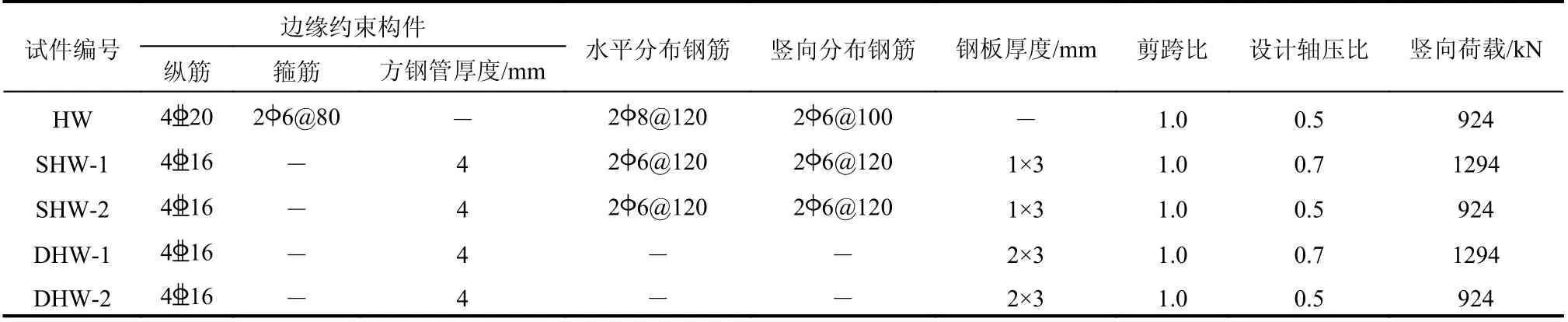
表1 試件參數Table 1 Parameters of specimens

HDC 基本力學性能見表3，其中： ft為軸心抗拉強度，采用截面尺寸為50 mm×15 mm 的狗骨型試件通過單軸拉伸試驗測得； fcu為采用邊長為100 mm 的立方體試塊測得的抗壓強度； fp為采用100 mm×100 mm×300 mm 的棱柱體測得的抗壓強度；鋼筋、方鋼管和鋼板的力學性能如表4 所示。

表2 PVA 纖維各項性能指標Table 2 Performance indicators of PVA

表3 HDC 的力學性能Table 3 Mechanical properties of HDC

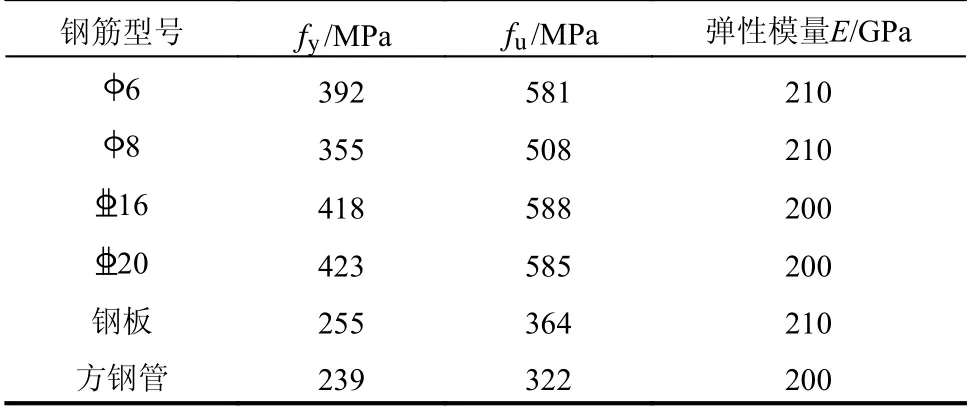
表4 鋼材的材料性能Table 4 Material properties of steel

1.3 試驗加載及測試內容

對本試驗的5 片剪力墻進行擬靜力試驗，采用荷載-變形雙控制的加載制度，先施加預定的豎向荷載并保持不變，試件屈服前，以荷載控制并進行分級加載，每級荷載循環1 次，極差100 kN；試件屈服后，在屈服位移的基礎上以4 mm 為極差采用位移控制進行加載，每級循環3 次。加載至試件承載力降至峰值荷載的85%之后，停止加載。試驗中以推向為正，拉向為負。試驗加載裝置如圖2 所示。

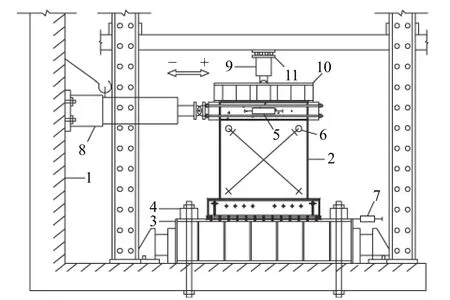
圖2 試驗加載裝置Fig.2 Test setup

試驗共安裝了4 個位移計，分布情況如下：試件頂部加載梁中部布置一個位移計，以測試墻體頂點位移；在墻體一側沿對角線方向各布置一個位移計，以測試墻體的剪切變形；在底梁端部安裝一個位移計，以測量試件的整體水平滑移。

2 試驗現象

5 個試件的最終破壞形態如圖3 所示，開裂損傷發展過程和破壞形態描述如下：

1) 試件HW

當加載到300 kN 時，墻體下方出現水平裂縫；隨著水平推力的增加，原有裂縫發展并延伸，形成交叉裂縫，墻體下側出現多條剪切斜裂縫；加載到600 kN 時，試件屈服，改用位移控制加載；當加載到15 mm 時，墻體角部HDC 出現壓酥現象；加載至19 mm 時，墻體底部出現一條剪切滑移裂縫，兩個主對角線形成明顯的交叉剪切斜裂縫，試件破壞，為彎曲屈服后的剪切破壞。

2) 試件SHW-1 和SHW-2

試件SHW-1 和SHW-2 的破壞過程類似，以試件SHW-1 為主要描述對象。對于試件SHW-1，當加載到500 kN 時，墻體底部出現細密的水平裂縫和斜裂縫；加載到900 kN 時，墻體出現大量剪切斜裂縫；加載到1000 kN 時，試件屈服，改用位移控制加載；當加載到17.5 mm 時，方鋼管底部受壓外鼓；加載到25.5 mm 時，墻體下部HDC保護層外鼓剝落，剪切斜裂縫、水平裂縫貫通，墻體上部出現較寬豎縫，墻體的方鋼管屈曲明顯，試件破壞，破壞形式為彎剪破壞。

圖3 試件破壞形態Fig.3 Failure modes of specimens

與試件SHW-1 相比，SHW-2 的墻體腳部HDC壓酥現象較輕，當加載到21 mm 時，鋼管屈曲明顯，加載到33 mm 時，試件破壞，破壞形式為彎剪破壞。

3) 試件DHW-1 和DHW-2

試件DHW-1 和DHW-2 的破壞過程類似，以試件DHW-1 為主要描述對象。對于試件DHW-1，當加載到600 kN 時，試件右側的方鋼管底部開始屈服；加載到900 kN 時，外包鋼板開始屈服，角部鋼板輕微外鼓；加載到1100 kN 時，外包鋼板交叉外鼓，方鋼管底部外鼓屈曲增加，試件開始屈服，改用位移控制加載；當加載到19 mm 時，墻體的方鋼管端柱側面明顯外鼓，槽鋼包圍區域內的HDC 被拉起，鋼板交叉外鼓；加載到31 mm時，雙鋼板外鼓明顯，底部加強區的HDC 和暗柱被拔出，墻體的對拉螺栓有一部分已經松動，試件破壞。

與試件DHW-1 相比，當加載到1100 kN 時，DHW-2 的外包鋼板開始屈服，加載到20 mm 時，試件底部加強區HDC 略微翹起，加載到28 mm時，試件破壞，試件底部加強區的HDC 和暗柱未被拔出來。

從圖3(f)可看出試件DHW-1 和DHW-2 破壞后，外包鋼板內部的HDC 材料基本完好，無破碎現象，兩個試件的破壞形式均為彎曲破壞。說明將HDC 材料應用到外包鋼板-混凝土組合剪力墻中可以減小試件破壞的損傷程度，地震損傷后更容易修復。

3 試驗結果分析

3.1 滯回曲線

5 片剪力墻的滯回曲線如圖4 所示。各試件的滯回曲線的特點如下：

1) 加載初期，試件均處于彈性段，滯回曲線在往復荷載作用下基本呈線性，試件殘余變形很小，剛度退化不明顯。屈服后，試件的滯回曲線開始明顯偏離直線，滯回環逐漸變得飽滿；各試件的滯回環基本均呈尖梭型，表現出良好的耗能能力。

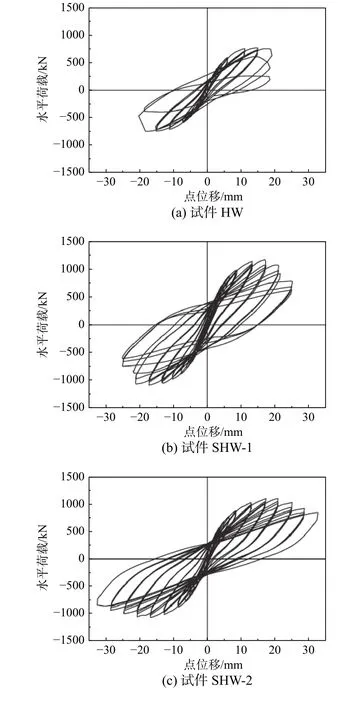
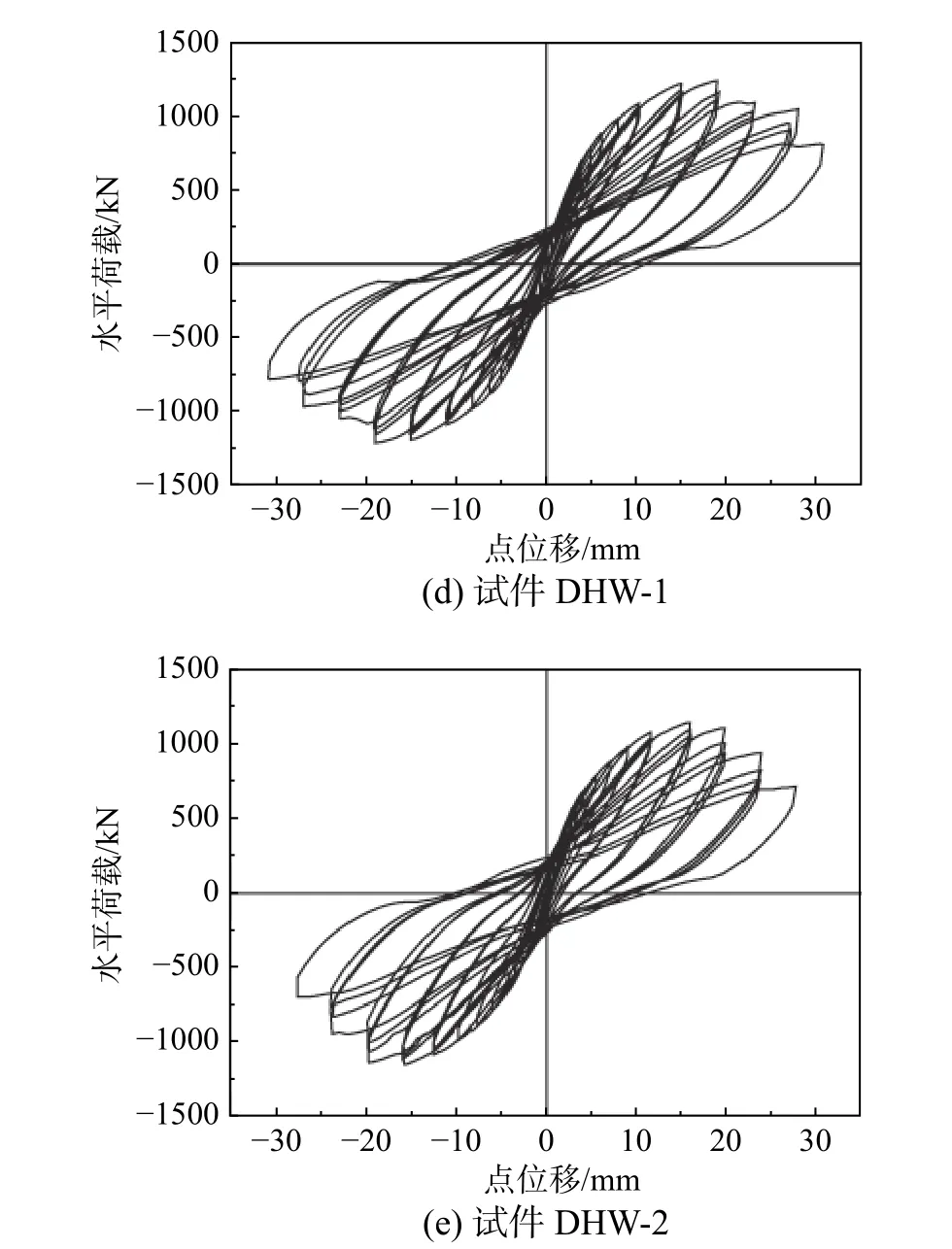
圖4 荷載-位移滯回曲線Fig.4 Load-displacement hysteretic loops

2) 與試件HW 相比，鋼板-HDC 組合低矮剪力墻的滯回環更飽滿，每一級位移循環中強度退化更小，峰值荷載后承載力和剛度退化更緩慢，表現出更好的變形能力。

3) 鋼板-HDC 組合剪力墻中，外包鋼板-HDC組合剪力墻的滯回曲線具有相對明顯的捏攏效應，該現象與剪力墻兩側鋼板外鼓并與內部HDC界面脫粘有關；軸壓比從0.5 增大到0.7 時，內置鋼板- HDC 組合剪力墻的滯回特性明顯降低，而對外包鋼板-HDC 組合剪力墻的滯回性能無明顯影響。

3.2 骨架曲線

將荷載-位移曲線中各滯回環峰值點相連可得到試件的骨架曲線，如圖5 所示。各試件骨架曲線的特點如下：

1) 與試件HW 相比，鋼板-HDC 組合低矮剪力墻的骨架曲線彈性段明顯變長，峰值荷載顯著提高(47.4%～65.6%)，峰值后的承載力下降更平緩，可見，將HDC 與鋼板組合應用于低矮剪力墻，可顯著提高構件的延性和塑性變形能力，其原因是鋼板與HDC 能夠很好地協同工作。

圖5 試件骨架曲線Fig.5 Skeleton curves of specimens

2) 軸壓比相同時，外包鋼板-HDC 組合剪力墻峰值荷載大于內置鋼板-HDC 組合剪力墻；軸壓比增大到0.7 時，內置鋼板-HDC 組合剪力墻(SHW-1)極限位移大幅降低，其原因是內置單鋼板受壓屈曲，對受壓區HDC 形成外鼓力，降低了墻截面的變形能力；而外包鋼板-HDC 組合剪力(DHW-1)的極限位移沒有降低，同時，試件DHW-1 極限位移大于試件DHW-2，可見外包鋼板-HDC 組合剪力墻在軸壓比為0.7 時依舊具有較好的塑性變形，其原因是雙鋼板可對(鋼板內側的)HDC 形成有效約束作用，使其變形能力提高，進而提高了墻體的極限位移。

3.3 變形能力和延性分析

以極限位移角θ(構件的極限位移與試件高度之比)衡量構件的延性。根據“能量等值法”來確定試件的屈服點，參考《建筑抗震試驗方法規程》[18]，取荷載下降至峰值荷載的85%時所對應的曲線上的點為極限位移點，H 為加載點到剪力墻底部截面的高度。各試件的骨架曲線特征點和延性指標的計算結果如表5 所示，其中延性系數μ為試件的極限位移與屈服位移之比。由表5可知：

1) 與試件HW 相比，試件SHW-2 和DHW-2的延性系數分別提高32%和10%、極限位移角分別提高63%和30%，可見鋼板-HDC 組合剪力墻的塑性變形相比HDC 剪力墻有較大提高。

2) 軸壓比從0.5 增大到0.7，試件SHW-1 的延性系數和極限位移角相比試件SHW-2 降低了18%和22%，試件DHW-1 的延性系數和極限位移角相比試件DHW-2 提高了7%和13%，可見軸壓比為0.5 時，內置鋼板-HDC 組合剪力墻有利于提高墻片的塑性變形，而軸壓比為0.7 時，外包鋼板-HDC 組合剪力墻依舊具有較好的塑性變形。

3) 軸壓比從0.5 增大到0.7 時，試件DHW-1的塑性變形略大于試件DHW-2，其原因是雙鋼板可對(鋼板內側的)HDC 形成約束作用，使其變形能力提高，進而提高墻片的截面曲率；軸壓比為0.7 時，試件SHW-1 的塑形變形小于試件DHW-1，其原因是隨著軸壓比增大，內置單鋼板受壓屈曲，對受壓區HDC 形成外鼓力，降低了墻截面的變形能力。

表5 各試件的特征點及延性指標Table 5 Characteristic points of specimens and ductility indices

3.4 耗能分析

以試件達到屈服點、峰值點和極限點的累計耗能評價墻片的耗能能力，如表6 所示。

從表6 可以看出：

1) 試件SHW-2 在屈服點、峰值點以及極限點下的累積耗能是試件HW 的2.03 倍、3.30 倍和4.14 倍；試件DHW-2 在屈服點、峰值點以及極限點下的累積耗能是試件HW 的1.09 倍、1.66 倍和2.64 倍，可見鋼板 -HDC 組合低矮剪力墻的抗震性能遠遠優于HDC 剪力墻。

表6 各試件的累積耗能Table 6 Energy dissipation of specimens

2) 在屈服點、峰值點以及極限點下，試件SHW-1的累積耗能相比試件SHW-2 降低了54%、38%和24%，試件DHW-1 的累積耗能相比試件DHW-2提高了44%、67%和20%，可見軸壓比為0.7 時，外包鋼板-HDC 剪力墻依舊表現出較好的抗震性能。

3.5 剛度退化

采用割線剛度表現試件在水平低周反復荷載作用下的剛度退化特性。割線剛度K 按式(1)計算，圖6 為各試件的剛度退化曲線。

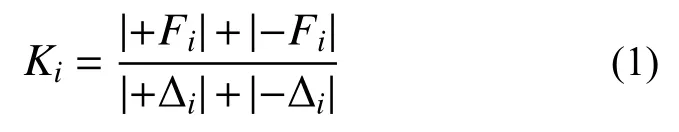
式中： Ki為第i 級加載下的割線剛度；+Fi和?Fi分別為第i 級加載下正、反水平峰值荷載值；+?i和??i分別為第i 級加載下正、反水平峰值荷載值對 應的位移。

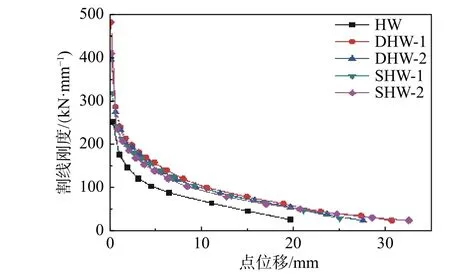
圖6 剛度退化曲線Fig.6 Curves of stiffness degradation

由圖6 可以看出：

1) 試件在整個加載過程中的割線剛度隨著位移的增大逐漸減小，隨著位移的進一步增大，剛度退化曲線都趨于平穩，剛度退化速率越來越低，說明試件在加載后期的受力特性逐漸穩定。

2) 4 個鋼板-HDC 組合低矮剪力墻的剛度退化曲線明顯高于試件HW，說明鋼板-HDC 組合低矮剪力墻更有利于抗震。

3) 4 個鋼板-HDC 組合低矮剪力墻的剛度退化曲線基本重合，說明軸壓比的影響對鋼板-HDC 組合低矮剪力墻的割線剛度影響不大。

4 正截面受彎承載力理論分析

4.1 材料本構模型

4.1.1 HDC 受壓本構模型

HDC 的單軸受壓本構方程采用文獻[19]提出的兩段式模型，其表達式為：

式中：A 為HDC 受壓初始切線模量 Ec與峰值應力點處割線模量 Eg的比值；B 為與纖維摻量及HDC軸心抗壓強度有關的參數； ε0為HDC 峰值壓應變； fp為HDC 峰值壓應力。

4.1.2 HDC 受拉本構模型

HDC 的單軸受拉本構方程采用文獻[19]建議的雙線性模型，具體表達式為：

式中： σtc為開裂強度； εtc為開裂拉應變； εtu為極限拉應變； Et為彈性段拉伸彈性模量； Eh為應變硬化段硬化彈性模量。

4.1.3 鋼筋本構模型

試件采用的熱軋鋼筋具有明顯的屈服平臺，本文采用理想彈塑性模型：

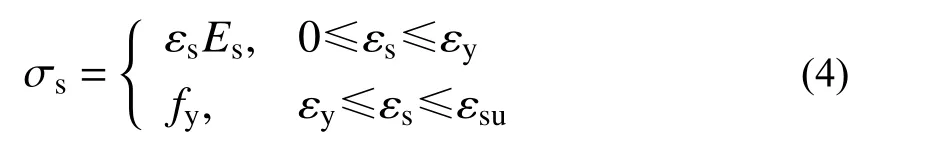
式中： fy為鋼筋屈服應力； Es為鋼筋彈性模量；εy為鋼筋屈服應變； εsu為鋼筋設計極限應變。

4.2 等效矩形應力圖形

進行鋼筋混凝土構件正截面計算時，通常將混凝土實際的應力圖形轉換成一等效矩形應力圖形，以簡化計算[20]。參考文獻[21]可得HDC 的等效應力圖形系數 α 和 β，如表7 所示。等效矩形應力圖形的受拉(壓)區高度為βxp，等效應力為 αf，xp為實際受拉(壓)區高度，f 為HDC 極限抗拉強度 ftu或抗壓強度 fp。

4.3 正截面受彎承載力計算公式推導

對外包鋼板-HDC 組合低矮剪力墻，當墻體受壓區邊緣HDC 應變達到峰值壓應變 ε0時，剪力墻達到最大承載力。在計算剪力墻水平承載力時，可以基于以下假設：1) 忽略對拉螺栓對剪力墻受彎承載力的作用；2) 不考慮方鋼管及鋼板對HDC的約束作用；3) 截面應變分布符合平截面假定；4) 鋼板的應力-應變關系為理想彈塑性。

考慮HDC 的抗拉作用時，引入系數λ[21]計算HDC 受拉區有效高度，則受拉區高度為xt=λx，構件受彎承載力計算模型如圖7(a)所示；當(1+λ)·x≥HW時，受拉區邊緣沒有退出工作，受拉區高度為xt=HW?x，計算簡圖如圖7(b)所示。由于墻體截面較高，計算水平承載力時，只有部分鋼板達到屈服，因此，僅考慮ηx[22]范圍外的鋼板。λ 、η[22]取值為：

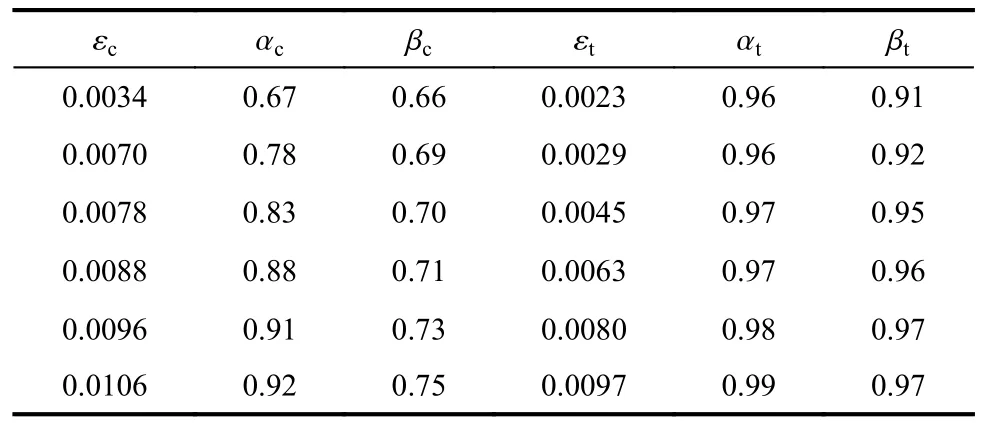
表7 HDC 等效應力圖形系數Table 7 Equivalent rectangular stress block parameters

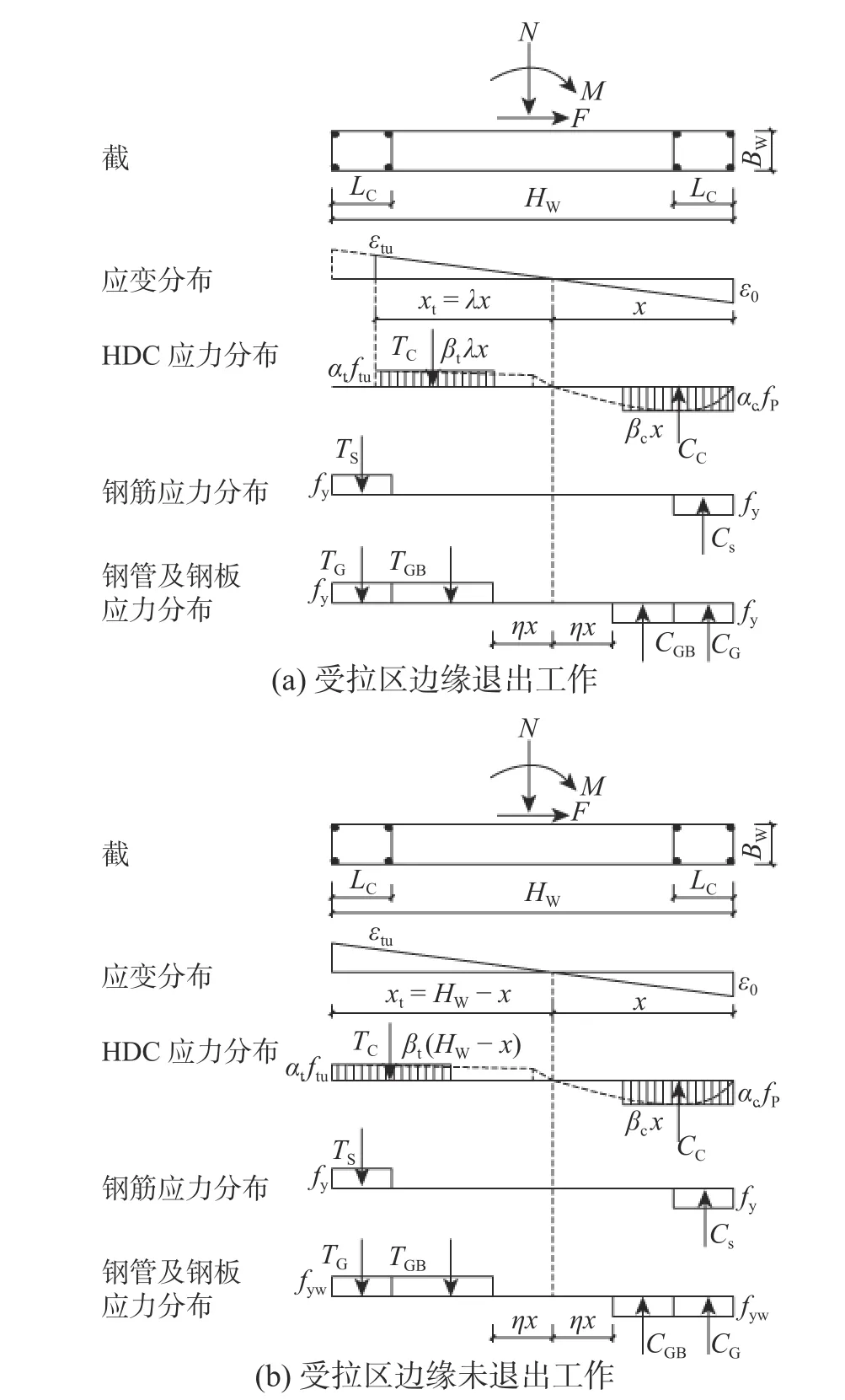
圖7 截面峰值荷載狀態受力示意圖Fig.7 Stress and strain profiles of wall at peak loading state

式中： fyw為鋼板屈服強度；Esw為鋼板的彈性模量。

由圖7 所示，截面上各合力的關系式為：

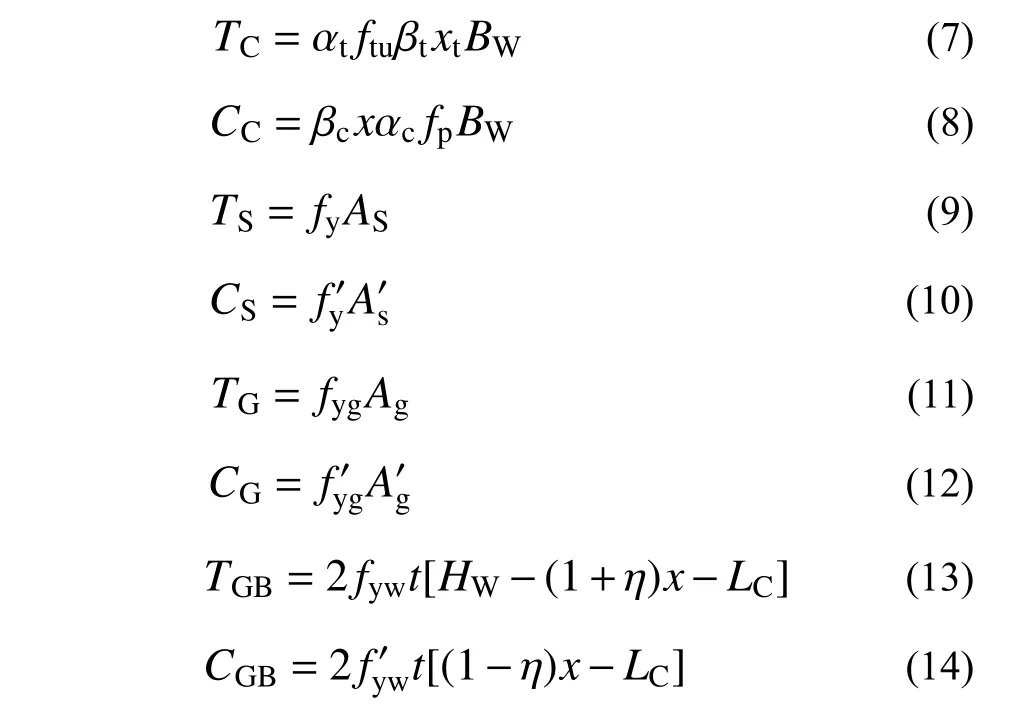
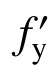
由豎向力的平衡條件可得：

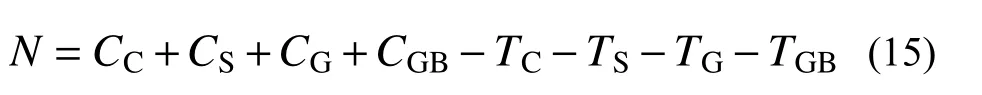
對受拉區方鋼管截面形心處取矩，由平衡條件可得：

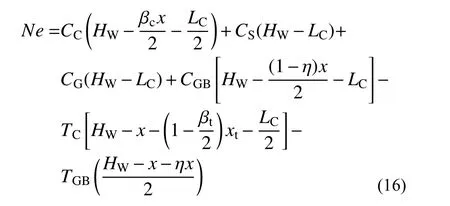
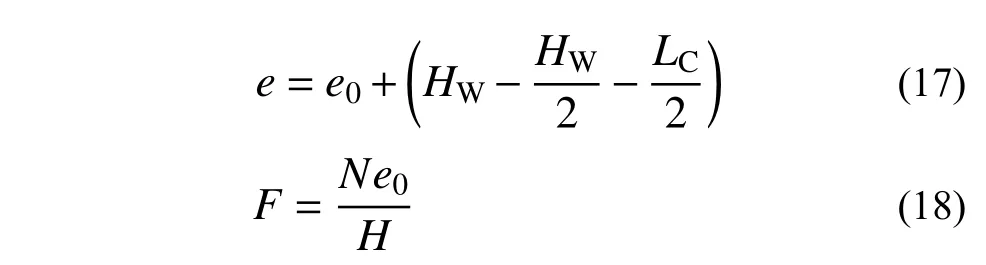
式中：N 為剪力墻所受的豎向力；e 為豎向力作用點到剪力墻受拉方鋼管截面形心的距離； e0為偏心距；F 為試件的水平承載力。

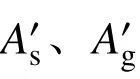
對于內置鋼板-HDC 組合剪力墻，將內置鋼板外的豎向鋼筋換算成面積相等且連續的鋼筋腹板，然后按外包鋼板剪力墻的方法分析計算。

4.4 計算值與試驗值分析對比

按式(7)～式(18)計算，表8 列出了4 片鋼板-HDC 組合低矮剪力墻試件水平承載力的計算值和試驗值。由表8 可以看出，計算值與試驗值吻合較好。

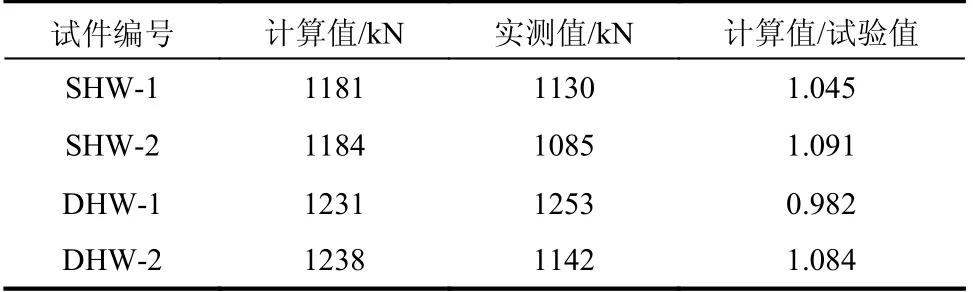
表8 計算值與試驗值的比較Table 8 Comparison between calculated and test values

5 結論

對5 片低矮剪力墻的各項抗震性能指標及抗彎承載力進行分析，可得到以下結論：

(1) 外包鋼板-HDC 組合低矮剪力墻在破壞階段，內部的HDC 基本完好，鋼板和HDC 共同受力，墻體的整體性能較好，有利于改善剪力墻的破壞形式，使墻體發生具有延性特征的彎曲破壞。

(2) 4 片鋼板-HDC 組合低矮剪力墻的抗震性能明顯優于HDC 低矮剪力墻，其承載力以及變形能力明顯提高，具有優良的抗震性能。

(3) 4 片鋼板-HDC 組合低矮剪力墻的承載能力和剛度受軸壓比的影響較小；當軸壓比從0.5 增大到0.7 時，內置鋼板-HDC 組合低矮剪力墻的變形能力和耗能能力有所降低，外包鋼板-HDC 組合低矮剪力墻的變形能力和耗能能力沒有降低；當軸壓比為0.7 時，外包鋼板-HDC 剪力墻依舊表現出較好的抗震性能和耐損傷能力。

(4) 給出的鋼板-HDC 組合低矮剪力墻受彎承載力計算公式，計算值與試驗值吻合較好，表明此計算方法合理和實用。