匹配市場算法

匹配，是人們社會生活中許多問題的一種抽象。例如高考錄取，是考生與大學之間的匹配;學生畢業了找工作，是畢業生和用人單位之間的匹配;男女婚戀，自然也是一種匹配。這些匹配的形成過程，常常會在某種制度（包括法律法規、約定俗成的做法等）下進行。顯然，這些匹配的結果如何（與制度很有關系），具有重大的社會意義。于是，匹配的制度設計就成為一個很有價值的問題。2012年諾貝爾經濟學獎，就頒發給了兩位在這方面作出突出貢獻的學者。

匹配市場模型

上面這些例子的共性，一是有雙方，每一方有多個對象，二是互選，事情不能一廂情愿，糾結就發生在這里。其實，即便不是互選，由于資源有限，常常也會很難搞定。想一想那些熱門的大學吧，就算大學不挑學生，但宿舍床位有限，食堂空間有限，不可能容納所有希望去的學生，最后總有一個怎么安排的問題。

下面我們來討論一種相對單純點的匹配問題，看看算法思想如何在其中發揮作用。設想有這樣一個情境：你有A、B、C、D有一定價值的4件舊物品希望送出去，現在有4個人W、X、Y、Z有興趣要。當然，一人分得一件是比較合適的，也就是說要在物品和人之間形成一個匹配。可物品是不一樣的，某兩個人可能最想得到某同一件物品，該如何安排呢？

按照經濟學的語言，這意味著需求和供給之間有沖突。盡管你只是想把物品送出去，并沒有想賺錢，但我們不妨從市場的觀點來探討一種解決方案。你告訴他們，每人對每件物品給出一個以金額表達的價值，對應他愿意支付的最大數額以得到相應的東西，但超過了就不值了。這樣，所表達的價值就反映了人們對不同物品的喜愛程度。假設他們告訴你了，于是你就面對如圖1（a）所示的一個局面。

圖1中的4×4數據矩陣就是W、X、Y、Z對A、B、C、D的估值。每一行對應一個人，每一列對應一件物品。從中我們看到W最喜歡的是B，因為他給出的估值是9，在第一行中最大。而X和Z最喜歡的都是A，因為都給出了最大估值，于是有沖突了。圖1（b）與（a）含義是一樣的，只是另外一種圖示，便于后面的算法討論。

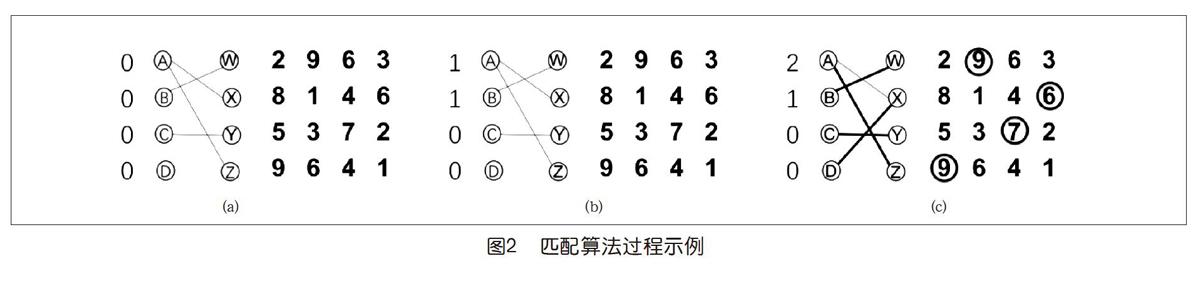
怎么辦呢？人們參照市場經濟的一種基本精神——物以稀為貴——設計了一個算法。該算法要通過為物品確定一組價格，來達成某種最優意義下的物品分配。下面先就圖1的例子，通過圖2中的三個圖來解釋這個算法的步驟，接著再討論它的一些性質。

先看圖2（a），它和圖1不同的是左邊添加了4個0，用以表示A、B、C、D的初始嘗試價格。同時我們也注意到，在原先的物品（A、B、C、D）和人（W、X、Y、Z）之間添加了一些邊（線），形成了一個二部圖，也就是節點可以分成左右兩邊，邊只是跨兩邊節點的圖。在這個算法中，那些邊的含義很關鍵，表示“最大差價”。例如，W和B之間的邊，意味著9-0=9是W目前看到的最合適的物品，于是表達了“W最希望得到B”的含義。此時，初始價格為0，最大差價也就對應最大價值了。若價格變了，最大差價自當改變，于是二部圖中的邊也就要相應調整了。

下面來重點了。我們看到圖2（a）中表現出了一些沖突。例如，從W、X、Z沿著邊向左看過去，只能看見A和B。也就是說三個人表達的最愛集中在兩個物品上，因此沒法都照顧到！怎么辦？物以稀為貴，讓那些供不應求的物品加點價！于是我們看到了圖2（b），其中A和B的價格提升到了1。這里的算法規則是讓二部圖中的邊總是對應最大差價。不過，就這個例子的當前數據而言，邊還是那些，因此二部圖的樣子沒有變。

下面是另一個要點。可以看到圖2（b）中依然有W、X、Z三個“爭搶”A和B兩個的現象。我們可以繼續給A、B加價。不過，還可以看到X和Z要的都是A，也是一種“供不應求”現象，于是也可以就單給A加價。這里是想說，加價的方式不唯一，只要是針對“供不應求”現象都可以。不同的選擇不會影響最后結果的性質（可能對效率有些影響，但不是本文重點）。假設我們現在就選擇只給A加價。

現在看圖2（c），A的價格提升到了2。我們看到，按照“最大差價”原則確定的物品和人之間的邊，二部圖發生了一個關鍵性變化——X現在認為也可以要D了，A和D對他來說差價都是6。于是，就浮現出一種無沖突安排，也叫完美匹配：A—Z，B—W，C—Y，D—X。

這樣一種安排意義重大。首先，每個人得到的都是對他而言差價最大的物品，也就是說他不可能通過要求換一個物品來獲得更大的差價。再者，如果我們看4件物品對于它們的獲得者的價值，對應圖2（c）右邊估值矩陣上圈出來的4個數字，滿足一個令人興奮的性質：它們的和是該矩陣上不同行不同列元素之和的最大值。這意味著，盡管并不是每個人都得到了最初最想要的物品（如X沒有得到A），但這種分配實現了一種總體價值最優，稱為達到了社會最優。

匹配市場算法

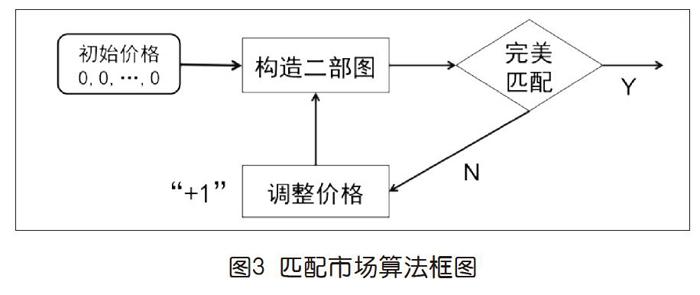
上面的例子，讓我們看到了借助市場“無形之手”——通過價格調整供需關系——得到的一種匹配的算法。一般地，給定任何非負整數估值矩陣，圖3所示即為這個算法的框圖。

一共有四個框，其中“初始價格”框沒什么說的。

“完美匹配”是判斷在二部圖上是否出現了無沖突的匹配關系。圖論告訴我們，如果沒有完美匹配，就意味著存在那種供不應求的沖突情況，也稱為存在受限組，即二部圖一邊的節點子集，大于鄰居節點集。

如果發現了在“人”一邊存在一個受限組和它對應的“物品”集合，“調整價格”就是很簡單的事情，即給那些物品的價格+1。在前面的例子中已經提到，在任何受限組基礎上做這種價格調整都會得到一致的結果。

而基于當前價格按照最大差價原則重新“構造二部圖”，確定該有哪些邊，也是直截了當的，即后面討論中會看到的。其中，取得max的k（可能多個）就指示“人”節點i就和“物”節點k之間有一條邊。

難點在哪里？在于如何判斷一個二部圖中是否存在一個完美匹配。對于圖2所示的例子，規模很小，我們憑目測就可以斷定（a）和（b）中沒有完美匹配，（c）就有了。但一般來說這是不容易的。體會一下這個難度，請看圖4。其中展示了四個二部圖，你能看出哪些有完美匹配嗎？如果沒有，能指出一個受限組嗎？

也許，你目測能力很強，看到（a）中不存在完美匹配，因為有受限組{a，b，c，e}，它們對應到左邊只有{1，3，6};還能看到（c）中存在完美匹配a—4，b—1，c—3，d—2，e—6和f—5。但你肯定感到了這是一個相當困難的任務，需要用計算機來解決。的確，為了使圖3所示的框架性算法能夠實現，在“完美匹配”判斷框要啟用一個子算法，相當于調用子程序。

有多種不同的方法來判斷一個二部圖是否存在完美匹配。其中之一，就是利用本欄目在2020年8月刊上介紹的求網絡最大流的算法。下面，就來看網絡流問題和這里的匹配問題是怎么聯系起來的。

回顧網絡最大流問題。它針對一個有源節點（s）和目標節點（t）的加權有向圖，確定從源到目標能夠實現的最大流量。下面我們會看到，有一種相當直接的方式，將判斷兩邊都有n個節點二部圖是否存在完美匹配的問題實例轉換為一個網絡最大流問題的實例，以至于后者的最大流量達到n，當且僅當前者存在一個完美匹配。

我們用如上頁圖5中的例子來解釋這個對應關系。（a）是要判斷是否存在完美匹配的二部圖，（b）是一個網絡最大流問題的實例。它基于（a），添加了兩個節點s和t，s連到右邊所有節點，t連到左邊所有節點;給所有邊賦予從右向左的方向，且令每條邊的權值均為1。

不難看到，如果圖5（b）中s到t的最大流量達到了n，注意到每條邊的權重均為1，就意味著從s到t有n條中間節點無重用的路徑，也就是（a）中有完美匹配，對應那些從s到t路徑中的中間邊。反之，如果（b）中s到t的最大流量小于n，意味著（a）中不存在n條端節點無沖突的邊跨接在左右兩邊，也就是沒有完美匹配了。此時，記L和R為二部圖中實現最大流的左、右兩邊的節點集合，受限組就是R加上右邊任一其他節點，在匹配市場算法中需要加價的就是L中的節點。以圖5（b）為例，能發現從s到t的最大流量是5，具體實現為s→a→1→t，s→b→3→t，s→c→6→t，s→d→2→t，s→f→4→t，小于節點數6，因而二部圖5（a）中不存在完美匹配，需要給節點1，2，3，4，6加價。

上述這一段討論有特別意義。當算法學習積累到一定程度，面對新的問題，往往有可能借用先前針對不同問題的算法。此時，關鍵在于要能在兩個問題之間做適當的“映射”，能夠從對老問題的解中“解釋”出對新問題的解來。

匹配市場算法的性質

至此，對圖3描述的匹配算法還能提什么問題嗎？至少還可以問兩個問題。第一，在調整價格的時候為什么總是“+1”？一次多加點會不會效率高一些？例如，從圖2（a）到圖2（b）似乎沒起任何作用，如果一次性加2，就會省下一輪迭代。第二，算法是以完美匹配的形成作為終止條件的，為什么一定會形成呢？

這兩個問題其實有關聯。看圖6所示n=2的小例子，調整價格的時候做“+2”，會出現什么現象。

可以看到，調整價格時做“+2”，整個情形就會在兩種狀態下無限循環往復，形成不了具有完美匹配的二部圖。下面就來證明，“+1”則會保證具有完美匹配二部圖的形成，即該算法一定會結束。

一般而言，算法是作用在某些數據上的處理過程。那些數據會在這個過程中得到某些改變。為了證明一個算法過程一定結束，尤其是對一些“框架性算法”（其結束條件可能是比較高層次的描述，就像這里的“出現了具有完美匹配的二部圖”），一種很有用的方法是選擇適當的數據對象，證明在算法過程中其值是單調有界的。這種方法本欄目在2020年8月刊討論網絡最大流算法時就用過。當時的結束條件是“不再有從s到t的增量路徑”，我們選取的數據對象是從s出發的剩余容量總和。

對本文討論的匹配市場算法，涉及的量包括估值矩陣中的值（在算法過程中不變）和在過程中變化的價格（初始為0）。為方便討論起見，用V來表示估值矩陣，a表示動態調整的價格向量，如圖7所示。

我們基于它們構造一個數據對象P如下。它包括兩個求和項，第二項是當前價格之和，第一項對應當前價格下的最大差價之和。下面來證明P在算法執行過程中具有“單調減且有下界”的性質。

在理解了算法操作的基礎上這個證明不難。由于“+1”涉及至少一個物品，第二項在算法的每一輪一定是遞增的，如果涉及了m個物品，也就是增加了m。對應到二部圖中的受限組，則至少涉及m+1個人，也就是在第一項中至少有m+1個max會減少1。減的多增的少，整個就是單調減了。如果是“+2”，第二項將增2m，但就不能保證第一項減量超過2m了。請讀者思考為什么。

為什么有下界呢？只要注意到V是給定不變的和下面的推導式就可以了，其中不等號是取k=i所致。

好了，到這里基本就完成了關于一個重要的匹配市場算法的討論。值得問的一個問題是，算法過程并沒有直接針對要獲得匹配估值總和的最大值，它只管按照物以稀為貴的原則調整價格，人們按照自己的估值和當前價格做對自己最有利的訴求表達（二部圖中以最大差價為指示的邊），但“無意中的”結果就是社會最優。這是必然的嗎？答案是肯定的。這個模型可以看成是對“無形之手”理論的一種非平凡的具體詮釋。

參考文獻

[1]David Easley， Jon Kleinberg.網絡、群體與市場[M].李曉明，等，譯.北京：清華大學出版社，2011，10：175-185.

[2]李曉明.網絡流問題[J].中國信息技術教育，2020（15-16）：16-21.

注：作者系北京大學計算機系原系主任。