有效理解算理的路徑探討
汪東興

摘 要 算理是計算的理論依據,是計算教學中邏輯思維的運用和體現。教師要幫助學生充分理解算理,必須做到情境支撐、理情相融,操作外化、理行相隨,直觀呈現、理形相依,表征轉化、理型相聯,練習強化、理用相促。
關鍵詞 小學數學教學 算理理解 路徑探討
眾所周知,算理是計算的理論依據,是解決“為什么這樣算”的客觀規律,為計算提供正確的思維方式;算法是算理指導下的計算規則及邏輯順序,是解決“怎樣計算”的人為規定,它保證正確、快捷地計算。算法和算理是計算教學中相互依存的結合體,輕視算理指導、算理理解淺顯的計算教學是不完整的教學。那么,計算教學中如何指導和幫助學生清晰理解算理,實現“循理入法,以理馭法”呢?筆者擬結合教學實踐作簡要探討(案例所涉數學教材均為人教版)。
一、情境支撐,理情相融
現行小學數學教材,計算教學多與解決承載現實情境或背景的數學問題相伴生。此類編排,既可利用所學的數量關系列出算式,體會計算學習的現實需要,又可借助現實情境或背景,幫助學生理解并運用四則運算的含義,明晰算理,實現算理與情境的相互融合。如小數乘小數的計算(五年級上冊P5例3)。
例3 給一個長2.4m、寬0.8m的長方形宣傳欄刷油漆,一共需要多少千克油漆?(每平方米需要油漆0.9kg,圖略)
例題教學重點是掌握小數乘小數的豎式計算方法,難點是理解小數乘小數的算理。理解算理時,教師可設計如下環節:
教學實踐表明,小數乘小數的學習,學生感到困難的不是算法掌握,而是對算理的理解和表述,因此教學關鍵在于,教師應提供充分思考、交流的機會,幫助學生合理解釋計算過程。因此教師應把引導學生分析下面的推理圖,從積和因數的關系出發,完整敘述整個推理過程作為教學重心。
如此安排,既可明確小數乘小數的算理,又為后續自主歸納小數乘小數的算法做好鋪墊。
二、操作外化,理行相隨
操作是學生建構數學認知、形成數學能力的過程,它能使抽象的數學知識具體化,枯燥的文字敘述變成看得見、摸得著的活動,使學習過程變得有趣、快樂,富有思維內涵,有助于學生對所學知識的理解與把握。教師精心設計操作活動,讓學生在活動中有所發現、有所感悟,有助于學生理解較復雜的算理。如分數除以整數的計算(六年級上冊P30例1)。
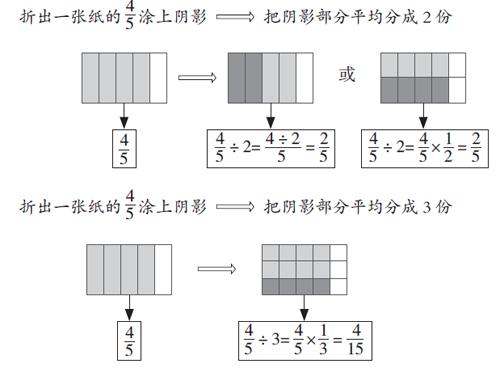
例1把一張紙的平均分成2份,每份是這張紙的幾分之幾?自己試著折一折,算一算。
如果把一張紙的平均分3份,每份是這張紙的幾分之幾?
分數除以整數的算法,是分數除法的基礎,根據分數意義和操作活動溝通分數除以整數與分數乘法的聯系,既是理解算理的關鍵,也是歸納算法的關鍵。教學時,教師指導學生按下面步驟動手操作:
上述操作過程,教師有意識地引導學生將“圖”和“式”對照起來分析、說理,幫助學生建立圖形語言和數字語言的聯系,有效降低學生對分數除以整數算理的理解難度。
三、直觀呈現,理形相依
小學生思維發展處于以直觀形象思維為主向以抽象邏輯思維為主的過渡期,學習數學知識一般遵循具體感知→形成表象→抽象概括的規律,仍需要直觀形象的支持。直觀手段能使其思維在感性認識的基礎上參與認知過程,及時將感性認識上升為理性認識。因此,小學數學教材的編排中大量呈現點子圖、小棒、方格圖、立體圖、計數器等結構化直觀圖,借助直觀把復雜數學問題變得簡明形象,為幫助學生理解算理提供支撐。如被除數各位上的數都能被整除的除法(三年級上冊P15例1)。
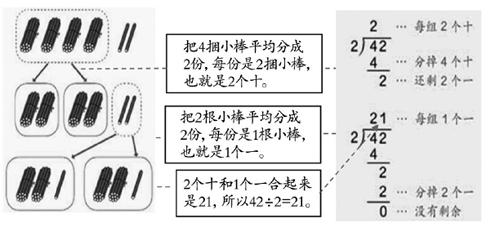
三年級平均每班種多少棵?
教學時,教師先引導學生觀察主題圖,明確解決“三年級平均每班種多少棵?”可列式42÷2計算。再借助課件直觀呈現平均分及豎式計算過程,在豎式邊給出每一步計算中各個數的含義,幫助學生理解算理,掌握除的順序和豎式的寫法。
上述過程中,學生能直觀發現每一步分的結果與豎式中每一部分結果的位置值的對應關系,有效突破一位數除兩位數的教學難點,使算理得到進一步抽象,最后達到脫離直觀算理,掌握算法的預期效果。
四、表征轉化,理型相聯
小學生對數學知識的表征一般分為動作表征、圖像表征和符號表征,學生理解算理的最終成果表現為根據題意和數量關系列出算式,用文字符號予以呈現。教學中,教師應設法幫助學生建立算理的多元表征,培養根據需要與情境在各種表征方式之間做出多元、多向聯結與轉化的能力,加深學生對算理的理解。如20以內的退位減法(第1課時)(一年級下冊P10例1)。
教學中教師引導學生從情境中收集信息,列出算式后,借助學具感悟多種計算方法,重點通過課件直觀演示、理解“破十法”算理。
最后,聯系演示過程,用算式表示“破十法”的算理:
上述安排,教師把具體的操作過程和抽象的計算過程對應起來,引導學生將多種表征方式相互結合并進行有效轉化,幫助學生理解算理和掌握“破十法”,也為學生脫離實物,通過思考算出得數打下了基礎。
五、練習強化,理用相促
練習既是教學效果的檢驗工具,也是學生掌握知識、形成技能、培養能力的有效途徑。計算教學中的練習,既能檢測算法掌握狀況、算法運用能力,又能檢測算理理解程度,促進學生對數學知識的掌握和轉化進程。如兩位數乘兩位數的筆算例1補充設計練習題:
1.想一想,填一填。
設計意圖:觀察思考,明確豎式每一步計算的含義,理解豎式計算算理。
2.下面計算對嗎?對的畫“√”,錯的畫“×”,說一說錯在哪里并改正。
設計意圖:以判斷改錯的形式,選取典型錯例,分析說理,明確豎式每一步計算所對應的位置值,既鞏固算理,又檢驗算法的掌握狀況。
3.把下面算式補充完整。
32×3+32×40=(? ?)×(? ?)
11×8+11×10=(? ?)×(? ?)
設計意圖:從逆向思考的角度,加深學生對算理的理解。
總之,算理學習對計算教學有著特殊的意義,它是計算教學中邏輯思維的運用和體現,是數學理性精神的體現,更是計算以及計算中思維方法能夠靈活遷移的基礎。教師要認識算理的本質,依據小學生的數學認知規律、思維特點設計教學,關注多元表征的運用和轉化,有效幫助學生理解算理,從而提高計算能力。
[責任編輯:陳國慶]

