一維圣維南方程差分數值算法中稀疏矩陣求解方法比較及優選研究

王浩驊，管光華*，肖昌誠,2

·區域農業水管理·

一維圣維南方程差分數值算法中稀疏矩陣求解方法比較及優選研究

王浩驊1，管光華1*，肖昌誠1,2

（1.武漢大學 水資源與水電工程科學國家重點實驗室，武漢 430072；2.中國電建集團 華東勘測設計研究院有限公司，杭州 310014）

【】尋找高效、穩定的大型稀疏線性方程組求解算法以提高圣維南方程組求解速度。歸納了4種基于四點偏心格式的圣維南方程組求解算法并加以改進，并通過仿真試驗，對比了不同算法的計算效率。計算斷面數較少時（小于500），所有方法的運算時間基本一致；當計算斷面數較大時（大于500），4種算法的速度較傳統算法有了一定的提高，在計算斷面數為1 520時，4種算法的計算速度是傳統算法的4倍，在計算斷面數為3040時，計算速度更是達到了10倍以上。改進后的高斯消元法和 PM 算法在計算斷面數較大時計算速度較快，計算效率較高。該方法可應用于MPC控制、LQR控制等渠系自動化控制技術中，以提高仿真程序運算速度。

明渠一維非恒定流；圣維南方程組；大型稀疏矩陣；單個斷面運算時間

0 引 言

【研究意義】為緩解水資源短缺，我國建立了許多大型調水工程，由于其調水距離長、輸送水量大、沿線過水建筑物眾多，控制和調度過程十分復雜，渠道在運行調度過程中不可避免地會出現非恒定流，而圣維南方程組是用來描述和求解非恒定流的重要途徑。自圣維南方程組提出以來，通過長期的研究和實踐已趨于完善[1]。隨著大型調水工程的建設以及運行調度和控制過程的復雜化，如南水北調工程[2]、東深供水工程[3]、引黃濟青工程[4]等，明渠一維非恒定流的求解過程要求更高，原有圣維南方程組的求解方法已經滿足不了計算量和計算速度的要求。提高圣維南方程組的計算速度，有利于推進渠道運行調控的發展和推廣圣維南方程組在其他工程領域的應用。【研究進展】目前對圣維南方程組求解方法的探討較多，國內方面，陳大宏等[5]提出的DORA 算法、王泗遠等[6]提出的不同淺水理論的數值計算方法為圣維南方程組的求解提供了不同的思路，而李文豐等[7]對具線性耗散摩阻力的 Cauchy 問題進的研究、聶大勇等[8]對具張弛項的圣維南方程組的弱解的研究豐富了圣維南方程組的應用范圍。國外方面，Isaacson等[9]率先提出了顯式和隱式的離散方法，為Preissmann 提出其經典的四點差分隱格式創造了前提條件。此后，Fread等[10]提出的壓縮存貯消元法、Liggett等[11]提出的雙追趕法使圣維南方程組的求解方法更加豐富。在求解大型稀疏矩陣的算法優化方面，鄭經緯等[12]提出的基于CUDA的PCG算法大大提升了稀疏矩陣的計算效率，而潘少華等[13]為探究低秩稀疏矩陣優化問題提出了凸松弛和因子分解法，為低秩稀疏矩陣的求解提供了一種思路。目前，稀疏矩陣的求解存在的主要問題有：①如何平衡好大型稀疏矩陣的求解速度與其計算結果的收斂性、精度仍是稀疏矩陣求解的主要問題，即加快求解速度的同時保證必要的收斂和精度，使結果可用；②大型稀疏矩陣元素較少，其對應的方程組易呈病態，現有的矩陣壓縮存儲效率有待提高，預處理方法和優化模型算法有待改進；③作為大型復雜稀疏矩陣，圣維南方程組的求解時間往往過長，如何利用并行計算技術進行圣維南方程組的算法研究以提高計算速度顯得愈發重要。【切入點】圣維南方程組的求解速度和求解算法仍需改進，提升求解速度。【擬解決的關鍵問題】本文為尋找高效、穩定的大型稀疏線性方程組的求解算法以提高圣維南方程組求解速度，歸納了并優化了4種基于四點偏心格式的圣維南方程組求解算法，分別是追趕法（chase）、循環遞減算法（CR）、高斯消元法（GE）以及劃分算法（PM）。同時，還比較了不同求解算法的計算量，并通過仿真實驗，對比了不同算法的計算效率。

1 明渠一維非恒定流及其數值解法

1.1 明渠一維非恒定流模型

圣維南方程組由反映質量守恒定律的連續性方程和反映動量守恒定律的運動方程組成。

1）連續性方程

根據質量守恒，流體系統的質量隨時間的變化率為零，并運用輸出方程，并考慮旁側入流，則一維明渠非恒定漸變流的連續性微分方程[14]為：

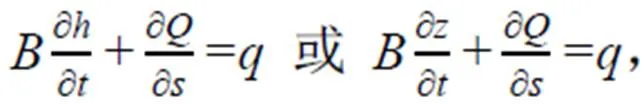
式中：為水面寬（m）；為水位（m）；為時間（s）；為流量（m3/s）；為水深（m）；為斷面的距離坐標（m）；為旁側入流量（m3/(s·m)）。

2）運動方程

對于明渠的非恒定漸變流，通常取在水面，水面相對壓強為0，考慮到流量和流速的關系，一維明渠非恒定漸變流的運動微分方程[14]為：

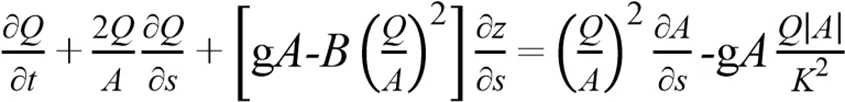
式中：為水面寬（m）；為水位（m）；為時間（s）；為流量（m3/s）；為斷面的距離坐標（m）；g為重力加速度（m/s2）；為過水斷面面積（m2）；為水流沿軸線方向的流速（m/s）。

1.2 有限差分法

有限差分法是求解圣維南方程組常用的數值計算方法之一。有限差分法又可分為顯式差分法和隱式差分法，隱式差分法的基本思想是直接求解由內斷面方程和邊界方程聯立組成的方程組。在所有隱式差分算法中，應用較多的是四點偏心格式。

四點偏心格式，也稱Preissmann差分格式[15-16]，是針對矩形網格中間某點M將因變量的微分形式轉化為差分形式。在距離步長上M點處于正中心，而在時間步長上，存在一個權重因子，偏向已知時層為，偏向未知時層為1-。

U、D、L、R 4 點的流量可以通過線性差值得到，由此可以得到 M 點流量和水位的差分形式，并代入圣維南方程組，可以得到圣維南方程組的差分方程[14]：

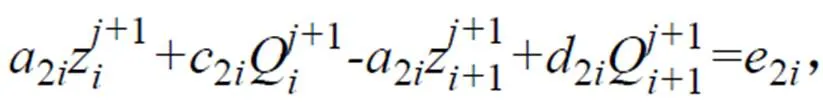
式中：=1,2,……,-1。

在實際計算過程中，若將全河段劃分為個斷面，則有-1個河段，每個斷面有、共2個未知數，共2個未知數。而每個河段可建立2個方程，-1個河段一共可以建立2-2個方程。因此還需要根據上下游邊界的實際情況補充2個方程，構成2個方程才能求解出所有未知數。上下游邊界的條件可統一寫為：

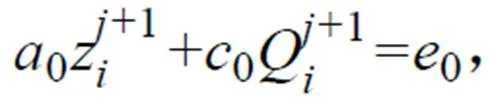
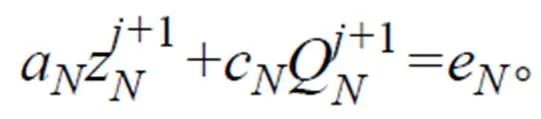
上述的方程組構成了大型稀疏矩陣。該方程組的矩陣形式為：

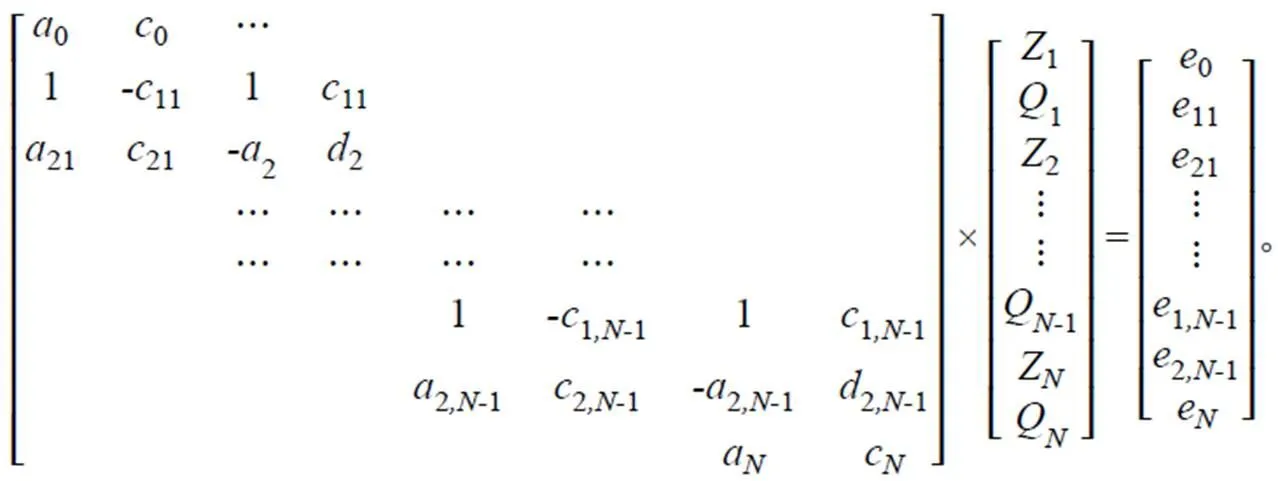
2 稀疏矩陣求解方法

2.1 基于四點偏心格式的算法優化

圣維南方程組的求解需要確定邊界條件，而邊界條件的存在可能使矩陣的某些主對角元素為0，這使得算法求解過程中會出錯，因此需要進行處理。處理的方式有3種：

1)通過初等變換使該位置的元素不為0，這會增加算法的計算量，對于邊界條件較少的矩陣可采用這種方法。

2)將為0的主對角元素用一個極小值來替換，這會引入一定的誤差，其誤差的大小可以通過極小值的大小進行調整。

3)將稀疏矩陣劃分為多個子矩陣，然后通過初等變換進行消元處理，再采用并行技術求解。適用于三對角線性矩陣。

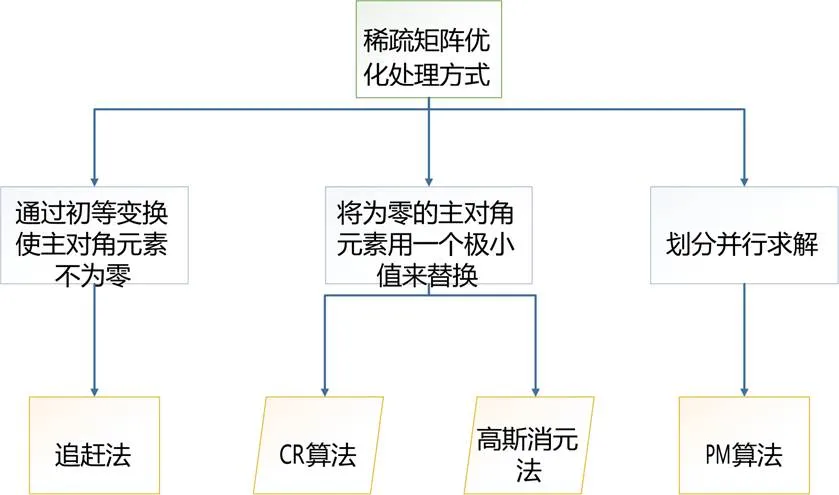
圖1 稀疏矩陣算法優化流程

2.1.1 追趕法（chase）

如式（7）所示，四點偏心格式需要求解的系數矩陣是五對角系數矩陣的一種，首先要通過矩陣間的初等變換將其轉化為三對角線性方程，再進行追趕法的操作，能簡化很多步驟。本文采用的算例的邊界條件較少，因此選擇第一種方式消除主對角的0元素。

2.1.2 循環遞減算法（CR算法）

該算法[17]主要分為2個步驟：向前約化和向后替代。前一步驟為消元，即通過矩陣變化消去所有下標為奇數的變量，保留下標為偶數的變量。此時，大型線性方程組的規模減半，并且消元之后構成新的線性方向組，其系數矩陣仍為原對角形式。按照這個方法執行下去，逐步消元遞減，直到最后只剩下含2個變量的2個方程組時停止消元。對該二元線性方程組進行直接求解，得到2個未知量的解。后一步驟為回代求解，將求得的未知量帶到消元過程的上一個方程組，求出上一方程組的未知量，如此往復求解計算，直到求解得到整個線性方程組的解。

與追趕法求解四點偏心格式相似，CR算法計算前需要將五對角線性方程組轉化為三對角線性方程組。主對角0元素的存在也會影響CR算法的計算過程。通過初等變換使主對角元素為0項進行調整的方法并不適合本算法，因此，本文將為0的主對角元素用一個極小值來替換。

2.1.3 高斯消元法(GE)

以三對角線性方程組為例，其求解思路[18]可分為3個部分：首先是消去系數矩陣對角線以下的元素。將第2個方程乘以2(1)1得到的結果加到第2個方程上，這樣，第2個方程就消去了系數2。同理，之后的每一個方程逐步消元遞減，直到消去對角線以下的所有元素，接著消去系數矩陣對角線以上的元素。如式（8）所示，將第個方程乘以-b-1(a)-1得到的結果加到第-1 個方程上，這樣，第-1個方程就消去了系數b-1。同理，之后的每一個方程逐步消元遞減，直到消去對角線以下的所有元素，線性方程組變成：

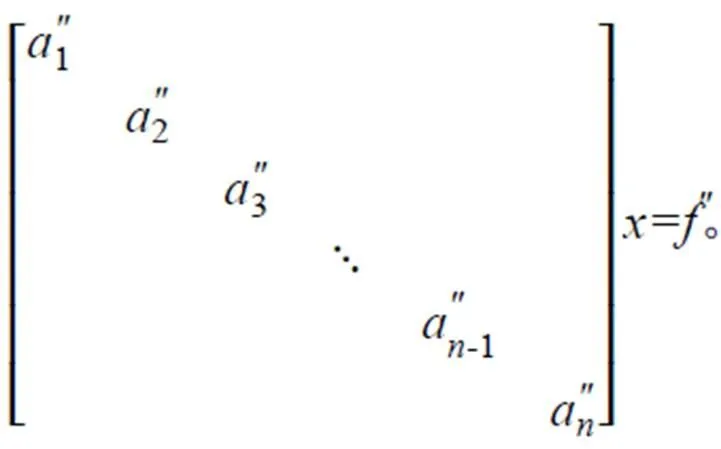
最后求解這一線性方程組，就可以得到原線性方程組的解。與CR算法求解四點偏心格式相似，高斯消元法將為0的主對角元素用一個極小值來替換。

2.1.4 劃分算法（PM算法）

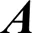
對于矩陣系數為大型稀疏矩陣的方程組，可根據計算機并行的核數，進一步分解為周期塊三對角線性方程組。假設計算機的核數為，可以得到下列方程組：

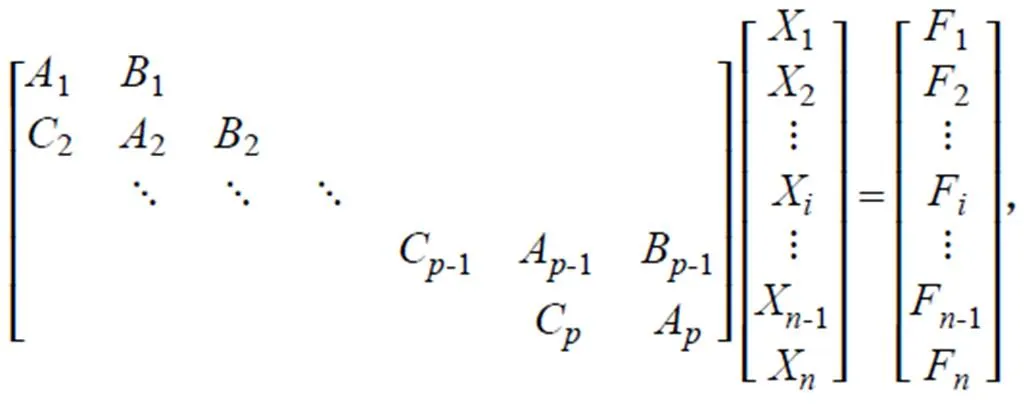
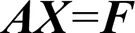
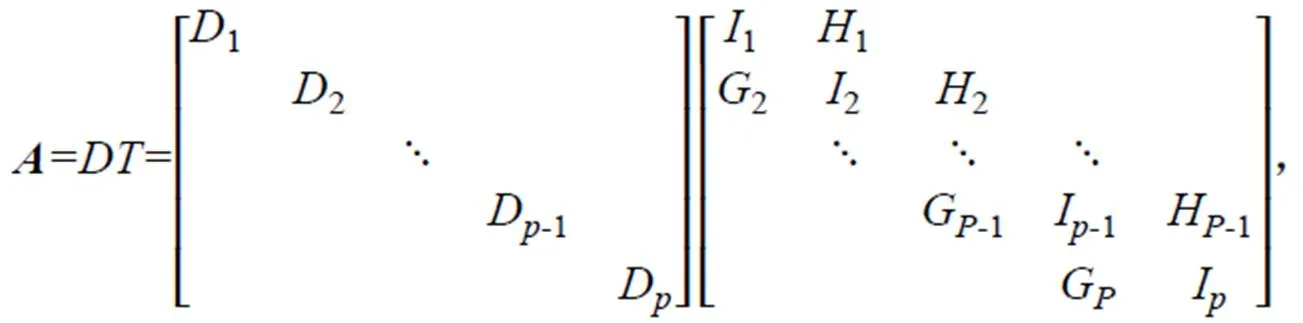
式中：D為m階方陣，I為m階單位方陣，H和G分別為m×m+1和m×m-1矩陣。

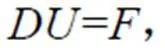
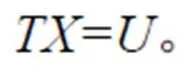
根據式（12）可以得到：

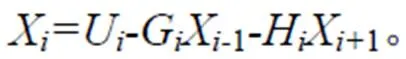
Preissmann 差分格式需要求解的大型稀疏矩陣屬于五對角矩陣，其每一行或每一列最大非0元素的個數為4，屬于元素較少的大型稀疏矩陣。以下是根據該類型矩陣的算法改進。

若B矩陣只有第一列元素非0的情況，則H也只有第一列元素非 0；同理，若C矩陣只有最后一列元素非0的情況，則G也只有最后一列元素非 0。以下就以這種情況為研究對象。

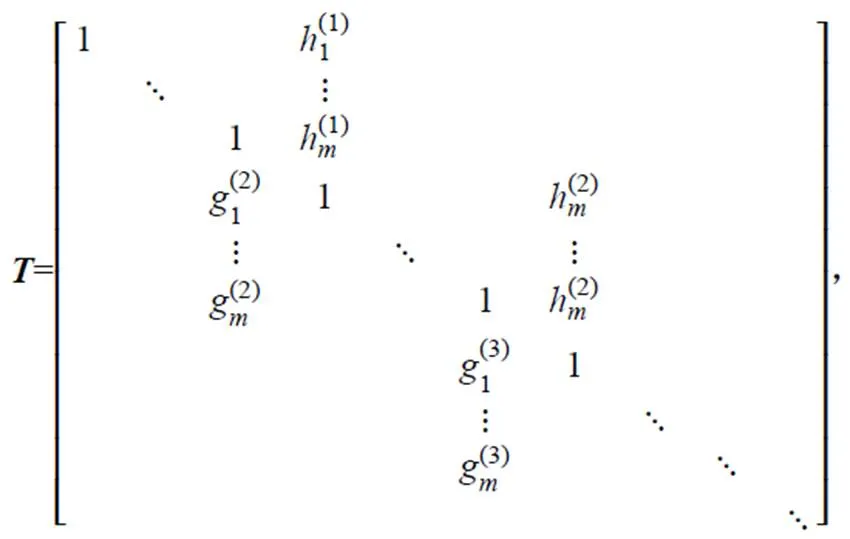
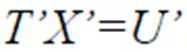
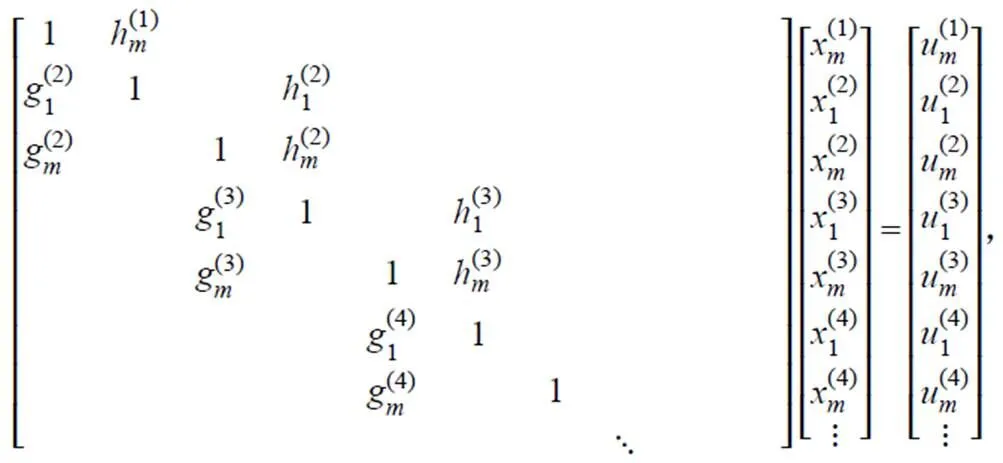
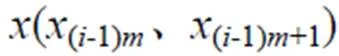
由于H只有第一列元素非0，G只有最后一列元素非2，式(13)可轉化為：

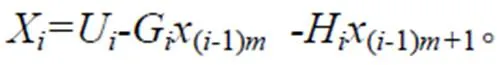
四點偏心格式需要求解的大型稀疏矩陣，可以看作是一種周期塊三對角線性方程組。通過矩陣分塊發現，不同的計算機核數分解產生的B和C矩陣格式也有所差異，可能出現以下2種情況（以B矩陣為例）：

①其分解所得的矩陣H仍只有第一列元素非0，可直接求解；

②其分解所得的矩陣H第一列和第二元素非0，因此在進行矩陣分解前，需要進行矩陣行變換，消去部分項，將B矩陣第二列元素消去。

同理，C矩陣也按上述格式進行矩陣行變換。

2.2 對比分析

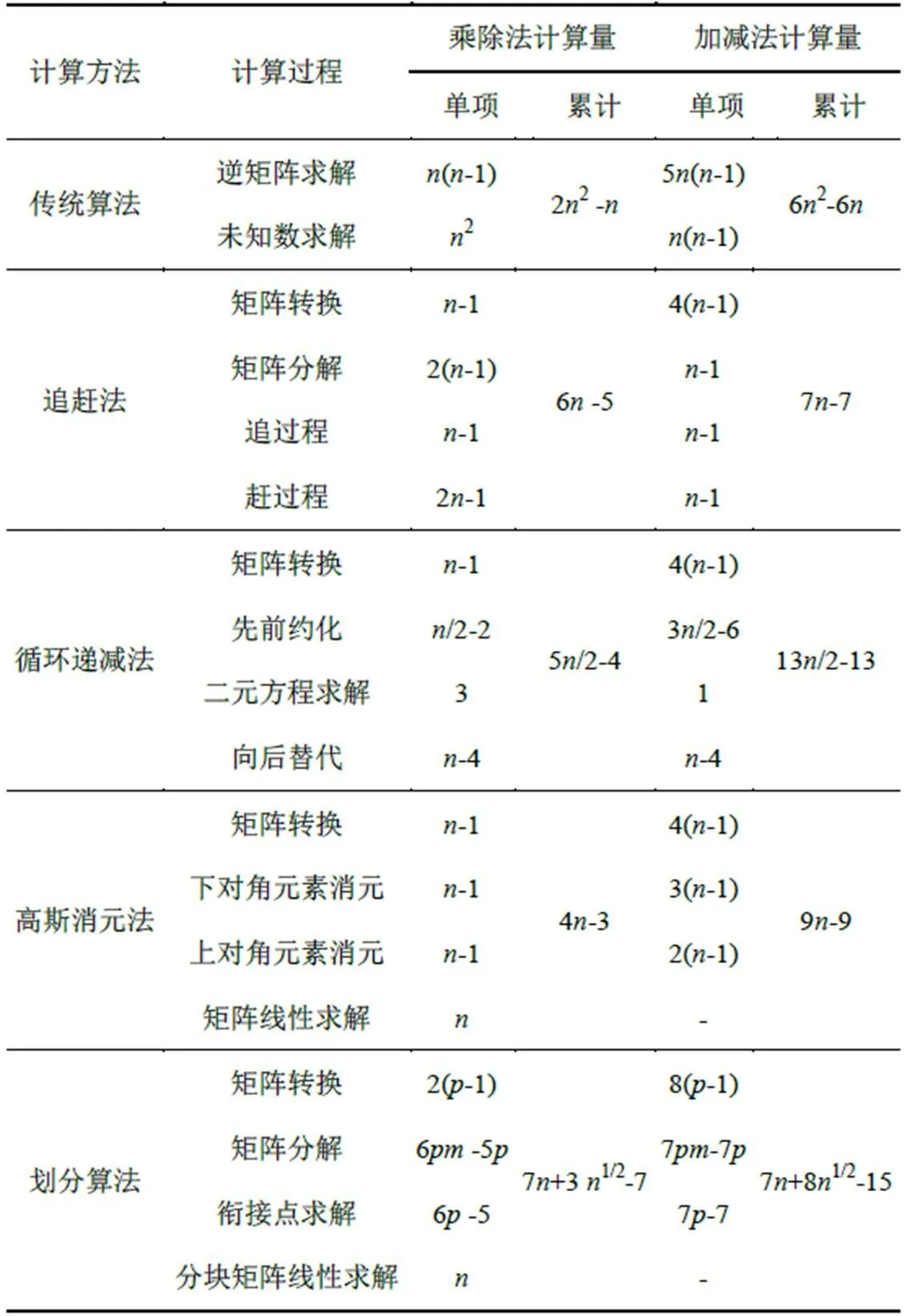
通過對四點偏心格式的不同求解算法的分析，可以得到不同算法的計算量與其系數矩陣階次的關系，其中1/2。在計算機CPU運算過程中，乘法的計算速度比加法慢近10倍。當然，在不同的編譯環境里采用不同的算法，計算速度是不同的[20]，比如C++中，加法一般比乘法快1倍，而劉東[21]提出的Booth 算法的乘法器可以大幅提高乘法的運算速度。因此本文主要比較算法的乘除法計算量。如表1和圖2所示，隨著矩陣階次的增加，傳統算法隨階次的平方增長，而4種算法的計算量呈線性增長，4種算法的計算量較傳統算法大大減少了。當計算階次取值較大時，4種算法中計算量較小的是循環遞減法算法，較大的是劃分算法。

每種算法的運算量的分析是基于理論基礎的，而實際計算過程中，其數據傳輸過程和計算階次也會對運算時間產生較大的影響。因此確定每種算法的計算速度還需具體實驗進行驗證。

表1 5種算法的計算量

Table 1 The amount of calculation of five algorithms

3 算例驗證及結果分析

3.1 仿真渠段

漳河灌區以漳河水庫為主要水源，是典型的“長藤結瓜”灌溉系統。灌區渠系分支眾多，在整個灌區面積上形成了龐大復雜的灌溉渠網系統。灌區內有較多的渠道及渠系水工建筑物，是我國典型的綜合型灌區。探索如何在這種龐大復雜的渠網系統中進行高效的運行調度顯得至關重要，這也是本文仿真的目的之一。本文選取湖北省漳河灌區三干渠三分干部分渠段2004年8月21日的數據進行仿真研究。該渠段中渠系建筑物眾多，包括大量的農耕橋、涵閘以及取水口等，為了仿真和計算方便，在建模過程中做了相應的簡化：為這些渠系附屬建筑物設置相應的水頭損失系數，將其視為對應節點的水頭損失。簡化后渠段的幾何參數和水力特性見圖3和表2。其中渠首閘的閘門參數為：閘門寬度4m，閘門流量系數0.83，閘門最大開度3m。

仿真的邊界條件和初始條件為：①邊界條件：給定上游、下游流量邊界。②初始條件：等體積運行，通過設計水深求各渠段體積，反算各渠段初始下游水深，得到初始水面線。

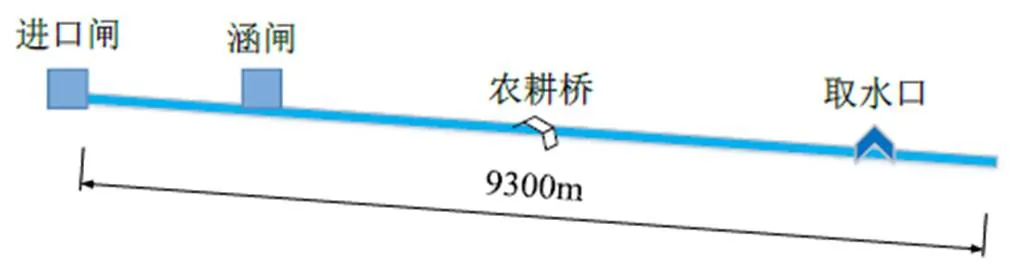
圖3 仿真渠段示意

表2 仿真渠池的幾何參數及水力特性

Table 2 Geometric parameters and hydraulic characteristics of simulation canals

3.2 算例設計

為了說明以上多種大型稀疏矩陣求解方法的計算速度，設計以下試驗：

1）運算平臺：Windows7 系統 Microsoft Visual C++ 2013 (C)。

2）運算環境：Matlab 程序包[22]。

3）計算斷面數：分別為190、380、760、1 520、3 040、4 560、6 080。

4）渠道仿真參數：仿真時間48h；時間步長5min，空間步長隨計算斷面數變化。

對于同一渠道的非恒定流分析，計算精度會隨著選取計算斷面數的增加而增加；但并不是計算斷面數越多越好，實際上計算斷面數滿足計算目的要求即可。在邊際效應的作用下，即便斷面數進一步增加，其計算精度并無實質性提高。本文為了簡化算例，僅在計算對象不變的情況下增加斷面數目即為考慮實際工程的規模可能越發巨大。

每次計算過程為整個渠道的非恒定流仿真過程，因此其運算時間不僅包括大型稀疏矩陣的求解，也包括其他部分的算法和數據處理。

為提高實驗數據的準確度，在運行過程中關閉其他后臺程序。同時，每種工況應執行3次，取3次實驗平均值作為該工況的實驗數據。

3.3 仿真計算及結果分析

3.3.1 運算時間

通過上述工況進行實驗，得到5種算法在不同工況下的運算時間，如表3及圖4所示。

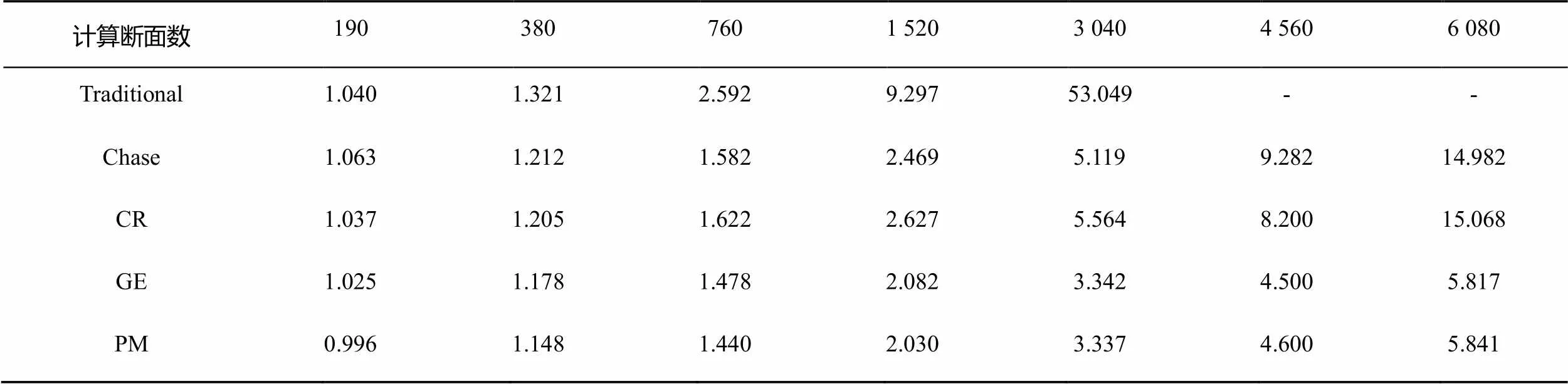
表3 5 種算法在不同計算斷面下的運算時間

注 計算斷面數大于3 040時，采用傳統算法計算時內存不足，故無數據。

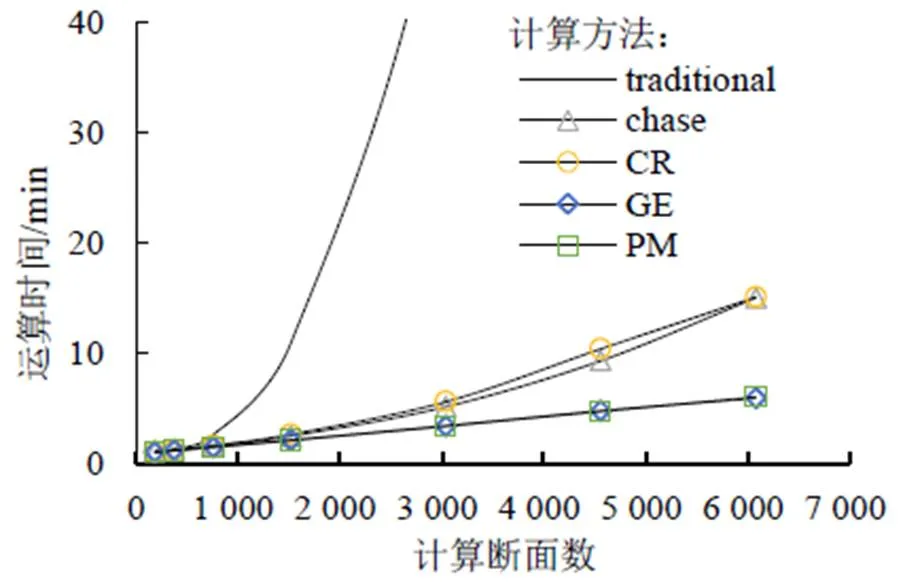
圖4 5 種算法運算時間與運算斷面數的關系圖

3.3.2 單個斷面運算時間

為了更直觀地反映5種算法的計算效率，即運算時間與計算斷面數的關系，本文引入單個斷面運算時間單：

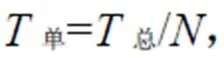
式中：單為單個斷面運算時間（s）；總為總運算時間（s）；計算斷面數。

由圖4及圖5可知，計算斷面數較少時（小于500），所有方法的運算時間基本一致，說明求解大型稀疏矩陣的時間占整個非恒定流問題的很小一部分，因此矩陣求解算法的優劣無法體現。當計算斷面數較大時（大于500），4種算法的速度較傳統算法有了一定的提高，在計算斷面數為1 520時，4 種算法的計算速度是傳統算法的4倍，在計算斷面數為3 040時，計算速度更是達到了10倍以上。傳統算法的單隨斷面數的增加而呈指數型增長，而其他4種算法的單隨著計算斷面的增加而減少，然后趨于穩定；其原因在于傳統算法計算過程中未忽略0元素的計算，隨著計算斷面數的增大，其計算量呈指數型增長；其他4種算法忽略了大量0元素，只計算非0元素，計算量大大減少。

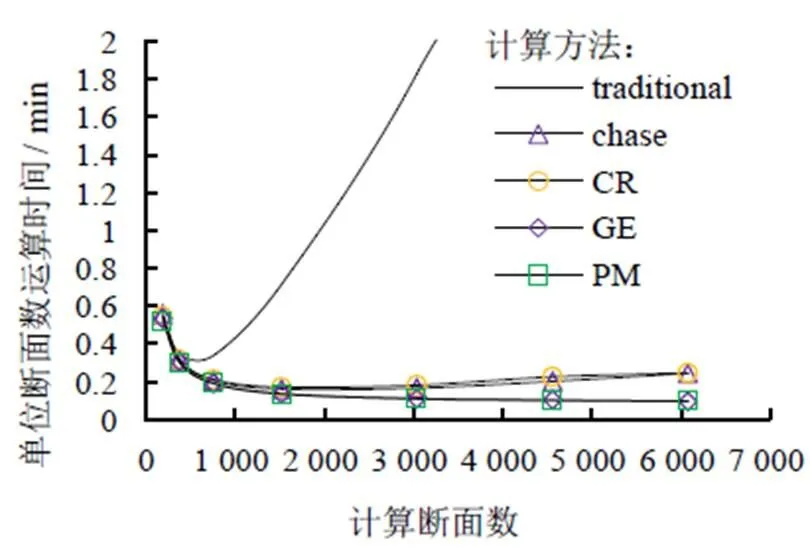
圖 5 5 種算法運算的單個斷面運算時間與運算斷面的關系

3.3.3 誤差分析

本文將4種算法的結果與傳統算法進行誤差對比。為了進行定量比較，本文選取渠道非恒定流計算過程的各個斷面的最終水位作為比較值，分別計算4種算法與傳統方法的水位之間的水位差值，并取其平均值作為絕對誤差進行分析。

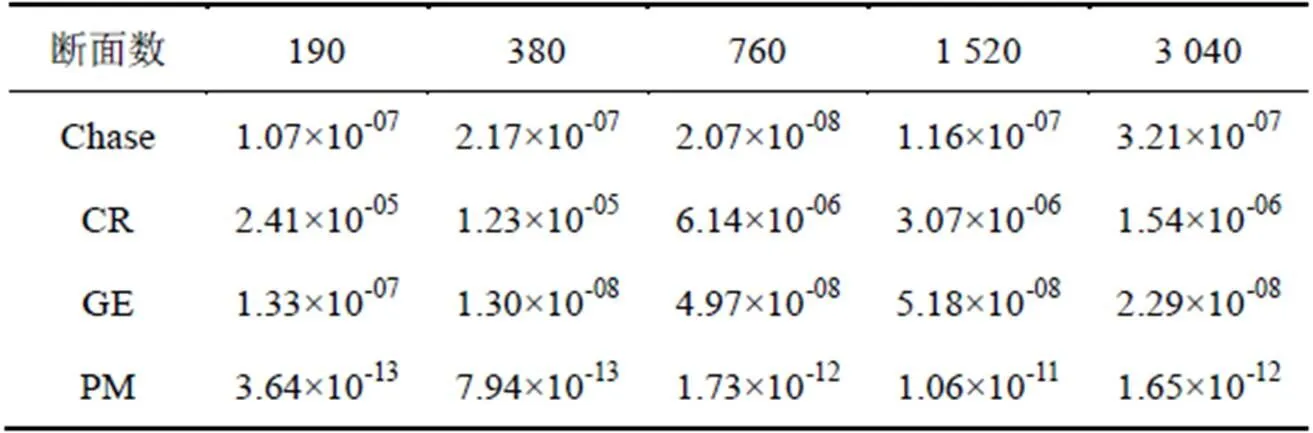
由表4和圖7可知，4種算法的誤差都較小，數量級均在-5以下，當斷面較大時，PM算法和GE算法計算速度更快，誤差更小。其中算法誤差最小的是PM算法，算法誤差最大的是CR算法。這是因為PM算法是通過劃分并行來求解，相對其他3種算法而言優化處理過程不存在誤差，所以誤差最小。而CR算法不僅采用了“將為0的主對角元素用一個極小值來替換”的優化處理方法，而且其算法的步驟為消元加迭代的過程，會使誤差反復累積，因此誤差最大。綜上所述，誤差的結果較為合理。

表 4 4種算法的水位絕對誤差平均值

Table 4 Mean absolute water level error of four algorithms m

4 討 論

國內外學者在大型稀疏矩陣問題上做了大量的研究工作，并取得了較好的效果。然而，由于大型稀疏矩陣的復雜性，始終無法平衡好大型稀疏矩陣求解中求解速度與收斂性和精度的矛盾[15]，也無法徹底解決由于主對角0元素導致的病態方程組問題[16]。

基于此，本文在Preissmann 差分格式研究的基礎上，提出了4種優化算法并進行了仿真驗證。結果表明：①5種算法單個斷面運算時間的差異體現了大型稀疏矩陣中0元素對計算量的巨大影響。通過正確的方式處理0元素，可以使計算量呈指數級下降。當計算斷面數為1 520時，4種算法的計算速度是傳統算法的4倍；當計算斷面數為3 040時，新算法與傳統算法的計算速度差距達到了10倍以上。②不同算法的優化處理方式差異是導致了其絕對誤差產生差異的內因。PM算法是通過劃分并行來求解，相對其他3種算法而言優化處理過程不存在誤差，所以誤差最小。而CR算法不僅采用了“將為0的主對角元素用一個極小值來替換”的優化處理方法，而且其算法的步驟為消元加迭代的過程，會使誤差反復累積，因此誤差最大，但其誤差均不超過-5數量級。

未來在對圣維南方程組的求解研究應加強以下幾個方面：①在優化圣維南方程組的算法過程中，應結合實際問題來考慮合理的誤差允許值。目前的許多求解算法沒有結合實際的問題背景，往往導致其無法很好的運用于解決實際問題。②建立大量的模型試驗來驗證仿真結果。圣維南方程組的求解目的是為了解決實際的水力學問題，仿真結果只有通過大量的模型試驗驗證，才有實際價值。③在圣維南方程組的求解中引入并行計算技術。目前已有很多關于并行計算技術在大型稀疏矩陣中應用的研究，但并行計算技術在圣維南方程組中的應用的相關研究仍較少。并行計算能夠有效加快運算速度，提高運算能力，求解更大規模的問題。但其同時有其局限性：求解的問題具有一定的并行度且需要合理的并行算法。因此，并行計算技術在圣維南方程組中的應用也需要進一步研究。

本文的結果對提高大型渠道非恒定流仿真的運算速度具有參考價值，其方法可應用于MPC控制、LQR控制等渠系自動化控制技術中，以提高仿真程序運算速度。

5 結 論

1)當計算斷面較多時，4種算法的計算速度優勢得以體現，高斯消元法和PM算法的計算速度優勢相對更大，且計算速度的差距隨著斷面數的增加不斷擴大。

2)當計算斷面數小于500左右時，5 種算法的計算速度基本一致；當斷面數在500到1 500范圍內，可選擇除傳統算法以外的其他4種算法進行計算；當斷面數大于1 500時，選擇高斯消元法和PM算法為佳。相較高斯消元法，PM算法編程復雜，但易實現并行計算。

3）4種算法的絕對誤差都較小，最大絕對誤差平均值也都不超過-5數量級，完全在可接受范圍之內，并且其誤差值并不會隨著計算斷面的增加而增大。

4）在計算斷面較大時，推薦采用PM算法與高斯消元法；當考慮并行計算時，推薦采用PM算法。

[1] 聶大勇.一維圣維南方程組整體經典解[D].鄭州:華北水利水電學院,2007.

NIE Dayong. Global Classical Solution of One-dimensionalSaint-Venant Equations [D]. Zhengzhou: North China University ofWater Resources and Electric Power, 2007.

[2] 黃會勇, 閆弈博, 高漢,等. 南水北調中線總干渠運行調度反饋控制方式研究[J]. 人民長江, 2014, 45(6): 56-59.

HUANG Huiyong, YAN Yibo, GAO Han, et al. Study of feedback control on operation and dispatch of main canal of middle route project of south-to-north water diversion[J]. Yangtze River, 2014, 45(6): 56-59.

[3] 曾庚運. 東深供水改造工程全線供水調度與管理自動化[J]. 中國農村水利水電, 2003(9): 1-5.

ZENG Gengyun. All-line water supply dispatching and the management automation in Dongshen water supply improvement project[J]. China Rural Water and Hydropower, 2003(9): 1-5.

[4] 韓延成, 趙洪麗, 張燁,等. 引黃濟青工程調度運行自動控制系統研究[A]. 宮崇楠, 張金麗. 山東水利學會第十屆優秀學術論文集[C]. 濟南: 山東省科學技術協會, 2005.

HAN Yancheng, ZHAO Hongli, ZHANG Ye, et al. Research on the automatic control system for dispatching operation of the Yellow River Diversion Project[A]. Gong Chongnan, Zhang Jinli. The 10th Excellent Academic Papers of Shandong Water Conservancy Society[C]. Jinan: Shandong Association for Science and Technology, 2005.

[5] 陳大宏, 藍霄峰, 楊小亭. 求解圣維南方程組的DORA算法[J]. 武漢大學學報(工學版), 2005, 38(5): 41-44.

CHEN Dahong, LAN Xiaofeng, YANG Xiaoting. DORA approach for solution of the Saint-Venant equations[J]. Engineering Journal of Wuhan University, 2005, 38(5): 41-44.

[6] 王泗遠, 郭澤慶, 王高亞. 明渠非恒定流問題的數值計算方法: 以圣? 維南方程組的數值計算方法為例[J]. 中國新技術新產品, 2011 (10): 7.

WANG Siyuan, GUO Zeqing, WANG Gaoya. Numerical calculation method of non-constant flow in open channel: Taking the numerical calculation method of Saint Vinnan equations as an example [J]. China New Technologies and Products, 2011 (10): 7.

[7] 李文豐, 聶大勇. 具線性耗散摩阻力的圣維南方程組Cauchy問題探討[J].黃河水利職業技術學院學報,2013, 25(1): 51-54.

LI Wenfeng, NIE Dayong. Cauchy Problem of Saint Venan Equations with Linear Dissipative Friction[J]. Journal of Yellow River Conservancy Technical Institute, 2013, 25 (1): 51-54.

[8] 聶大勇, 高杰, 陳征. 具張弛項的圣維南方程組的弱解[J]. 應用數學, 2016, 29(2): 381-387.

NIE Dayong, GAO Jie, CHEN Zheng. Weak solutions for saint-venant systems with relaxation[J]. Mathematica Applicata, 2016, 29(2): 381-387.

[9] ISAACSON E, STOKER J J, TROESCH A. Numerical Solution of Flood Prediction and River Regulation Problems[M]. New York: New York University Institute of Mathematical Science, 1956.

[10] FREAD D L, SHEDD R C, SMITH G F, et al. Modernization in the national weather service river and flood program[J]. Weather and Forecasting, 1995, 10(3): 477-484.

[11] LIGGETT J, CUNGE J. Numerical methods of solution of the unsteady flow equations[M]. Fort Collins, Colorado: Water Resources Publications, 1975.

[12] 鄭經緯, 安雪暉, 黃綿松. 基于 CUDA 的大規模稀疏矩陣的 PCG 算法優化[J]. 清華大學學報(自然科學版), 2014, 54(8): 1 006-1 012.

ZHENG Jingwei, AN Xuehui, HUANG Miansong. CUDA-based PCG algorithm optimization for a large sparse matrix[J]. Journal of Tsinghua University (Science and Technology), 2014, 54(8): 1 006-1 012.

[13] 潘少華, 文再文. 低秩稀疏矩陣優化問題的模型與算法[J]. 運籌學學報, 2020, 24(3): 1-26.

PAN Shaohua, WEN Zaiwen. Models and algorithms for low-rank and sparse matrix optimization problems[J]. Operations Research Transactions, 2020, 24(3): 1-26.

[14] 趙昕, 張曉元, 趙明登. 水力學[M]. 北京: 中國電力出版社, 2009.

ZHAO Xin, ZHANG Xiaoyuan, ZHAO Mingdeng. Hydraulics[M]. Beijing: China Electric Power Press, 2009.

[15] 顧峰峰, 倪漢根. 四點時空偏心隱格式的改進求解[J]. 大連理工大學學報, 2007, 47(3): 419-423.

GU Fengfeng, NI Hangen. Two improved calculation methods of Preissmann four-point linear implicit scheme[J]. Journal of Dalian University of Technology, 2007, 47(3): 419-423.

[16] 葛華. Preissmann 四點時空偏心隱格式思想在二維數學模型中應用初探[J]. 科學技術與工程, 2007, 7(1): 91-93.

GE Hua. Application of the preissmann difference scheme to the 2-D model (preliminary study)[J]. Science Technology and Engineering, 2007, 7(1): 91-93.

[17] 唐光平. 基于三對角線性方程組的混合并行算法研究[D]. 長沙: 湖南大學, 2015, 2015.

TANG Guangping. Research on hybrid parallel algorithms based on tridiagonal linear equations [D]. Changsha: Hunan University, 2015.

[18] 彭朝英. 高斯消元法的改進及其在工程上的應用[J]. 邵陽學院學報(自然科學版), 2011, 8(2): 26-30.

PENG Chaoying. Improvement of the Gaussian elimination method and its application in engineering MCU[J]. Journal of Shaoyang University (Science and Technology), 2011, 8(2): 26-30.

[19] 朱成. 五對角線性方程組的并行求解算法的研究[D]. 長沙: 湖南大學, 2016.

ZHU Cheng. Research on Parallel Solving Algorithm of Pentadiagonal Linear Equations [D]. Changsha: Hunan University, 2016.

[20] 羅福強, 馮裕忠, 茹鵬. 計算機組成原理[M]. 北京: 清華大學出版社, 2011.

LUO Fuqiang, FENG Yuzhong, RU Peng. Principles of computer organization[M]. Beijing: Tsinghua University Press, 2011.

[21] 劉東. 采用 Booth 算法的16×16 并行乘法器設計[J]. 現代電子技術, 2003, 26(9): 21-22, 25.

LIU Dong. Design of parallel multiplier for borth algorithm[J]. Modern Electronics Technique, 2003, 26(9): 21-22, 25.

[22] 武漢大學. 輸水渠道系統運行仿真與控制軟件 V1.0: 中國, 2011SR034392[P]. 2011-06-03.

Wuhan University. Simulation and control software for water conveyance system operation V1.0: China, 2011SR034392[P]. 2011-06-03.

[23] BONDARENCO M, GAMAZO P, EZZATTI P. A comparison of various schemes for solving the transport equation in many-core platforms[J]. The Journal of Supercomputing, 2017, 73(1): 469-481.

[24] NAVABPOUR B, OSTAD ALI ASKARI K, ESLAMIAN S, et al. Comparison of solutions of Saint-Venant equations by characteristics and finite difference methods for unsteady flow analysis in open channel[J]. International Journal of Hydrology Science and Technology, 2018, 8(3): 229.

[25] 黃凱, 管光華, 劉大志,等. 串聯渠系 PID 改進積分與微分環節仿真研究[J]. 灌溉排水學報, 2017, 36(2): 1-11.

HUANG Kai, GUAN Guanghua, LIU Dazhi, et al. Simulation for PID controller of modified integral and differential on tandem canal system[J]. Journal of Irrigation and Drainage, 2017, 36(2): 1-11.

[26] 李一鳴, 管光華, 陳琛,等. 渠道糙率影響因素分析及預測模型研究[J]. 灌溉排水學報, 2017, 36(S2): 155-161, 189.

LI Yiming, GUAN Guanghua, CHEN Chen, et al. Analysis of influencing factors of canal roughness and prediction model [J] .Journal of Irrigation and Drainage, 2017, 36 (S2): 155-161, 189.

[27] 張慧, 伍萍輝, 張馨,等. 非垂直拍攝獲取細葉作物覆蓋度優化算法研究[J]. 灌溉排水學報, 2019, 38(9): 55-62.

ZHANG Hui, WU Pinghui, ZHANG Xin, et al. Research on optimization algorithm of fine leaf crop coverage based on non-vertical shooting[J]. Journal of Irrigation and Drainage, 2019, 38(9): 55-62.

Comparison and Optimization of Sparse Matrix Solution Methods in One-dimensional Saint-venant Equation Difference Numerical Algorithm

WANG Haohua1, GUAN Guanghua1, XIAO Changcheng1, 2

(1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China; 2. Power China HuaDong Engineering Corporation, Hangzhou 310014, China)

【】In order to alleviate the shortage of water resources, China has established many water transfer projects. Due to its long water transfer distance, large water delivery volume, and numerous water passing buildings along the line, the control process is very complicated. Unsteady flow will inevitably appear in the channel operation scheduling process, and the Saint-venant equations are an important way to describe and solve the unsteady flow.【】With the construction of large-scale water transfer projects and the complexity of the operation scheduling and control process, the traditional method of solving the sparse matrix of the original Saint-Venant equations has been unable to meet the requirements of calculation volume and calculation speed. In order to find efficient and stable algorithms for solving large and sparse linear equations to improve the speed of solving Saint-Venant equations.【】In this paper, four algorithms for solving Saint-Venant equations based on the four-point eccentric scheme are summarized and improved, and the calculation efficiency of different algorithms is compared through simulation experiments.【】From the simulation results, it can be seen that when the number of calculation sections is small (less than 500), the calculation time of all methods is basically the same; when the number of calculation sections is large (more than 500), the speed of the four algorithms is improved compared with the traditional algorithm.When the number of cross sections is 1 520, the calculation speed of the four algorithms is 4 times that of the traditional algorithm. When the number of cross sections is3040, the calculation speed is more than 10 times.【】The improved GE and PM algorithms have faster calculation speed and higher calculation efficiency when the number of cross sections is larger. The results of this paper have reference value for improving the calculation speed of large channel non-constant flow simulation. The method can be applied to canal system automatic control technology such as MPC control, LQR control point, etc., to improve the running speed of simulation program.

one dimensional unsteady flow in open-channel; Saint-venant equations; large sparse matrices; calculation time of a single section

TV133

A

10.13522/j.cnki.ggps.2020182

1672-3317（2021）03-0116-09

王浩驊, 管光華, 肖昌誠. 一維圣維南方程差分數值算法中稀疏矩陣求解方法比較及優選研究[J]. 灌溉排水學報, 2021, 40(3): 116-124.

WANG Haohua, GUAN Guanghua, XIAO Changcheng. Comparison and Optimization of Sparse Matrix Solution Methods in One-dimensional Saint-venant Equation Difference Numerical Algorithm[J]. Journal of Irrigation and Drainage, 2021, 40(3): 116-124.

2020-03-31

國家自然科學基金項目（51979202，51439006，51009108）；“十三五”國家重點研發項目（2016YFC0401810）

王浩驊（1996-），男，浙江臺州人。碩士研究生，主要從事灌排自動化研究。E-mail: 2290586701@qq.com

管光華（1979-），男，江蘇阜寧人。副教授，碩士生導師，主要從事灌排自動化及量水理論研究。E-mail: GGH@whu.edu.cn

責任編輯：白芳芳