具有Allee 效應的捕食-食餌擴散模型定性分析
李海俠
(寶雞文理學院數學與信息科學學院,寶雞 721013)
1 引言
1931 年Allee 在研究過程中發現群居的生活狀態有利于種群的增長,但是密度太大又會抑制種群的生長甚至會因為資源爭奪而走向滅絕.對于每一個種群來說,必定存在著它獨立的最適合自身生長繁殖的最佳密度,這就是Allee 效應.已有大量的理論和實驗證明,Allee 效應與種群的滅絕密切相關,在很大程度上能增加低密度種群的滅絕風險,尤其對小種群、分散種群、稀有種群以及瀕臨滅絕種群的動力學行為具有非常大的影響.因此,研究具有Allee 效應的生物模型對生物保護具有很重要的意義,近年來受到了生物學家和數學家的很大關注[1-10].
本文在齊次Dirichlet 邊界條件下考慮如下具有B-D 反應函數和Allee 效應捕食-食餌擴散模型
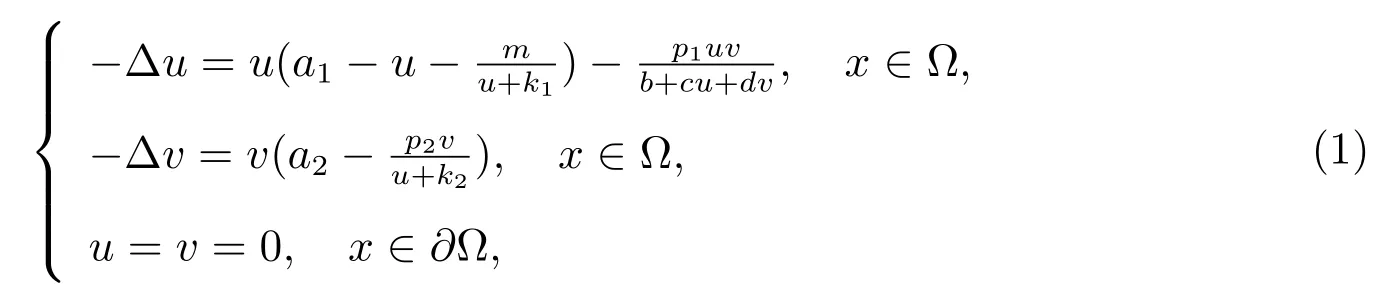
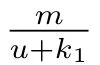
為了得到重要的結論,這節最后我們給出一些預備知識.
-Δψ+q(x)ψ =λψ, x ∈Ω, ψ =0, x ∈?Ω,
則λ1(q)連續依賴q,λ1(q)是簡單的.而且,如果q1≤q2, q1/≡q2,則λ1(q1)<λ1(q2).為了簡單起見,定義λ1(0)為λ1,相應于λ1的主特征函數記為ψ1.
非線性問題
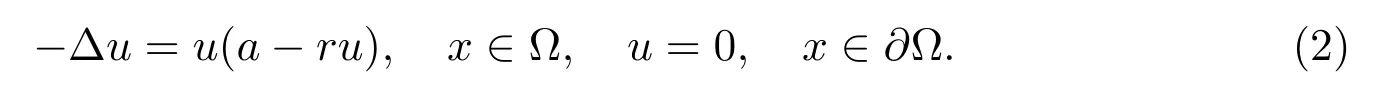
眾所周知,若a >λ1,則(2)存在唯一正解.我們定義唯一正解為θ(a,r).特別地,記θ(a,1)為θa,則θa<a 且θa連續依賴a.
2 正解的存在性、不存在性和唯一性
考慮單物種問題

根據文獻[6]可得如下引理.
引理1[6]系統(1)的任意正解(u,v)有先驗估計
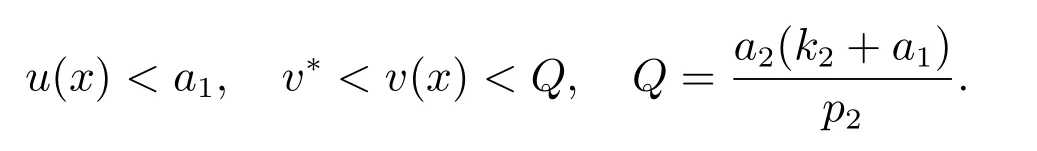
引理2[6]如果系統(1)有正解,則a1>λ1, a2>λ1.
為了計算不動點指數,引入以下記號
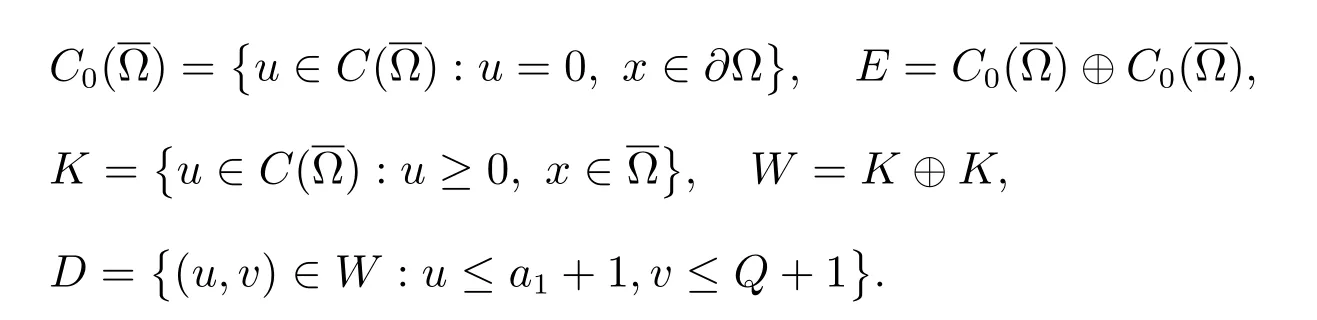
取q 充分大,使得q >max{m/k1+p1/d,a2(a1+k2)/k2}.定義算子A:E →E 為
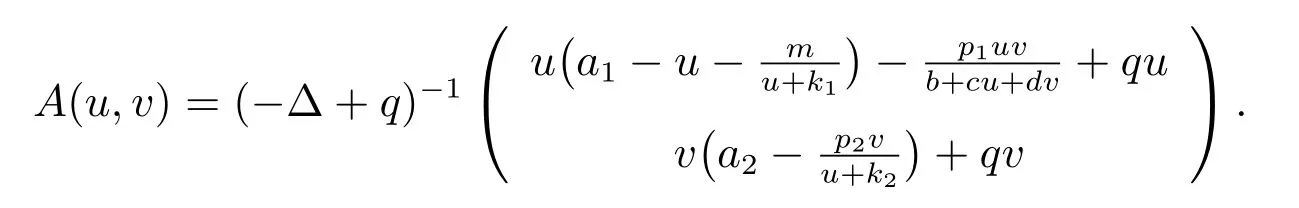

證明 根據已知條件和定理1 可知系統(1)存在正解.采用反證法證明唯一性.假設系統(1)存在兩個不同的正解(u1,v1)和(u2,v2),其中ui>0, vi>0(i = 1,2).由比較原理和引理1 可知u*≤ui≤u*, v*≤vi≤v*,這里u*, v*分別為如下問題的唯一正解
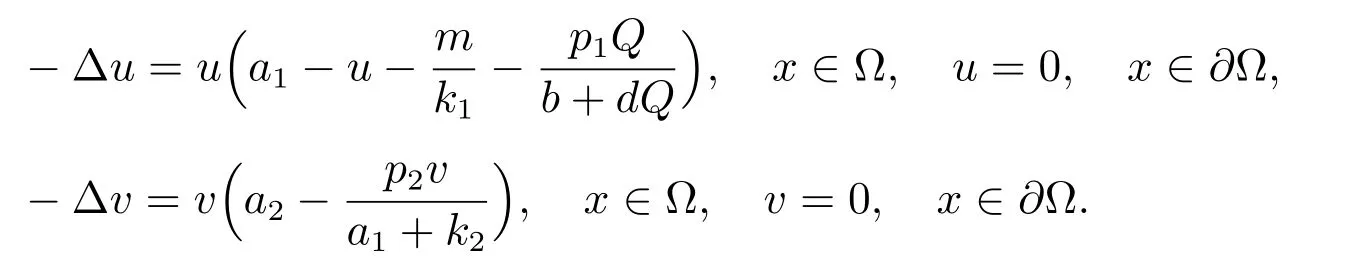
令Φ=u1-u2, Ψ=v1-v2,則
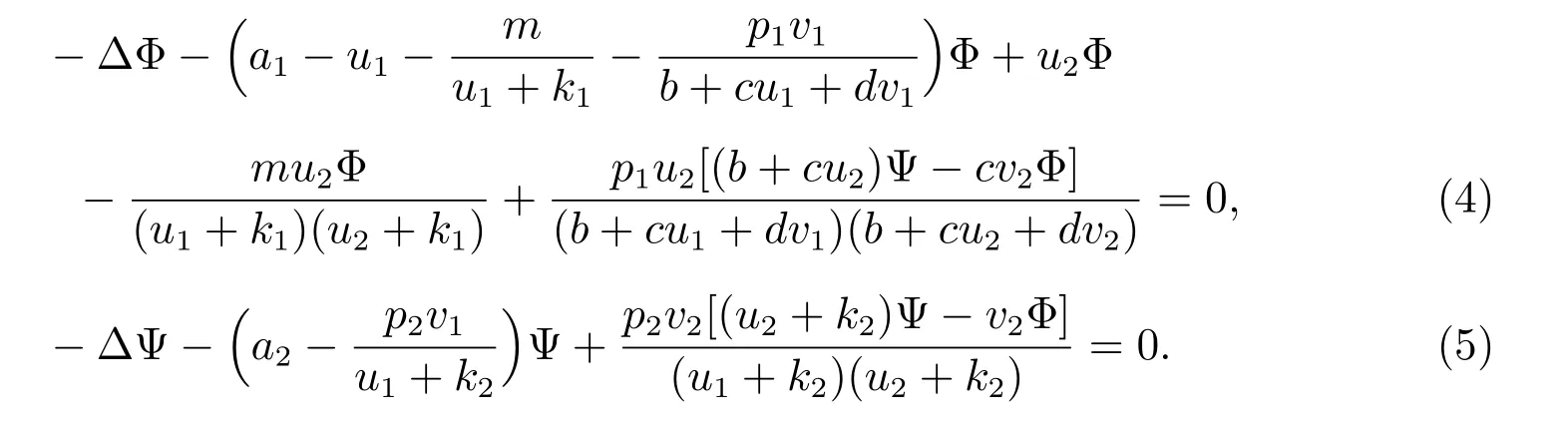
因為(u1,v1)是系統(1)的正解,所以根據特征值的變分原理可知
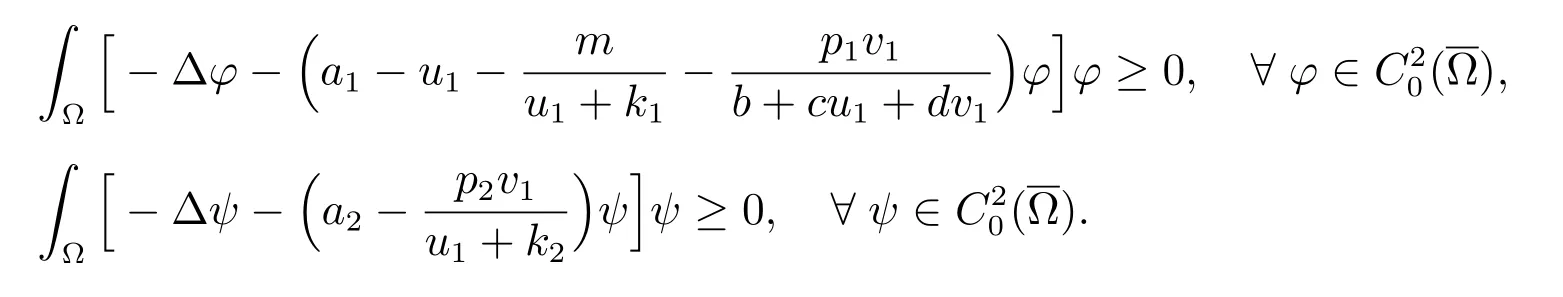
于是,公式(4)表明
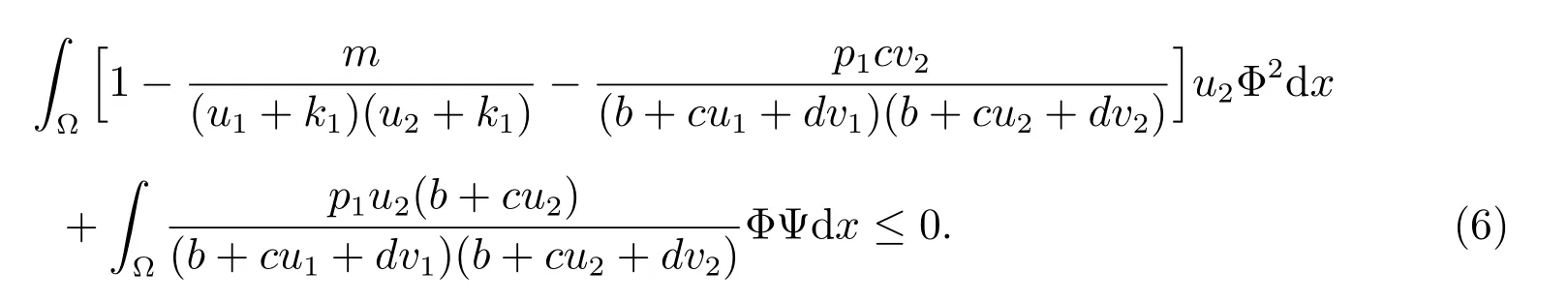
同理,由(5)式有
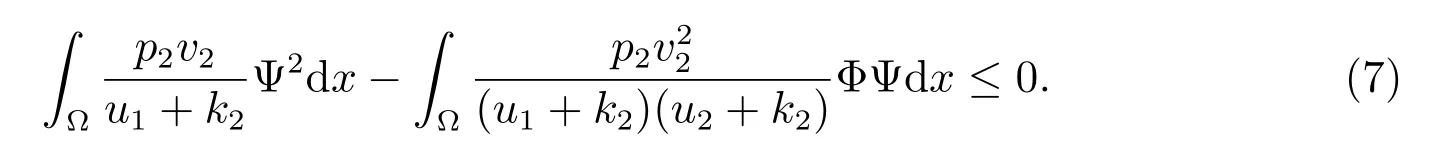
令
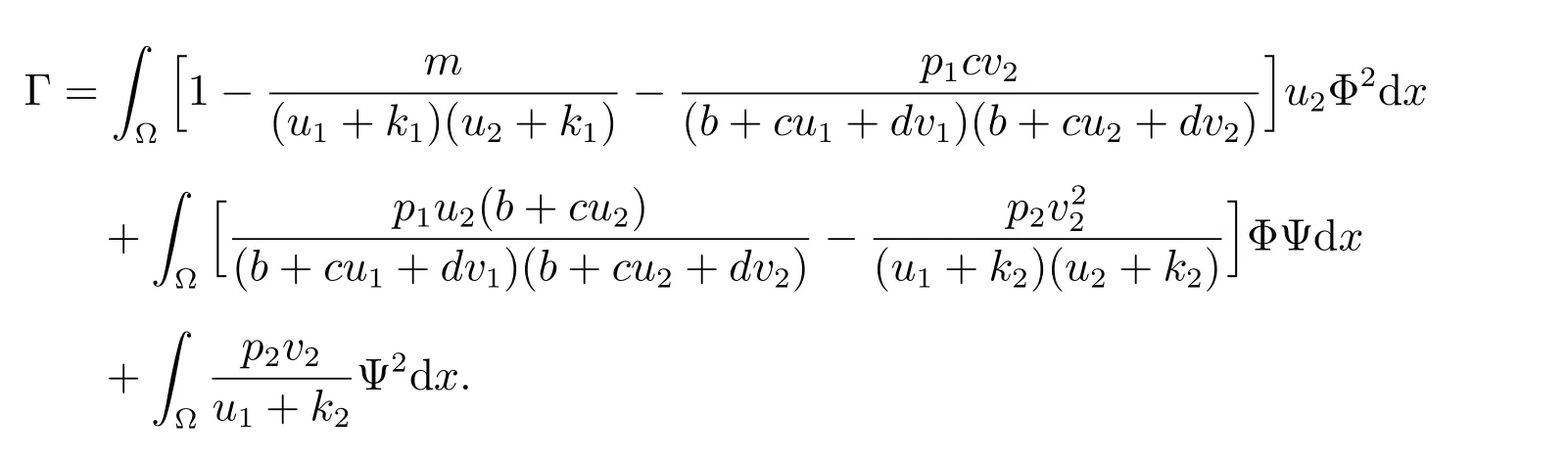
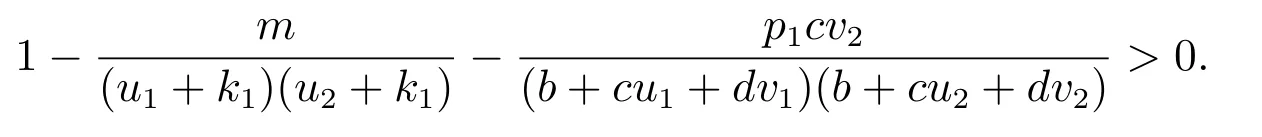
最后,令
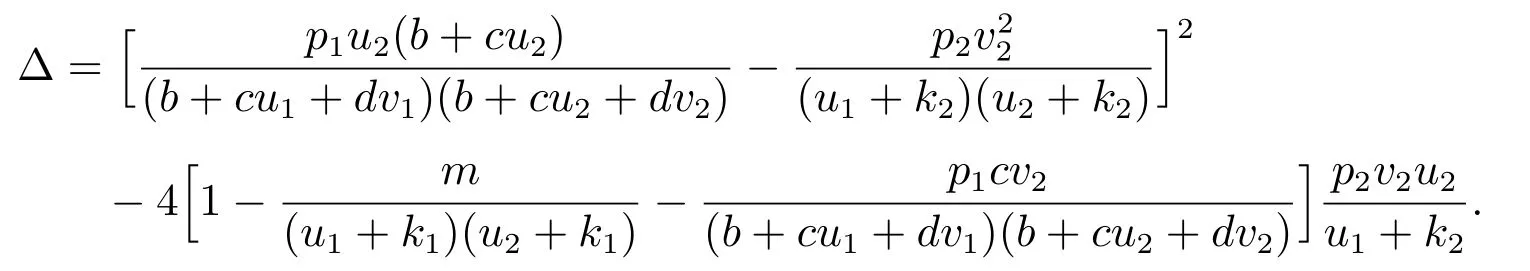
經過計算并結合已知條件可得
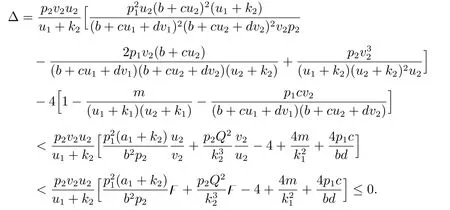
故Γ >0.而式(6)和(7)可知Γ ≤0,矛盾.因此結論成立.
3 正解的確切重數和穩定性
本小節應用擾動理論和不動點指數理論討論參數c →∞時,系統(1)正解的確切重數和穩定性.易看出當c →∞時,系統(1)的正解有兩種類型,即如果(u,v)是系統(1)的任意正解,則對于充分大的c,(u,v)趨于如下問題的正解
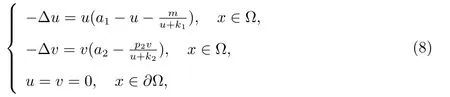
或者(cu,v)趨于如下問題的正解
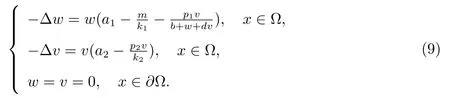
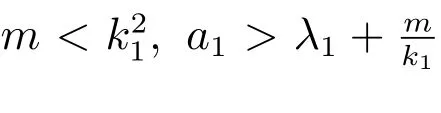
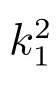
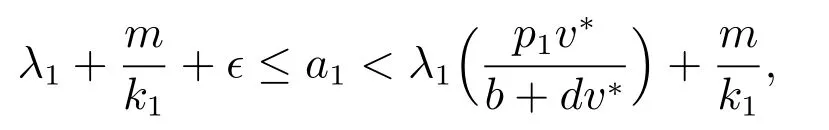
則系統(1)至少存在兩個正解.
如果a2>λ1,則問題(9)等價于如下問題
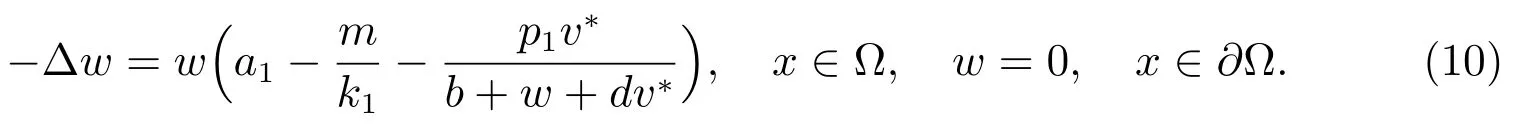
對于問題(10),用類似文獻[11]的證明方法有如下引理.
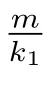
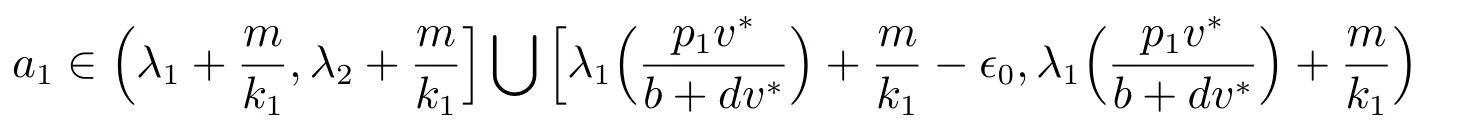
時,(10)的正解(若存在)唯一且非退化.
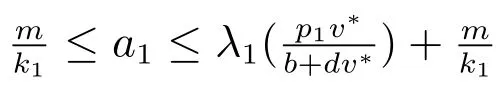
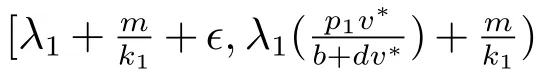
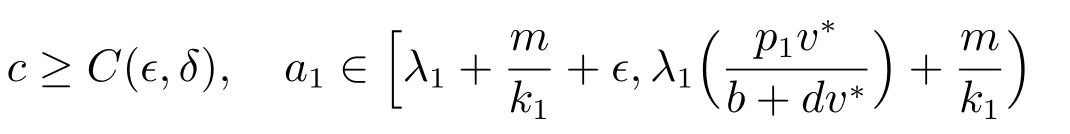
且(u,v)是(1)的正解,則:
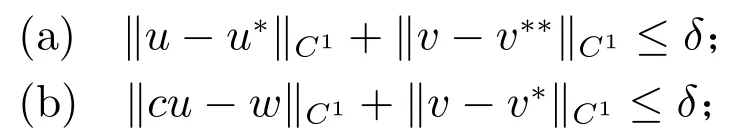
這里w 是(10)的正解,v**為如下問題的正解
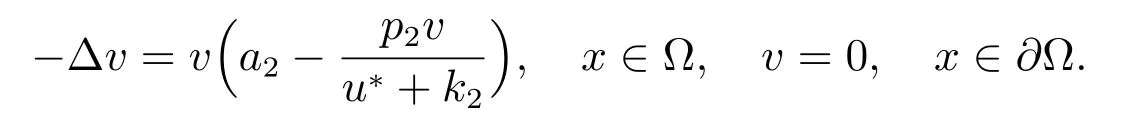
而且,若(a)情形出現,則正解(u,v)非退化且線性穩定.
證明 采用反證法證明.假設存在
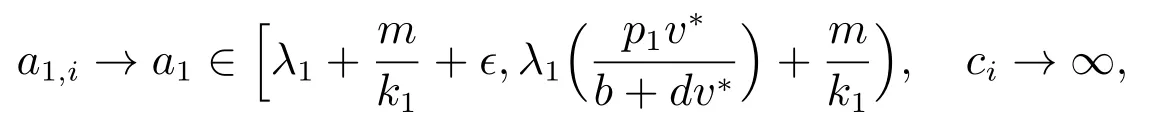
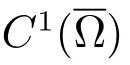
(i) 若ci‖ui‖∞→∞,則當i →∞時,ui→u*.因此vi→0 或vi→v**.而a2>λ1,所以必有vi→v**,即(ui,vi)→(u*,v**).這與假設(ui,vi)遠離(u*,v**)矛盾;
(ii) 若ci‖ui‖∞一致有界,則當i →∞時,ui→0.于是vi→v*.設ciui= wi,則wi滿足
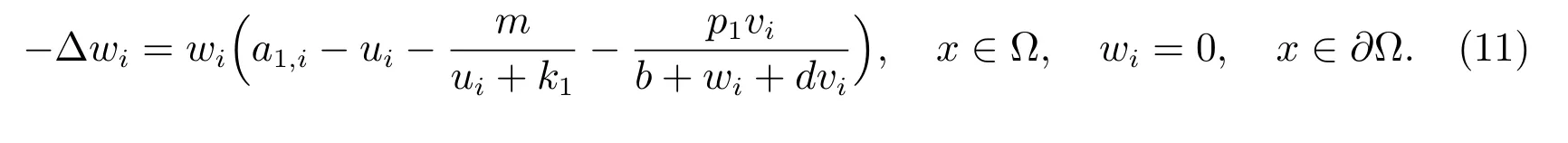

則系統(1)恰好有兩個正解,一個漸近穩定而另一個不穩定,這里?0在引理5 中給出.
證明 根據引理7 分兩步證明.首先證明當c 充分大時,(1)接近(u*,v**)的正解唯一且漸近穩定.引理7 可知系統(1)接近(u*,v**)的任意正解非退化且漸近穩定.故只需證明接近(u*,v**)的正解(u,v)唯一.取δ′>δ 充分小,這里δ 在引理7 中給出.設
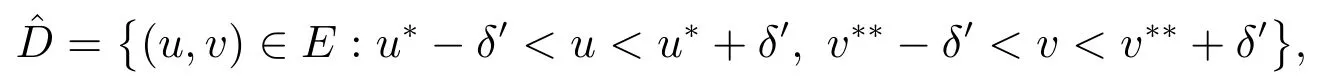
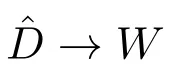
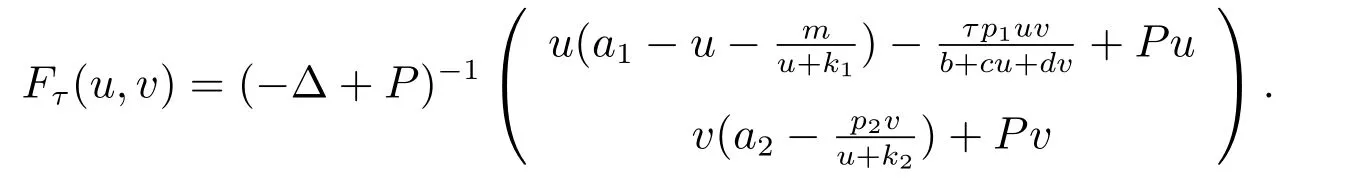

由此證明了系統(1)接近(u*,v**)的正解(u,v)唯一.
接下來證明(1)存在唯一且不穩定的類型(b)的正解.首先證明唯一性.

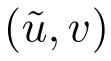
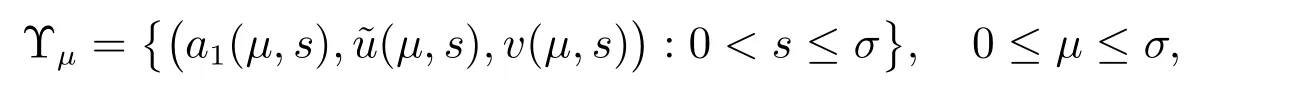
其中
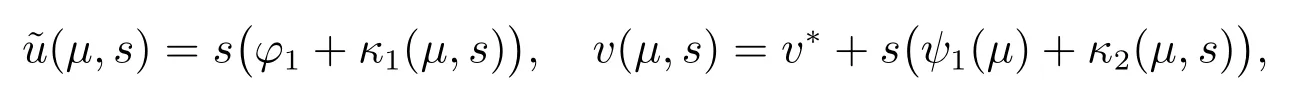
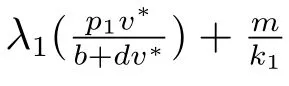
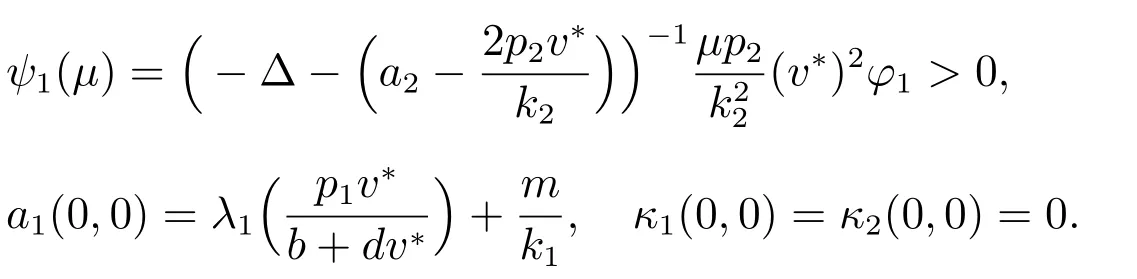
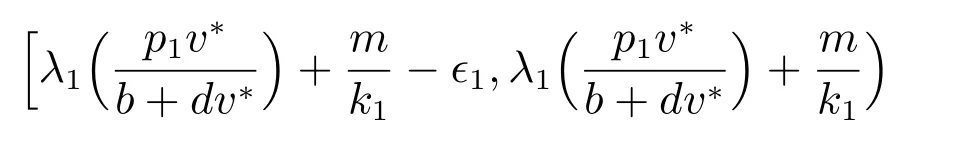
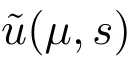
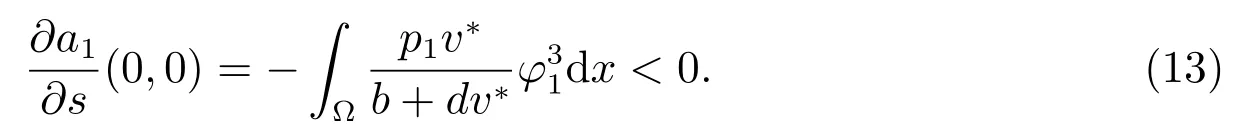
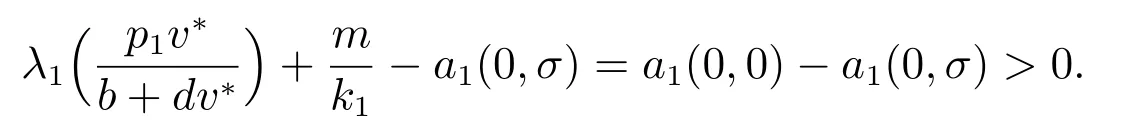
因為a1(μ,s)連續,所以存在σ1∈(0,σ],使得
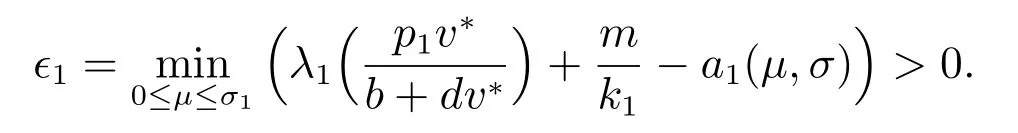
于是若
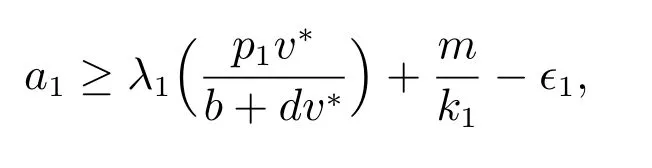
則對于任意μ ∈[0,σ1], a1(μ,σ) ≤a1.這樣我們得到對于任意的μ ∈[0,σ1], Υμ一致覆蓋a1-區域
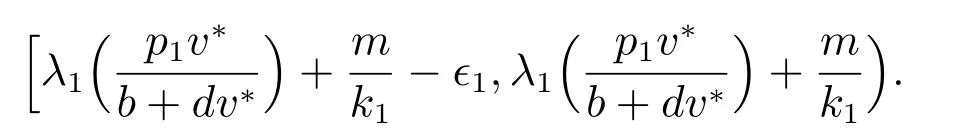
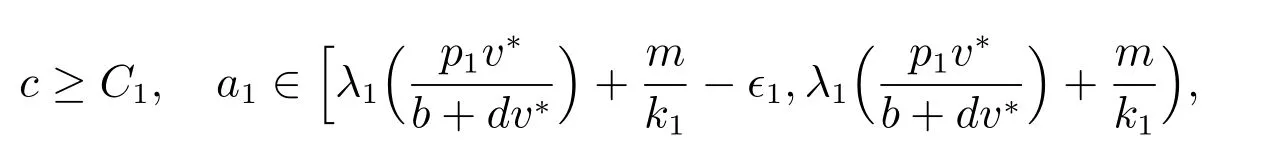
則(1)恰好有唯一(b)類型的正解.
最后,我們證明(b)類型的正解不穩定.令L1是(1)在(u,v)處帶有特征值η1和特征函數(ξ1,ζ1)的線性化算子.令L2是(12)在(cu,v)處帶有特征值η2和特征函數(ξ2,ζ2)的線性化算子.易證ξ1=ξ2, ζ1=cζ2, η1=η2.于是證明(12)于(cu,v)處的線性化算子在分歧曲線Υμ的任意點處有負的特征值γ 即可.通過文獻[14]可得存在ν >0 和C1函數
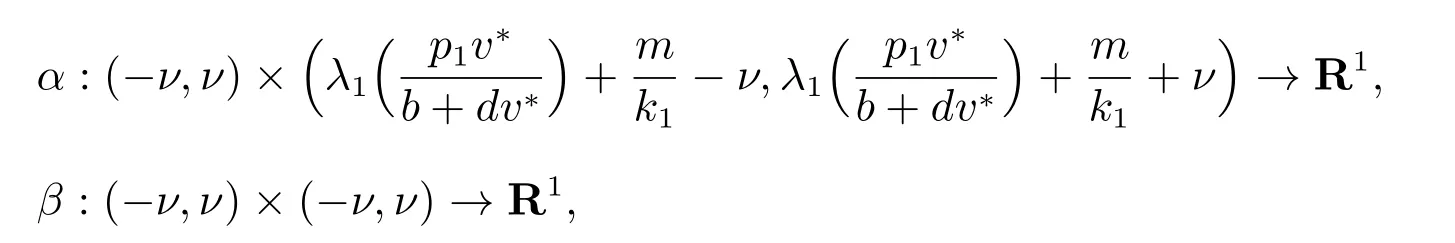
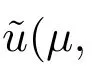
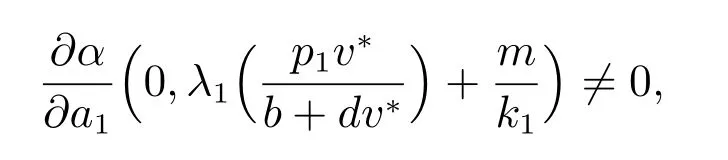
則
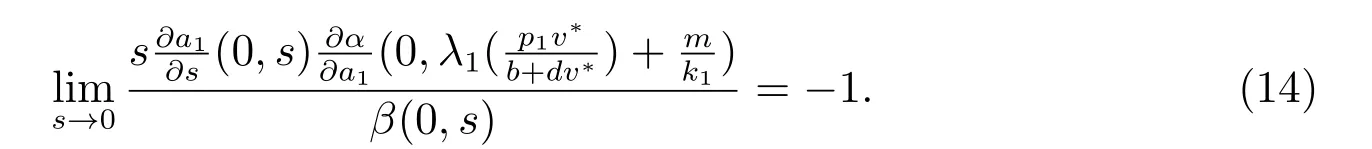
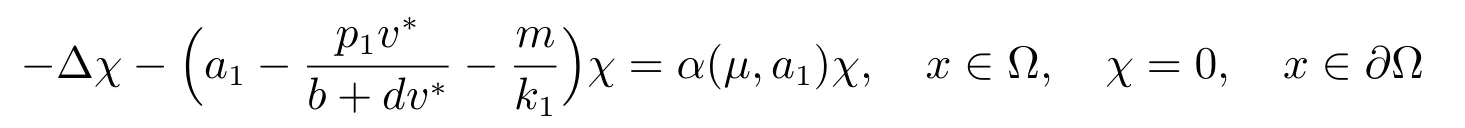
基于上面引理,這節最后給出c 充分大時確定(1)正解確切個數的重要結果.
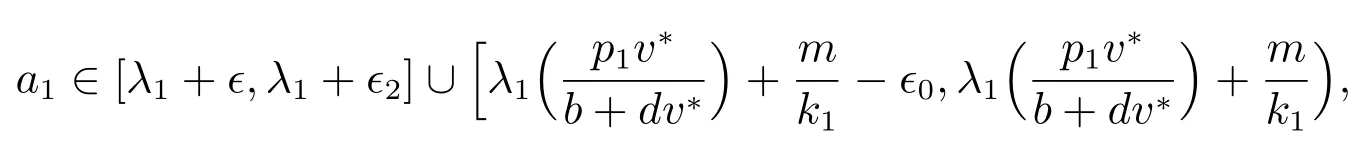
則系統(1)恰好有兩個正解,一個漸近穩定另一個不穩定.其中

證明 令
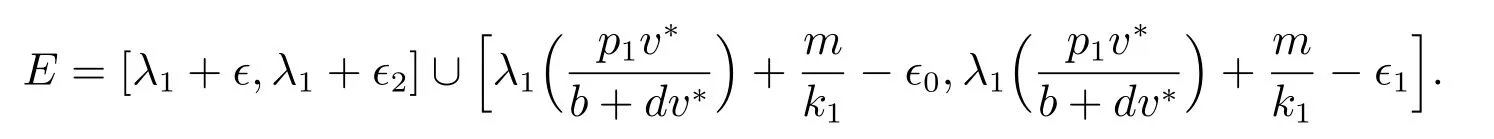
引理8 可知只需證明當a1∈E 時,(1)恰好有一個漸近穩定的正解和另一個不穩定的正解即可.引理7 表明如果c 充分大且
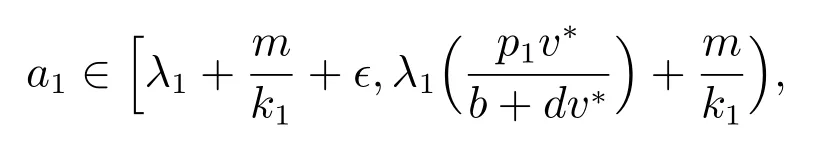
則(1)存在兩類形式的正解.采用類似引理8 的證明過程易證得,若a1∈E,則(1)存在唯一接近(u*,v**)類型(a)的漸近穩定的正解.
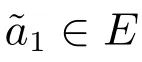
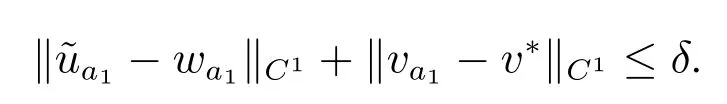
接下來,證明(1)具有類型(b)的正解不穩定.定義算子B 和B0分別如下
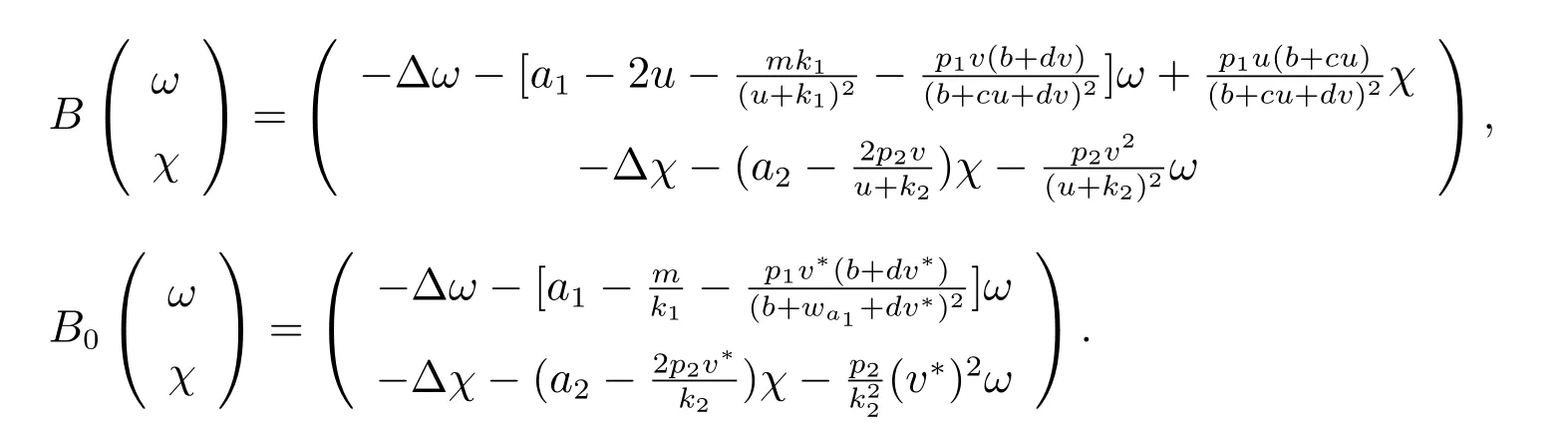
考慮如下特征值問題
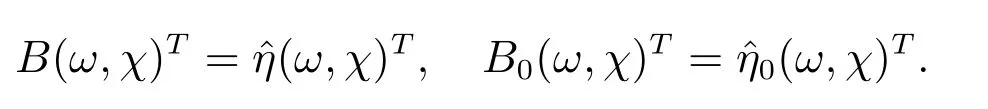
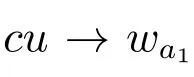
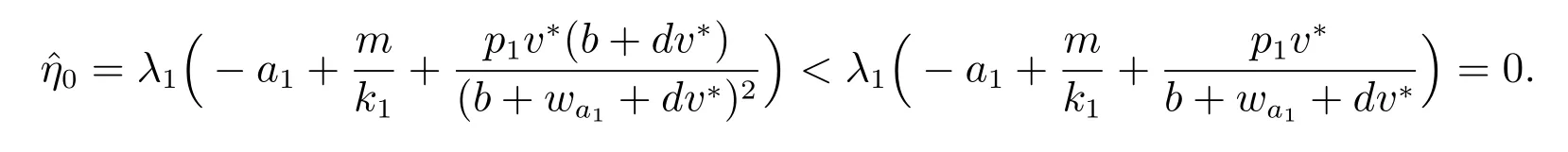
4 討論與結論
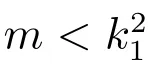
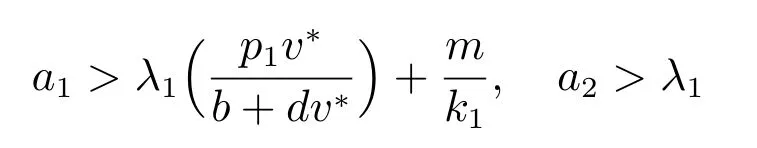
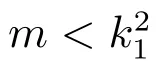
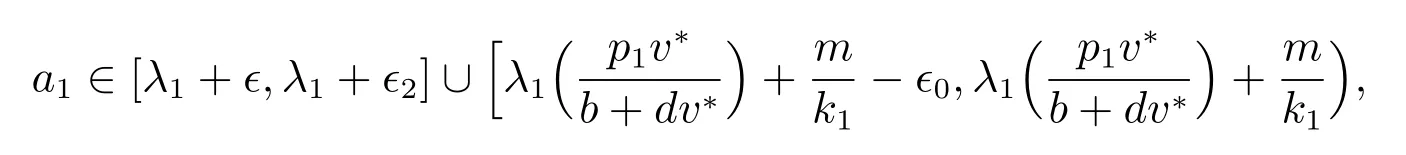
且捕食者對食餌的處理時間c 的影響充分大時食餌和捕食者不但能夠共存,而且系統恰好存在兩個正解.從生物意義上來講,研究結果表明當參數滿足一定條件時系統出現了生物上所謂的多態性,而且食餌和捕食者將會以穩定均衡的形式共存.這說明保持適合種群自身生長繁殖的最佳密度、控制種群適當的增長率以及合理地開發和利用生物資源對生物種群保護和維持生態平衡具有非常重要的意義.Allee 效應增加了系統動力學行為的復雜性,本文得到的主要結論既補充和完善了以往相關文獻的結果,又豐富了齊次Dirichlet 邊界條件下具有Allee 效應的生物擴散模型的研究內容.

