基于拓撲網絡模型的高速列車轉向架系統中薄弱部件辨識方法

何志超，王艷輝，安 超，林 帥

(1.北京交通大學軌道交通控制與安全國家重點實驗室，北京 100044;2.北京交通大學交通運輸學院，北京 100044;3.城市軌道交通運營安全管理技術及裝備交通運輸行業研發中心，北京 100044;4.中車唐山機車車輛有限公司，河北 唐山 063035)

高速鐵路以其快捷、安全、高效等優勢，已成為最主要的交通運輸方式。但是，高速列車在運營過程中一旦發生故障，可能會導致巨大的經濟損失和人員傷亡。因此，對其薄弱部件進行辨識是保障列車運營安全的必要手段。

關鍵部件在高速列車動力系統中扮演著重要角色，同時在薄弱部件辨識過程中必不可少。van der Borst等分析了核電站現有部件的重要性測度，主要包括關鍵度、風險影響值等；Wu等從風力發電機組的功能屬性的角度出發，提出了改進的Birnbaum指標。然而采用網絡理論的中心性測度等指標分析網絡中的重要性時更適用于復雜的高速列車動力系統。Wei等研究了復雜網絡理論中無標度網絡的網絡模型中各中心性測度在關鍵節點辨識中的特點；Li等在分析歷史數據的基礎上確定了地鐵系統中存在的危險及其相互關系，并利用復雜網絡理論構建了地鐵運營危險網絡，找出了在地鐵運營過程中的薄弱部件；Yang等從全局網絡結構的角度出發，基于最短路徑長度、最短路徑數和非最短路徑數構建了綜合影響矩陣以反映各節點之間的作用，為復雜網絡中的薄弱部件辨識提供了一種新的方法；Wang等以飛機為節點，以飛機防撞系統通信關系為邊緣，構建了飛機狀態網絡，并提出了一種基于復雜網絡理論的節點刪除法，能夠有效地識別出飛機狀態網絡中的關鍵沖突點；Li等在最小連接支配集(MCDS)的基礎上，提出了航空網絡中關鍵節點的識別方法，其識別結果與實際情況吻合良好。

上述研究雖然從拓撲學的角度分析了部件在系統中的重要性，但并未充分考慮到部件間的耦合作用。以往研究大多是根據專家經驗進行建模，雖然該方法較為成熟，但是存在著主觀性強的缺點。此外，部分研究是基于部件的性能是獨立的假設，這忽視了部件與部件之間的作用關系。然而在現實中，部件的故障往往是會根據連接關系(物理連接、電氣連接、信息連接)進行傳播的，從而使得上述研究結果缺乏客觀性，難以將其進行廣泛應用。目前雖然已有一些研究是在考慮系統拓撲結構的基礎上來評價系統、部件的性能，但這些研究均是基于部件處于正常狀態這一前提條件，因而研究方法僅局限于關鍵節點的辨識，辨識出的薄弱節點往往會存在一定的偏差。綜上所述，高速列車動力系統作為融合了機械、電氣、信息三種連接系統所組成的復雜系統，目前的薄弱部件辨識方法對部件間的耦合作用以及對系統影響的考慮仍有不足。因此，本文基于復雜網絡理論，構建了高速列車動力系統拓撲網絡模型，并在此基礎上利用模糊積分提出了一種改進的高速列車動力系統中薄弱部件辨識方法，最后以CRH2A型動車組轉向架系統為例進行了實例分析與驗證。

1 高速列車動力系統拓撲網絡模型構建

高速列車動力系統是由諸多機械、電氣、信息裝置構成的一類典型的復雜機電系統，其實質是通過各種連接方式實現高速列車內部的能量、信息流通，將各個獨立的設備聚合成一個高度關聯的復雜網絡，如圖1所示。從網絡的角度可將高速列車動力系統中的部件視為網絡的節點，根據系統內部的關聯屬性將機械、電氣、信息連接作為節點間的邊，依次構建高速列車動力系統機械、電氣、信息連接拓撲網絡模型分別為

G

={

V

,

E

}、

G

={

V

,

E

}、

G

={

V

,

E

}，最終融合成高速列車動力系統全局拓撲網絡模型為

G

={

V

,

E

}，具體可參考文獻[11]。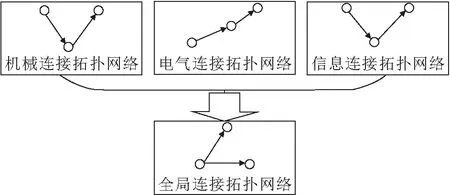

圖1 高速列車動力系統拓撲網絡構建示意圖Fig.1 Schematic diagram of high-speed train dynamical system topological network construction

通過對高速列車動力系統結構和故障數據的分析發現，系統中部件間只要存在連接，就存在失效影響關系。

2 高速列車動力系統可靠性測度指標

在高速列車拓撲網絡中節點拓撲度是指網絡中與目標節點相連的節點數，代表其對網絡相連節點的影響程度。但是，如果該節點與較多節點相連，其失效所產生的影響越大，系統可靠性越難以得到保障。然而在高速列車實際運行過程中，節點的失效還與其失效概率相關。因此，本文將綜合考慮節點拓撲度和失效概率，給出節點失效度的定義。

定義1 節點失效度為網絡中節點拓撲度與失效概率的乘積，即：

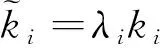
(1)

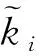
傳統復雜網絡定義中，最短路徑是指網絡中任意兩個節點間所有路徑中最短的路徑。這只是基于網絡的拓撲結構提出的，缺乏對部件自身性質的考慮。因此，本文將節點失效概率納入最短路徑的定義中，即最短失效路徑。

定義2 最短失效路徑是指節點

i

到節點

j

之間的最短失效路徑，為在考慮節點的失效影響后節點

i

發生失效后導致節點

j

失效的最有可能的路徑，其表達式為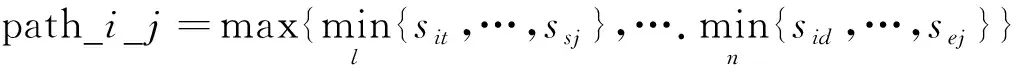

(2)

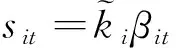
(3)

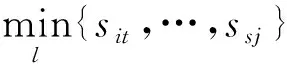
定義3 網絡的平均最短失效路徑長度為

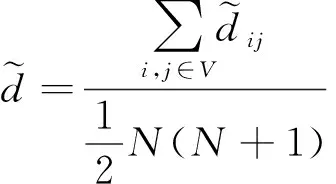
(4)

定義4 節點失效介數是指通過節點

v

的最短失效路徑的數量與網絡中所有最短失效路徑數量的比值，其表達式為

(5)

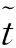
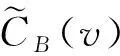
3 高速列車動力系統中薄弱部件的辨識方法

3. 1 辨識流程

在構建的高速列車動力系統中拓撲網絡模型的基礎上，利用關聯的層次多屬性決策理論，對高速列車動力系統中的薄弱部件進行辨識，具體流程如圖2所示。

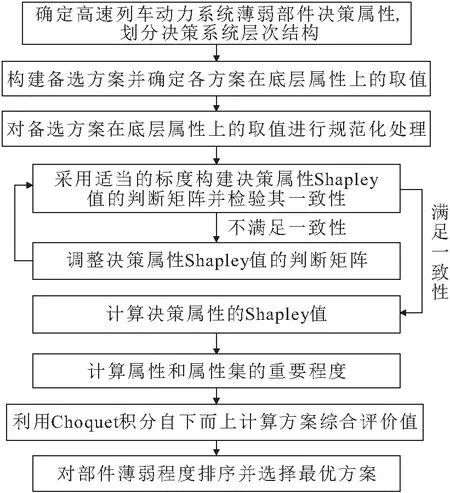
圖2 高速列車動力系統中薄弱部件的辨識流程圖Fig.2 Flow chart for identification of high-speed train dynamical system weak components

3. 2 屬性集構建

高速列車動力系統中薄弱部件不僅與節點的結構位置屬性有關，同時還與節點自身可靠性屬性相關。因此，高速列車動力系統中薄弱部件的判斷屬于多屬性決策問題。假設基于關聯的多屬性決策問題的屬性集為結構屬性

X

=(

x

,

x

)；

P

(

X

)為

X

的冪集。定義5設給定

λ

∈(-1,∞)，

g

：

P

(

X

)→[0,1]滿足條件(1)

g

(

X

)=1；(2) ?

M

,

N

∈

P

(

X

)且

M

∩

N

=

φ

，則

g

(

M

∪

N

)=

g

(

M

)+

g

(

N

)+

λg

(

M

)

g

(

N

)；(3)

g

連續。則稱

g

為定義在

P

(

X

)上的

λ

模糊測度。對?

S

∈

P

(

X

)，

g

為屬性集

S

的權重。當

λ

=0時，說明屬性間相互獨立；當-1<

λ

<0時，說明屬性間存在冗余關聯作用；當

λ

>0時，說明屬性間存在互補關聯作用。為了計算各屬性指標

x

的

λ

模糊測度，引入Shapley值便于計算。定義6若

g

為定義在

P

(

X

)上的

λ

模糊測度，對

x

∈

X

，其Shapley值

I

定義為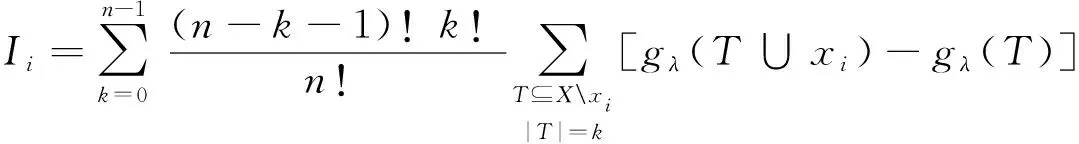

(6)

本文采用Choquet積分作為多屬性決策問題的集結算子，定義如下。

定義7若

g

為定義在

P

(

X

)上的

λ

模糊測度，離散Choquet積分定義用

f

定義為：

X

→

IR

關于

g

的映射：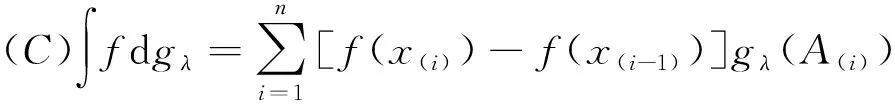

(7)

式中：(

i

)表示

f

(

x

())向量的變換，使得0≤

f

(

x

)≤…≤

f

(

x

()) ；

A

()=(

x

(),…,

x

()) ，并且

f

(

x

)=0。

3. 3 多屬性集決策模型構建

利用模糊測度和積分的層次多屬性決策來實現高速列車動力系統中薄弱部件的辨識，圖3給出了基于Choquet積分的三層多屬性決策模型。

在子屬性Choquet積分的基礎上，可求得層次

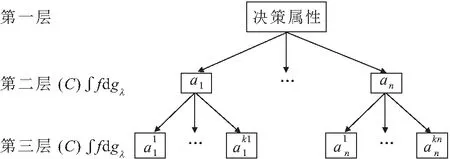
圖3 節點的決策屬性結構層Fig.3 Decision attribute structure layer of nodes

當沒有足夠決策屬性和方案偏好信息時，應用模糊測度Marichal熵的定義，以Marichal熵最大為目標函數構建優化模型，可由下式求解屬性和屬性集的重要程度：

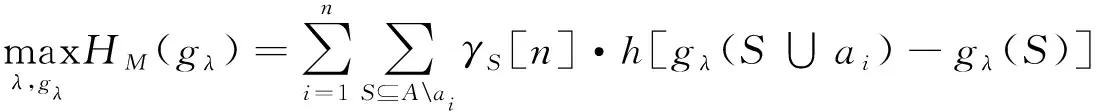
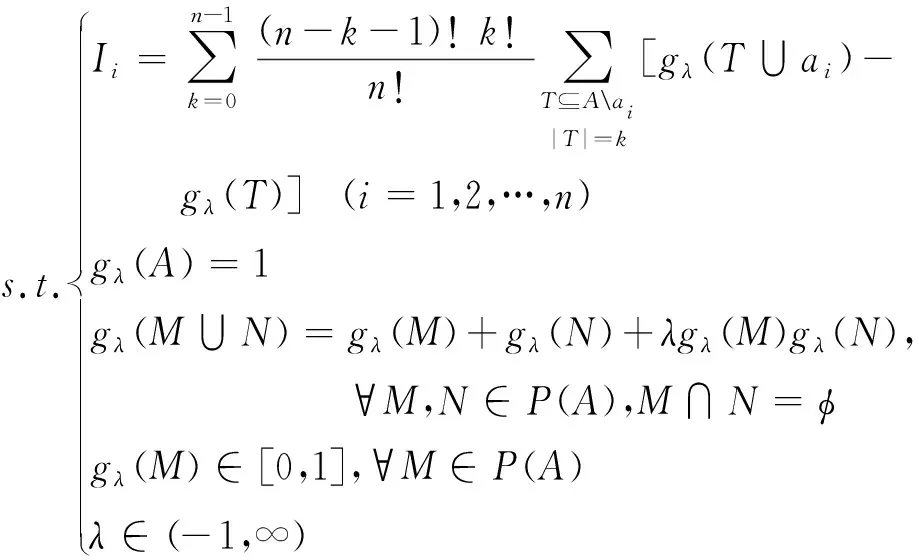
(8)

4 實例分析與驗證

本文以文獻[20]中的CRH2A型動車組的轉向架系統(部件以及部件間的連接關系是根據中車唐山機車車輛有限公司以及中車青島四方機車車輛股份有限公司調研所得)為例，對高速列車轉向架系統中的薄弱部件進行辨識。

4. 1 高速列車轉向架系統拓撲網絡模型構建

利用上述建立的高速列車動力系統中薄弱部件的辨識方法，構建高速列車轉向架系統的機械連接拓撲網絡模型、電氣連接拓撲網絡模型、信息連接拓撲網絡模型和高速列車轉向架系統拓撲網絡模型，見圖4至圖7。

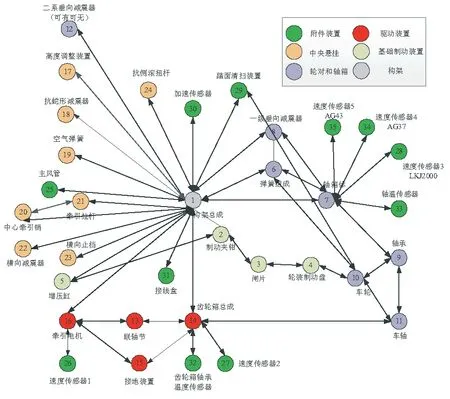
圖4 高速列車轉向架系統機械連接拓撲網絡模型Fig.4 Topological network model of mechanical connection for bogie system of high speed trains

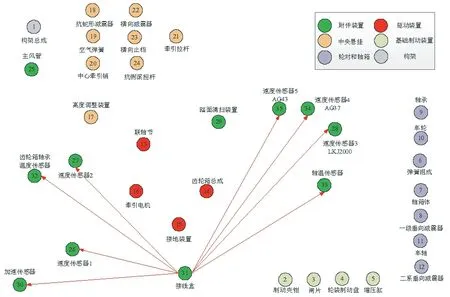
圖5 高速列車轉向架系統電氣連接拓撲網絡模型Fig.5 Topological network model of electrical connection for bogie system of high-speed trains

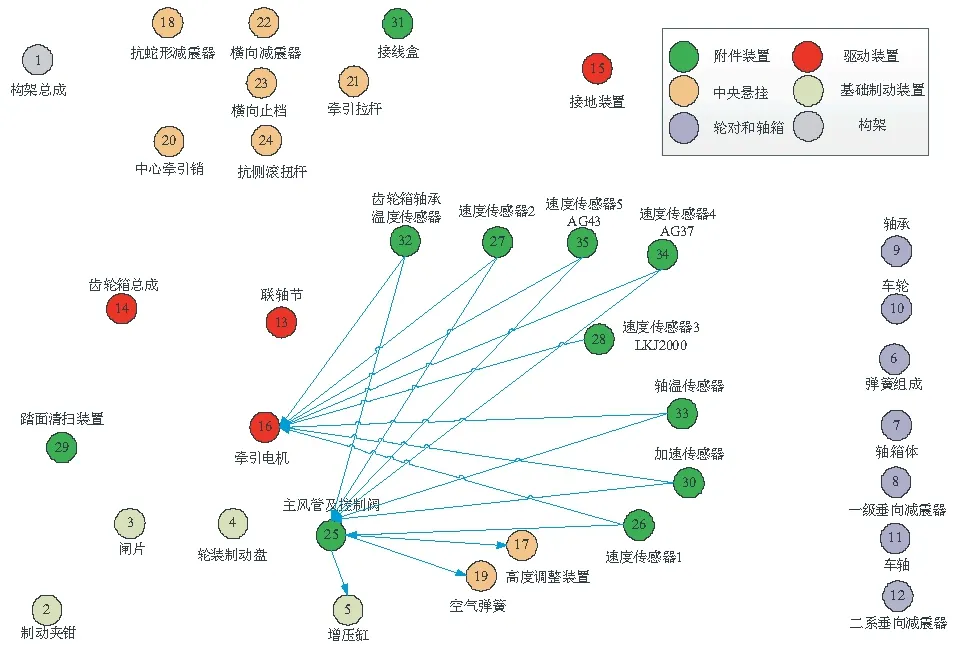
圖6 高速列車轉向架系統信息連接拓撲網絡模型Fig.6 Topological network model of information connection for bogie system of high-speed trains

圖7 高速列車轉向架系統拓撲網絡模型Fig.7 Topological network model of high-speed train bogie system

高速列車轉向架系統拓撲網絡模型是基于復雜網絡理論構建的，根據構建的高速列車轉向架系統拓撲網絡模型，對高速列車動力系統的拓撲統計特性進行分析。

4.1.1 度和度分布

一個節點的度越大，此節點所連接的其他部件就越多，因此它所代表的部件的重要程度就越大，其對系統的正常運行的影響就越大。高速列車轉向架系統及其機械、電氣、信息連接拓撲網絡模型中節點的出度和入度，見圖8和圖9。

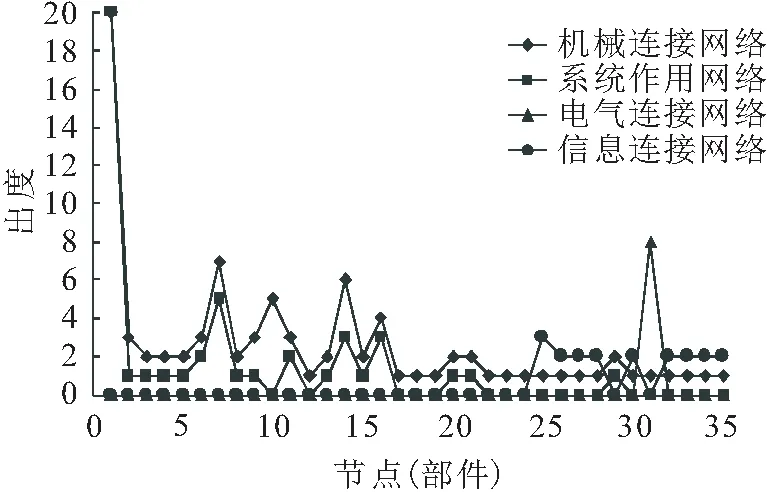
圖8 轉向架系統及其機械、電氣、信息連接拓撲網絡 模型中節點的出度分布Fig.8 Out-degree distribution of nodes in topological network models of bogie system and the mech- anical,electrical,and information connection

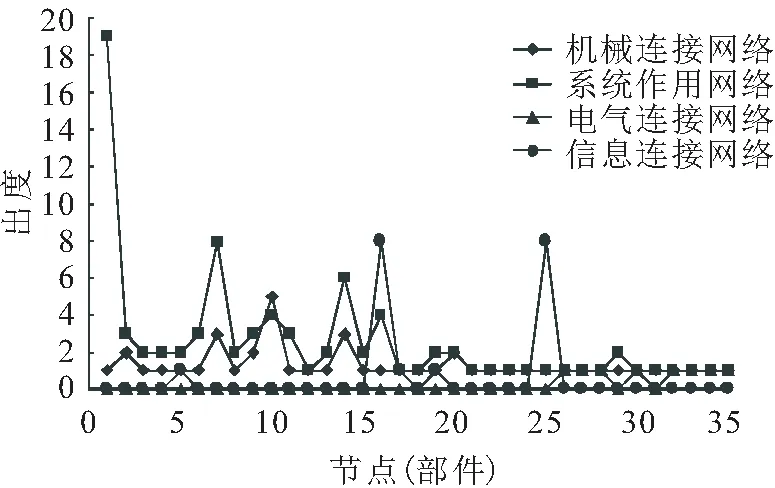
圖9 轉向架系統及其機械、電氣、信息連接拓撲網絡 模型中節點的入度分布Fig.9 In-degree distribution of nodes in topological network models of bogie system and the mech- anical,electrical,and information connection

由圖8可見，高速列車轉向架系統拓撲網絡中出度最大的部件是構架總成(節點1)，其出度為20，如果構架總成發生故障將有20個與之相關的部件被干擾。因此，構架總成是高速列車轉向架系統運行維護中需要重點關注的部件。

由圖9可見，高速列車轉向架系統拓撲網絡中入度最大的部件仍是構架總成，入度為19，有19個部件發生故障能夠影響它。其中，機械連接網絡入度最大的部件是車輪，入度為5；信息連接網絡入度最大的部件是牽引電機、主風管和控制閥，入度為8；電氣連接網絡入度最大為1，有8個部件組成。

4.1.2 平均路徑長度

通過計算每個節點到其他所有節點的最短路徑，用這些最短路徑的和除以該節點能夠到達的節點數量可得到這個節點的平均路徑長度。高速列車轉向架系統及其機械、電氣、信息連接拓撲網絡模型中節點的平均最短路徑分布，見圖10。

圖10 高速列車轉向架系統及其機械、電氣、信息連接 拓撲網絡模型中節點的平均最短路徑Fig.10 Average shortest path of nodes in topological network models of high-speed train bogie system and the mechanical,electrical, and information connection

由圖10可見，高速列車轉向架系統拓撲網絡中節點的平均路徑長度為2.22，因此如果某個部件失效，只需要傳遞1～2個部件便會影響網絡中其他部件；而機械拓撲網絡中節點的平均路徑長度為2.65，電氣拓撲網絡中節點的平均路徑長度為1，信息撲拓網絡中節點的平均路徑長度為1.56，這表明高速列車轉向架系統拓撲網絡中任何一個部件發生故障，多是通過機械連接的形式進行傳播，從而影響其他部件。

4. 2 高速列車轉向架系統網絡可靠性分析

基于所構建的高速列車轉向架系統拓撲網絡模型，計算了系統中各部件的拓撲度、故障率和失效度，其計算結果見圖11。

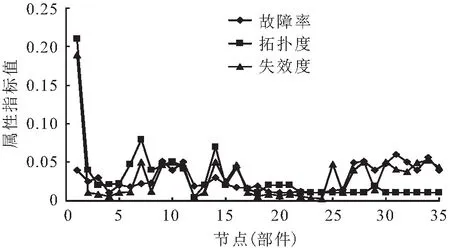
圖11 高速列車轉向架系統中各部件的故障率、拓撲度和 失效度Fig.11 Failure degree,failure rate and topological degree of high-speed train bogie system components

由圖11可見，構架總成、軸箱體、齒輪箱總成節點的拓撲度最高，構架總成、速度傳感器4 AG37、軸箱體節點的失效度較高；此外，存在少數節點拓撲度低，而失效度與之相反，如速度傳感器4 AG37節點，與其有聯系的部件相對較少，但是在實際運行過程中容易出現故障，甚至會使得列車運營停滯，因此該部件對高速列車轉向架系統十分關鍵，嚴重影響著轉向架系統的整體可靠性；構架總成在高速列車轉向架系統中有很高的拓撲度，也是該系統結構中不可或缺的部分，其失效度和拓撲度均大于其他部件。

分別計算了高速列車轉向架系統中各個部件之間的最短失效路徑和最短路徑，其結果如下：

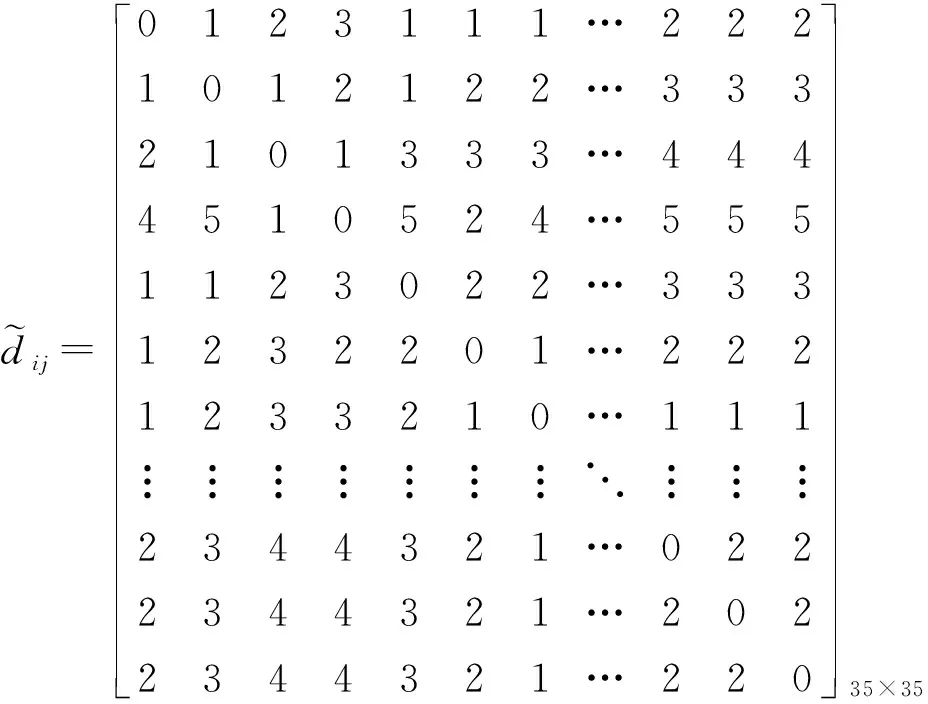
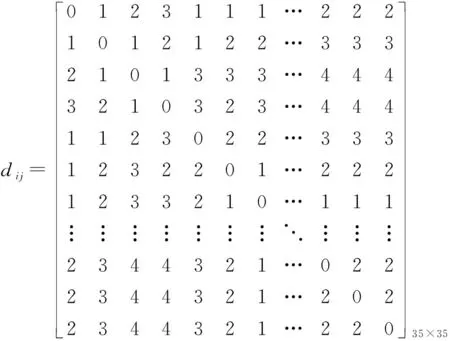
由上述計算結果不難發現，高速列車轉向架系統中各個部件之間的最短失效路徑與最短路徑的計算結果是不同的，這是因為在最短失效路徑的定義中體現了節點的失效特性，當某一節點失效時，其相關節點也可能失效，進而導致其路徑發生改變，因此其最短失效路徑與最短路徑的計算結果不一致。

高速列車轉向架系統中各部件失效介數的計算結果，見圖12。

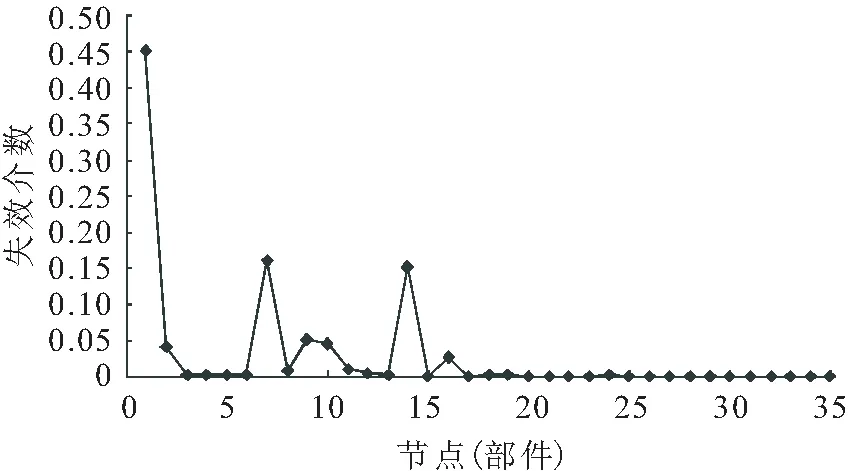
圖12 高速列車轉向架系統中各部件的失效介數Fig.12 Failure betweenness of high-speed train bogie system components

由圖12可見，構架總成、軸箱體、齒輪箱節點所對應的失效介數最大，當部件失效介數較大時，意味著其在轉向架系統中的最短失效路徑較多，因而嚴重影響了整個系統的可靠程度。

4. 3 高速列車轉向架系統中薄弱部件的辨識

本文選取高速列車轉向架系統中的35個節點為研究對象，分別用

v

,…,

v

表示，依據本文所提出的高速列車動力系統中薄弱部件的辨識方法，結合轉向架系統拓撲結構和可靠性屬性進行重要度

I

計算，其計算結果見表1。

表1 高速列車轉向架系統中薄弱部件的重要度計算結果

由表1可知，構架總成(節點1)的重要度最高，其值為3.048 8；其次為軸箱體(節點7)，其重要度為0.831 1；而二系垂向減震器(節點12)、抗蛇形減震器(節點18)、橫向減振器(節點22)、橫向止檔(節點23)和抗側滾扭桿(節點24)的重要度均大于0.4，因此，以上部件對高速列車轉向架系統的正常運行有很大的影響，且構架總成是高速列車轉向架系統中最關鍵的薄弱部件，這與實際運營情況相符；除此之外，剩余部件的重要度大多在0.2～0.4之間，取值分布均勻平緩，這些部件如果發生故障對轉向架系統的影響相對較小。因此，在高速列車轉向架系統的監測與檢測工作中，需要根據部件重要度計算結果進行分級監測，重點對構架總成進行監測，同時也要加強對軸箱體、二系垂向減震器、抗蛇形減震器、橫向減振器、橫向止檔和抗側滾扭桿等部件的檢修工作，而對于重要度相對較低的部件，則應該合理安排檢修頻率，降低相應的維護成本，有效提升高速列車運行的可靠程度。

5 結 論

(1) 本文利用復雜網絡理論，分析了高速列車動力系統的復雜特性，從機械、電氣、信息3種連接方式建立了相應的拓撲網絡模型，能夠精確地描述系統中部件間的耦合作用關系，為實現高速列車動力系統中薄弱部件的辨識奠定了基礎。

(2) 綜合考慮節點拓撲度和失效概率，構建了高速列車動力系統可靠性測度指標，提出了基于關聯的層次多屬性決策的高速列車動力系統中薄弱部件辨識方法。方法的邏輯性較好，可計算性較強，只需掌握決策屬性Shapley值判斷矩陣信息即可，可有效緩解決策者的壓力。

(3) 通過對CRH2A型動車組轉向架系統的實例應用研究，結果發現構架總成、軸箱體、二系垂向減震器、抗蛇形減震器、橫向減振器、橫向止檔和抗側滾扭桿構架總成是高速列車轉向架系統中的主要薄弱部件，加強對這些部件的監測與檢修工作，對于轉向架系統的維護具有重要意義。