連續排水邊界下雙層地基一維非線性固結解析解

楊曉燕，宗夢繁，吳文兵，2，3，梅國雄，2，3，蔣國盛?

（1.中國地質大學工程學院，湖北武漢 430074；2.廣西大學土木建筑工程學院，廣西南寧 530004；3.廣西大學工程防災與結構安全教育部重點實驗室，廣西南寧 530004）

由于地基的成層性和非線性，雙層地基的一維非線性固結研究具有重要的理論和工程意義.Davis和Raymond[1]基于e-lgσ′關系，假定固結過程中滲透系數kv與壓縮系數mv同步變化且自重應力沿深度保持不變，得到kv和mv隨深度及時間變化的土體一維非線性固結理論.由于一維非線性固結求解的復雜性，現有的土體一維非線性固結解析解相對較少，其中成層地基一維非線性固結解析解仍然很少，Xie等[2-4]基于Davis和Raymond的假定，推導出雙層地基瞬時加載及單級加載、單層地基單級加載及循環加載條件下一維非線性固結問題的解析解.施建勇等[5]基于雙曲線壓縮模型建立了土體一維非線性固結方程并獲得了解析解.Lekha等[6]基于e-lgσ′和elg kv關系，在作出進一步簡化假定后推導出瞬時荷載下土體一維非線性固結解析解.而對于其他更復雜的情況，往往只有半解析解[7-10]和數值解[11-15].但以上非線性固結理論的研究僅限于對土體非線性壓縮和滲透特性的不斷深入，而對土體排水邊界隨時間發展過程的研究還不夠深入.

目前，土體固結問題的研究主要集中在固結方程和初始條件的優化上，有關邊界條件的研究相對較少.Terzaghi邊界已廣泛用于求解固結問題，其形式簡單但邊界只能表示為完全透水和完全不透水兩種.雖然有一些關于半透水邊界的報道，如Gray[16]最早對半透水邊界進行了研究，隨后Schiffman和Stein[17]、方開澤[18]也對半透水邊界進行了研究，但半透水邊界求解相對困難.基于此，梅國雄等[19]提出與時間相關的連續排水邊界并得到瞬時荷載下的單層一維固結方程的解答；隨后，蔡烽等[20]、Liu和Lei[21]、Wang等[22-23]、吳文兵等[24-27]對基于連續排水邊界的土體固結問題進行了跟蹤研究.但以上基于連續排水邊界的固結研究中均未綜合考慮地基的成層性和土體非線性特性，而地基成層性和土體非線性對固結性狀的影響不容忽視.

本文基于Davis和Raymond的假定推導出連續排水邊界條件下瞬時加載的雙層地基一維非線性固結解析解，基于所得解詳細討論了連續排水邊界界面參數及非線性參數對土體一維非線性固結特性的影響.然后與Xie等[3]所得解進行對比，驗證解答的合理性.

1 連續排水邊界

土體固結特性非常復雜，不僅與土體參數有關，排水邊界形式對土體固結特性也有很大影響.運用最廣的邊界形式是傳統Terzaghi排水邊界，包括完全排水和完全不排水兩種形式，表達式分別為式（1）和式（2）.

式中：u為超靜孔隙水壓力；z為土層深度豎直向下的坐標.

由于Terzaghi排水邊界只能反映出邊界完全排水和完全不排水兩種較為絕對的排水狀態，在實際工程中邊界排水能力可能介于這兩者之間，因此Gray[16]提出半透水邊界，其表達式如下：

半透水邊界能夠反映邊界處孔壓隨時間消散情況，但由于形式較為復雜，致使固結方程求解困難，難以求得解析解答.梅國雄等[19]認為Terzaghi排水邊界與初始條件存在數學不適定問題，且實際排水邊界介于完全排水和不排水之間，因此提出與時間相關的連續排水邊界，其表達式如下：

式中：q0為施加的瞬時外荷載；t為時間；b為連續排水邊界的界面參數.

對連續排水邊界無量綱化處理，令：

式中：cv為固結系數；α 為無量綱的界面參數，其值可以通過試驗模擬或工程實測反演得出.

此時，連續排水邊界可改寫為：

2 雙層地基一維非線性固結模型

雙層地基一維非線性固結分析模型如圖1所示.圖中hi為土層i（i=1，2）的厚度，地基總厚H=h1+h2；q0表示作用于土體的瞬時荷載.由Davis和Raymond[1]的假定可得出土體一維非線性固結方程如下：

圖1 雙層地基模型Fig.1 Schematic diagram of double-layered soil

定解條件為：

由有效應力原理知：

3 連續排水邊界條件下雙層地基一維非線性固結解答

固結方程式（7）為非線性偏微分方程，為將方程變為線性偏微分方程，令：

將式（12）代入固結方程式（7），則固結方程可化簡為：

為了進一步將邊界條件齊次化，令：

將式（14）代入化簡后的固結方程式（13），則固結方程進一步表達為：

其中：

相應的定解條件變為：

設方程式（15）解的形式如下：

其中：

式中：βm、μ、λm、Am、Bm和Cm為待定系數；Tm（t）為關于t的待定函數.當待定系數和待定函數確定后，方程式（15）的解答就可以確定.將式（22）和式（23）代入式（21）后，顯然滿足邊界條件式（19）.

將層間連續條件式（20）代入待定函數式（21），得：

其中：

式（25）為確定待定系數λm的特征方程.將式（21）代入邊界齊次化后的固結方程式（15），可得：

由正交關系可得：

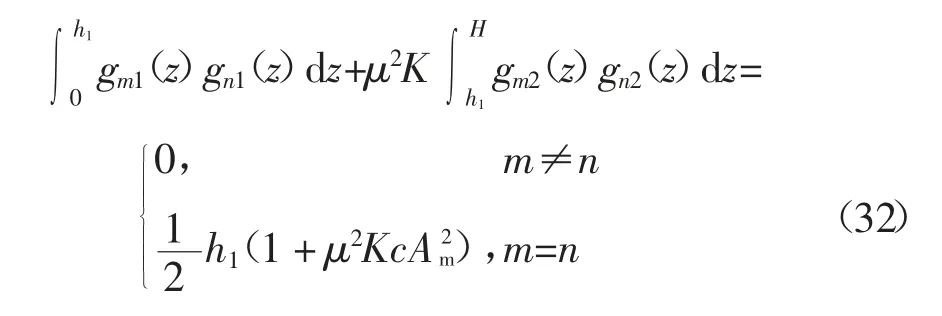
結合式（29）和式（32），可以確定系數Cm為：

將初始條件式（18）代入待定方程式（21）可得：

考慮方程式（34）的恒等性，可以確定系數Bm為：

方程式（21）的待定系數及待定函數都已確定，因此求出一般解為：

將式（36）和式（37）代入式（14），可得ω1和ω2：

式中：待定系數c、βm、μ、Am、Cm分別由式（26）（27）（28）（24）（33）確定；待定系數Tm由式（25）確定；λm由式（25）確定.由式（14）可以得到第一層土和第二層土超靜孔隙水壓力的表達式如下：

雙層地基按沉降定義的地基總平均固結度Us和按有效應力定義的地基總平均固結度Up分別為：

式中：εi和εfi分別為土層i的豎向應變和最終豎向應變，且有：

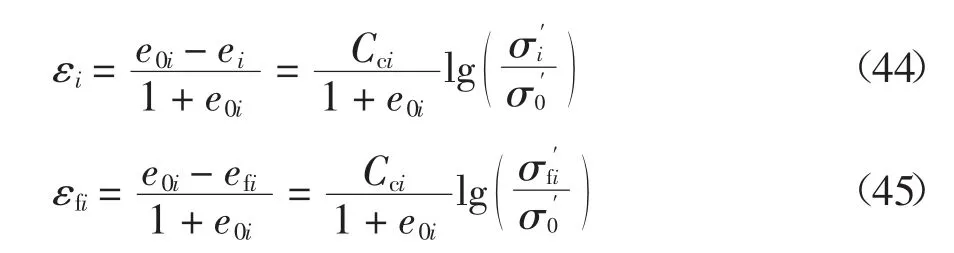
4 解答的驗證與分析

基于Davis和Raymond的假定，Xie等[3]得到了Terzaghi雙面排水及單面排水雙層地基一維非線性固結解答.本節通過與Xie的理論解進行全面對比，對本文解的合理性進行分析.

圖2反映了土層壓縮系數比值對按沉降定義的平均固結度Us的影響.圖中Tv為時間因數，表達式前文已給出.由圖2可以看出界面參數r取值等于1 000時，基于連續排水邊界固結解答與Xie雙面排水解答一致，表明界面參數取值較大時，連續排水邊界將退化為Terzaghi完全排水邊界，初步驗證了解答的正確性.此外，從圖中還可以看出隨著下層土與上層土壓縮系數比值的減小，雙層地基固結速率變快，表明上軟下硬型地基固結更快.

圖2 壓縮系數對Us曲線的影響Fig.2 Influence of compressibility coefficient on Uscurves

圖3反映了連續排水邊界條件下最終有效應力與初始有效應力比值Nσ對Us和Up的影響.由于kvi、mvi值隨Nσ值的增大而同步減小[7-8]，固結過程中kvi減小則土體內孔隙水越難排出即孔壓越難消散，而mv值減小則土體越難被壓縮即孔壓越容易消散，因此kvi減小則固結速率減小，而mvi值減小則固結速率增大.從圖3中可以看出固結度曲線隨Nσ取值不同而發生改變，說明kvi、mvi對固結度的影響并未抵消.圖中Us隨Nσ值的增大而增大，而Up隨Nσ值的增大而減小，這說明連續排水邊界條件下，按沉降定義的平均固結度計算時，壓縮系數對固結速率起主要作用；而按孔壓定義的平均固結度計算時，滲透系數對固結速率起主要作用.此外，從圖3可以看出對于同一時間因數Tv，Us值均大于Up值，且兩者的差別隨著Nσ值的增大而增大，說明雙層地基一維非線性固結的沉降速率大于孔壓消散速率.

圖3 Nσ值對固結度的影響Fig.3 Influence of Nσon consolidation degree of soil

圖4和圖5分別反映了不同邊界條件下Nσ值對Us和Up的影響.由圖4可以看出對于Xie單面及雙面排水解答，Us不隨Nσ值的變化而變化，這說明kvi和mvi對Us的影響相互抵消；而基于連續排水邊界所得解答Us隨Nσ值的增大而增大.邊界的排水會影響土體變形的發展過程，排水邊界不同則土體變形過程也會產生差異，因此圖4中Xie所得解答Nσ值對Us沒有影響，而連續排水邊界下Nσ值對Us有影響，這可能是排水邊界不同引起的.由圖5可以看出連續排水邊界解答和Xie單面及雙面排水解答，Up均隨Nσ值的增大而減小，這說明按孔壓定義的平均固結度計算時，滲透系數對固結速率起主要作用.此外，從圖5還可以看出連續排水邊界條件下Nσ對Up的影響遠小于Xie所得解答下Nσ對Up的影響.

圖4 不同邊界條件下Nσ值對Us曲線的影響Fig.4 Influence of Nσon Uscurves for different boundary conditions

圖5 不同邊界條件下Nσ值對Up曲線的影響Fig.5 Influence of Nσon Upcurves for different boundary conditions

圖6反映了界面參數r值對按沉降定義的固結度的影響.從圖中可以看出土體固結速率隨r值的增大而增大.在固結初期，連續排水邊界條件下土體固結速率小于Xie解答下的土體固結速率，但在固結中后期，連續排水條件下固結速率在Xie單面和雙面排水條件之間變化，值越大越接近于雙面排水，越小越接近于單面排水.當r取值較大時，連續排水邊界條件得到的固結曲線與Xie雙面排水得到的固結曲線相近；而當r取值較小時，連續排水邊界條件得到的固結曲線與Xie單面排水得到的固結曲線幾乎一致，這表明Xie解答的固結初期較快，而基于連續排水邊界所得解答后期固結更快.對于實際工程而言，當排水邊界參考連續排水邊界模型進行設計時，可以通過調整r取值來設計實際工程中需要的固結排水速率.

圖6 r值對Us曲線的影響Fig.6 Influence of r on Uscurves

在控制其他條件不變的情況下，圖7分析了土體滲透系數對孔壓曲線的影響.從圖中可以看出，如果上土層孔壓消散慢則下土層孔壓消散速度快，反之上土層孔壓消散快則下土層孔壓消散慢，即滲透系數對孔壓的影響在上土層和下土層表現相反.kv02/kv01比值越大表明上土層滲透系數相對于下土層滲透系數變小，對于上層土，孔壓隨比值kv02/kv01的增大而增大，即kv02/kv01比值越大上層土的孔壓越難消散，說明上土層滲透系數相對于下土層滲透系數小時，上土層的孔壓越難消散；反之，kv02/kv01比值越大下層土的孔壓越容易消散，說明下土層滲透系數比上土層滲透系數大時，下土層孔壓越容易消散.這表明上下土層中滲透系數相對較大的土層其孔壓消散更快.

圖7 土體滲透系數對孔壓曲線的影響Fig.7 Influence of the permeability of the soil on excess pore water pressure distribution curve

圖8分析了土體體積壓縮系數對孔壓曲線的影響.從圖8中可以看出，瞬時荷載作用下，在上下土層滲透性大小相等的情況下，孔壓隨mv02/mv01值的減小而減小，mv02/mv01值變小表明下土層體積壓縮系數與上土層體積壓縮系數比值變小，即上層土壓縮模量與下層土壓縮模量的比值變小.孔壓隨mv02/mv01的減小而減小，表明上軟下硬型的地基超靜孔隙水壓力消散更快，該類土層固結更快.

圖8 土體體積壓縮系數對孔壓曲線的影響Fig.8 Influence of the compressibility of the soil on excess pore water pressure distribution curve

5 結論

本文基于Davis和Raymond土體一維非線性固結的假設，通過引入連續排水邊界條件推導出瞬時加載下雙層地基的一維非線性固結問題的解析解.利用所得解析解，對雙層地基非線性固結進行分析，得到以下結論：

1）連續排水邊界條件下Us隨Nσ值的增大而增大，而Up隨Nσ值的增大而減小，說明利用Us計算地基固結度時，體積壓縮系數對固結速率起決定性作用，而利用Up計算地基固結度時，滲透系數對固結速率起決定性作用.

2）連續排水邊界條件下Nσ對Up的影響遠小于Xie所得解答下Nσ對Up的影響.

3）在固結初期，連續排水邊界條件下土體固結速率小于Xie解答下的土體固結速率.但在固結中后期，連續排水條件下固結速率在Xie單面和雙面排水條件之間變化，r值越大越接近于雙面排水，r越小越接近于單面排水.

4）連續排水邊界條件下雙層地基一維非線性固結，Us大于Up，且兩者的差別隨著Nσ值的增大而增大.