一種導向矢量失配的魯棒波束形成算法

崔 琳，張熠鑫，焦亞萌

(西安工程大學 電子信息學院，陜西 西安 710048)

0 引 言

波束形成技術是陣列信號處理領域中的一個重要研究分支，被廣泛地應用于雷達、聲吶、醫學成像、無線通信等諸多領域。其工作原理是通過對空間中各個陣元所接收的數據進行加權，從而達到增強期望信號、抑制干擾信號和降低噪聲的目的[1]。但當陣列對空間中的信號響應存在誤差時，自適應波束形成器的魯棒性會嚴重下降[2]。其中，DL技術[3-6]一種有效的增強自適應波束形成魯棒性的方法。

SVM是統計學習理論中一種具有良好泛化能力、非常有效的機器學習方法[7-8]，以結構風險最小化原則而被應用于多種領域。例如，信號處理中的波束形成領域，最早是由Gaudes等提出，將SVM與波束形成中的MVDR相結合，達到有效抑制波束旁瓣的效果[9]；林關成等采用迭代重加權最小二乘算法代替二次規劃，直接將SVM與波束形成算法相結合，在干擾信號較多情況下有效解決了波束形成的魯棒性問題[10]。崔琳等將SVM的基本理論與DL方法相結合，提出的波束形成算法有效提高了波束形成器存在DOA估計失配和陣元位置擾動等非理想情況下的魯棒性[11]。

PSO算法是由KENNEDY與EBERHART教授在1995年提出的[12-15]，以搜索精度高、收斂速度快等特點而被廣泛用于解決非線性優化問題[16-18]。孫榮光等將PSO引入MVDR的求解過程，利用PSO通過尋優獲得陣列的最優權向量，提高了算法抑制干擾的能力，但在小快拍數條件下，最優權值向量精度受困于收斂判據的限制[19]。HUANG等提出用分區搜索的方法，即將陣列權矢量的相位空間分成若干子區域分別進行搜索，該算法的收斂速度快，但計算復雜度高，且只考慮了相位空間，導致波束的魯棒性不太理想[20]。

本文在對角加載采樣矩陣求逆(diagonal loading sampling matrix inversion，LSMI)波束形成算法的基礎上，以陣列輸出功率最小化為目標，使用線性ε-不敏感損失函數，建立料子群支持向量機對角加載(PSO-SVM-LSMI)魯棒波束形成的優化模型，最后對波束形成優化模型進行尋優求解。

1 SVM-LSMI波束形成算法

假設空間有K個遠場窄帶信號源，全向性陣元數為M的陣元以陣列間距為λ/2的均勻線列陣分布,其中λ為信號波長。則在某一時刻k基陣的觀測值為

(1)

式中：s(k)，i(k)，n(k)分別為期望信號、干擾信號和噪聲；Ki為干擾的個數；θs為期望信號的來波方向；θij為干擾信號的來波方向；a(θs)和a(θij)分別為期望信號和干擾信號的陣列流形矢量。則傳統的窄帶波束形成器的輸出可寫為

y(k)=wHx(k)

(2)

式中：w=[w1,w2,…,wM]T為陣列的復權矢量;x(k)=[x1(k),x2(k),…,xM(k)]T為陣列的復觀測值。

LSMI波束形成器的設計問題可以表述為

(3)

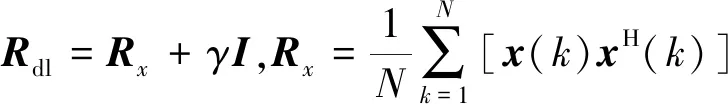
根據SVM的理論特點，需要重新構建基于標準SVM的LSMI波束形成算法的優化模型為

(4)

式中：yi為波束形成器的期望輸出；|yi-wHa(θi)|ε=max{0，|yi-wHa(θi)-ε|}為ε-不敏感損失函數。根據支持向量機的使用特點，需要在實變量條件下對該優化問題進行轉換改寫，其形式為

(5)

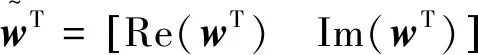
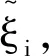
(6)

式(6)滿足的約束條件為

(7)

(8)

(9)

2 PSO-SVM-LSMI波束形成算法

2.1 PSO算法

設m為粒子群的種群數量，第i個粒子在2M維權空間的位置矢量為Zi=[z1…z2M]T，粒子在權空間的移動速度矢量為Vi=[v1…v2M]T，粒子在權空間位置的優劣由目標函數確定。記Pi為第i個粒子的歷史最優位置，Pg為整個粒子群中最優粒子的位置，對于第n次迭代，粒子更新公式為

(10)

(11)

式中：d為慣性權重因子;0≤r≤1;c1和c2為學習因子;N為最大迭代次數;Pi表示粒子的個體極值;當Pg保持不變時，迭代終結，Pg即為全局最優解。

2.2 搜索空間的確定

設由式(4)得到的最優解為

w=[w1,w2,…,wM]=Aiejφi

(12)

式中：向量A的元素表示優化權向量各元素的模;φ表示優化權向量各元素的相位，且φi=2ki，Ai≤1，i=1,2,…,M。因此，權矢量搜索空間應滿足Ai∈(0,1)和ki∈(0,1),i=1,2,…,M。

設w=[w1,w2,…,wM]為第i個粒子對應的復權矢量，則約束條件可表示為

(13)

具體的實現方法為

(14)

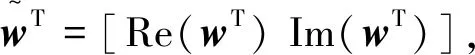
3 仿真實驗與結果分析

假設一窄帶遠場信號，全向性陣元數M為16的陣元以陣列間距為半波長的均勻線列陣分布。理想的期望信號波達方向為90°，而實際的期望信號波達方向為88°，干擾的入射方向為28°、67°、130°，干噪比均為20 dB。將陣元放在z軸上，陣元的位置在y和z方向上存在隨機的位置擾動，且擾動為統計獨立的零均值高斯隨機變量，σp表示擾動標準偏差。根據經驗以及調試,設定SVM的參數：懲罰參數C為1，誤差容限ε為0.001。設定PSO算法的參數：慣性權重因子d為0.8，學習因子c1和c2為1.5，種群規模為200，最大迭代次數N為100。

實驗1：理想情況下,即無失配時的情況。仿真選取的快拍數為512，信噪比(signal-to-noise ratio, SNR)分別為0 dB和20 dB，其中，SVM-LSMI為文獻[11]提出來的魯棒波束形成算法。則理想情況下即無失配時的波束圖如圖1所示。

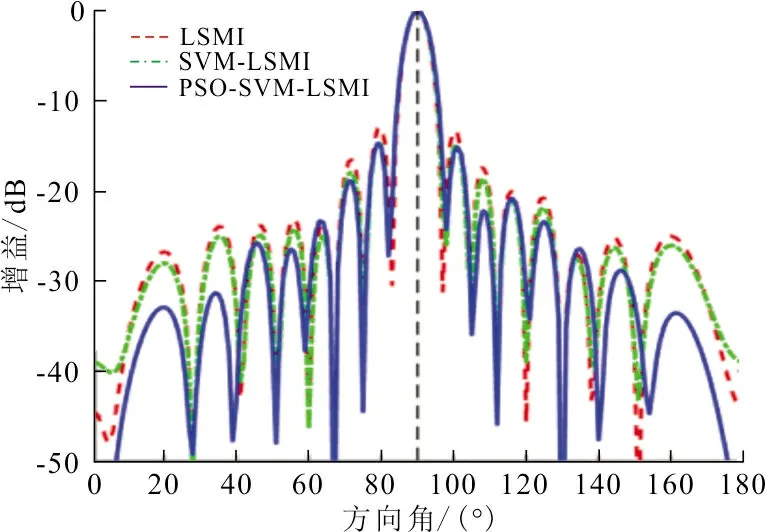
(a) 0 dB

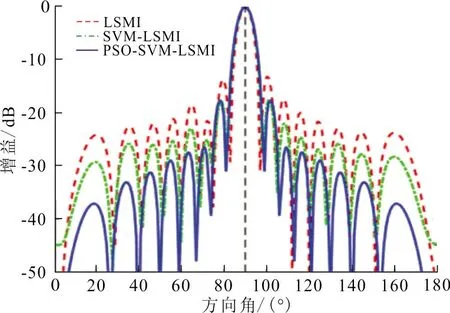
(b) 20 dB圖 1 無失配時不同SNR的波束圖Fig.1 The beam pattern at different SNR without mismatch

從圖1(a)、(b)可以看出，當SNR較低時，3種算法均在獲得較理想的波束指向的同時擁有良好的旁瓣級；當SNR較高時，LSMI和SVM-LSMI算法的旁瓣在一定程度上有所升高，但對干擾仍具有較強的抑制能力，算法的性能有所下降。而PSO-SVM-LSMI波束形成算法不僅可以獲得較理想的波束指向、主瓣寬度和有效的干擾抑制能力，尤其在SNR較高時，可以獲得比LSMI和SVM-LSMI算法更低的旁瓣級。說明在高SNR的情況下，PSO-SVM-LSMI算法在繼承原有LSMI算法特性的基礎上，同時結合PSO-SVM的優點，使該算法具很強的魯棒性。

實驗2：DOA失配2°時的情況。其他仿真條件均和實驗一相同。則DOA失配2°時的波束圖如圖2所示。

從圖2(a)、(b)可以看出，當期望信號的波達方向估計存在失配時，由于LSMI算法誤將期望信號當做干擾加以抑制，因而LSMI和SVM-LSMI算法的主瓣出現了指向性偏差。特別是當信噪比較高時，這2種算法雖然可以獲得較強的干擾抑制能力，但波束的旁瓣迅速升高，算法的性能嚴重下降。

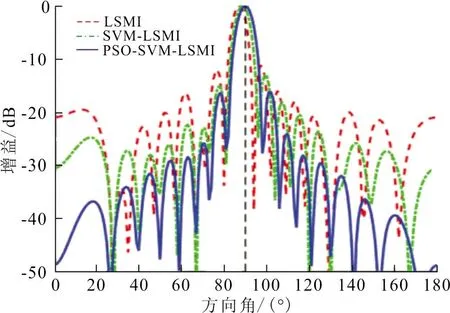
(a) 0 dB

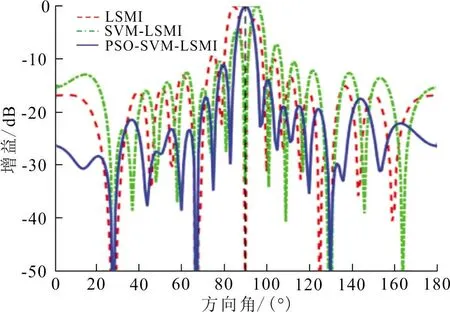
(b) 20 dB圖 2 失配2°時不同SNR的波束圖Fig.2 The beam pattern with different SNR at 2 degree of mismatch

而PSO-SVM-LSMI算法的旁瓣級雖然在SNR較高時有所升高且發生輕微畸變，但無論SNR的高低，都沒有因為期望信號的波達方向失配而對波束的指向性造成影響，而且對干擾信號也具有很強的抑制作用。說明在期望信號波達方向估計失配的情況下，PSO-SVM-LSMI算法有效的解決了對信號指向誤差敏感的影響，比LSMI和SVM-LSMI算法具有更強的魯棒性。

實驗3：陣元位置存在擾動偏差時的情況，如圖3所示。

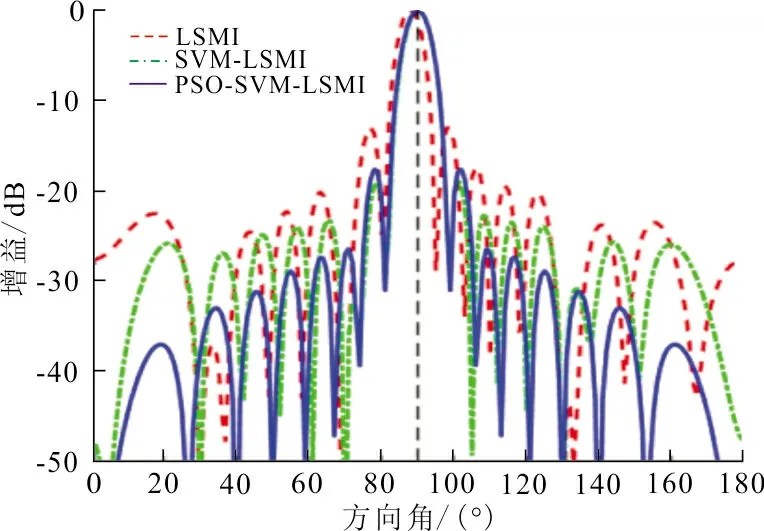
(a) 0.02λ

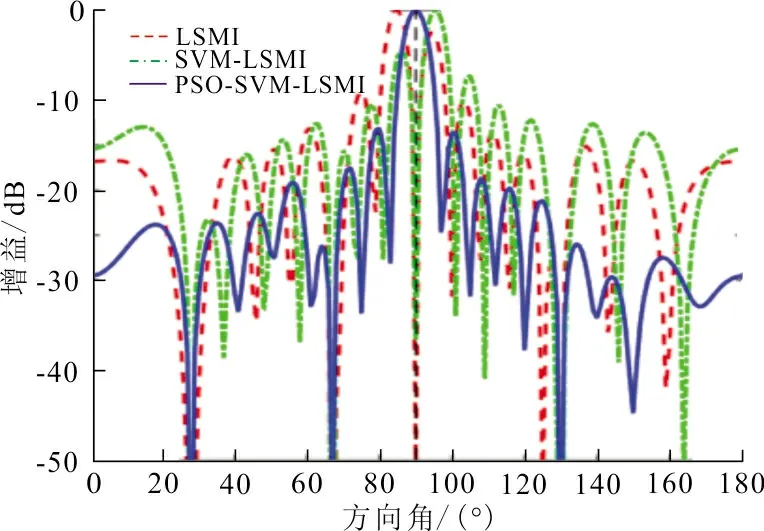
(b) 0.20λ圖 3 SNR為0 dB時不同擾動偏差的波束圖Fig.3 The beam pattern with different disturbance deviation at 0 dB of SNR

圖3(a)的擾動標準偏差為0.02λ，圖3(b)的擾動標準偏差為0.20λ，SNR為0 dB，其他仿真條件均與實驗1相同。

從圖3圖(a)、(b)可以看出，在信噪比較低的條件下，當擾動偏差為0.02λ時，LSMI算法的主瓣出現了些許的指向性偏差，且隨著擾動偏差的增大，主瓣指向性的偏差程度在加劇，同時旁瓣也迅速升高，但仍然具有良好的干擾抑制能力。SVM-LSMI算法在擾動偏差為0.02λ時，算法的性能良好，但隨著擾動偏差的增大，波束主瓣不僅出現指向性偏差，且在旁瓣迅速升高的同時伴隨畸變現象的發生。而PSO-SVM-LSMI算法雖然隨著擾動偏差的增大，波束的旁瓣出現了輕微程度地畸變，但仍然可以獲得較理想的主瓣指向和主瓣寬度，并且具有很強的干擾抑制能力，其性能基本穩定。說明在SNR較低,且存在位置擾動的情況下，PSO-SVM-LSMI算法比LSMI和SVM-LSMI算法的魯棒性強。

實驗4：將SNR設置為20 dB，其他仿真條件均與實驗3相同，則陣元位置存在擾動偏差時的波束圖如圖4所示。

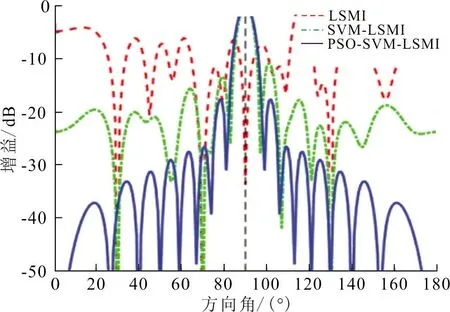
(a) 0.02λ

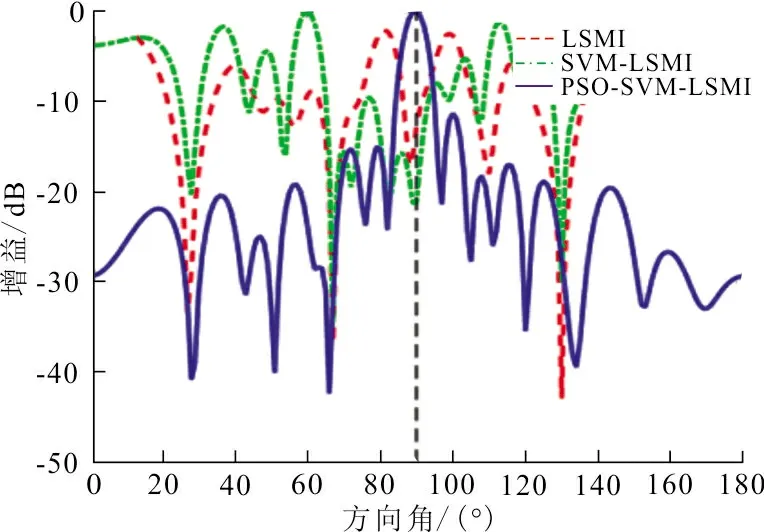
(b) 0.20λ圖 4 SNR為20 dB時不同擾動偏差的波束圖Fig.4 The beam pattern with different disturbance deviation at 20 dB of SNR

從圖4(a)、(b)可以看出，在SNR較高的條件下，無論擾動標準偏差為0.02λ,還是0.20λ，均對LSMI算法的性能產生嚴重的影響，已經無法正確分辨期望信號的來波方向，其旁瓣級迅速升高且出現嚴重畸變，該方法完全失效。對于SVM-LSMI算法，當擾動偏差為0.02λ時，仍然能準確分辨期望信號的來波方向，但旁瓣級在一定程度上升高且發生畸變，當擾動偏差為0.20λ時，該方法的性能完全失效。而PSO-SVM-LSMI算法在擾動偏差為0.02λ時，算法性能依然很穩定，受擾動偏差的影響并不明顯，波束圖效果理想；在擾動偏差為0.20λ時，雖然波束圖的旁瓣發生一定程度的畸變，抑制干擾的能力伴隨著擾動偏差的增大而有所減弱，但仍能夠有效抑制干擾，且具有準確辨別主瓣方向的能力。這充分說明在高SNR的條件下，PSO-SVM-LSMI算法的魯棒性足以保證算法性能的基本穩定。

4 結 語

針對導向矢量存在失配的非理想情況，將SVM理論應用于傳統對角加載波束形成算法中，采用PSO算法求解標準支持向量回歸波束形成優化模型。分別對無失配的理想情況、存在陣元位置擾動和存在波達方向估計失配這3種情況進行仿真分析。仿真結果表明：無論存在失配與否，當陣列對空間中的信號存在響應誤差時，所提方法對其抑制的效果更好，具有很強的魯棒性。