基于雜波擴展的STAP投散射干擾方法

王 坤,張劍云,周青松

(國防科技大學電子對抗學院，合肥，230037)

與地面雷達相比，機載預警(AEW)雷達系統在提供連續偵察和監視方面具有很大的優勢。但機載雷達波束對地面的下俯角較大，使得雷達接收到的雜波功率很大。此外，運動引起的雜波譜多普勒展寬導致對低多普勒目標的可檢測性下降。空時自適應處理(STAP)通過隱式平臺運動補償實現最優雜波抑制，在AEW雷達系統中得到了廣泛應用[1-5]。在電子對抗領域，對STAP的干擾是一個越來越受關注的研究課題，薛冰心等人基于線性調頻信號距離和多普勒頻移的耦合關系研究了頻移假目標干擾[6]，秦兆銳等人研究了移頻靈巧噪聲干擾[7]，沈佳琪等人研究了間歇采樣轉發干擾[8]，趙燕慧等人研究了延時混疊轉發干擾[9],李驥陽等人研究了基于間歇采樣的卷積調制干擾[10-11]，張嘉曦研究了延遲轉發干擾[12]，諶詩娃等人研究了投散射式偽雜波干擾[13-14]，這些干擾方法均為相干干擾，需要對雷達信號進行截獲和采樣，其中投散射式偽雜波干擾明確了采用干擾機主瓣對準雷達主瓣的方式來截獲雷達信號，而其它幾種干擾方法并未說明。考慮到AEW雷達應用的超低副瓣技術，若干擾機作為單獨平臺，這幾種干擾方法應該也是采用主瓣對主瓣的方式來截獲雷達信號，這使得干擾機本身被雷達發現的概率大增。根據干擾路徑的不同，這些干擾可以分為直接路徑干擾和多路徑干擾。頻移假目標干擾、間歇采樣轉發干擾、延遲轉發干擾都是直接路徑干擾，干擾波束需要指向雷達。投散射式偽雜波干擾則是一種多路徑干擾，干擾機主瓣對準地面，利用地物散射特性和雷達、干擾機、地面運動特性產生類似雜波的干擾信號，通過地面散射進入雷達主瓣以達到干擾效果，當干擾機本身在雷達主瓣內時，這種干擾方法功率利用效率不如直接路徑干擾。

本文結合兩類干擾方法的優點，提出一種基于雜波擴展的STAP投散射干擾方法，干擾機本身不在雷達主瓣內，降低了自身被發現的概率，不對雷達直達信號進行截取和采樣，而是對雷達信號經地面散射的雜波信號進行截取和采樣，由于雜波相當于地面環境對原雷達信號進行調制，保證了與原信號的相干性，經采樣、調制、延時轉發給雷達后能獲得相干增益，利于達到干擾效果。采用投散射的方式，通過選擇合適的投射位置使干擾信號經地面散射進入雷達主瓣，使不在雷達主瓣內的干擾機能對雷達進行主瓣干擾。

1 功率計算

本節主要給出干擾機接收到的雷達直達波功率和雷達雜波功率計算公式。若雜波功率大于直達波功率，則說明對雜波信號而非直達波信號進行截取和采樣具有可行性。

1.1 干擾機接收到的雷達直達波信號功率

機載預警雷達、干擾機和目標的空間配置見圖1，雷達主瓣對準目標，干擾機不在雷達主瓣內。雷達A的飛行高度為HA，與干擾機J距離為RJ，相對于干擾機的方位角為φjr，俯仰角為θjr，發射功率為Prt，工作波長為λ，天線增益為Gr(φ,θ)。干擾機飛行高度為HJ，天線增益為Gr(φ,θ)，相對于雷達的方位角為φrj，俯仰角為φrj，則根據基本雷達方程，干擾機接收到的雷達直達波功率為：

(1)

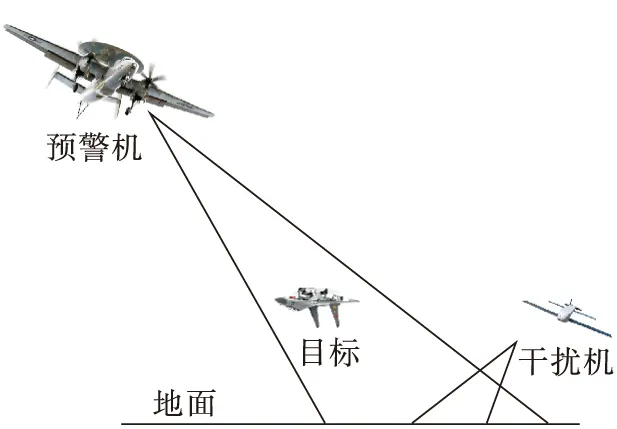
圖1 雷達、干擾機、目標配置圖

1.2 干擾機接收到的雷達雜波信號功率

干擾機除了接收到雷達直達波外，還能接收到經地面散射的雷達雜波信號。滿足到雷達和干擾機的距離之和相等的散射點在空間中形成若干個橢球，它們與地面相交形成若干個橢圓，即干擾機接收到的雷達雜波等距離環。下面以距離之和為R的橢球為例，通過選擇合適的坐標系，求出橢球與地面相交形成的雜波等距離環的解析表達式。

圖2 雷達、干擾機幾何配置圖

如圖2所示，以雷達地面投影點A′為原點，雷達、干擾機連線的地面投影為軸，AA′為軸，垂直AA′和JJ′所在平面作y′軸建立坐標系。以雷達和干擾機連線為軸，連線段中點為原點o，在AA′和JJ′所在平面內作軸垂線為軸，平行于y′軸作y軸建立坐標系，則在坐標系中橢球為標準橢球，其長軸為R，焦距為RJ，其方程為：

(2)

通過旋轉和平移可以得到在坐標系中通過地面某散射點(xi,yi,0)的橢圓方程為：

(3)

通過將式(3)展開為二元二次方程的形式：

(4)

可以將橢圓的半長軸a、半短軸b分別表示為：

(5)

其中：

(6)

圖3 雜波等距離環示意圖

雜波等距離環如圖3所示，內側橢圓即為式(3)表示的橢圓，外側的不規則形狀則是由干擾機接收機分辨單元所形成的，這些分辨單元將整個雜波環分為m塊，其中第i塊雜波塊P的面積即為圖3中陰影部分所示，φji為P相對于干擾機投影點J′的方位角，φ1和φ2由干擾機波束寬度φjB決定，滿足：

(7)

以J′為原點建立極坐標系，可以將橢圓方程改寫為：

(8)

式中：rj為雷達干擾機地面投影距離；r(φ)為某雜波塊到J′的距離；φ為其對J′的方位角，用l表示rj+B/2A，可將r(φ)表示為φ的函數形式：

(9)

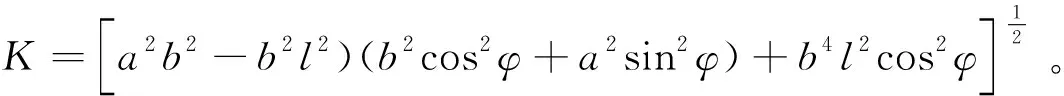
由此，雜波塊P的面積可以用積分表示為：

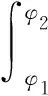
(10)

式中：Δ是干擾機接收機距離分辨單元在地面的投影，Δ=cτsecθji，c為光速，τ為雷達脈沖寬度，θji為P相對于干擾機的俯仰角。根據文獻[15]中給出的表面雜波雷達方程，干擾機接收到雜波塊P散射的功率為：

(11)

式中：φri、θri為P相對于雷達的方位角和俯仰角，φji為P相對于干擾機的方位角；σ0為散射系數；r1為P到雷達的距離；r2為P到干擾機的距離。干擾機接收到該雜波環的雜波總功率為：

(12)

2 信號模型

2.1 干擾機接收到的雷達直達波信號模型

機載預警雷達A、干擾機J和雜波塊幾何配置如圖4所示，雷達以速度vA沿x軸方向飛行，干擾機以速度vJ飛行，飛行方向與x軸夾角為δj。

圖4 雷達、干擾機、雜波塊幾何配置圖

假設雷達發射信號為：

st(t)=Re[AtE(t)ejwct]

(13)

vr=vAcosθrjcosφrj-vJcosθrjcos(φrj-δj)

(14)

干擾機接收到的信號為Re[ArE(t-τ)ejωc(t-τ)]，其中τ=(RJ-vrt)/c，由相對運動產生的多普勒頻移為vr/λ。

2.2 干擾機接收到的雷達雜波信號模型

如圖4所示，雜波塊P到雷達、干擾機的距離之和R2w=r1+r2是隨時間變化的，不妨設t=0時，R2w=R0。在t時刻，干擾機接收到的信號是雷達在t-τ(t)時刻發射的，此時有：

R2w(t-τ(t))=R0-(vAcosφricosθri+

vJcos(φrj-δj)cosθji)(t-τ(t))

(15)

可以解出：

τ(t)≈

(16)

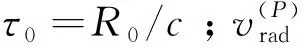
(17)

根據文獻[1]，干擾機接收到的由雜波塊P散射的信號為：

(18)

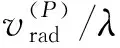
假設雜波回波可等效為NC個獨立雜波塊散射信號之和，由于各信號多普勒頻移不同，各信號是相互獨立的，干擾機接收到的總的雜波信號sjr(t)可以寫為：

(19)

2.3 雷達接收到的干擾信號模型

(20)

式中：fj是干擾機對式(19)表示的接收信號進行調制處理得到的虛假多普勒頻率。機載雷達的天線陣列布局如圖5所示，為線性側視陣列，則干擾機接收的單一散射塊干擾信號的時間相位項和空間相位項分別為：

(21)

圖5 雷達天線陣列布局

加上傳感器方向圖D(φ)，陣列方向圖G(φ,m)，地面反射率L(φ)，那么在第m個時刻第k個傳感器接收到的一個距離單元總的干擾信號為：

jmk=

(22)

3 干擾基本原理

3.1 投散射式偽雜波干擾原理

(23)

fdj可以表示為方位角φri和虛假多普勒頻率fj的函數：

fdj=F(φri,fj)

(24)

由于fdj的方位依存性，偽雜波干擾信號的功率譜與雜波功率譜類似，具有空時二維性，如圖6所示，文獻[14]中將其稱為偽雜波。從圖6(b)可以清楚地看到偽雜波譜占據了所有的方位，通過控制fj可以使偽雜波譜在空時平面上沿多普勒頻率方向平移。

圖6 偽雜波干擾下的功率譜(fj=450Hz)

與雜波相同，偽雜波在單一維度上是無法濾除的。STAP處理器像處理雜波一樣處理偽雜波。偽雜波干擾前、后在40°方位角上的改善因子如圖7所示，可以看到干擾后，不僅了產生一個雜波凹口以濾除雜波，還產生了一個偽雜波凹口以濾除偽雜波。其它方位角上的改善因子圖與此類似。通過調整fj可以使偽雜波譜在空時二維平面上平移進而使偽雜波凹口沿多普勒頻率方向平移，當目標的多普勒頻率fdt和方位角φrt滿足式(24)，即fdt=F(φrt,fj)時，目標被偽雜波凹口覆蓋，STAP處理器在濾除偽雜波的同時將目標也濾除了。

圖7 偽雜波干擾前、后改善因子對比(φrt=40°)

由以上分析可知，要使偽雜波凹口準確覆蓋目標需要知道目標的多普勒頻率、方位角和所在距離單元等先驗信息。這種對先驗信息的高要求是投散射偽雜波干擾方法的最大短板。若干擾指標要求使目標處的響應下降10 dB以上，定義偽雜波凹口寬度D為改善因子-10 dB處對應的歸一化多普勒頻率范圍，則由圖7可知，當目標先驗歸一化多普勒頻率誤差超過D/2時，將不滿足干擾指標要求。

與傳統的轉發式干擾形成具有不同多普勒頻率或不同距離的假目標不同，投散射式偽雜波干擾利用STAP處理器特性將真實目標信息濾除，而傳統轉發式干擾下STAP能同時獲取真實目標和假目標信息，且真實目標與假目標具有相同的方位信息。

3.2 基于雜波擴展的投散射干擾原理

由式(20)可知基于雜波擴展的投散射干擾相當于位于同一位置的NC部干擾機同時進行偽雜波干擾，干擾機的功率PJ需分配到這NC個干擾信號上，每個干擾信號的功率為PJ/NC。干擾后的功率譜如圖8所示，可以看到干擾功率譜相當于將圖6中的偽雜波譜壓扁，將功率分配到更多空時位置上。

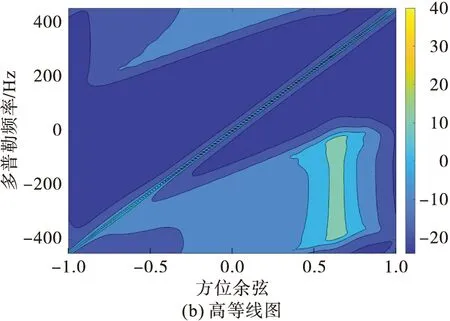
圖8 基于雜波擴展的投散射干擾下的功率譜(fj=450Hz)

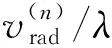
(25)

干擾前、后在40°方位角上的改善因子如圖9所示，可以看到干擾后，在雜波凹口外還產生了一個很寬的干擾凹槽，當目標落入該凹槽時，其響應下降將超過25 dB，從而能達到干擾要求。對比圖7可以看到相比于偽雜波干擾，基于雜波擴展的投散射干擾大大降低了對目標先驗信息準確性的要求。

圖9 基于雜波擴展的投散射干擾前、后改善因子對比

4 仿真實驗

本節主要通過仿真實驗比較干擾機接收到的雷達直達波功率和雷達雜波功率，驗證截獲雷達雜波而非雷達直達波的可行性。通過與偽雜波干擾進行仿真對比驗證所提干擾方法的有效性。雷達系統參數由表1給出。

表1 雷達系統參數

基于雜波擴展的投散射干擾將功率分配到NC個子干擾信號上，不妨按角度將NC設為360。干擾機發射功率Pjt為500 W，干擾機發射增益Gjt為18 dB，干擾機天線后瓣增益Gjb為-30 dB，雷達天線陣元和干擾機天線均采用余弦方向圖，雷達天線陣元合成的波束指向目標，干擾機天線指向目標所在方位上的偽雜波塊，運動平臺參數由表2給出，經計算可知目標多普勒頻率為-60.041 5 Hz,方位余弦為0.766。

表2 運動平臺參數

4.1 功率比較

圖11比較了RJ=120 km時干擾機收到的雷達直達波功率和不同地形條件下的雷達雜波功率。隨著R2w增大雷達雜波功率減小，由于對偶性，干擾功率也會隨著R2w增大而減小，因此選擇投射位置時應使R2w盡可能小，此時在幾種地形條件下雜波功率均大于直達波功率。這驗證了截獲雷達雜波信號而非雷達直達波信號的可行性。

圖10 指定R2w下直達波和雜波功率比較

圖11 指定RJ下直達波和雜波功率比較

4.2 干擾效果對比

圖12是2種干擾條件下雷達STAP處理器目標方位上改善因子的對比，可以看到偽雜波干擾在目標所在的多普勒頻率處形成了一個窄而深的凹口，使目標的響應下降了40 dB。基于雜波擴展的投散射干擾則以目標多普勒頻率為中心形成一個寬而較淺的凹槽，使寬約0.4歸一化多普勒頻率(記為F)的多普勒頻率范圍上的響應均下降了25 dB左右。

圖12 干擾后雷達STAP改善因子對比

圖13和圖14分別是2種干擾后雷達STAP最優響應。圖13中偽雜波干擾后，偽雜波凹口覆蓋目標，使目標處響應極低，目標多普勒信息和方位信息均被濾除。

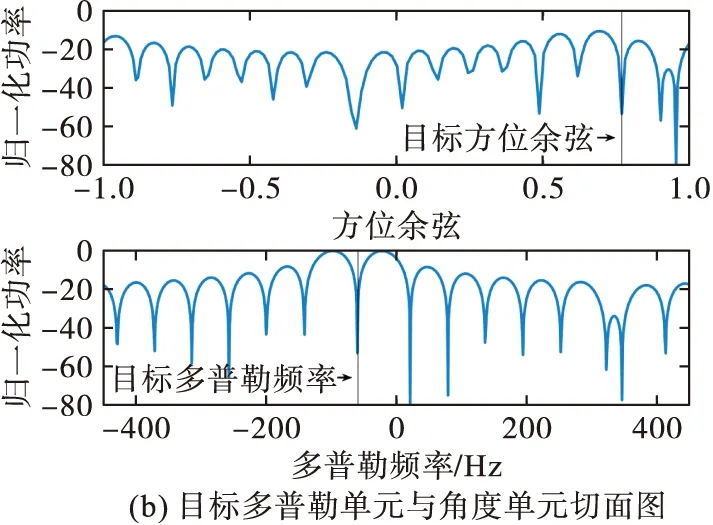
圖13 偽雜波干擾后STAP最優響應

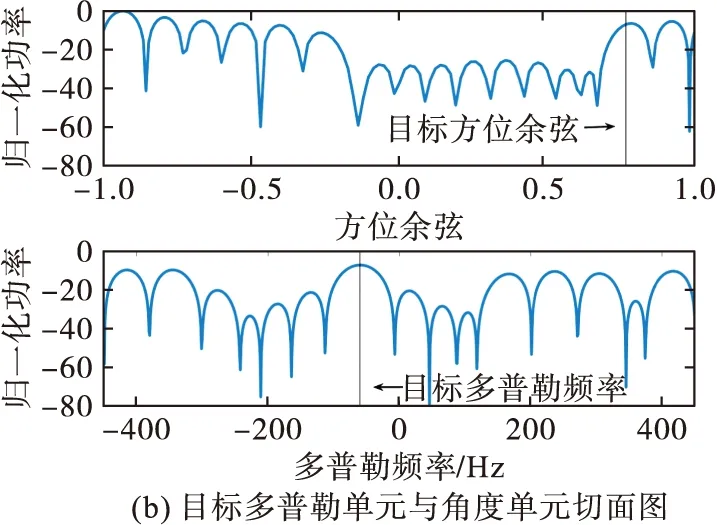
圖14 基于雜波擴展的投散射干擾后STAP最優響應

從圖14(a)可以看到基于雜波擴展的投散射干擾在目標空時位置附近形成了一個很寬的凹槽，使凹槽內的響應均下降，從圖14(b)可以看到干擾后雖然目標處響應仍能取得峰值，但已經不是唯一的峰值，相當于形成了若干假目標，與頻移假目標干擾僅能形成多普勒頻率上的假目標不同，基于雜波擴展的投散射干擾在方位上也形成了假目標。

從干擾效果來看，偽雜波干擾無疑優于基于雜波擴展的投散射干擾，但偽雜波干擾對先驗信息準確度要求較高，圖15和圖16分別是目標先驗多普勒頻率信息誤差0.03F時2種干擾條件下的STAP最優響應，對比圖13和圖14可以看出基于雜波擴展的投散射干擾的效果沒有變化，而偽雜波干擾效果明顯變差，因此，從對目標先驗信息誤差容錯性方面，基于雜波擴展的投散射干擾要優于偽雜波干擾。

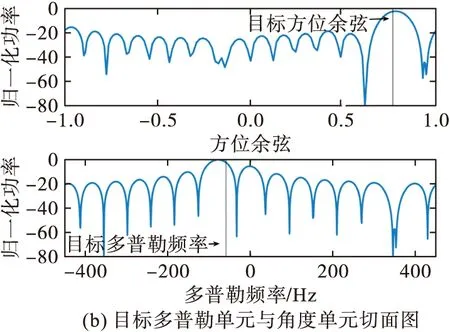
圖15 偽雜波干擾后STAP最優響應(誤差為0.03F)

圖16 基于雜波擴展的投散射干擾后STAP最優響應(誤差為0.03F)

5 結語

本文研究了一種基于雜波擴展的STAP干擾方法。在雷達信號截獲方面，對雷達雜波而不是直達波進行截獲，解決了在雷達主瓣截獲直達波信號被發現概率較大的問題，且雜波信號相當于地面環境對原雷達信號進行了一次調制，保持了相干性，能夠獲得相干增益，通過仿真比較了干擾機接收到的雷達雜波和直達波的功率，驗證了可行性。在干擾時，采用投散射的方式，在雷達副瓣內通過地面散射的方式使干擾信號進入雷達主瓣，形成一個很寬的干擾凹槽，相比于偽雜波干擾，對目標先驗信息準確性要求較低，更容易覆蓋目標，使目標響應下降，不再是空時平面上的唯一峰值，達到在方位和多普勒頻率上均形成假目標的效果。仿真結果驗證了這種干擾方法的有效性。在實踐中，由于目標準確先驗信息并不容易獲得，因而基于雜波擴展的投散射干擾較偽雜波干擾更實用，當進一步增加干擾功率時，可以在很寬的頻率范圍內達到偽雜波干擾的效果。

本文中的干擾方法主要針對傳統的STAP技術、考慮到壓縮感知理論在STAP中的應用日益增加[15-20]，下一步將展開該干擾方法時稀疏恢復STAP技術的干擾效果。