一類帶時變系數的退化拋物系統的奇性
胡 麗, 樊明書
(西南交通大學數學學院, 成都 610031)
1 引 言
在本文中, 我們研究以下的方程組:
(1)
其中Ω?Rn是一個光滑有界區域,m,n>1, 系數k1(t),k2(t)是關于t>0的正連續函數. 我們假設非線性項f1(v),f2(u)滿足f1(v)>0,f2(u)>0,f1′(v)>0,f2′(u)>0,(u,v>0),f1(0)=f2(0)=0,且初值u0(x),v0(x)是非平凡的非負連續函數, 在邊界?Ω上為零.
自上世紀60年代以來, 很多學者對非線性拋物方程的整體解和爆破進行了研究[1-6].如,2007年Payne等[7]研究了帶Dirichlet邊界條件的下述半線性拋物問題
ut=Δu+f(u), (x,t)∈Ω×(0,t*),
證明了該方程存在爆破解, 并對爆破時間進行了估計.2016年, Xia等[8]研究了半線性拋物方程
ut=Δum+f(t)g(u), (x,t)∈Ω×(0,T),
其邊界條件為u(x,t)=0,(x,t)∈?Ω×(0,T),證明了解的全局存在性, 解在有限時間內爆破, 并給出了爆破時間的上下界估計. 同年,Xia等[9]研究了方程組的相似情形. 其它的相關工作還可參見文獻[10-13].
另一方面,在文獻[5]中, Du給出了擬線性退化方程(組)爆破解的處理方法. 受此啟發, 我們利用該文中的方法對問題(1)進行研究. 我們將首先建立(1)的局部存在性和比較原理,在此基礎上給出(1)的整體存在和爆破的條件. 我們的主要結果如下.
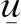
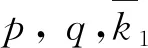
定理1.3假設存在正常數p,q及ξ>0使得f1(ξ)≥ξp,f2(ξ)≥ξq成立, 且k1=min{infk1(t),infk2(t)}>0. 若pq>mn, 則問題(1)的每個古典解對大的初值u0(x),v0(x)在有限時間內爆破.
2 比較原理
在本節中我們證明定理1.1.固定ε>0并定義u0,v0為
u0=u(x,0)+ε,v0=v(x,0)+ε
(2)
對n=1,2,3,…, 歸納定義un,vn為下述問題的解:
(3)
容易看出,un≤un-1,vn≤vn-1(n=1,2,…). 對n=1, 該不等式是我們的假設. 換言之, 我們假設u0≥u1,v0≥v1. 設該不等式對n-1成立, 即
un-1≤un-2,vn-1≤vn-2.
那么
un-1,t-Δun-1(x)m-k1(t)f1(vn-1)≥
un-1,t-Δun-1(x)m-k1(t)f1(vn-2)=0,
vn-1,t-Δvn-1(x)n-k2(t)f2(un-1)≥
vn-1,t-Δvn-1(x)n-k2(t)f2(un-2)=0,
un-1(x,0)≥un(x,0),vn-1(x,0)≥vn(x,0).
因而(un-1,vn-1)是問題(3)的一個上解,從而
un≤un-1,vn≤vn-1.
定義
當IΩ(u,v,χ)=JΩ(u,v,χ)=0時,我們稱(u,v)是(1)的弱解.
設η滿足
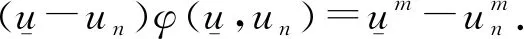
且
因此
同理,
這意味著
3 整體解的存在性
為了后面證明方便, 我們首先不加證明地引入下邊兩個引理.記
引理3.1若pq
引理3.2若pq>mn, 則存在正常數l1,l2使得AL<(0,0)T且A(cL)<(0,0)T對所有c>0成立.
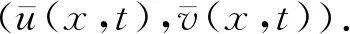
設φ(x)是
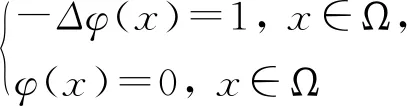
(4)
(5)
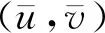
(1+φ(x))ml1-2|φ(x)|2+
(1+φ(x))ml1-1Δφ(x)}≥
-ml1Kml1(1+φ(x))ml1-1Δφ(x)=
ml1Kml1(1+φ(x))ml1-1≥
ml1Kml1(1+C)ml1-1
(6)
(7)
類似可得
nl2Knl2(1+C)nl2-1
(8)
及
(9)
其中
(10)
若pq
(K(φ(x)+1))l1≥u0(x),
(K(φ(x)+1))l2≥v0(x)
(11)
4 解的有限時間爆破
在定理1.3的證明中,我們采用Du在文獻[5]中的證明思想.
首先,由比較原理, 我們構造問題(1)在Ω的某個子區域內的上解, 其中u,v>0.
設ψ(x)是一個平凡的非負連續函數且在?Ω上為零. 不失一般性, 我們假定0∈Ω且ψ(0)>0. 接下來, 我們構造問題(1)的一個爆破上解. 記
(12)
其中
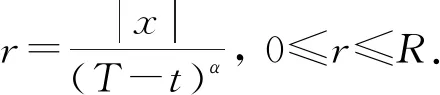
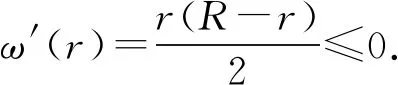
對充分小的T,記

B(0,R(T-t)α)?B(0,RTα)?Ω
(13)
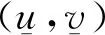
(14)
且
(15)
其中T>0充分小.
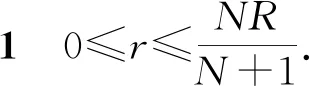
(16)
(17)
從而
(18)
(19)
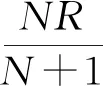
(20)
(21)
如果pq>mn, 由引理3.2知存在兩個正常數l1,l2, 使得
ml1-pl2<-1,nl2-ql1<-1,
(m-1)l1>1, (n-1)l2>1.
這樣,我們得到
pl2>ml1+1>l1+1,ql1>nl2+1>l2+1
pl2>ml1+1>l1+1,ql1>nl2+1>l2+1.
因此, (13)式對充分小的α>0和T>0成立. 應用式(18)~(21)得
(22)