有吹吸速度的外掠多孔平板湍流邊界層的積分方法

李開勇, 趙 波, 王翼鵬, 王梓羽

(四川大學機械工程學院 教育部空天動力燃燒與冷卻工程研究中心， 成都 610065)

1 引 言

航空航天等技術的迅猛發展對飛行器表面和發動機壁面的高效熱防護性能提出更苛刻的要求，例如火箭發動機壁面和高速飛行器表面的發散冷卻和航空發動機渦輪葉片的氣膜冷卻技術一直受到廣泛關注[1-5]. 此外，質子交換膜燃料電池在燃料輸運過程中需經過具有多孔壁面的雙極板通道并經擴散層到達膜電極處進行化學反應發電. 上述應用均可歸結為壁面具有吹吸速度的外掠平板邊界層流動問題[6]. 本文主要限于多孔壁面的湍流速度邊界層理論研究. 目前，外掠多孔平板層流邊界層的理論研究相對較多，且多采用積分法或通過相似變換對動量和能量微分方程進行求解：Thomas等[7-8]采用多項式描述速度和溫度分布，利用積分法獲得了多孔壁面層流邊界層的速度和溫度場；Afzal[9]利用冪函數代表速度并通過積分法和變量替換，將Falkner-Skan控制方程轉換成常微分方程以得到速度場分布；Watanabe等[10]通過引入新變量，將控制方程簡化為耦合非線性微分方程求得具有滲透表面圓盤的速度和溫度場. 由于湍流機理的復雜性[11-15]，湍流邊界層動量和熱量傳遞的試驗研究常常先行于理論[16-19]，此外還采用數值仿真的方法[20-22]，目前驗證湍流理論模型的基準試驗數據多來自Kays院士及其合作者[23].

當前，外掠平板湍流邊界層的理論研究多采用量綱分析的比擬法、漸近分析方法和積分方法建立雷諾時均動量方程(RANS)和能量方程[24-28]，其中湍流運動粘度和湍流熱擴散率的確定主要遵循普朗特混合長度理論. Vigdorovich[25-26]針對外掠可滲透壁面湍流速度邊界層問題，采用漸近分析和無量綱比擬的方法建立了雷諾時均N-S方程，但需以相同條件下的非滲壁面速度分布作為已知條件. Khademi等[27-28]將湍流速度和溫度邊界層劃分為層流底層和湍流核心區，兩個區域均采用多項式代表速度或溫度分布，最后采用積分方法獲得湍流邊界層的速度和溫度場分布，但他們的研究只限于非滲透壁面情況. 本文將在課題組前期非滲透壁面研究基礎上[29]，集中討論具有吹吸速度的可滲透表面湍流速度邊界層的分布，擬分別采用三次多項式和1/5次冪函數代表層流底層和湍流核心區的速度分布，利用積分方法建立湍流邊界層動量方程，最終獲得速度場的解析解. 該方法與現有試驗結果及經驗公式符合得較好，而且具有形式簡潔和求解時收斂迅速等優點.

2 理論模型

2.1 利用積分方法建立動量方程

如圖1，將外掠多孔平板湍流速度邊界層劃分為層流底層和湍流核心區[27-28]，u∞為主流區恒定流速，υs為垂直滲透壁面、均勻分布且不變的吹入或吸出速度，δ1和δ分別為湍流速度邊界層的層流底層厚度和總厚度(即層流底層加湍流核心區的厚度). 假設：流體不可壓縮且物性參數均為常數；湍流流動是定常的，即流場各位置的時均速度不隨時間變化；主流區速度和壁溫為常數；不考慮轉捩區，認為湍流從層流末端開始，該臨界位置(x=0)處湍流速度邊界層總厚度δ等于該位置層流速度邊界層的厚度δ*，而層流底層厚度δ0極薄，參考Khademi[27-28]假設，這里視δ0為一個無限接近零的正數，文獻[29]中對非滲透表面的研究中已表明這種處理能夠保證理論模型的預測精度，取臨界雷諾數Re=5×105[27-28]，如圖1.

湍流邊界層的雷諾時均動量方程為[23]

(1)

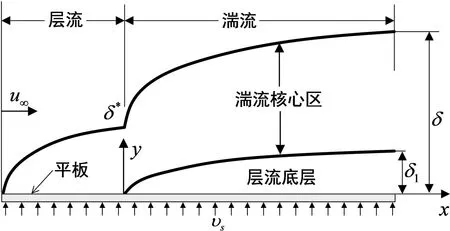
圖1 外掠可滲透平板湍流速度邊界層示意圖

圖2給出湍流流動控制體積示意，區域1-2-3-4為層流底層，3-4-5-6為湍流核心區，l為流體厚度，dx為x向微元. 因dx極小，認為湍流邊界層的層流底層厚度δ1在dx內沿x向不變. 根據動量守恒定理，采用與層流邊界層類似的積分方法[23]，最后獲得多孔平板的湍流動量積分方程為

(2)

式中μ為流體的動力粘度，u1和u2分別為層流底層和湍流核心區的速度，uL為層流底層外緣處速度. 此外，相應邊界條件為：

u1|y=0=0,u1|y=δ1=u2|y=δ1,

圖2 外掠可滲透平板湍流控制體積示意圖

2.2 速度分布函數

認為外掠多孔壁面湍流邊界層的速度具有相似的速度分布，在非滲透壁面的研究基礎上，采用三次多項式和1/5次冪函數分別代表層流底層和湍流核心區的速度分布[29]，即

(3)

由上述邊界條件確定式(3)的待定系數為

a1=0，

a5=u∞δ-1/5.

這里，定義壁面吹吸雷諾數Res=υsδ1/v=Fu∞δ1/ν，F為吹風比. 代回速度分布函數式(3)，則可滲透表面平板湍流邊界層的速度表達式如下

(4)

2.3 積分方程組求解

3 結果討論

3.1 湍流速度場的理論分布

圖3和圖4分別給出具有噴注(吹入)和吸出速度的外掠平板湍流邊界層速度分布情況，圖中 “IDENT”指1968年斯坦福大學 AFOSR 大會所采用的那套實驗數據，本文解析解分別與Whiten試驗和Blackwell的試驗結果[23]進行了對比，其中吹風比F=υs/u∞，F>0代表噴注，F<0為吸出. 由圖可見，在層流底層理論解與試驗值符合得較好，而在湍流核心區雖存在一定偏差，但大體趨勢是符合的，最大相對誤差6%. 理論和試驗結果存在一定偏差的主要原因是：就作者所知，以往外掠多孔壁面湍流試驗中，與本文常自由速度和常壁溫條件完全相同的試驗尚未發現，在文獻[23]收集的試驗數據中，Whiten的試驗條件(IDENT 62067)是零壓力梯度加變化的壁溫，即混合邊界條件，這與本文前面的常自由速度和常壁溫假設不完全一致；而Blackwell的試驗條件(IDENT 122371)是常壁溫和逆壓力梯度(即u∞隨x是減小的)，也與本文理論模型的假設有所差別. 求解理論模型時由于可滲透壁面湍流模型的復雜性，需用數值方法聯立求解動量和能量積分方程組，求解結果與常壁溫條件相關. 關于外掠多孔平板湍流溫度邊界層和三維熱對流密度函數的理論模型，將另文報道.

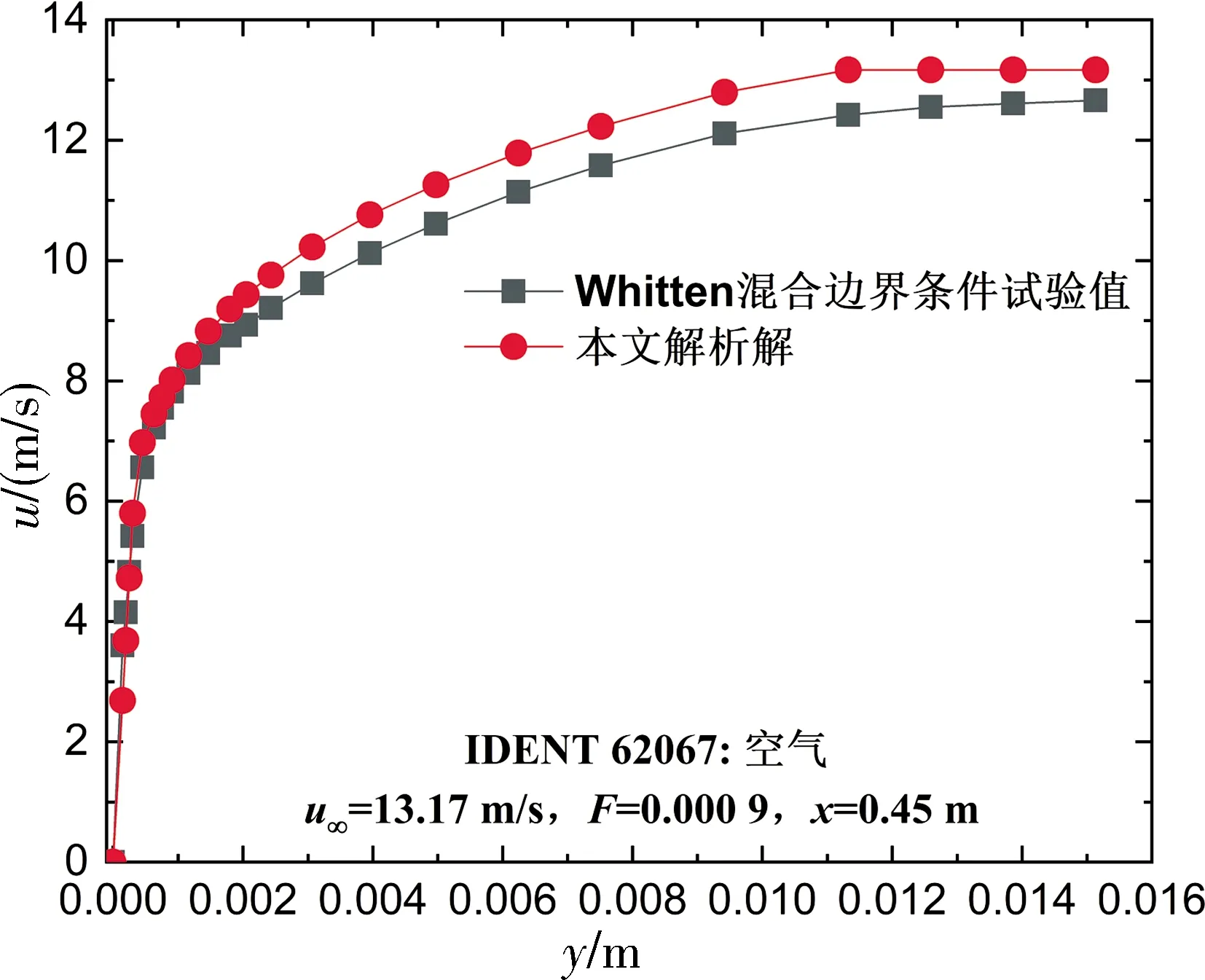
圖3 本文速度解析解與Whitten試驗結果比較

圖4 本文速度解析解與Blackwell試驗結果比較

圖5給出吹風比F變化時主流方向速度u的分布規律. 注意到在流體厚度y保持不變時，隨著吹風比F的增加，x方向的流體速度隨之增大. 由圖可見，與沒有壁面吹吸速度(F=0)時相比，當通過壁面吸出流體(F<0)時，速度邊界層δ會變薄，而流體吹入(F>0)時δ相應變厚，吹入速度υs增大到一定數值會最終導致邊界層分離，這些與Schlichting等人[12]以及Kays等人[23]試驗結論一致.

3.2 摩擦系數的理論預測

圖5 吹風比F變化時速度場的理論分布

圖6 理論解確定的摩擦系數與Kays經驗公式對比

4 結 論

本文主要研究具有吹吸速度壁面外掠平板湍流邊界層速度場問題，利用積分方法建立了湍流動量方程，并獲得湍流速度場和壁面摩擦系數的理論分布. 首先將湍流邊界層劃分為層流底層和湍流核心區兩部分，然后分別采用三次多項式和1/5次冪函數對速度分布進行描述，隨后用積分法建立了動量積分方程，最后用四階龍格-庫塔算法求解得到湍流速度場的解析解，同時獲得壁面處的摩擦系數. 邊界層速度理論解分別與Whitten和Blackwell的試驗結果以及Kays的多孔壁面湍流經驗公式對比表明，最大相對誤差為6%，摩擦系數與Kays經驗公式的最大相對誤差為4.9%. 這些工作為后續發散冷卻壁面條件下湍流溫度場和對流傳熱特性的理論研究奠定了較好基礎.