基于SHAW模型的山西沁河流域水資源配置方法研究

趙電雷

(晉城市水務局水利水電事務中心，山西 晉城 048000)

0 前 言

目前常用的水資源配置方法有基于改進果蠅算法[4]和基于地下水“雙控”2種水資源配置方法[5]。但上述方法計算得到流域產流損失數值較小，易導致水資源出現供需失衡的情況。SHAW模型最初用于模擬土壤凍融過程，研究凍融過程水分的遷移，經過研究人員不斷地改進，SHAW模型可實現對循環系統中多種物理指標的模擬，并整合多指標的物理性質形成垂向的一維剖面，在該剖面內建立一個生物分層系統，描述剖面的水通量，從而能夠更加準確得到流域周圍土壤成分中水分的變化。

山西沁河流域發源于長治市沁源縣霍山南麓的二郎神溝，屬于黃河的一級支流，位于太行山脈西側，地形北高南低，大部分流域為海拔700 m左右及以上的海拔高度的山區，支流數量眾多[1]。由于地勢原因，沁河的徑流大多由降水形成，降水一部分形成地表水匯入河道中，另外一部分滲入地表下形成地下水[2-3]。為此，本文研究利用SHAW模型，結合沁河流域的自然環境，提出1種山西沁河流域水資源配置方法，因地制宜的調度沁河流域的水資源，合理配置水資源，改善沁河的水生態環境。

1 水資源配置方法研究

1.1 SHAW模型處理流域下邊界水熱通量

由于沁河流域的特殊地理位置及特殊的土壤剖面，故采用SHAW模型處理流域下邊界水熱通量。考慮到沁河流域海拔過高，存在部分土壤凍結融化的過程，首先計算該過程中土壤內的水通量，計算過程如下：

(1)

式中：θl為土壤體積內含水率變化；θi為土壤體積內含冰率變化；t為時間；ρi表示進入土層的液態水通量；ρl為進入土層的氣體通量；z為土壤深度；h為土壤基質勢；k為土壤導水率；qv為土壤內水分蒸發所需的熱量；U為根系吸水源系數。在此基礎上，根據水通量計算結果，采用BC模型描述流域周圍土壤水分特征，描述公式可表示為：

(2)

式中：he為進氣值;θsat為孔隙含水量;b為土壤孔徑分布參數。當沁河流域土壤凍結的情況下，假定該部分凍土水分位于非飽和土壤中，土壤孔隙的基質勢不變，導水率受到冰量的影響，導水率逐漸減小直至為零，此時土壤內的有效孔隙率為0.13[6]。但土壤孔隙中存在部分的溶質勢，孔隙內溫度在凍結溫度之下，土壤孔隙內部的液態水與冰處于平衡狀態，故得到土壤總土水勢與溫度間的關系，如下：

(3)

式中：E為土壤總土水勢;R為溶質勢，Lf為溶質水的凍結潛熱，g為重力加速度，Tk為冰量轉化為溶質的時間，其余參數含義保持不變。根據上述數值結果，計算得到溶質勢數量關系：

(4)

式中：c為土壤水質中溶質濃度;A為氣體常數。根據上述得到的土壤液態水含量，假設沁河流域土壤內大于含水量部分的水分以冰形態存在[7]，考慮到冰在融化時吸收的熱量，沁水流域周圍的溫度分布就可表示為：

(5)

式中：Cs為體積熱容量;T為水域土壤溫度;ql為液態水通量;cl為水的比熱容，其余參數含義不變。部分土壤中水溶質存在部分的植物吸收，計算溶質在流域土壤內的吸收系數，計算過程如下：

(6)

式中：Dw為溶質的濃度;τ為土壤迂曲度參數。綜合上述SHAW模型處理過程，流域土壤含水量及土壤溫度可根據不同沁河流域的季節改變，模型可自行對流域土壤含水量及溫度進行線性處理，得到不同季節時間點下沁水流域下邊界熱量變化[8]。

根據下邊界數值結果，采用SHAW模型模擬得到整條沁水流域含有水力梯度的重力梯度，進而得到沁水流域土壤底部溫度[9]。根據溫度變化值，得到沁水流域外部降水部分轉化為地下水的含量，便于合理化配置沁水流域水資源。

1.2 山西沁水流域可配置水資源調度量計算

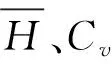
(7)

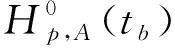
(8)

式中：Kp為模比系數;Hp為點暴雨均值。計算得到定點雨量的計算結果如表1所示。

參照上表所得到的各項數值，得到面暴雨的計算公式，如下：

(9)

式中：Hp,A(tb)為設計面暴雨；ηp(A,tb)為點面折減系數，可按下式計算：

(10)

式中：A為流域面積;C，N均為經驗參數。整理得到設計面的暴雨計算公式：

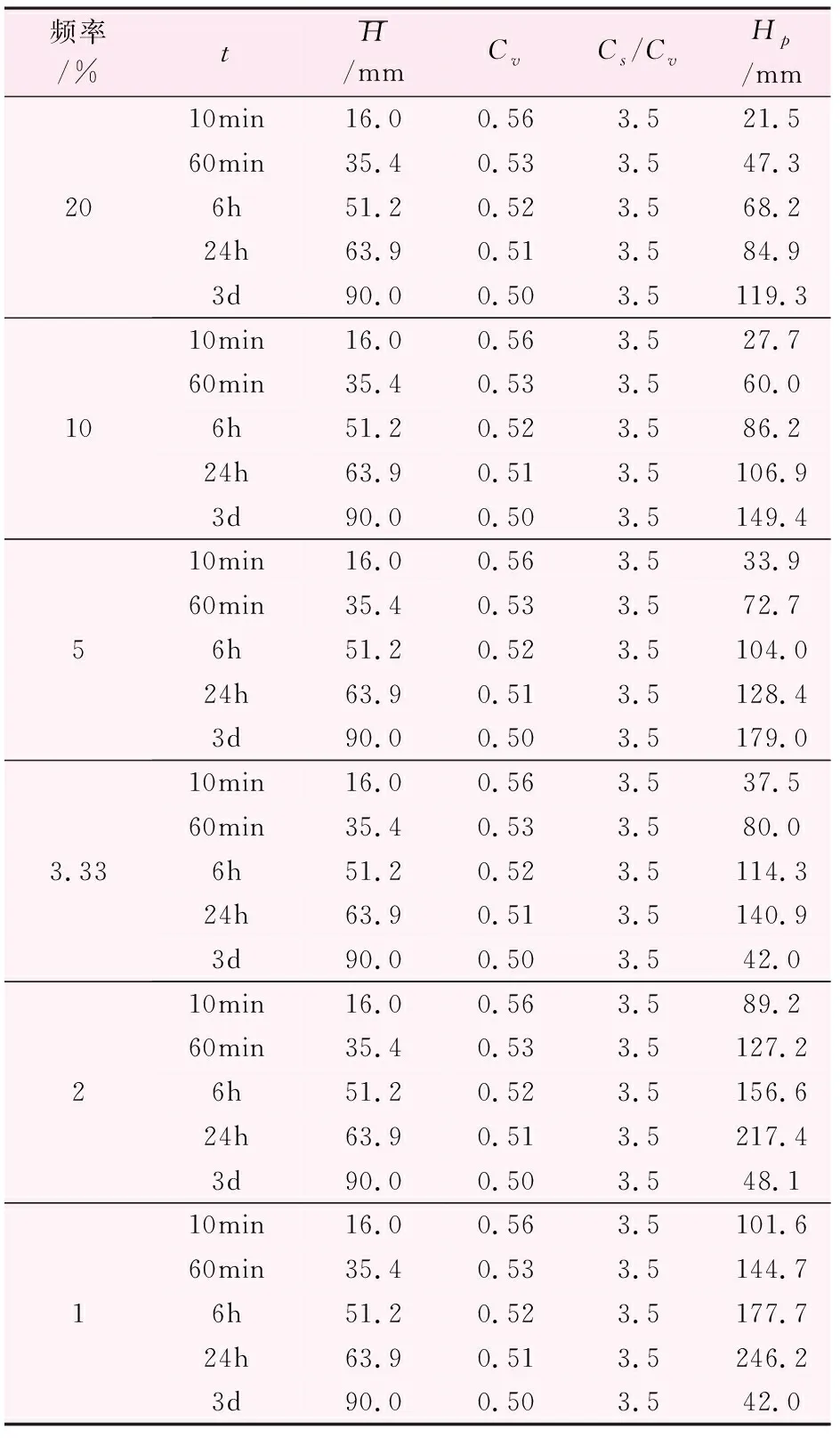
表1 設計定點雨量計算結果表

(11)

式中：Sp為設計雨力，即1 h的設計雨量;λ為經驗參數;ns為設計面雨量修正值。在此基礎上，計算山西沁河流域產流，計算過程如下：

(12)

式中：tanh為雙曲正切運算符;tZ為設計暴雨的主雨歷時;Rp為設計洪水凈雨深;FA(tZ)為主雨歷時內的流域可能損失。根據該部分流域的可能流失，得到該時段下凈雨量，計算公式如下：

Δhp,j=hp(tj-1+Δt)-hp(j-1)

(13)

式中：hp(t)為設計時段凈雨深;Δt為雨量計算時段;j為雨量流失時間段。綜合沁水流域內的調度量作為總配置量[11]，實現山西沁河流域水資源的的合理配置。

1.3 實現水資源配置

應用上述得到的可配置調度量，采用綜合瞬時單位線法進行匯流計算，量算各匯流地類面積占流域面積的權重，根據權重值計算沁水流域洪水過程線，過程線計算公式如下：

(14)

式中：J為河道比降;C1,A為復合地類匯流參數;C1,i為單地類匯流參數;β為經驗性指數;α為面積權重。根據上述計算出的數值，得到書院河段的洪峰流量及最大24 h洪量值，結果如表2所示。

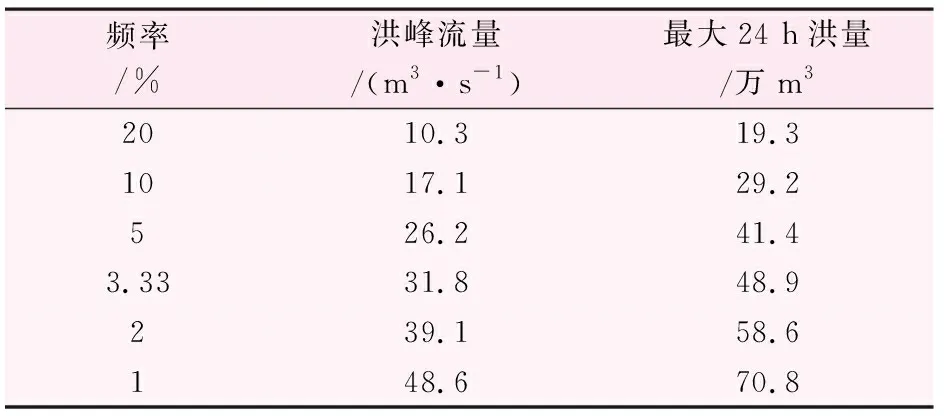
表2 洪峰流量及最大24 h洪量值表

以沁水流域洪水過程線內的水資源作為分配指標，預測山西省對沁水流域的需水情況時，以沁河流域人口分布情況作為配置依據[12]，見表3所示。

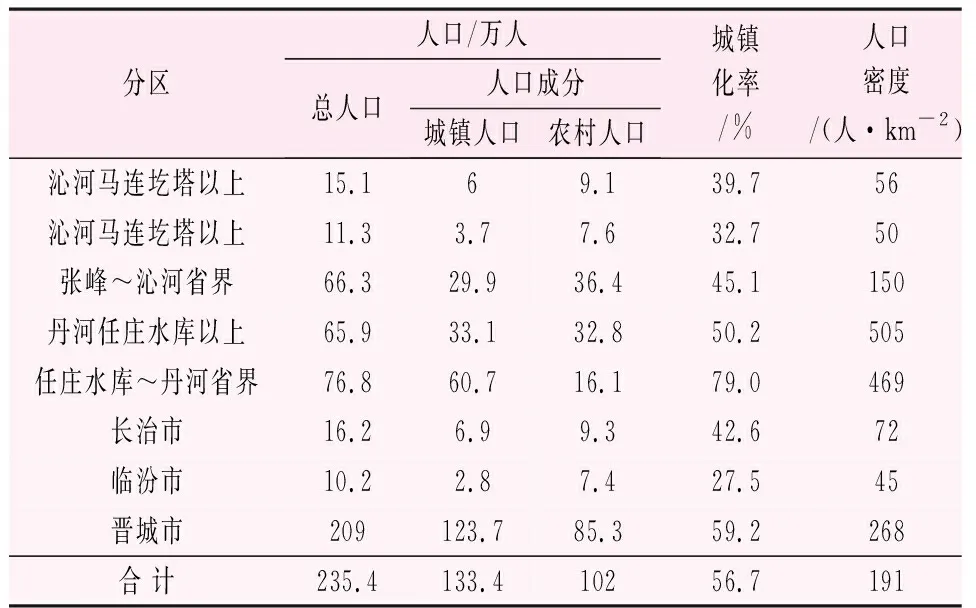
表3 沁河流域現狀人口分布情況表

按照表3所示的人口成分，綜合區域內城鎮化的情況，將人均用水量定額為200 L/人·d，參照城鎮與農村人口的數量預測得到沁河流域配置的生活需水量[13]。利用表3中農村人口數量，認定當前山西沁河流域周圍的耕地面積不變。根據沁河流域產業分布情況，確定3項產業的水資源需求以及產業分布情況，結果如表4所示。

使用表4所示的產業分布，在考慮農業節水灌溉技術水平的同時，利用第一產業占比數值，查閱歷史資料的農業用水來配置沁河的水資源[14]。由于工業、建筑業需水受到行業結構、生產技術等外部因素的影響，該行業配置水資源存在較大不確定性，故將一個工作單位作為計算單位，每個單位分配可用于一周日常工作活動的預算水量[15]。同理配置得到第三產業配置得到的水資源。

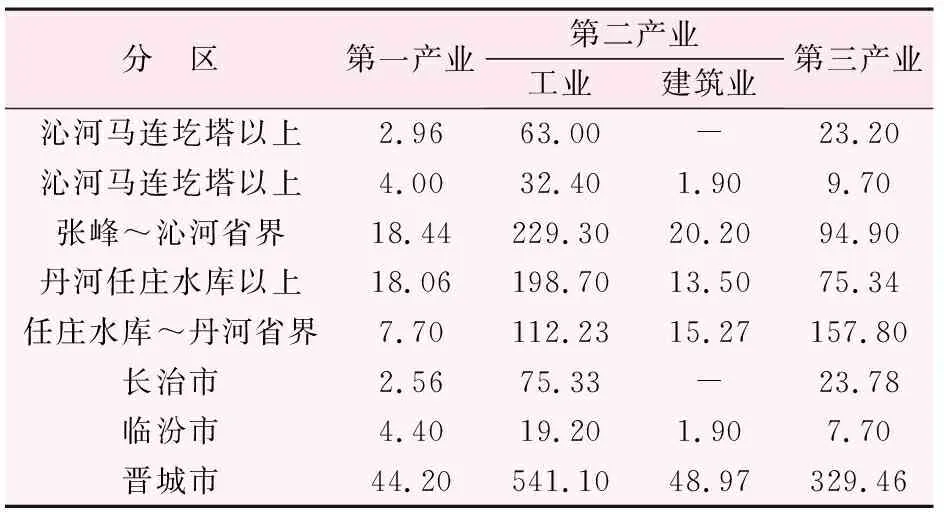
表4 沁河流域產業分布表

2 仿真實驗與結果分析

為驗證基于SHAW模型的山西沁河流域水資源配置方法的應用效果，采用仿真實驗加以驗證。

2.1 實驗準備

實驗在MATLAB仿真平臺中完成。選用沁河流經晉城市內的書院河作為實驗對象。書院河道總長為4.61 km，流域面積5.95 km2，平均縱坡26.8‰。書院河的地理位置如圖1所示。

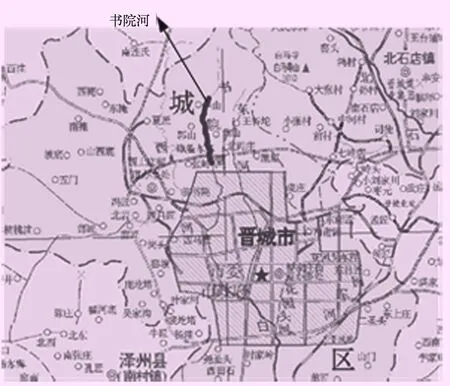
圖1 實驗流域對象地理位置圖

在此基礎上，結合書院河流域周圍的產業分布及人口分布，設定不同降水保證率下工業、農業及生活用水情況，結果如表5所示。

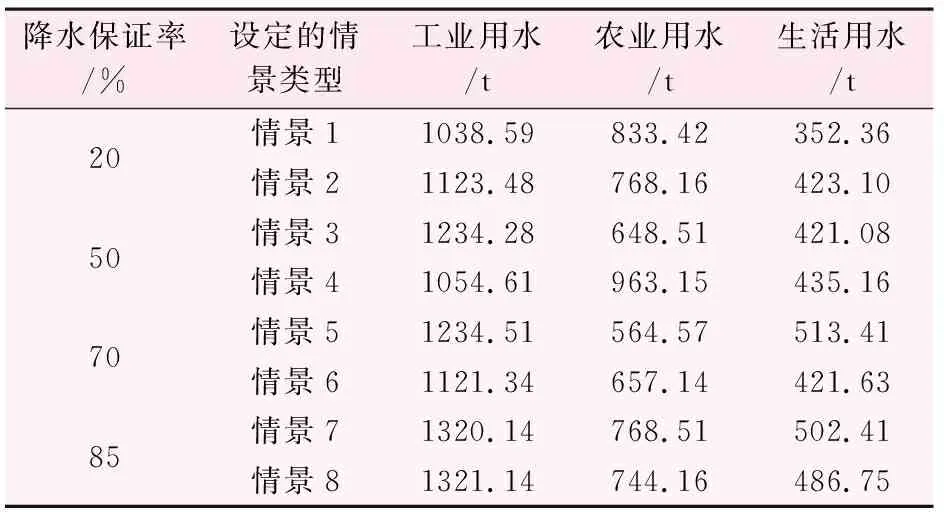
表5 實驗設定的水資源使用情景表

按照表5所示的設定情景，分別采用傳統的基于改進果蠅算法、基于地下水“雙控”與基于SHAW模型的水資源配置方法完成水資源模擬配置，并對比3種配置方法的應用性能。

2.2 實驗結果及分析

根據上述實驗準備，以配水量為計算指標，定義水資源的供需平衡系數計算公式如下：

(15)

式中：ε為供需平衡系數；Q為設定情景內的需水量；Q′為配備方法配置水量。一般來說，ε的數值越接近于1，則表示水資源配置方法的配比結果更佳。

匯總3種水資源配置方法的供需平衡系數，結果如表6所示。

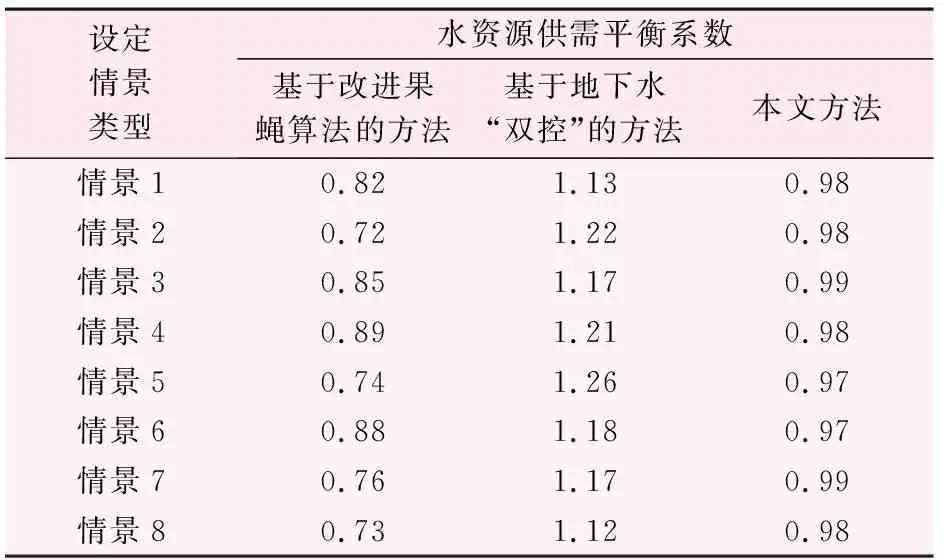
表6 三種配備方法供需結果表

由表6所示的供需平衡系數可知，基于改進果蠅算法的方法得到的供需平衡系數小于1，表明該方法并超出書院河所有產業的用水需求的預期，配置的水量過多，存在水資源浪費的情況，不利于流域內的水資源循環。基于地下水“雙控”的方法得到的供需平衡系數在1.20上下，大于1，表明該方法所配置的水量無法滿足該支流下產業的日常運營，不適合在沁河流域中使用。而應用基于SHAW模型的水資源配置方法得到的供需平衡系數接近1，表明該方法能夠在滿足產業的日常用水需求外，有效避免了配置的水資源過量。

綜上所述，基于SHAW模型的水資源配置方法更加適合在沁水流域水資源配置中應用，符合水資源供需平衡的實際需求。

3 結 語

隨著流域水資源與社會用水供需矛盾的日趨激化，對水資源進行合理分配成為了相關領域的研究熱點。本研究在SHAW模型的基礎上，實現了對山西沁河流域水資源的合理配置，有效減少了配置過程中水資源的浪費。