BDS-3精密單點定位性能比較分析

王利軍 焦文海 賈小林 曾 添 張 亮

1 長安大學地質工程與測繪學院，西安市雁塔路126號，710054 2 北京跟蹤與通信技術研究所，北京市北清路26號，100094 3 西安測繪研究所，西安市雁塔路中段1號，710054 4 信息工程大學地理空間信息學院，鄭州市科學大道62號，450001

對于日漸完善的北斗系統，其定位精度和空間幾何分布受到國內外學者的極大關注。但是，現階段還未有學者針對BDS-3的B1I-B3I、B1C-B2a兩種雙頻組合的PPP精度進行比較。本文利用MGEX觀測站數據，對BDS-3精密單點定位的非差非組合模型與無電離層組合模型定位性能進行對比分析。

1 基于衛星端DCB的精密鐘差改正模型

衛星信號從衛星內部產生到離開衛星發射天線的時間稱為衛星內部時延，2個不同頻率的信號或同一頻率不同測距碼之間的時延差是不同的。直接測定信號內部時延較為困難，所以一般采用2個信號的時延之差來處理。BDS衛星端差分碼偏差可達20 ns，對于cm級別的精密單點定位影響很大；接收機端差分碼偏差可被吸收到接收機鐘差內一起計算。

1.1 BDS衛星端DCB改正模型

目前共有3家分析中心發布BDS-3精密軌道和鐘差產品，分別是德國地學研究中心產品(GBM)、武漢大學產品(WUM)和西安測繪研究所產品(XRI)，三者都是基于B1、B3頻點無電離層組合解算得到的，因此使用不同頻點組合進行精密單點定位，其對應的DCB改正模型不同。B1I和B3I組成無電離層組合的方程為：

(1)

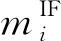
(2)

由此看出，當利用B1I、B3I頻點無電離層組合定位時，不需要進行DCB改正。當采用B1C和B2a組合時，其衛星鐘差參數可表示為：

(3)

將其歸算到B1I和B3I組合基準下，即將式(2)代入式(3)，可得：

(4)

在DCB產品中，各參數定義為：

(5)

進行等式代換后可得：

(6)

1.2 北斗三號DCB穩定性分析

由上文可知，北斗三號DCB產品的質量將直接影響B1C-B2a雙頻組合PPP的定位精度，因此對上述DCB產品中的3個參數的穩定性進行分析。現階段共有2種支持BDS的DCB產品[1]，一種是由德國宇航中心(DLR)利用全球MGEX站計算的高精度電離層模型(GIM)修正衛星信號在傳播路徑上的電離層延遲，從而計算出衛星和接收機的差分碼偏差[2-4]；另一種是中國科學院利用觀測站數據建立電離層TEC模型并解算衛星以及接收機的差分碼偏差[5-6]。自2019-11開始，中國科學院發布的DCB產品支持MGEX和iGMAS的B1C、B2a頻點的觀測數據。實驗數據選取2020-05-17～06-15(doy 138～167)中國科學院發布的碼偏差產品，圖1、2、3分別為DCBC1X-C5X、DCBC1X-C6I、DCBC2I-C6I的日解值，其中DCBC1X-C5X代表B1C和B2a之間的頻間偏差，DCBC1X-C6I代表B1C和B3I之間的頻間偏差，DCBC2I-C6I代表B1I和B3I之間的頻間偏差。表1給出了BDS-3衛星3個碼偏差產品的標準差和均值。

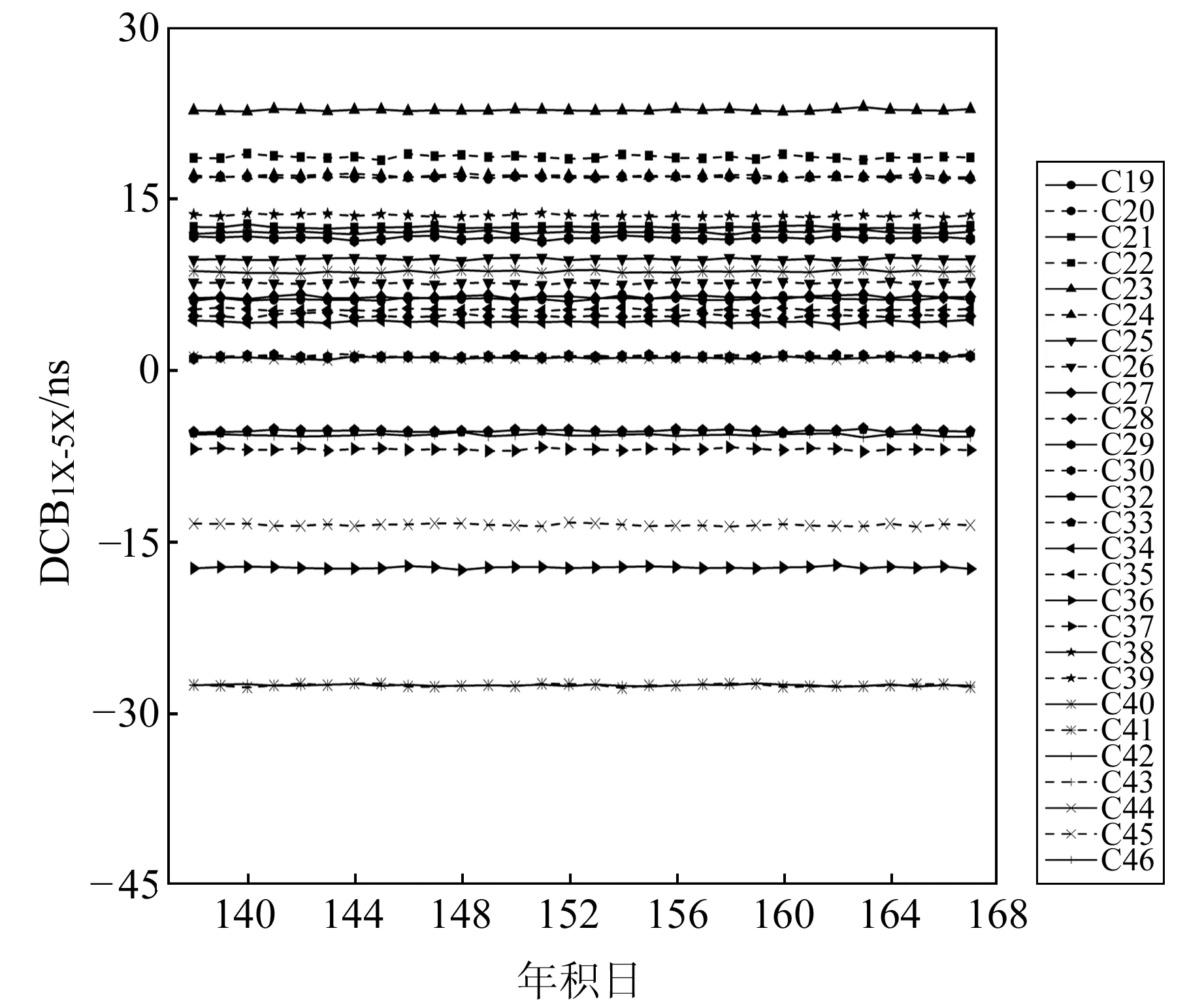
圖1 BDS-3衛星DCBC1X-C5X值Fig.1 The values of BDS-3 DCBC1X-C5X

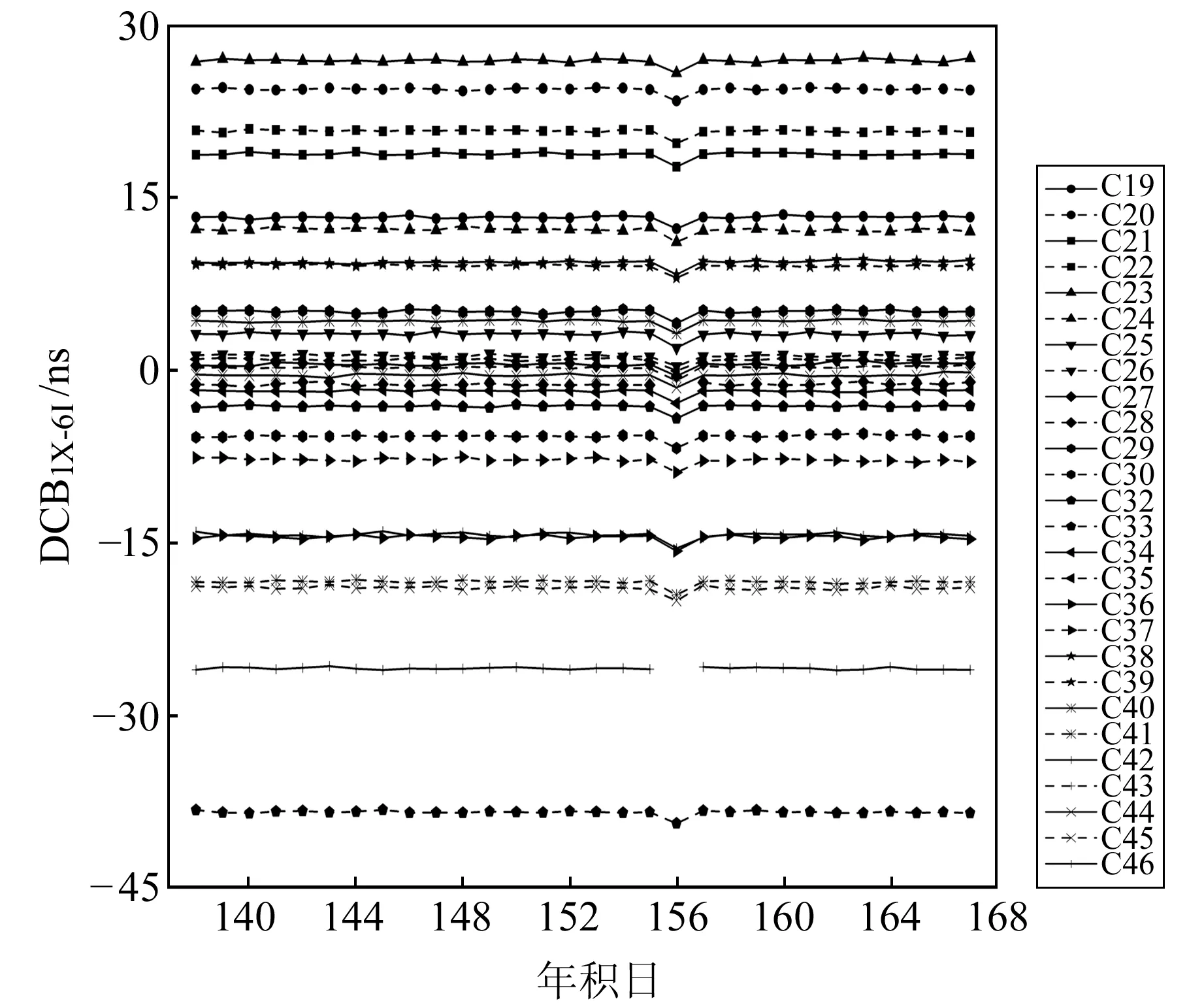
圖2 BDS-3衛星DCBC1X-C6I值Fig.2 The values of BDS-3 DCBC1X-C6I

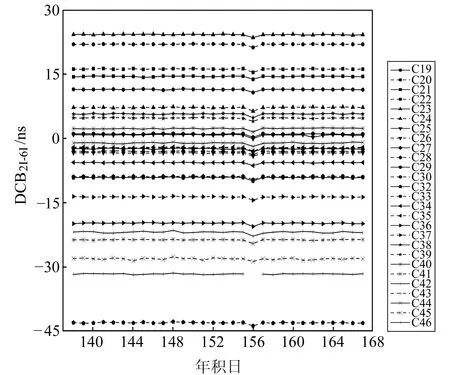
圖3 BDS-3衛星DCBC2I-C6I值Fig.3 The values of BDS-3 DCBC2I-C6I

由圖2、3可以看出，C42衛星在doy 156的DCBC1X-C6I、DCBC2I-C6I值缺失，導致當天其他BDS-3衛星的DCB值發生明顯波動，這可能是因為用于解算DCB的觀測值中缺少C42衛星B3I頻點的觀測數據[7]。除此之外，3種DCB值在1個月內變化較為平穩，基本都在0.5 ns范圍內波動。由表1可以看出，DCBC1X-C5X的范圍在-28～23 ns之間，其標準差都在0.100 ns左右；DCBC1X-C6I、DCBC2I-C6I的范圍在-45～30 ns之間，平均標準差分別為0.210 ns、0.158 ns。由此可見，DCBC1X-C5X的穩定度優于DCBC2I-C6I、DCBC1X-C6I。

2 算例分析

為了評估BDS-3精密單點定位不同模型的定位性能，分別進行靜態和模擬動態實驗，從定位精度和收斂時間2個方面對比非差非組合和無電離層組合模型下的B1I-B3I、B1C-B2a雙頻組合的PPP定位性能。選取2020-05-30～06-05(doy 151～157)MGEX觀測網中GCGO、UNB3、RGDG、NYA2、BRST、SUTM、SGOC、KRGG、ULAB、WUH2等10個測站的實測數據進行實驗。由于北斗三號的GEO衛星不播發B1C和B2a信號，因此將其剔除，只選取C19～C46衛星參與計算。實驗真實坐標來源于IGS提供的站坐標天解文件，表2給出PPP處理策略。

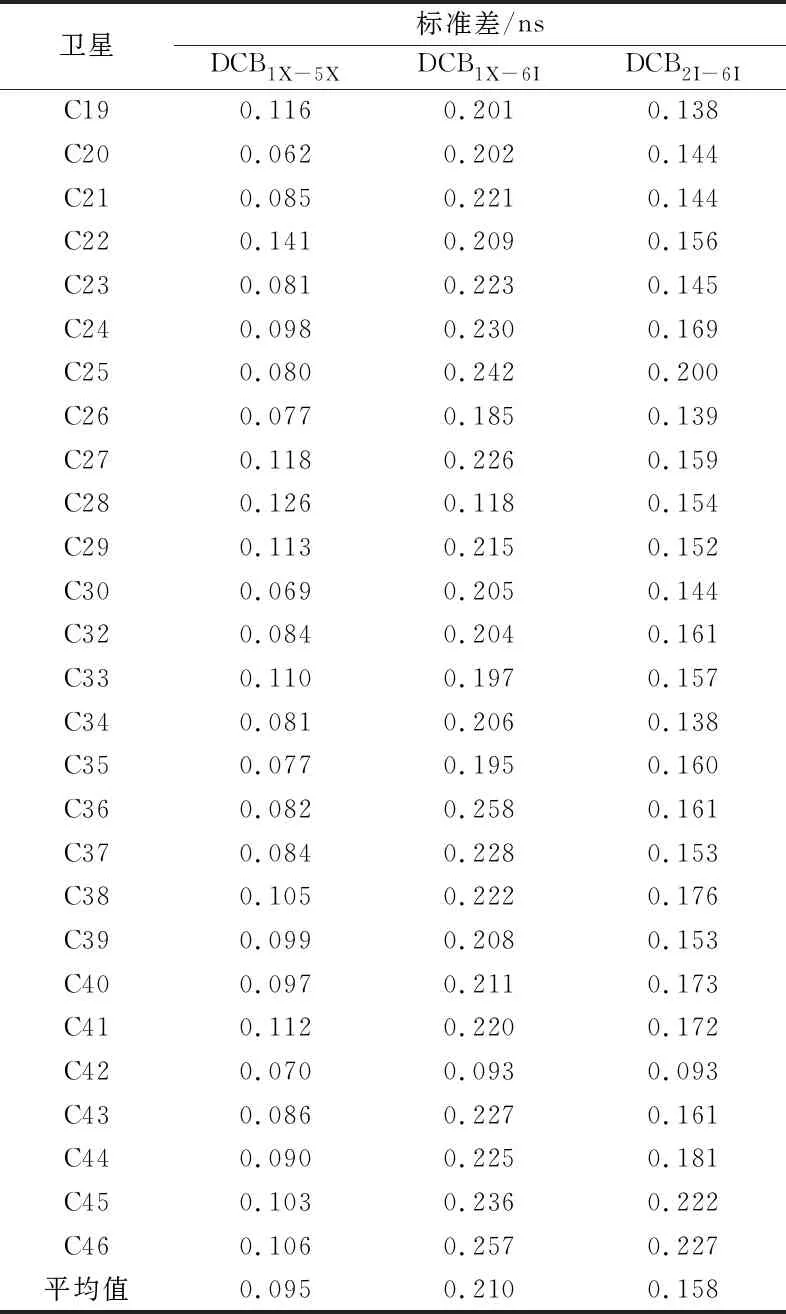
表1 BDS-3衛星DCB產品的標準差

表2 精密單點定位處理策略

2.1 靜態定位精度分析

圖4給出了10個測站6種模型連續7 d的單天靜態解在E、N、U方向的RMS的平均值，其中IF-BDS-2/3和UC-BDS-2/3分別表示BDS-2+BDS-3的B1I-B3I雙頻組合的無電離層組合和非差非組合模型。表3統計了所有測站連續7 d的單天靜態解在E、N、U和三維方向的RMS的平均值。由圖4和表3可以看出，各個模型的靜態RMS在E方向上都優于1.8 cm，N方向優于1.1 cm，U方向優于2.5 cm，三維方向優于3.3 cm。對表3中BDS-3的不同雙頻組合的無電離層和非差非組合模型的E、N、U方向定位精度取平均值，可以得出無電離層組合模型平均定位精度分別為1.7 cm、0.9 cm、2.1 cm，非差非組合模型的分別為1.73 cm、0.9 cm、2.2 cm，二者靜態定位精度基本一致。對于不同定位模型的2種雙頻組合，B1C-B2a雙頻組合的平均定位精度分別為1.65 cm、1.1 cm、1.7 cm，B1I-B3I雙頻組合的則分別為1.8 cm、0.8 cm、2.4 cm，可見B1C-B2a、B1I-B3I雙頻組合靜態定位精度基本相當。BDS-2是區域衛星導航系統，服務范圍在55°S～55°N、70°E～150°E，本文實驗中WUH2和SGOC測站在其范圍內。比較2個測站BDS-3和BDS-2/3定位的精度可以得出，BDS-2/3較BDS-3在三維方向上精度平均提升9.4%。

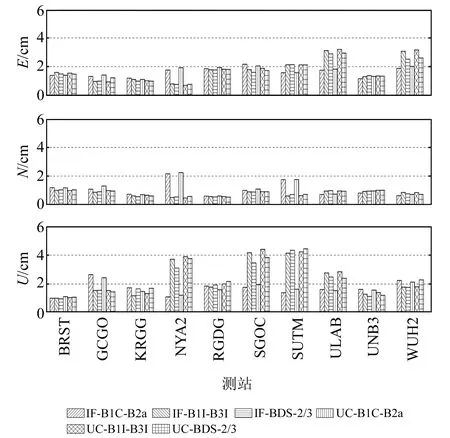
圖4 6種PPP模型10個測站單天靜態定位平均RMSFig.4 Average of RMS for 10 stations of 6 PPP models in daily static solutions

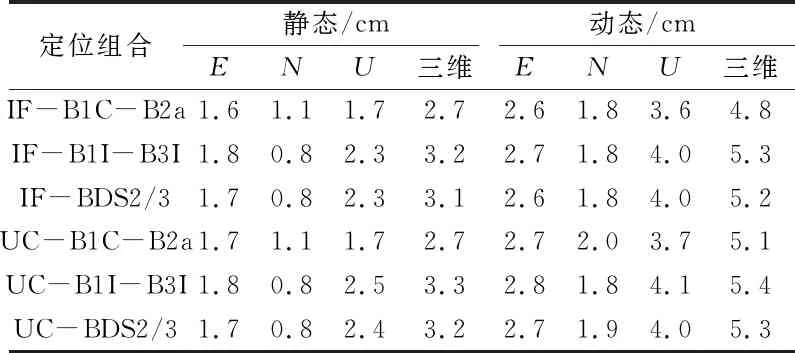
表3 6種PPP模型單天靜態和模擬動態定位平均RMS

2.2 模擬動態定位精度分析

采用與靜態實驗相同的處理策略進行模擬動態實驗。圖5給出了10個測站6種模型連續7 d的單天動態解在E、N、U方向的RMS的平均值。由圖5和表3可以看出，10個測站6種模型的RMS在E、N、U方向上分別優于2.8 cm、2.0 cm、4.1 cm，三維方向優于5.4 cm。模擬動態的無電離層組合在3個方向的平均定位精度分別為2.63 cm、1.8 cm、3.87 cm，非差非組合的分別為2.73 cm、1.9 cm、3.93 cm，二者動態定位精度相當。雙頻組合方面，B1C-B2a雙頻組合在3個方向的平均定位精度分別為2.65 cm、1.9 cm、3.65 cm，B1I-B3I雙頻組合的分別為2.75 cm、1.8 cm、4.05 cm，可見2種雙頻組合動態定位精度基本一致。對WUH2和SGOC測站而言，BDS-2/3較BDS-3在三維方向上精度平均提升13.1%。

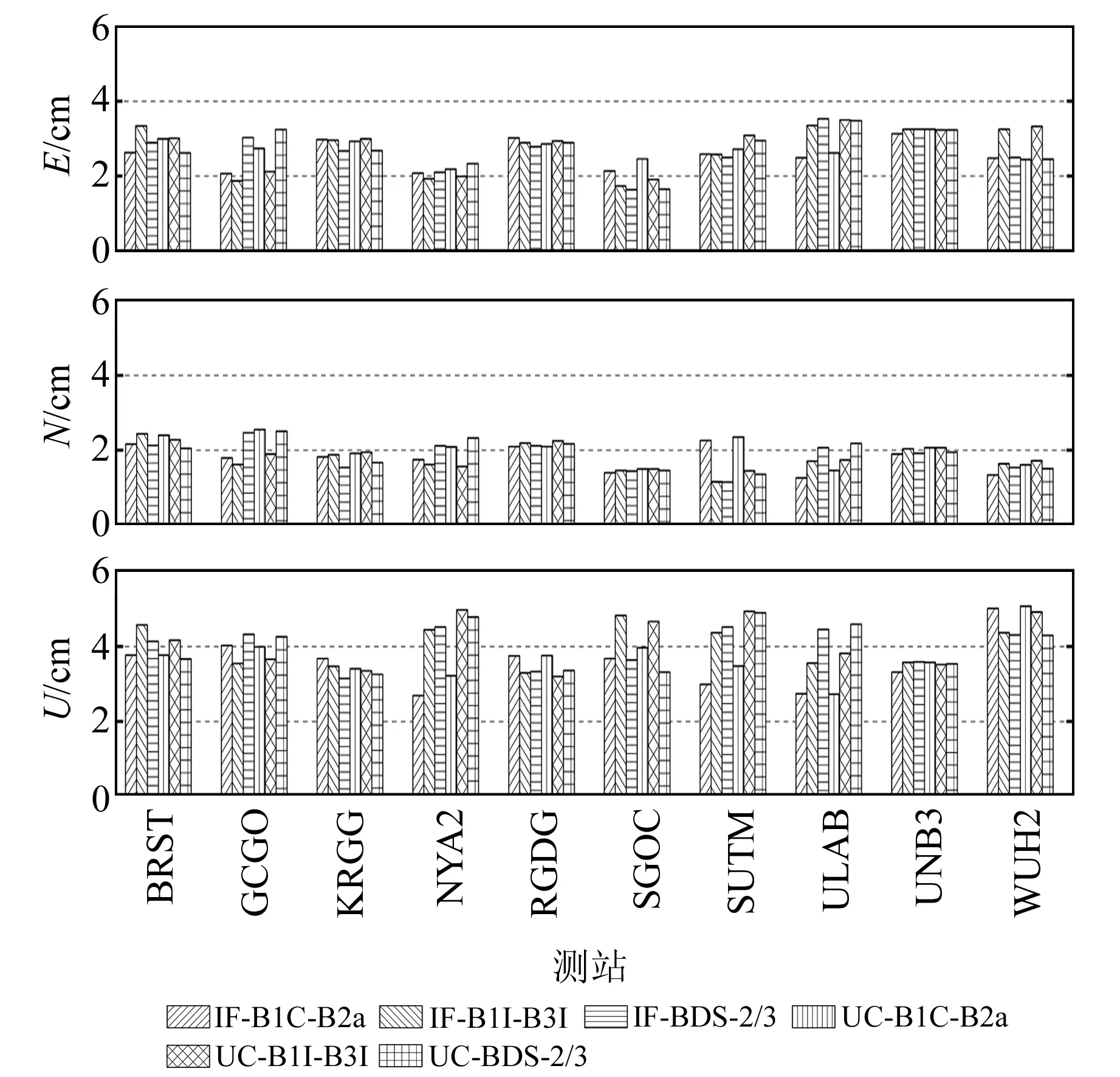
圖5 6種PPP模型10個測站單天模擬動態定位平均RMSFig.5 Average of RMS for 10 stations of 6 PPP models in daily kinematic solutions

2.3 收斂性分析

為了分析不同雙頻組合和不同定位模型的收斂時間，對上述10個測站連續7 d的觀測數據進行靜態和模擬動態PPP計算，并統計各測站E、N、U分量定位誤差連續20個歷元均小于1 dm所需要的時間。圖6給出了各個測站連續7 d靜態和模擬動態定位收斂時間的平均值，表4統計了所有測站連續7 d靜態和模擬動態定位收斂時間的平均值。

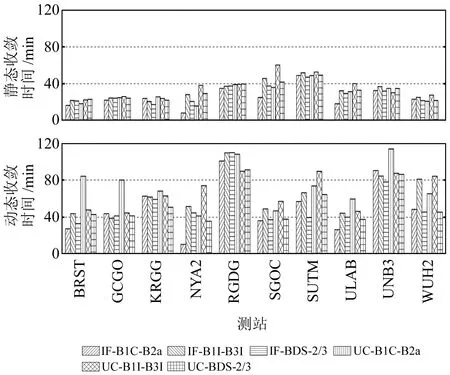
圖6 6種PPP模型10個測站單天靜態和模擬動態平均收斂時間Fig.6 Average convergence time of 6 PPP models for 10 stations in daily static and kinematic solutions

由圖6可以看出，10個測站靜態定位收斂時間基本都在50 min以內，動態定位收斂時間基本在90 min以內。對表4中各種模型定位收斂時間取平均值，可以得到BDS-3靜態定位平均收斂時間在31 min左右，動態定位則在60 min左右。靜態定位中在無電離層組合和非差非組合模型下的B1C-B2a雙頻組合較B1I-B3I收斂時間平均減少7 min左右，動態定位平均減少13 min左右。在B1C-B2a、B1I-B3I雙頻組合下，無電離層組合模型靜態和動態的平均收斂時間分別為約29 min、57 min，非差非組合模型的則分別為約33 min、62 min，由此可以看出，無電離層組合與非差非組合模型收斂時間基本一致。WUH2和SGOC站的BDS-2/3靜態收斂時間較BDS-3平均提升22.8%，動態收斂時間平均提高38.7%。

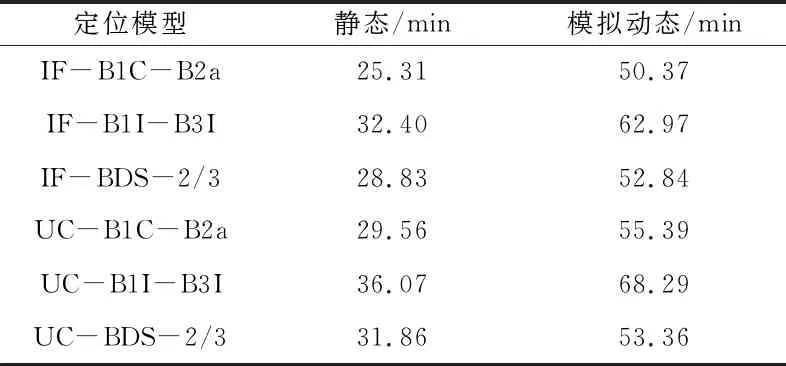
表4 6種PPP模型靜態和模擬動態定位平均收斂時間

3 結 語

本文推導出BDS-3新頻點B1C-B2a組合衛星端DCB改正模型，同時利用全球分布的10個MGEX站7 d的觀測數據以及西安測繪研究所發布的精密軌道鐘差產品，進行不同定位模型和不同雙頻組合的靜態和模擬動態PPP實驗，并分析各個模型的定位精度和收斂時間。結果顯示，BDS-3靜態精密單點定位在水平方向的RMS優于2.0 cm，高程方向優于2.5 cm，平均收斂時間在31 min左右。模擬動態定位的水平方向RMS優于3.4 cm，高程方向優于4.1 cm，平均收斂時間在60 min左右。對于亞太地區的2個測站，靜態定位中，BDS-2/3較BDS-3在三維方向上精度平均提升9.4%，收斂時間平均提升22.8%；動態定位中，三維方向上精度平均提升13.1%，收斂時間平均提升38.7%。

由于全球范圍內可以同時觀測BDS-3四個頻點的觀測站較少，本文僅采用10個全球分布的MGEX站進行研究。通過本文實驗結果看到，B1I-B3I和B1C-B2a雙頻組合的定位精度相當，收斂時間較為接近，且二者均適用于北斗精密單點定位。隨著精密軌道和鐘差產品精度的提高以及其他精密產品的完善，BDS-3全球精密單點定位性能將會進一步提升。